开孔变截面微悬臂梁传感器的等效刚度和固有频率*

陈金龙,吴君正,张能辉,2*

(1.上海大学上海市应用数学和力学研究所,上海市力学在能源工程中的应用重点实验室,上海 200072;2.上海大学理学院力学系,上海 200444)

开孔变截面微悬臂梁传感器的等效刚度和固有频率*

陈金龙1,吴君正1,张能辉1,2*

(1.上海大学上海市应用数学和力学研究所,上海市力学在能源工程中的应用重点实验室,上海 200072;2.上海大学理学院力学系,上海 200444)

研究新型开孔变截面微悬臂梁传感器的等效法向刚度及其对固有频率的影响。首先,考虑微梁纵截面孔洞结构引起的弯扭耦合效应,利用二次积分法获得在自由端集中载荷作用下悬臂梁的挠度,基于弹性材料的Hooke定律建立了微梁等效法向刚度分析的解析模型。然后,采用Rayleigh法获得了微梁的固有频率。最后,通过比对实验结果和有限元结果对解析模型进行了验证。研究表明:解析模型对于开孔变截面微梁刚度和频率的预测和标定具有较好的精度;微梁的等效刚度和固有频率与跨宽比负相关,却与内外宽度比正相关。有关结论可为新型变截面微纳机械传感器的设计提供理论依据和参考。

微悬臂梁传感器;变截面;等效刚度;固有频率;解析方法

微梁传感器领域起步于20世纪90年代中期,吸引了大量学者的关注。由于具有无标记、高灵敏、轻便、廉价、高度并行、快速传感和通用化等优点,微梁传感器在生命科学、医学、环境监测、食品工程和军事等领域有着广泛的应用前景[1]。韩国Eom[2]、丹麦Boisen[3]、西班牙Tamayo[4-5]和美国Roukes[6]等国外课题组在等截面微梁传感器领域已开展了较为突出的探索,但大多集中在测试技术原理的实验展示方面,实验数据的发散性和表界面问题的跨尺度特性给问题的定量化表征带来许多挑战,阻碍了这一高新技术的市场化步骤。

国内在实验研究方面,伍小平、张青川和李凯等利用微梁传感器对两种中药成分(青蒿素和马兜铃酸)抗原抗体的特异性结合进行检测,能测得极低浓度的样品,显示了微梁传感技术对中药成分检测的可行性[7];李昕欣等提出了一种基于平面内谐振模态和电热驱动的新型微悬臂梁检测模式,相比传统的面外谐振微悬臂梁,能够有效地降低微悬臂梁在液体中拖拽力,减少能量损失和获得高的品质因子,并测试比较了在水中和空气中谐振特性[8];童朝阳等探索了压阻式微悬臂梁传感器在生化毒剂检测方面的应用[9]。在理论研究方面,赵亚溥等将表面弹性引入具有残余应力的纳米板结构中,发现表面效应的影响体现在对应经典Kirchhoff板理论中控制方程系数的变动,由此研究了纳米板尺寸依赖的自屈曲和弯曲行为[10];冯西桥和王刚峰等通过建立具有“三明治”结构的欧拉梁和铁摩辛柯梁模型,阐述了表面弹性、表面残余应力和剪切变形等对微梁轴力和固有频率的影响[11];段慧玲和王建祥等研究了表面粗糙度对表面应力的影响、以及常表面应力和应变相关表面应力对微梁动态频率的影响[12];张能辉等利用DNA液晶理论、聚电解质溶液电势理论和连续介质力学等建模方法,建立了DNA-微梁纳米力学分析的四层梁跨尺度能量模型,研究了微梁生物传感器制备和检测过程中的随机性效应、杂交放热效应、压电效应和吸附膜宏观弹性模量等[13-16]。

为了提高检测灵敏度和抗干扰能力,国内外学者开始探索研究具有变截面梁的传感器。Ece等研究了边界约束条件和横截面变化对微梁频率和模态的影响,发现频率变化对梁宽的变化不敏感,而振幅变化却显著依赖于梁宽的变化[17];Thundat等研究了分子吸附对变截面微悬臂梁表面应力和固有频率的影响,指出固有频率的变化是由吸附质量变化与弹簧常数变化共同引起的,而同时测量微梁变形和固有频率变化可以解耦质量变化和弹簧常数变化的影响[18];Raman等采用Anderson局部振动方法,发现振幅变化是频率变化的几个数量级,并具有内部共模抑制特性,指出检测振幅变化可获得更高的检测灵敏度[19];Morshed和Prorok利用有限元分析了微梁几何形状对检测灵敏度的影响,发现自由端的有效质量和固定端的宽度起主导作用,建议采用三角形微悬臂梁,因为三角形梁比矩形梁的灵敏度高一个数量级[20];而姚军等限元结果表明,微梁外形对静态检测灵敏度没有影响,但对动态检测灵敏度影响较大,而且三角形梁的灵敏度最高[21];Cho等提出了一种具有复杂几何外形的变截面耦合双梁,采用多尺度分析方法研究了耦合元件几何非线性和尺寸变化对微梁幅频响应的影响[22],但并未给出集总参数模型所需等效刚度的理论模型,而仅是通过拟合幅频响应实验曲线获得微梁的等效刚度。

在精确测量生物分子或化学分子之前,必须对微梁的刚度进行标定。目前实验中常用的刚度标定方法有两种,一是增加质量法[23],通过将已知质量添加到微悬臂的自由端测量基本振动模式下共振频率的变化;二是无负载共振技术[24],需要测量无负载振动的共振频率、基本振动模态的品质因子和微梁的几何尺寸[25]。这些实验方法均涉及微梁固有频率的检测,而表面涂层、阻尼和负载点位置等都会对检测结果产生较大影响[26]。因此,不可避免的实验误差使理论研究显得非常必要,Sader采用水动力函数法(hydrodynamic function)预测了几种特定几何形状变截面梁的刚度与其几何尺寸、材料常数的关系,但其解析模型不适用于小长宽比的复杂变截面微梁的设计[27]。

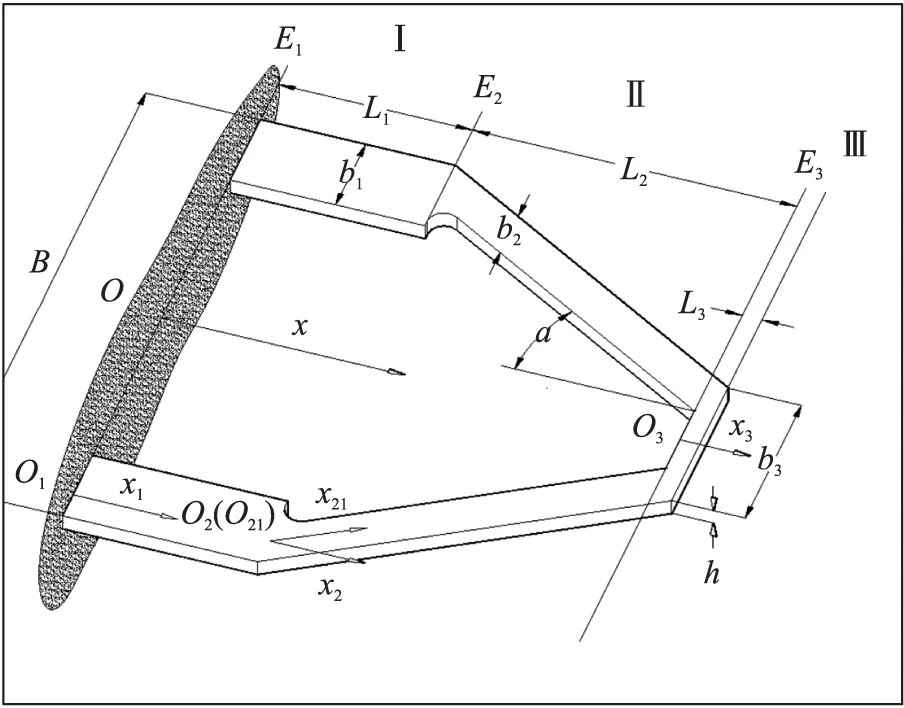
图1 变截面微悬臂梁的几何示意图

本文致力于研究更为复杂变截面微梁的等效法向刚度及其对微梁固有频率的影响。首先,针对如图1所示耦合双梁实验中具有复杂几何外形的变截面外梁[22],在自由端集中载荷作用下,考虑纵截面孔洞结构引起的弯扭耦合效应,仿照Neumeister-Ducker方法(以下简称ND方法)[28],采用二次积分法获得了变截面微梁的挠度,并基于弹性材料Hooke定律建立了微梁等效法向刚度的解析新模型。然后,采用静态挠度近似代替振型函数,结合Rayleigh法和上述等效法向刚度新模型预测了微梁的固有频率。最后,采用Cho的实验结果[22]和本文有限元数值结果验证了解析新模型的可靠性,并讨论了几何尺寸对微梁等效刚度和固有频率的影响。

1 数学模型

图1为Cho耦合双梁实验中变截面外梁的几何示意图[22],微梁的厚度为h,分为Ⅰ、Ⅱ、Ⅲ3段,长度分别为L1,L2,L3,内部宽度分别为b1,b2,b3,外部宽度为B。如图建立整体坐标系的x轴和局部坐标系的x1,x2,x21,x3轴,三段的挠度分别为w1(x1),w2(x2)或w21(x21),w3(x3),对应的转角分别为θ1(x1),θ2(x2),θ3(x3)。为求解微梁的等效法向刚度,假设集中载荷N作用在微梁的自由端。需要指出,由于纵向截面的孔洞结构特征,微梁侧臂的变形属于弯扭组合变形,经典Euler梁理论已不再适用。这里将仿照ND方法[28],考虑扭转效应给微梁侧臂带来的附加挠度。

1.1 微梁的挠度

微梁Ⅰ段的变形为弯扭组合变形,但由于Ⅰ段与x轴平行,扭转效应对Ⅰ段侧臂轴线的挠度并没有贡献,于是采用二次积分法获得微梁Ⅰ段的挠度为

(1)

这里Ⅰ段的抗弯刚度I1=b1h3/12,弯矩M(x1)=F1(L1-x1)+M1,其中F1=N/2,M1=N(L3+L2)/2,再由固定端边界条件x1=0,w1=0,w1x=0可得

(2)

于是Ⅰ段与Ⅱ段交界点E1处的挠度和转角分别为

wE1=w1(L1),θE1=θ1(L1)

(3)

微梁Ⅱ段的变形为弯扭组合变形,由于Ⅱ段与x轴有夹角α,需要考虑扭转效应对Ⅱ段侧臂轴线挠度的贡献,于是采用积分法和ND方法获得微梁Ⅱ段的挠度为

(4)

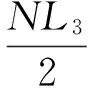
(5)

由于x21为沿Ⅱ段轴线方向的局部坐标,所以

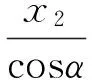
(6)

于是Ⅱ段与Ⅲ段交界点E2处的挠度和转角分别为

wE2=wE1+θE1L2+w2(L2),θE2=θE1+θ2(L2)

(7)

微梁Ⅲ段的变形为纯弯曲变形,采用二次积分法获得微梁Ⅲ段的挠度为

(8)

式中

M(x3)=N(L3-x3),I(x3)=[b3+2(L3-x3)tanα]h3/12

(9)

式中

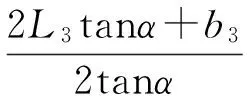
log[2tanα(L3-x3)+b3]

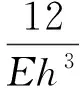
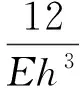
(10)

其中局部坐标与全局坐标之间的关系为

x1=x,x2=x-L1,x3=x-L1-L2,x21=x2/cosα

(11)

则微梁的自由端挠度为

wE3=wE2+θE2L3+w3(L3)

(12)

1.2 微梁的等效法向刚度、等效质量和固有频率

由式(12)获得微梁自由端挠度wE3后,根据弹性材料的Hooke定律,微梁的等效法向刚度可由式(13)获得

K=N/wE3

(13)

下面将给出微梁等效质量Me的近似解析解。假设梁的弯曲挠度w(x)可以采用下列单一模态振动近似[29]

w(x,t)≈Φi(x)qi(t)

(14)

式中:Φi(x)为归一化的特征振型函数,qi(t)为自由端E2处的挠度。采用Rayleigh法[30],不妨将以上获得的微梁静挠度曲线(即式(10))作为近似振型函数,即

Φi(x)=w(x)/wE3

(15)

于是微梁的动能为

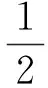
(16)

式中:S(x)表示梁的横截面面积,而且

S1(x1) =2b1h,S2(x2)=2b2h,

S3(x3)=[2(L3-x3)tanα+b3]h≈(b3+L3tanα)h

于是,利用式(16)可得微梁的等效质量为

(17)

利用(13)和(17)获得等效刚度和等效质量后,可由式(18)获得微梁的固有频率为

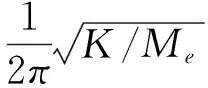
(18)

2 结果与讨论

以上建立了利用微梁几何参数和材料参数预测变截面微梁等效方向刚度及其一阶模态固有频率的解析表达式,下面将利用有限元方法和有关实验数据验证其可靠性,并研究几何尺寸变化对微梁等效刚度和固有频率的影响。

2.1 解析解与有限元解以及实验结果的比对

Cho实验中[22]微梁的几何尺寸L1=60 μm,L2=100 μm,L3=6 μm,B=178 μm,b1=27 μm,b2=16 μm,b3=51 μm,h=2.1 μm,α=31°,材料参数E=187 GPa,ν=0.27,ρ=2.33 g/cm3。有限元分析时采用了Ansys软件的Tetrahedron单元,单元数1 083,经收敛性分析已经满足计算精度需要。

表1给出了微梁刚度的解析预测、有限元离散解以及微梁一阶模态固有频率的实验观测值、解析预测值和有限元离散解。因为缺乏微梁刚度的实验观测值,这里仅给出了基于上述刚度公式(13)的解析预测值与有限元离散解进行了比对。从表1中可以看出,有关微梁刚度的解析预测值与有限元结果十分接近,而基于前述频率公式(18)的解析预测值与实验值误差仅为5.77%,而有限元解与实验值的误差为7.72%,不过解析预测值与有限元解的误差仅有2%。考虑到实验环境、操作方法和测量精度等因素的影响,可以看出本文解析预测值与实验数据吻合良好,这在一定程度上验证了本文解析模型的可靠性。需要指出的是,以上算例中微梁的纵向截面具有孔洞结构,而Sader等有关解析模型[27]仅适用于纵向截面没有开孔的情形,可见本文考虑弯扭耦合效应的解析模型填补了这方面的不足。

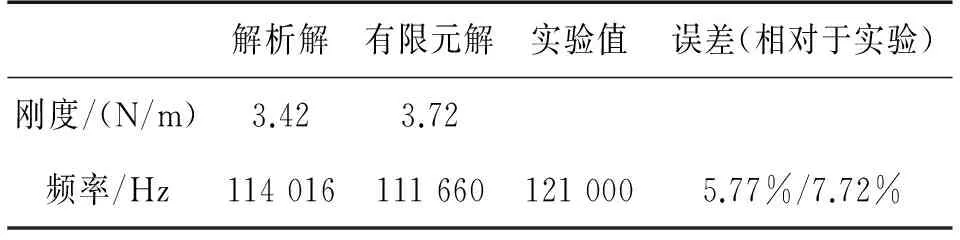
表1 变截面微梁刚度、固有频率的理论预测与实验值[22]的比对

2.2几何尺寸变化对变截面微梁等效法向刚度和固有频率的影响

为更好地应用和检验本文解析模型(即式(13)和式(18)),以下将研究几何尺寸变化对微梁等效刚度和固有频率的影响,为便于研究,这里取b1=b2。

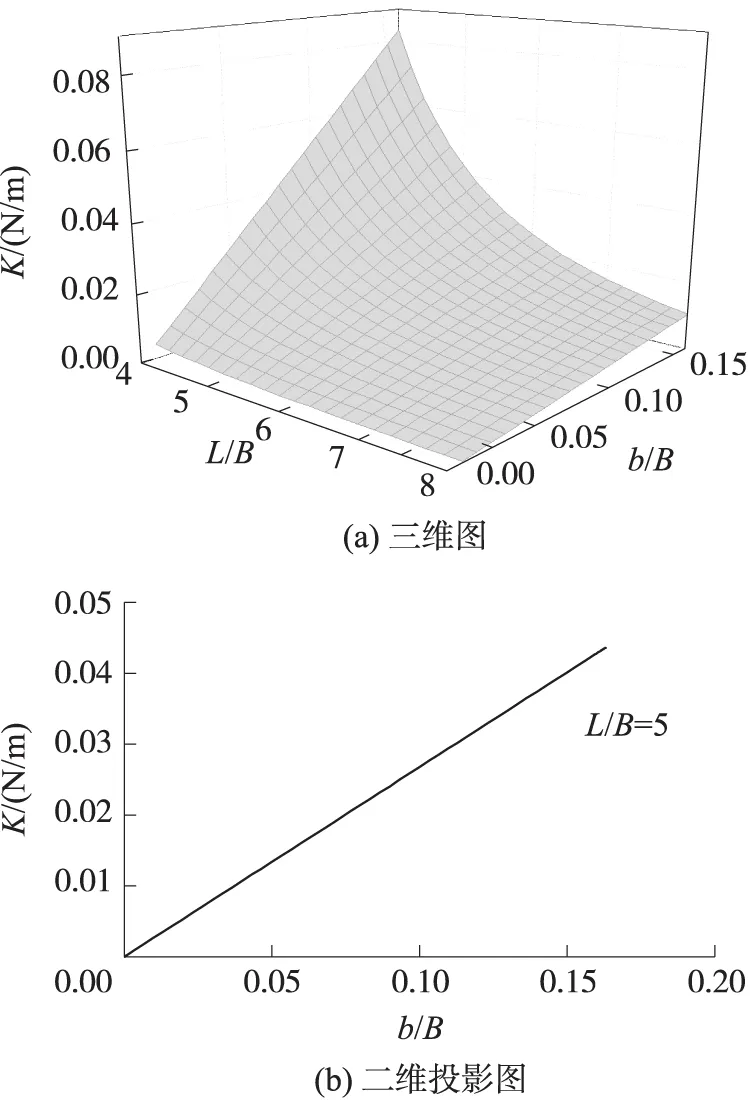
图2 几何尺寸变化对变截面微梁法向刚度的影响

图2给出了变截面微梁等效刚度随跨宽比L/B和内外宽度比b/B的变化趋势,图2(a)是三维图,而图2(b)则给出了在L/B=5时微梁等效刚度随内外宽度比变化的二维图。从图2可以看出,随着跨宽比的增加,等效刚度逐渐减小;而随着内外宽度比的增加,等效刚度呈线性增加。众所周知,经典Euler细长梁理论中弯曲刚度与梁宽的一次方成比例,与梁厚的三次方成比例,显然,本文给出的变截面微梁等效刚度与内外宽度比的线性依赖性关系与经典Euler细长梁理论的结论非常相似。

图3给出了变截面微梁固有频率随跨宽比L/B和内外宽度比b/B的变化趋势,图3(a)是三维图,图3(b)则给出了在L/B=5时微梁固有频率随内外宽度比变化的二维图。由图3(a)和图3(b)可见,随着跨宽比的增加,固有频率逐渐减小;而随内外宽度比的增加,固有频率却呈现出非线性增长趋势。注意到,基于Euler梁理论,Ece等利用有限元方法研究了截面宽度变化对非开孔变截面梁动力特性的影响[17],发现非开孔变截面梁的频率与梁宽变化弱相关,显然,Ece等人的结论[17]不同于本文给出的开孔变截面微梁固有频率与内外宽度比的非线性依赖关系[17],主要原因是本文利用ND方法考虑了开孔结构特征引起的弯扭耦合效应[28]。

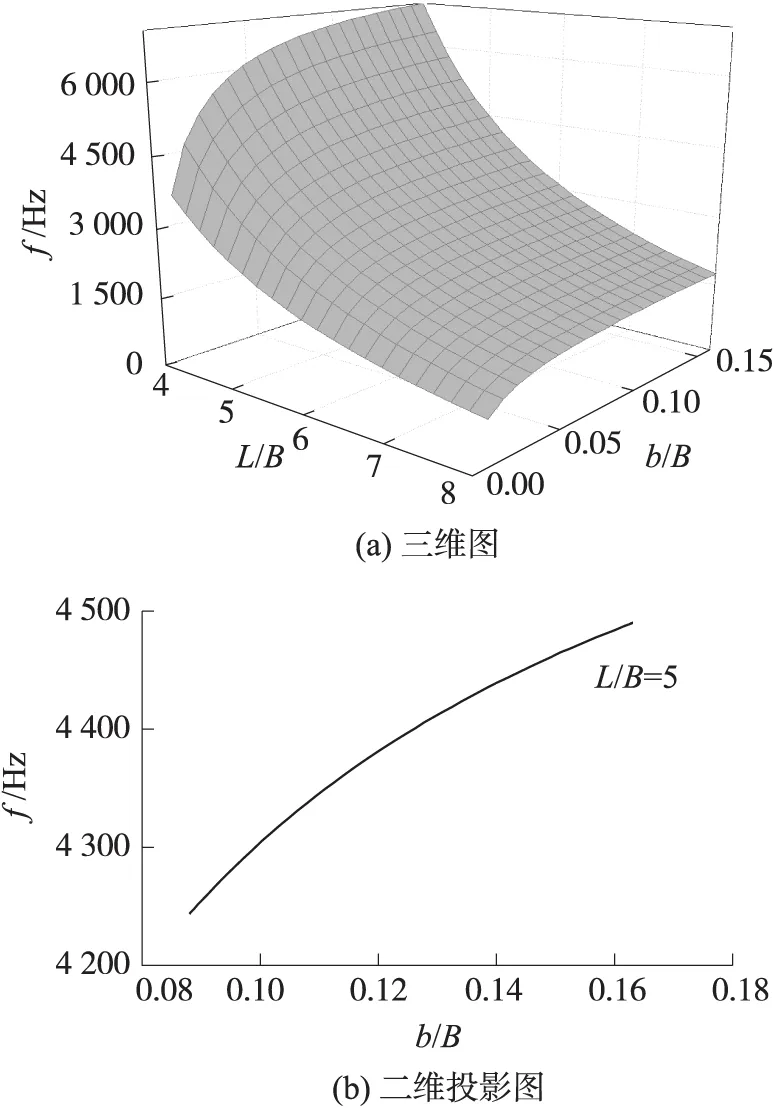
图3 几何尺寸变化对变截面微梁固有频率的影响

图4给出了变截面微梁刚度和频率的解析预测结果和有限元结果的比值随梁跨高比L/h的变化趋势,图中几何参数L/B=1.0,b/B=0.1。由图4(a)和图4(b)可见,随着跨高比的增加,本文一维解析模型给出的刚度和固有频率的预测值与三维有限元数值结果的误差均逐渐较小,且刚度比值km/k逐渐趋近于1,而频率比值fm/f逐渐趋近于0.98,显然本文解析预测的误差均落在工程允许误差5%以内。此外,比较图4(a)和图4(b)可以发现,当跨高比L/h>8时,频率比值已落在5%工程允许误差线内,但对于刚度比值,则需要跨高比L/h>15,才能落在5%工程允许误差线内。由以上分析可见,对于跨高比在15以上的变截面微梁,本文解析模型关于等效刚度和频率的预测可以达到足够的精度。

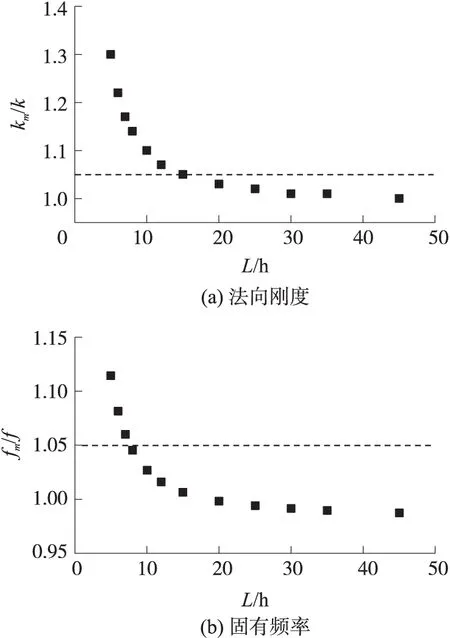
图4 变截面微梁法向刚度和固有频率的解析预测结果与有限元结果的比较

3 结论

考虑新型开孔变截面微梁的弯扭耦合效应,采用二次积分法和Rayleigh法,建立了预测复杂变截面微梁等效法向刚度和固有频率的解析模型,并比较了解析预测、有限元数值解和实验观测值之间的差别。研究表明:①当跨高比L/h>15时,本文提出的解析模型具有较高的精度,与有限元方法比,节省了计算成本,并克服了实验方法的局限性;对于跨高比L/h≤15的微梁,需要采用考虑剪切效应的有关粗短梁的理论进一步研究;②随着跨宽比L/B的增加,微梁的等效法向刚度和固有频率均逐渐减小;而随着内外宽度比b/B的增加,微梁的等效法向刚度呈线性增加,而固有频率却非线性增加,这明显不同于基于经典Euler梁理论关于未开孔变截面梁固有频率与梁宽弱相关性的认识。这些认识为新型开孔变截面微梁传感器的设计和刚度标定提供了参考。

[1] Zhang N H,Tan Z Q,Li J J,et al. Interactions of Single-Stranded DNA on Microcantilevers[J]. Current Opinion in Colloid and Interface Science,2011,16(6):592-596.

[2] Eom K,Park H S,Yoon D S,et al. Nanomechanical Resonators and Their Applications in Biological/Chemical Detection:Nanomechanics Principles[J]. Physics Reports,2011,503(4):115-163.

[3] Boisen A,Dohn S,Keller S S,et al. Cantilever-Like Micromechanical Sensors[J]. Reports on Progress in Physics,2011,74(3):036101.

[4] Calleja M,Kosaka P M,San Paulo,et al. Challenges for Nanomechanical Sensors in Biological Detection[J]. Nanoscale,2012,4(16):4925-4938.

[5] Tamayo J,Kosaka P M,Ruz J J,et al. Biosensors Based on Nanomechanical Systems[J]. Chemical Society Reviews,2013,42(3):1287-1311.

[6] Arlett J L,Myers E B,Roukes M L. Comparative Advantages of Mechanical Biosensors[J]. Nature Nanotechnology,2011,6(4):203-215.

[7] 陈雁云,薛长国,黄渊,等. 微悬臂梁传感器对中药成分的非标记检测[J]. 实验力学,2010(5):529-535.

[8] 俞锋,李昕欣,于海涛. 平面内谐振式微悬臂梁生化传感器的设计与制造[J]. 传感技术学报,2012,25(7):869-875.

[9] 刘志伟,童朝阳,穆唏惠,等. 压阻式微悬臂梁传感器检测生化毒剂的响应动力学研究[J]. 传感技术学报,2015,28(9):1297-1302.

[10] Wang Z,Zhao Y. Self-Instability and Bending Behaviors of Nano Plates[J]. Acta Mechanica Solida Sinica,2009,22(6):630-643.

[11] Wang G F,Feng X Q. Effects of Surface Elasticity and Residual Surface Tension on the Natural Frequency of Microbeams[J]. Applied Physics Letters,2007,90(23):231904.

[12] Wang Y,Weissmüller J,Duan H L. Mechanics of Corrugated Surfaces[J]. Journal of the Mechanics and Physics of Solids,2010,58(10):1552-1566.

[13] Zhang N H,Shan J Y. An Energy Model for Nanomechanical Deflection of Cantilever-DNA Chip[J]. Journal of the Mechanics and Physics of Solids,2008,56(6):2328-2337.

[14] Zhang N H,Meng W L,Tan Z Q. A Multi-Scale Model for the Analysis of the Inhomogeneity of Elastic Properties of DNA Biofilm on Microcantilevers[J]. Biomaterials,2013,34(7):1833-1842.

[15] Tan Z Q,Zhang N H,Meng W L,et al. Mechanism for Invalid Detection of Microcantilever-DNA Biosensors due to Environmental Changes[J]. Journal of Physics D:Applied Physics,2016,49(22):225402.

[16] Zhang N H,Wu J Z,Meng W L,et al. Effect of Surface Charge State on the Surface Stress of a Microcantilever[J]. Nanotechnology,2016,27(14):144001.

[17] Ece M C,Aydogdu M,Taskin V. Vibration of a Variable Cross-Section Beam[J]. Mechanics Research Communications,2007,34(1):78-84.

[18] Chen G Y,Thundat T,Wachter E A,et al. Adsorption-Induced Surface Stress and Its Effects on Resonance Frequency of Microcantilevers[J]. Journal of Applied Physics,1995,77(8):3618-3622.

[19] Spletzer M,Raman A,Wu A Q,et al. Ultrasensitive Mass Sensing Using Mode Localization in Coupled Microcantilevers[J]. Applied Physics Letters,2006,88(25):254102.

[20] Morshed S,Prorok B C. Tailoring Beam Mechanics Towards Enhancing Detection of Hazardous Biological Species[J]. Experimental Mechanics,2007,47(3):405-415.

[21] 王大甲,胡放荣,姚军,等. 基于微悬臂梁的化学传感器的灵敏度研究[J]. 传感技术学报,2008,21(8):1333-1336.

[22] Cho H,Jeong B,Yu M F,et al. Nonlinear Hardening and Softening Resonances in Micromechanical Cantilever-Nanotube Systems Originated from Nanoscale Geometric Nonlinearities[J]. International Journal of Solids and Structures,2012,49(15):2059-2065.

[23] Cleveland J P,Manne S,Bocek D,et al. A Nondestructive Method for Determining the Spring Constant of Cantilevers for Scanning Force Microscopy[J]. Review of Scientific Instruments,1993,64(2):403-405.

[24] Sader J E,Chon J W M,Mulvaney P. Calibration of Rectangular Atomic Force Microscope Cantilevers[J]. Review of Scientific Instruments,1999,70(10):3967-3969.

[25] Green C P,Lioe H,Cleveland J P,et al. Normal and Torsional Spring Constants of Atomic Force Microscope Cantilevers[J]. Review of Scientific Instruments,2004,75(6):1988-1996.

[26] Sader J E,Larson I,Mulvaney P,et al. Method for the Calibration of Atomic Force Microscope Cantilevers[J]. Review of Scientific Instruments,1995,66(7):3789-3798.

[27] Sader J E,Sanelli J A,Adamson B D,et al. Spring Constant Calibration of Atomic Force Microscope Cantilevers of Arbitrary Shape[J]. Review of Scientific Instruments,2012,83(10):103705.

[28] Neumeister J M,Ducker W A. Lateral,Normal,and Longitudinal Spring Constants of Atomic Force Microscopy Cantilevers[J]. Review of Scientific Instruments,1994,65(8):2527-2531.

[29] Melcher J,Hu S,Raman A. Equivalent Point-Mass Models of Continuous Atomic Force Microscope Probes[J]. Applied Physics Letters,2007,91(5):053101.

[30] 刘延柱,陈文良,陈立群. 振动力学[M]. 北京:高等教育出版社,1998.

陈金龙(1990-)男,在读硕士研究生,研究方向为生物芯片系统纳米力学,导师为张能辉教授;

吴君正(1992-)男,在读博士研究生,研究方向为生物芯片系统纳米力学,导师为张能辉教授;

张能辉(1970-)男,通讯作者,教授,博士,博士生导师,中国微米纳米技术学会理事,研究方向为生物芯片系统纳米力学和粘弹性结构的非线性振动,nhzhang@shu.edu.cn。

EquivalentStiffnessandNaturalFrequencyofaVariableCross-SectionMicrocantileverSensorwithaHole*

CHENJinlong1,WUJunzheng1,ZHANGNenghui1,2*

(1.Shanghai Key Laboratory of Mechanics in Energy Engineering,Shanghai Institute of Applied Mathematics and Mechanics,Shanghai University,Shanghai 200072,China;2.Department of Mechanics,College of Sciences,Shanghai University,Shanghai 200444,China)

This paper focuses on the equivalent normal stiffness of a new-type variable cross-section microcantilever biosensor with a hole and its effect on the natural frequency. First,considering the bending-torsion coupling effect induced by the cavity structure in the longitudinal cross-section of the micro-beam,the cantilever deflection subjected to a concentrated load at the free-end is obtained by the quadratic integral method. Based on the Hooke’s law of elastic material,an analytic model is established for the equivalent normal stiffness of the micro-beam. Thereafter,the natural frequency of the micro-beam is obtained by the Rayleigh’s method. Finally,the analytical model is verified by comparing with the relevant experimental results and finite element results. The study show that the analytical model has a good accuracy for predicting and calibrating the stiffness,as well as the frequency of the variable cross-section micro-beam with a hole,and the equivalent stiffness and the natural frequency are negatively correlated with the span-to-width ratio,whereas,positively correlated with the inner-to-outer-width ratio. The relevant conclusions can provide a theoretical basis and reference for the design of new-type micro-/nano-mechanical sensors with variable cross-sections.

microcantilever sensors;variable cross-section;equivalent stiffness;natural frequency;analytical method

项目来源:上海市浦江人才计划项目(15PJD016);国家自然科学基金项目(11272193)

2017-03-09修改日期:2017-05-22

TP212.3;O39

:A

:1004-1699(2017)09-1324-06

10.3969/j.issn.1004-1699.2017.09.004