基于鲁棒主成分分析的智能电网虚假数据注入攻击

田继伟，王布宏，尚福特

(空军工程大学 信息与导航学院，西安 710077) (*通信作者电子邮箱tianjiwei2016@163.com)

基于鲁棒主成分分析的智能电网虚假数据注入攻击

田继伟*，王布宏，尚福特

(空军工程大学 信息与导航学院，西安 710077) (*通信作者电子邮箱tianjiwei2016@163.com)

基于主成分分析(PCA)的盲攻击策略仅对具有高斯噪声的测量数据有效，在存在异常值的情况下，上述攻击策略将被传统的坏数据检测模块检测。针对异常值存在的问题，提出一种基于鲁棒主成分分析(RPCA)的盲攻击策略。首先，攻击者收集含有异常值的测量数据；然后，通过基于交替方向法(ADM)的稀疏优化技术从含有异常值的测量数据中分离出异常值和真实的测量数据；其次，对真实测量数据进行PCA，得到系统的相关信息；最后，利用获得的系统信息构造攻击向量，并根据得到的攻击向量注入虚假数据。该攻击策略在IEEE 14-bus系统上进行了测试，实验结果表明，在异常值存在的情况下，传统的基于PCA的攻击方法将被坏数据检测模块检测，而所提方法基于鲁棒PCA的攻击策略能够躲避坏数据检测模块的检测。该策略使得在异常值存在的情况下虚假数据注入攻击(FDIA)仍然能够成功实施。

虚假数据注入攻击；鲁棒主成分分析；交替方向法；坏数据检测；状态估计

0 引言

电力系统是国家最关键的基础设施之一，其安全稳定运行对社会稳定和国民经济快速健康发展起关键作用。随着各种信息通信技术在电力系统的广泛应用，智能电网得到了迅速发展，电力系统的效率和可靠性得到了显著提升，但与此同时，电力系统遭受网络攻击的可能性也显著增加[1-2]。最近的研究表明，智能电网面临着各种各样的网络攻击的威胁[3]，如拒绝服务攻击、数据窃听、虚假数据注入攻击(False Data Injection Attack, FDIA)[4]等。

2009年，文献[4]首次提出了虚假数据注入攻击(FDIA)的概念。该种攻击利用了状态估计中不良数据检测模块的漏洞，攻击者通过向量测数据中注入虚假的数据，可以达到改变状态变量、控制系统的运行状态以及获取经济利益等目的[5]。虚假数据注入攻击关联性高，隐蔽性强，对电力系统危害极大，甚至能引发大停电事故，因此，虚假数据注入攻击一经提出便引起了学术界的广泛重视，研究者开始从各个角度展开研究。目前，关于如何构建虚假注入数据的研究可以分为两类：1)攻击者掌握了电网的拓扑信息和各种电气参数[4,6]；2)攻击者事先并不知晓电网的拓扑信息和各种电气参数，仅仅依靠观测的量测信息构建攻击向量[7-8]。第一类攻击得到了广泛深入的研究，文献[4]和[6]对攻击者在完全掌握电力系统信息的条件下如何构造攻击向量进行了研究；文献[9]提出了一种改进的虚假数据注入攻击，该种攻击可以在得知部分电力系统信息的条件下成功进行。然而，上述攻击向量的构造均依赖于电网的拓扑信息和各种电气参数，这些信息通常都会进行严格的管理，攻击者很难掌握，因此该类攻击的实际可行性大大受限。2015年，文献[7]和[8]对第二类攻击进行了研究，该类攻击使用子空间变换法(如主成分分析(Principal Component Analysis, PCA)构造攻击向量，其虚假数据的构造仅仅依赖于观测的量测信息矩阵，相对于第一类攻击，该类攻击现实可行性更高，其对电力系统的威胁也更大。

本文首先对状态估计和坏数据检测进行了简单的介绍，然后对文献[8]中基于主成分分析的虚假数据注入攻击进行分析，当测量信息中含有异常值(由于传感器的错误连接、偏移、设备故障、通信系统受到干扰等原因)时，该类攻击会被坏数据检测模块成功检测。最后，本文基于交替方向法(Alternating Direction Method, ADM)[10]，提出基于鲁棒主成分分析(Robust Principal Component Analysis， RPCA)的虚假数据注入攻击策略，即使在含有异常值的情况下，仍然可以躲避检测成功实施攻击。为了证明该攻击的有效性，在IEEE 14-bus系统上进行了仿真实验，并与其他攻击方法进行了对比分析。

1 状态估计和坏数据检测

1.1 状态估计

电力系统状态估计是能量管理系统(Energy Management System， EMS)和广域监测系统(Wide Area Measurement System， WAMS)执行最优潮流计算、负荷预测和暂态稳定分析等相关分析控制功能的基础，主要作用包括提高量测数据的精度、推算出准确的电力系统的各种电气参数和提高数据采集与监视控制系统(Supervisory Control And Data Acquisition, SCADA)的可靠性等[11]。在具有N条母线的电力系统中，状态变量一般取为母线的复电压，包括电压的幅值和相角，除去参考节点，一共有2N-1个状态变量，统一表示为x=[x1,x2,…,xn]T，n=2N-1。量测值一般为母线的注入有功和无功功率、支路有功和无功功率或母线电压幅值，假如有m个量测值，并且m>n，量测值可统一表示为z=[z1,z2,…,zm]T，则状态变量和量测值的关系可以表示为：

z=h(x)+e;e≈N(0,Σe)

(1)

一个正常稳定运行的电力系统，其母线的电压在额定电压附近，且支路两端的相角差很小，而且对于超高压电力网，支路的电阻比电抗小得多，因此，假设所有母线的电压的幅值相等且均为1，忽略线路的电阻，则测量值中不存在无功功率，状态变量只有电压相角。此时，状态变量和量测值之间满足线性关系，得到式(2)所示的直流潮流方程:

z=Hx+e

(2)

其中：z为量测值，H为测量雅可比矩阵，x为待估计的状态量，e为测量误差。电力系统状态估计问题以冗余的测量值为基础(rank(H)=n)，可以通过加权最小二乘法(Weighted Least-Squares, WLS)来获得状态变量的估计值：

(3)

1.2 坏数据检测

由于状态估计以冗余的测量值为基础，其中的测量值可能含有坏数据或者恶意数据，这就需要检测坏数据并加以剔除，以确保状态估计结果的可靠性。为消除不良数据对状态估计的影响，以残差方程为基础的不良数据检测方法得到了广泛应用。残差的表达式为:

(4)

检测坏数据的判据是：‖r‖<τ，τ为判断的阈值。如果‖r‖<τ成立，认为没有坏数据；否则就要剔除相应的坏数据并重新进行状态估计，直到通过坏数据检测为止[12]。

虚假数据注入攻击FDIA就是利用了该检测方法的缺陷，若用a=[a1,a2,…,am]T表示攻击者在量测值中注入的虚假数据向量，则实际的测量数据为zbad=z+a，此时估计的状态变量为xbad=x+c，c=[c1,c2,…,cn]T表示由于虚假数据的注入在状态变量中引入的误差向量。此时残差表达式为：

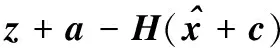
(5)

显然，当a=Hc时，有式(6)成立：

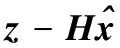
(6)

此时，采用基于残差的不良数据检测方法无法发现测量数据中的虚假数据，攻击者可以将量测值和状态变量修改为任意值，危害到电力系统的安全稳定运行。

2 基于主成分分析的虚假数据注入攻击

基于主成分分析的虚假数据注入攻击属于盲虚假数据注入攻击，该类攻击向量的构造仅仅依赖于测量信息矩阵，是一种数据驱动的方法。由于短时间内，电力系统的负荷变化很小，而且系统的拓扑短期内也会保持不变，这使得通过测量信息的相关性来估计系统的相关信息成为可能[7-8,13]。

用z1,z2,…,zK表示在K个采样时刻分别观察到的测量向量，由式(2)得：

zi=Hxi+ei;i=1,2,…,K

(7)

这里假设噪声向量e1,e2,…,eK独立同分布，状态变量x1,x2,…,xK独立同分布，其协方差矩阵为正定矩阵Σx，且噪声和状态变量是不相关的，则测量信息矩阵z=[z1,z2,…,zK]，其协方差[7]为：

Σz=E[(z1-E[z1])(z1-E[z1])T]=HΣxHT+σ2I

(8)

如果矩阵的列空间(column space)表示为C(·),则C(HΣxHT)等价于C(H)。其中，HΣxHT秩为n，由n个最大的奇异值可对应求得列空间C(HΣxHT)的基，因此，可以通过奇异值分解的方法求得列空间Σz的基，由于C(HΣxHT)等价于C(H)，这同时也是C(H)的基。求得C(H)的基之后，便可以利用它进行攻击向量的构造。文献[7]和文献[8]分别通过奇异值分解和主成分分析的方式进行了攻击向量的构造。下面，对文献[8]采用的主成分分析方法进行简单介绍。

考虑测量信息矩阵ZK×m，行表示某一时刻的观测，列表示某一测量单元。随后，用主成分分析法对矩阵ZK×m进行处理。主成分分析是一种统计方法，通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。经过主成分分析处理后，可以得到主成分x和变换矩阵PT[8]。其相互关系为：

PTZ=x

(9)

此时，测量信息矩阵Z可以近似表示为:

(10)

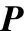
apca=Hpcac

(11)

c是任意的非零列向量[8]，则篡改后的测量信息为zpca=z+apca。

在测量信息矩阵中，由于设备故障、通信链路故障等原因，常常存在一些异常值。由于传统主成分分析鲁棒性较差，故存在异常值的情况下，上述攻击方法很难躲避坏数据检测模块的检测，因此，有必要对上述攻击方法进行改进，使得异常值存在时，仍然能够实施攻击而不被系统所发现。

3 基于RPCA的虚假数据注入攻击

在测量信息仅仅含有高斯噪声的情况下，基于主成分分析的攻击方法是有效的，但在存在异常值的情况下，上述攻击方法很容易被坏数据检测模块检测。其本质原因在于存在异常值的情况下，传统主成分分析方法鲁棒性较差[14]。即使存在较少的异常值，上述攻击策略也可能无法实施。然而，如果使用鲁棒主成分分析(RPCA)，攻击者仍然可以在存在异常值的情况下成功实施攻击行为。

含异常值的矩阵可以表示为：

Z=A+E

(12)

其中：A是原始的低秩矩阵，E是代表异常值的稀疏矩阵，Z表示攻击者真实观测到的含有异常值的测量矩阵。攻击者首先需要在测量矩阵Z中对A和E进行分离，以便恢复出低秩矩阵A。这可以看成一个典型的低秩矩阵恢复问题。

从数学上来讲，将一个矩阵Z分解为一个低秩矩阵A和一个稀疏矩阵E的问题可以由下述优化问题来描述：

s.t.Z=A+E

(13)

然而，由于目标函数中rank(A)和‖E‖0都是非线性非凸的组合优化函数，对上述问题的求解是十分困难的[15]。

借鉴压缩感知和矩阵秩最小化方面的研究成果，人们转而求解下述凸优化问题：

s.t.Z=A+E

(14)

在该凸优化问题中，‖·‖*和‖·‖1分别表示矩阵的核范数和l1范数，λ是值大于0的加权参数。本文使用交替方向法(ADM)[10]对该问题进行求解。

首先构造增广拉格朗日函数：

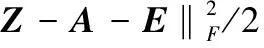
(15)

(16)

(17)

(18)

最后更新参数μ：

(19)

其中：ρ>1为常数，ε<0为比较小的正数。按照上述步骤交替迭代矩阵A和E，直到满足终止条件为止。

通过低秩矩阵恢复得到A之后，便可通过矩阵A进行攻击向量的构建。整个流程如图1所示。

图1 基于RPCA的攻击流程

4 仿真分析

仿真实验分为3部分：首先，基于主成分分析的方法设计攻击向量，进行虚假数据注入攻击，并与掌握系统信息下的虚假数据注入攻击进行比较；其次，通过实验验证在异常值存在的情况下，基于主成分分析的攻击策略因很容易被检测出来而无法实施；最后，基于交替方向法(ADM)，使用鲁棒主成分分析的方法设计攻击向量，进行虚假数据注入攻击，此时即使在含有异常值的情况下，仍然可以躲避检测成功实施攻击。

图2 IEEE 14-bus系统

4.1 基于主成分分析的虚假数据注入攻击(无异常值)

当系统正常运行(无攻击)时，状态估计能够较好地估计系统的状态变量，测量值和测量估计值基本保持一致，如图3(a)和3(c)所示，此时残差为3.13，低于阈值。

如果攻击者在掌握系统信息的情况下实施虚假数据注入攻击，则系统的状态变量估计值和真实值有较大改变，但测量值和测量估计值基本保持一致，如图3(b)和3(d)，此时残差保持不变，这意味着攻击者能够在残差保持不变的情况下改变状态估计的结果以达到其攻击目的。

图3 无攻击和得知系统信息下的FDIA

但如果攻击者在不掌握系统信息的情况下随意注入攻击向量，则很容易被检测到，如图4(a)和4(c)所示，此时测量值和测量估计值有较大偏差，残差为5.35E+6,远远超过阈值。在事先不掌握系统信息的条件下，如果攻击者使用基于主成分分析的攻击策略(不含异常值)，仍然可以成功实施攻击，如图4(b)和4(d)所示，此时状态变量估计值得到了篡改，但是测量值和测量估计值仍然保持着较好的一致性，残差为15.5，低于阈值。这里攻击者观测了100个时刻的测量信息。

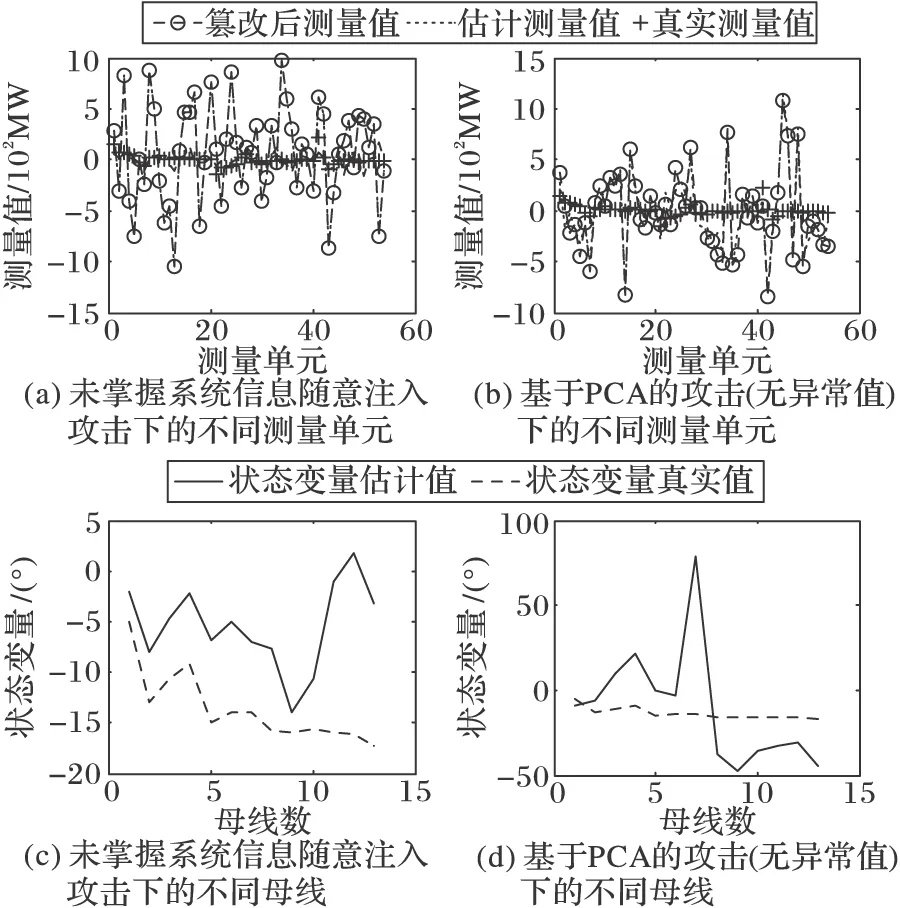
图4 随意的FDIA和基于PCA的FDIA(无异常值)

4.2 基于主成分分析的虚假数据注入攻击(有异常值)

在存在异常值的情况下(这里将异常值设为比正常值大很多的数据，异常值出现的概率设为1%)，基于主成分分析的攻击策略很容易被发现。如图5(a)和5(c)所示，此时虽然仿真结果中状态变量估计值和真实值有较大变化，但是测量值和测量估计值并不重合，反而差异很大，残差为2.5E+5,远远超过阈值，这意味着该攻击将被坏数据检测模块成功检测而无法实现攻击目的。造成此结果的原因是由于在存在异常值时，传统的主成分分析法缺乏鲁棒性，也就是说在存在异常值时传统主成分分析法得到的矩阵Hpca(图6,见式(11))并不能较为准确地反映测量信息矩阵的真实关联关系。

图5 基于PCA和基于RPCA的FDIA(有异常值)

图6 PCA得到的矩阵Hpca

4.3 基于鲁棒主成分分析的虚假数据注入攻击(有异常值)

在存在异常值的情况下，如果使用基于鲁棒主成分分析的攻击策略，则可以避免被发现从而成功实施攻击。

基于鲁棒主成分分析的攻击策略，在进行传统的主成分分析之前，将首先对含有异常值的观测信息矩阵Z(图7)进行低秩恢复，以得到稀疏矩阵E(图8)和低秩矩阵A(图9)。然后再对低秩矩阵A进行主成分分析，以便进行后续的攻击向量的构造。经过低秩矩阵恢复的过程，将使得该种攻击策略在异常值存在的情况下鲁棒性大大增加。

如图5(b)和5(d)所示，虽然存在异常值，基于鲁棒主成分分析的攻击策略仍然能够在改变状态变量估计值的情况下保持测量值和测量估计值的一致性，此时残差为13.38，低于阈值，这意味着该种攻击策略在异常值存在的情况下仍然可以躲避检测达到其攻击目的。

图7 攻击者观测到的测量矩阵Z(含异常值)

图8 测量矩阵Z中恢复出来的稀疏矩阵E

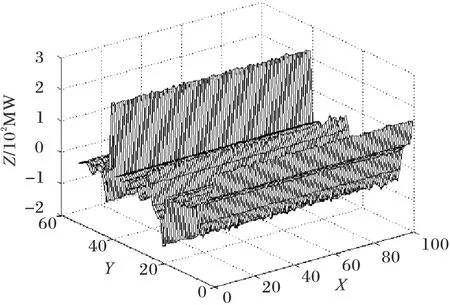
图9 测量矩阵Z中恢复出来的低秩矩阵A

图10是该种攻击策略下得到的矩阵Hrpca(这里记为Hrpca，见式(11))。

图10 鲁棒主成分分析得到的矩阵Hrpca

对比图6和图10，发现两种策略下得到的矩阵有较大差异，由于图10是异常值剔除后得到的矩阵，故能较为准确地反映测量信息矩阵的真实关联关系，这也是该种攻击策略在异常值存在的情况下能够成功实施的原因。

5 结语

传统的虚假数据注入攻击需要攻击者掌握电力系统拓扑和电气参数等信息。本文对不需要上述信息的基于主成分分析的盲攻击策略进行了研究，发现当测量信息中存在异常值时，基于主成分分析的攻击策略很容易被发现而无法成功实施，因此，本文基于交替方向法，提出了基于鲁棒主成分分析的攻击策略，即使存在异常值，该策略仍然可以成功实施。下一步，将对如何检测和预防此类攻击进行研究。

References)

[1] 汤奕,王琦,倪明,等.电力信息物理融合系统中的网络攻击分析[J].电力系统自动化,2016,40(6):148-151.(TANG Y, WANG Q, NI M, et al. Analysis of cyber attacks in cyber physical power system [J]. Automation of Electric Power Systems, 2016, 40(6): 148-151.)

[2] 倪明,颜诘,柏瑞,等.电力系统防恶意信息攻击的思考[J].电力系统自动化,2016,40(5):148-151.(NI M, YAN J, BO R, et al. Power system cyber attack and its defense [J]. Automation of Electric Power Systems, 2016, 40(5): 148-151.)

[3] 刘念，余星火，张建华.网络协同攻击：乌克兰停电事件的推演与启示[J].电力系统自动化，2016,40(6)：144-147.(LIU N, YU X H, ZHANG J H. Coordinated cyber-attack: inference and thinking of incident on Ukrainian power grid [J]. Automation of Electric Power Systems, 2016, 40(6): 144-147.)

[4] LIU Y, NING P, REITER M K. False data injection attacks against state estimation in electric power grids [C]// Proceedings of the 16th ACM Conference on Computer and Communications Security. New York: ACM, 2011: 21-32.

[5] 王先培,田猛,董政呈,等.输电网虚假数据攻击研究综述[J].电网技术,2016,40(11):3406-3414.(WANG X P, TIAN M, DONG Z C, et al. Survey of false data injection attacks in power transmission systems [J]. Power System Technology, 2016, 40(11): 3406-3414.)

[6] XIE L, MO Y L, SINOPOLI B. False data injection attacks in electricity markets [C]// SmartGridComm2010: Proceedings of the 2010 IEEE International Conference on Smart Grid Communications. Piscataway, NJ: IEEE, 2010: 226-231.

[7] KIM J, TONG L, THOMAS R. Subspace methods for data attack on state estimation: a data driven approach [J]. IEEE Transactions on Signal Processing, 2015, 63(5): 1102-1114.

[8] YU Z H, CHIN W L. Blind false data injection attack using PCA approximation method in smart grid [J]. IEEE Transactions on Smart Grid, 2015, 6(3): 1219-1226.

[9] RAHMAN M, MOHSENIAN-RAD H. False data injection attacks with incomplete information against smart power grids [C]// GLOBECOM 2012: Proceedings of the 2012 IEEE Global Communications Conference. Piscataway, NJ: IEEE, 2012: 3153-3158.

[10] YUAN X M, YANG J F. Sparse and low-rank matrix decomposition via alternating direction methods [J]. Pacific Journal of Optimization, 2009, 9(1): 1-11.

[11] 赵俊华,梁高琪,文福拴,等.乌克兰事件的启示:防范针对电网的虚假数据注入攻击[J].电力系统自动化,2016,40(7):149-151.(ZHAO J H, LIANG G Q, WEN F S, et al. Lessons learnt from the Ukrainian blackout: protecting power grids against false data injection attacks [J]. Automation of Electric Power Systems, 2016, 40(7): 149-151.)[12] 朱杰,张葛祥,王涛,等.电力系统状态估计欺诈性数据攻击及防御综述[J].电网技术,2016,40(8):2406-2415.(ZHU J, ZHANG G X, WANG T, et al. Overview of fraudulent data attack on power system state estimation and defense mechanism [J]. Power System Technology, 2016, 40(8): 2406-2415.)

[13] ESMALIFALAK M, NGUYEN H, ZHENG R, et al. Stealth false data injection using independent component analysis in smart grid [C]// SmartGridComm 2011: Proceedings of the 2011 International Conference on Smart Grid Communications. Piscataway, NJ: IEEE, 2011: 244-248.

[14] CANDES E J, LI X, MA Y, et al. Robust principal component analysis? [J]. Journal of the ACM, 2009, 58(3): Article No. 11.

[15] 彭义刚,索津莉,戴琼海,等.从压缩传感到低秩矩阵恢复:理论与应用[J].自动化学报,2013,39(7):981-994.(PENG Y G, SUO J L, DAI Q H, et al. From compressed sensing to low-rank matrix recovery: theory and applications [J]. Acta Automatica Sinica, 2013, 39(7): 981-994.)

[16] ZIMMERMAN R D, MURILLO-SNCHEZ C E, THOMAS R J. MATPOWER: steady-state operations, planning, and analysis tools for power systems research and education [J]. IEEE Transactions on Power Systems, 2011, 26(1): 12-19.

[17] University of Washington. Power systems test case archive [EB/OL]. [2016- 12- 20]. http://www.ee.washington.edu/research/pstca/.

This work is partially supported by the National Natural Science Foundation of China (61272486), the Open Research Fund Program of State Key Laboratory of Information Security (2014- 02).

TIANJiwei, born in 1993, M. S. candidate. His research interests include network security, smart grid security.

WANGBuhong, born in 1975, Ph. D., professor. His research interests include signal processing, information security, smart grid security.

SHANGFute, born in 1992, Ph. D. candidate. His research interest include information security, smart grid security.

Falsedatainjectionattacksbasedonrobustprincipalcomponentanalysisinsmartgrid

TIAN Jiwei*, WANG Buhong, SHANG Fute

(CollegeofInformationandNavigation,AirForceEngineeringUniversity,Xi’anShaanxi710077,China)

The blind attack strategy based on Principal Component Analysis (PCA) is only effective for the measurement data with Gaussian noise. In the presence of outliers, the attack strategy will be detected by the traditional bad data detection module. Aiming at the problem of outliers, a blind attack strategy based on Robust PCA (RPCA) was proposed. Firstly, the attacker collected the measurement data with outliers. Then, the outliers and the real measurement data were separated from the measurement data containing outliers by the sparse optimization technique based on the Alternating Direction Method (ADM). Secondly, the PCA technique was carried out on the real measurement data, and the relevant information of the system was obtained. Finally, the acquired system information was used to construct the attack vector, and the false data was injected according to the attack vector. The experimental results show that the traditional attack method based on PCA will be detected by the bad data detection module in the presence of outliers, and the proposed method based on robust PCA can avoid the detection of bad data detection module. This strategy makes it possible to successfully implement False Data Injection Attack (FDIA) in the presence of outliers.

False Data Injection Attack (FDIA); Robust Principal Component Analysis (RPCA); Alternating Direction Method (ADM); bad data detection; state estimation

TM72; TP309.2

:A

2017- 02- 04;

:2017- 03- 09。

国家自然科学基金资助项目(61272486)；信息安全国家重点实验室开放课题基金资助项目(2014- 02)。

田继伟(1993—)，男，河南驻马店人，硕士研究生，主要研究方向：网络安全、智能电网安全； 王布宏(1975—)，男，山西太原人，教授，博士生导师，博士，主要研究方向：信号处理、信息安全、智能电网安全； 尚福特(1992—)，男，山东泰安人，博士研究生，主要研究方向：信息安全、智能电网安全。

1001- 9081(2017)07- 1943- 05

10.11772/j.issn.1001- 9081.2017.07.1943