水平气流中微波折射率结构常数建模

仓蕾,赵恒凯,郑国莘

(1.上海大学通信与信息工程学院,上海200444; 2.上海大学特种光纤与光接入网省部共建重点实验室,上海200072)

水平气流中微波折射率结构常数建模

仓蕾1,2,赵恒凯1,2,郑国莘1,2

(1.上海大学通信与信息工程学院,上海200444; 2.上海大学特种光纤与光接入网省部共建重点实验室,上海200072)

电磁波在大气中传输时会受到大气湍流的影响,湍流的强弱可以用折射率结构常数C2n来表示.在2.4 GHz的微波环境下,重点研究了微波段空气中水汽压对大气折射率结构常数的影响.温湿度结构常数的计算选择湍流动能(turbu lence kinetic energy,TKE)闭合方案,由耗散率方法求得,修正了干燥空气的归一化公式,在水平气流环境中构建了微波折射率结构常数的模型.结合隧道环境中实测的气象参数,采用该模型分析实验时的微波折射率结构常数,得到在2.4 GHz的微波环境下,湿度对折射率结构常数的贡献大于温度.

折射率结构常数;微波;水平气流;水汽压

人类活动和太阳辐射等因素所产生的大气微小随机变化形成了大气湍流运动.这些变化的累积效应会导致大气折射率在时间和空间上产生随机起伏,由此引起波束漂移、闪烁、波束扩展等一系列大气湍流效应.闪烁是由振幅的随机起伏引起的,它会降低信噪比,影响通信质量.折射率结构常数可以导出电磁波传播的闪烁指数和相位起伏,所以对其进行研究可以为提高通信质量提供一定的理论支持[1].雷诺是最早对湍流进行研究的,他通过圆管试验证明了湍流运动可以用一个无量纲的雷诺数来表述[2].Tatarskii采用Rytov近似法并引入现代湍流统计理论,通过常规气象参数计算光波段的折射率结构常数,获得了相当的成功.Thiermann等[3]通过海上实验发现相似性函数的经验公式符合-2/3次幂,由此得到海气界面上的折射率结构常数模型.基于此,Hutt[4]推出了近地面的折射率结构常数模型.ITU-R[5]通过实验发现,折射率结构常数与局部大气条件和离开地面的高度有关,并提出了折射率结构常数的一般表达式.Cheinet等[6]通过波传输理论研究了闪烁率和传输距离的关系,发现折射率结构常数随高度的降低而减小.Maronga等[7]采用小波分析理论和局部耗散率的方法,使用大涡模拟估算了温湿度结构常数的值,结果和大孔径闪烁仪的观测值完全一致.由于对光波在垂直方向上的折射率结构常数研究已经比较深入,本工作应用相似性原理在水平气流环境下的水平方向上建立模型,以期为后续的研究提供理论参考.

1 微波的折射率结构常数

1.1 折射率结构常数的估算

在自由大气中,折射率的变化是由大气中环境(主要指大气中温度、湿度、压强等)的变化引起的,即

式中,n为空气中的折射率,T,Q和P分别表示温度、湿度和大气压.

根据统计平均的理论,湍流的物理量可以分解为平均值和脉动值.将式(1)进行泰勒多项式展开,并且只保留第一阶,可以得到

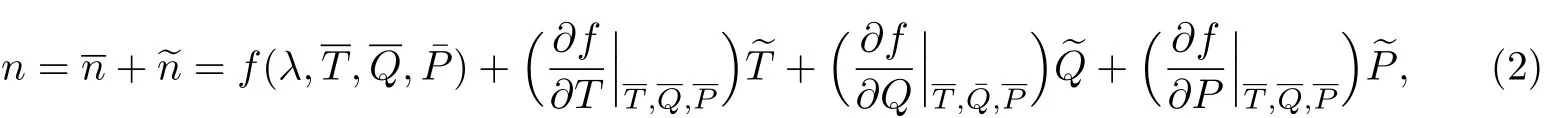
将脉动项提取出来,并且忽略大气压脉动的微小影响[8],式(2)可以简单地写为

式中,

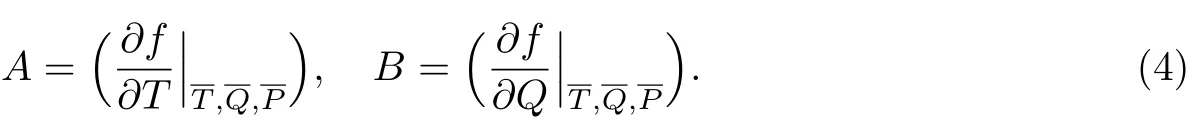
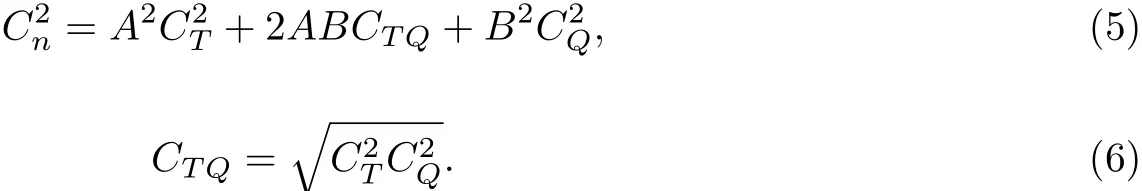
1.2 微波环境下气象参数的选取

在光波段和微波段,折射率结构常数有着很大的不同,主要是因为水蒸气对于光的色散作用而使其受到湿度的影响.在光波段,湿度对折射率结构常数的影响可以忽略;而在微波段,湿度对大气折射率的起伏有着重要的作用,甚至在湿度较大的地区成为影响折射率结构常数的主要因素.本工作在求解折射率时把全部空气分成三部分来处理,分别是无水蒸气无CO2的空气、CO2、水蒸气.用P表示总大气压,这三部分的分压力分别表示为P1,P2和e[9].室外一般取CO2含量为0.03%,即P2=P-P1-e=P×0.03%.

微波段的干燥空气折射率的归一化表达式可以写为

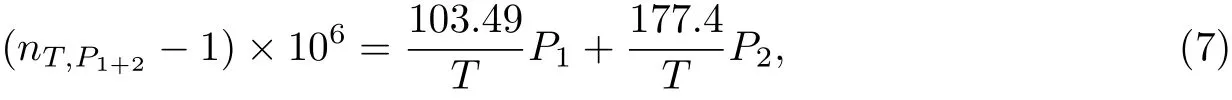
式中,nT,P1+2表示温度为T时干燥空气的折射率.

下面计算空气中的水蒸气对折射率的影响.介电常数与温度和水汽压的关系[10]为

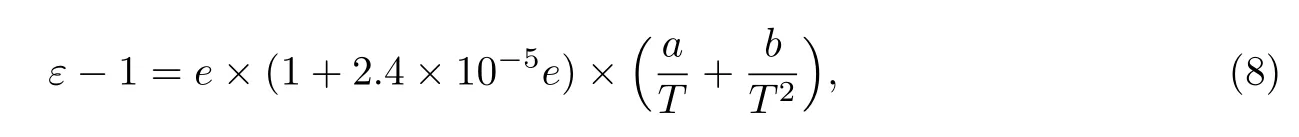
式中,ε为介电常数,系数a表示原子和电子的极化对介电常数的影响,b表示电偶极子对介电常数的影响.在光波段,b=0;在微波段,一般取经验值b=0.991 3[10].

根据Barrell等[11]给出的方法,在频率为2.4 GHz的微波段取温度平均值为10.5◦C、相对湿度平均值为31%,查表得到相应的绝对湿度Q约为2.92×10-3kg/m3,即e=0.382 kPa,得到a=1.721 8×10-4.水汽压引起的折射率可以表示为

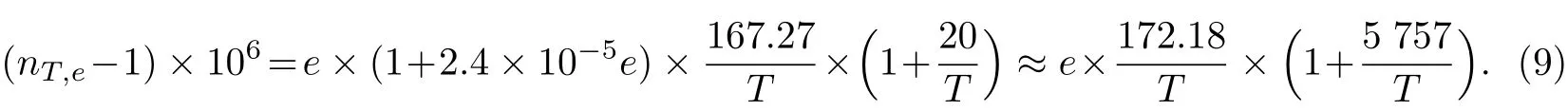
综合式(7)和(9),可以得到微波段折射率的归一化一般公式为

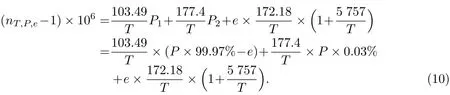
换算为折射率和温湿度压强的关系,并对温湿度求偏导得到

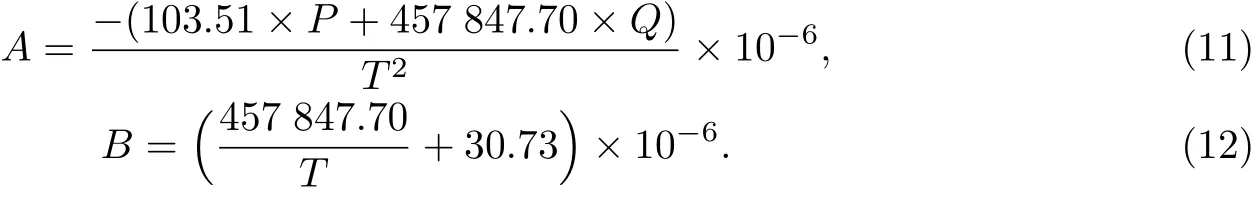
1.3 耗散率方法推导结构常数

式中,S表示标量,可以是温度、湿度或者温湿掺混,Δx表示测量的分辨率,β≈0.4是常数, εTKE和εS分别表示湍流动能和标量方差的耗散率.

在分辨率范围内的εTKE计算方法类似于荷兰大气大涡模拟(Dutch atmospheric largeeddy simulation,DALES)模型[13],εS可以运用等效耗散和平均梯度的关系来计算.二者分别表示为

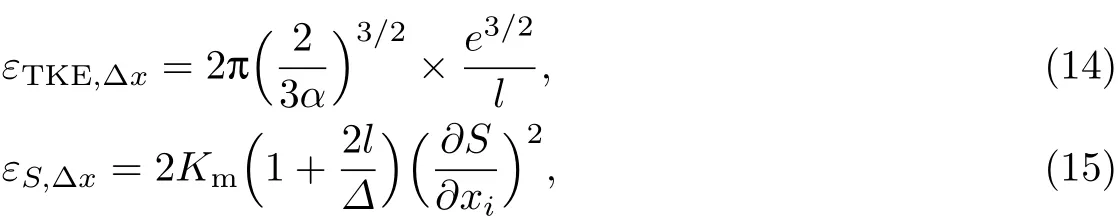
式中,α≈0.52为常数,l为混合长度,e为湍流动能,Km为湍流动能交换系数.在湍流K理论(K theory of turbulence)的闭合方案中,使用频繁的是TKE闭合方案.它源于Kolmogorov的湍流理论,认为Km与湍流动能的平方根成正比,从量纲角度考虑,中间还有个混合长度l,即

式中,c0=0.1为常数,混合长度l依赖于大气的高度和分层情况,在稳定和不稳定的情况下有不同的取值[14].

综上,结构常数可以表示为

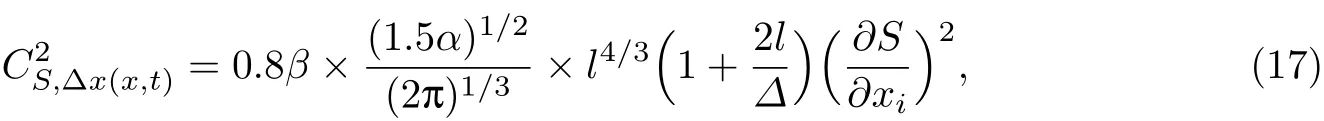
式中,混合长度l取

由于结构常数都是一维方向(顺气流方向)上的参数[15],而目前垂直方向模型都是应用在从地面到数百米高空.在这个场景下,存在的是垂直方向的气流,这些模型也都是建立在假设水平均匀的条件下.两个相似的流动现象都属于同一类物理现象,都应用同一类数学物理方程所描述.因此在水平风的条件下,运用这种原理,可假设在与风向垂直的截面上流场是均匀的.若气流方向是y,则v′θ′即为穿过这个截面沿坐标方向的热通量,热通量对坐标微分引起温度的变化.若不计分子热传导、辐射,则在只考虑热通量沿坐标变化时,通过一阶湍流K理论闭合,水平湍流热通量可以写成所以在水平气流环境下,也是成立的.

1.4 数值分析

由式(5)可知,A和B分别是温度和湿度结构常数的系数,通过比较可以分别看出温度和湿度对折射率结构常数的贡献大小.图1是在频率为2.4 GHz的微波段，不同温度、湿度情况下的结构常数系数曲线.可以看出,无论是温度还是湿度变化,湿度结构常数系数B都明显大于温度结构常数系数A,在数量级上有较大的差异.因此可以得出结论,在频率为2.4 GHz的微波段下,湿度对折射率结构常数的贡献大于温度.

图2是相距10 m的两点之间的温度起伏对微波折射率结构常数C2n的影响.图2(a)假设两点的湿度分别为0.002和0.004 kg/m3,其中一点的温度为10◦C,另一点的温度由横坐标表示.图2(b)假设两点的温度分别为10和15◦C,其中一点的水汽压为1.33 kPa,另一点的水汽压由横坐标表示.绿色实线、红色和蓝色虚线分别表示稳定和非稳定状态下风速为15和20 m/s时的折射率结构常数.

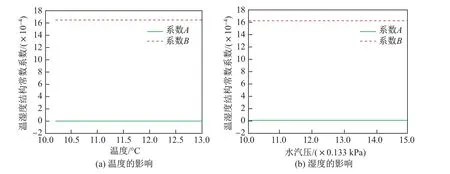
图1 温湿度结构常数系数Fig.1 Coeffi cients of temperature and humidity structure constant

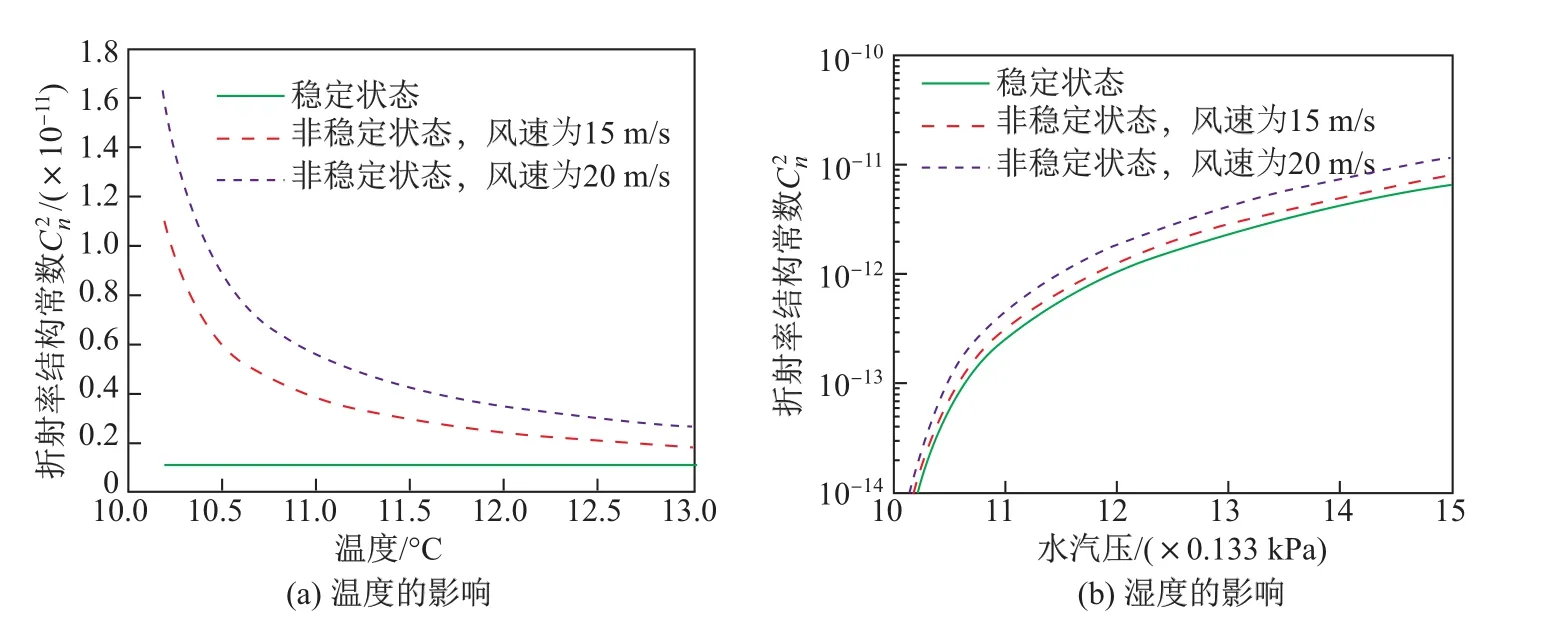
图2 温湿度变化对折射率结构常数的影响Fig.2 In fluences on refractive index structure constant made by temperature and humidity

由图2可以看出,频率为2.4 GHz时的微波折射率结构常数在非稳定大气状态下的值要高于稳定状态,并且随风速的加快而增大.在大气稳定状态下,都是随着空间上温湿度起伏的增大而增大.湿度在大气非稳定状态下也符合这个规律,但温度则呈现相反的趋势.结合图1以及式(17)～(18)可知,这是由于湿度结构常数系数B远大于温度结构常数系数A,从而造成式(5)中第三项远大于前两项,而第三项中湿度结构常数在非稳定状态下是随温度起伏的增大而减小的.

2 实测分析

2014年12月6日,在原上海市闸北区西藏北路隧道进行了实验,得到了10 min的数据.采集仪的温湿度传感器都位于距离地面高度为1m的位置,选取的两个传感器之间的距离为15m,输入参数有温度、相对湿度、风速.计算时,将相对湿度转换为绝对湿度,数据采集频率为2次/s,风向与隧道平行.采集到的温湿度和风速的数据如图3～5所示.

根据式(11)和(12),结合实测数据,得到湿温度结构常数系数的概率密度分布图(见图6).对比图6(a)和(b)可以看出,温湿度结构常数系数A和B在数量级上有很大的差异,系数A主要分布在-2.2×10-9左右,系数B主要分布在-1.646 5×10-3左右.由式(5)可知,系数A和B分别表示温湿度对折射率结构常数的贡献大小.在本实验环境中,湿度在2.4 GHz微波段对微波的折射率结构常数的贡献远远大于温度.

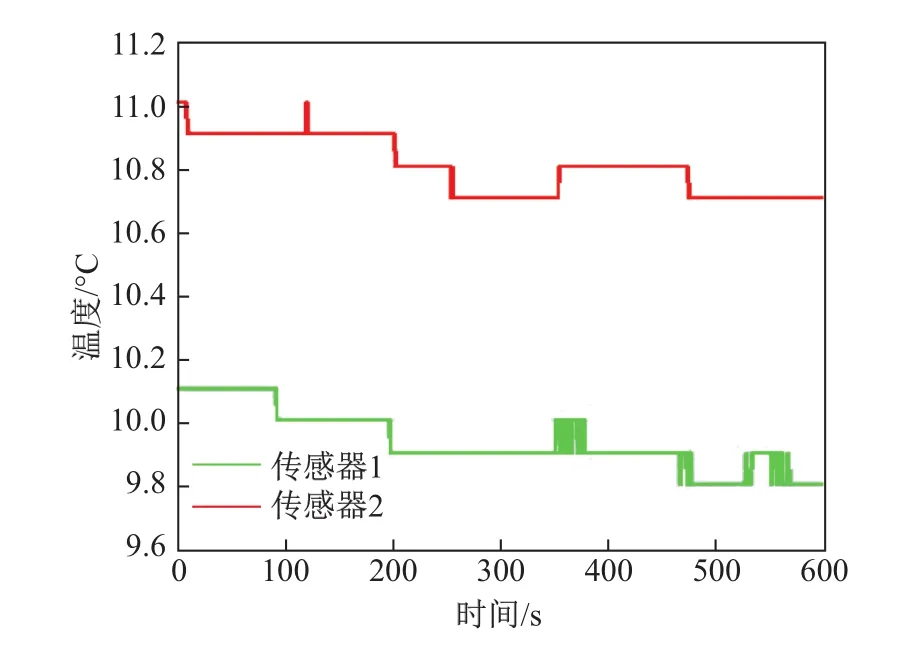
图3 隧道实验温度实测结果F ig.3 Temperature experiment resu lts in the tunnel

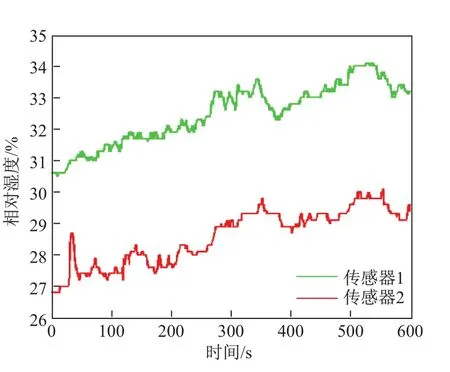
图4 隧道实验湿度实测结果F ig.4 Humidity experiment resu lts in the tunnel

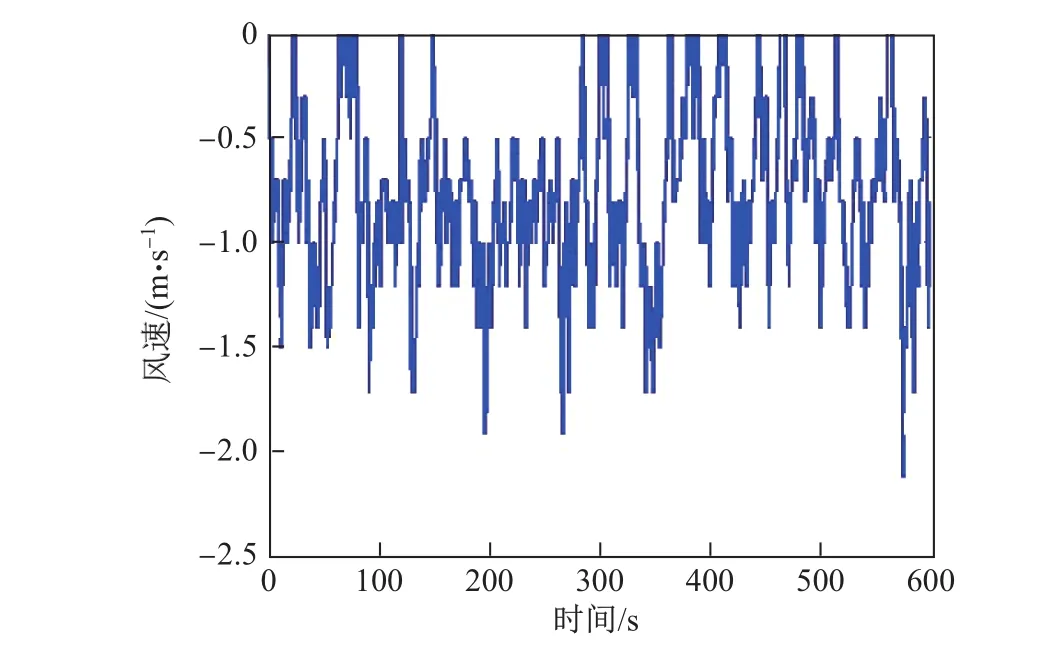
图5 隧道实验风速实测结果F ig.5 W ind speed experiment results in the tunnel

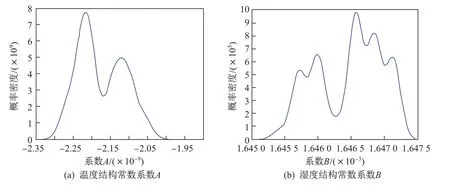
图6 温湿度结构常数系数的概率密度比较F ig.6 Comparisons of the coeffi cients of temperate and humidity structure constant

根据实测的10 min数据,结合式(5),(11),(12),(17),分别绘出折射率结构函数中三个相加项随时间变化的曲线(见图7).从图7可以更加明显地看到,在数量级的对比上,第三项远大于第二项2ABCTQ,更远大于第一项因此,可以得到本实验环境中对折射率结构常数影响由大至小的排序如下:湿度项>温湿掺混项>温度项.

由图8可知,在这个隧道水平风的环境下,大气折射率结构常数的取值大约为3×10-14,和Nessel等[16]在Goldstone,CA地区实验得到的结果在数量级上一致.

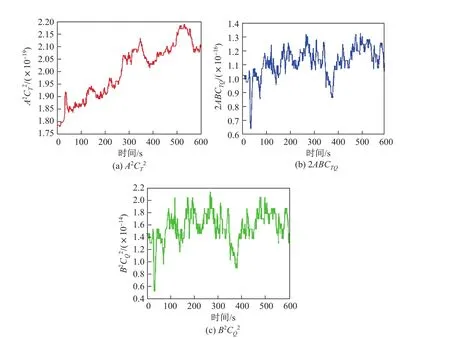
图7 大气折射率结构常数相加项的比较F ig.7 Comparisons of the additions of the atmospheric refractive index structure constant

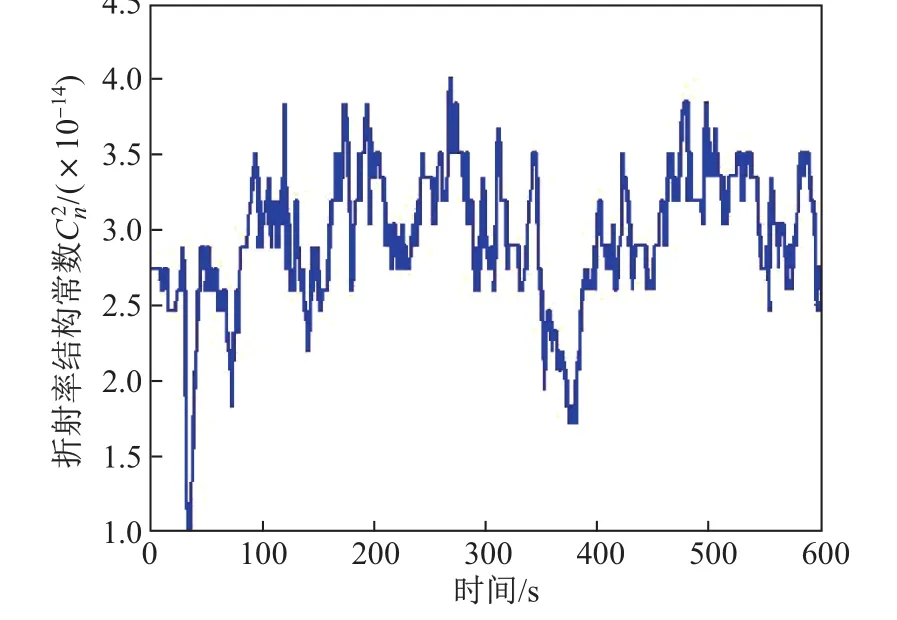
图8 大气折射率结构常数Fig.8 Atmospheric refractive index structure constant

3 结束语

本工作把空气中的水蒸气作为影响微波段折射率结构常数的重要因素,也是造成光波段和微波段折射率结构常数差异的主要原因.把空气划分成无水蒸气无CO2的空气、CO2、水蒸气三部分,重点研究了水蒸气对折射率的影响,导出了温度结构常数系数A和湿度结构常数系数B.温度结构常数C2T、湿度结构常数C2Q和温湿度掺混结构函数CTQ是仅与两点间温湿度的脉动有关的量,而与传输的波的频率无关.本工作选择TKE闭合方案计算温湿度结构常数,建立了温湿度结构常数与耗散率的关系.最后结合以上两个结论建立了微波折射率结构常数的模型,并利用相似性原理,在水平气流环境下将上述模型运用在水平坐标上.结合所建立的模型,分析实测数据可以发现,在本工作的实验环境下,2.4 GHz微波段的C2n取值大约为3×10-14,湿度对微波的折射率结构常数的贡献远远大于温度.

[1]张永静,赵东东.基于FLUENT测轨道交通隧道中电波折射率结构常数[J].上海大学学报(自然科学版),2014,20(3):458-465.

[2]Q U H,H U J,G AO X.The impact of Reynolds number on two-dimensional aerodynamic airfoil flow[C]//World Non-Grid-Connected W ind Power and Energy Conference.2009:1-4.

[3]T HIERMANN V,L OHSE H,E NGLISCH G.Modeling optical turbulence in the atmospheric boundary layer over sea[C]//Satellite Remote SensingⅢ.1997:198-203.

[4]H UTT D L.Modeling and measurements of atmospheric optical turbulence over land[J].Society of Photo-Optical Instrumentation Engineer,1999,38(8):1288-1295.

[5]ITU-R.On propagation data and prediction methods required for the design of space-to-earth and earth-to-space optical communication systems[S].Geneva:ITU-R,2007.

[6]C HEINET S,S IEBESMAAP.The impact of boundary layer turbulence on optical propagation[C]//Remote Sensing.2007:67470A-67470A-12.

[7]MARONGAB,D INTHER D V,MOENE A,et al.Derivation of turbulent structure parameters fromlarge-eddy simu lations and comparison with large-aperture scintillometer data and aircraft observations[J].Journal of the Atmospheric Sciences,2012,71:716-733.

[8]E DGAR L A.Estimatingover snow and sea ice frommeteorological data[J].Wave Propagation,1988,5(4):481-495.

[9]D EICHL K.Der brechungsindex f¨ur licht und mikrowellen[J].Allgemeine Vermessungs-Nachrichten,1984,91(3):85-100.

[10]E SSEN L,F ROOME K D.The refractive indices and dielectric constants of air and its principal constituents at 24 000 Mc/s[J].Proceedings of the Physical Society:Section B,1951,64(10): 862.

[11]B ARRELL H,S EARS J E.The refraction and dispersion of air for the visib le spectrum[J].Philosophical Transactions of the Royal Society of London,Series A,Mathematical and Physical Sciences,1939,238(786):1-64.

[12]C HEINET S,C UMIN P.Local structure parameters of temperature and humidity in the entrainment-drying convective boundary layer:a large-eddy simulation analysis[J].Journal of Applied Meteorology and C limatology,2011,50(2):472-481.

[13]H EUS T,V AN H EERWAARDEN C C,J ONKER H J J,et al.Formu lation of the Dutch atmospheric large-eddy simu lation(DALES)and overview of its applications[J].Geoscientific Model Development,2010,3(2):415-444.

[14]MOENG C H.Alarge-eddy-simulation model for the study of planetary boundary-layer turbulence[J].Journal of the Atmospheric Sciences,1984,41(13):2052-2062.

[15]W YNGAARD J C,I ZUMI Y,C OLLINS J R,et al.Behavior of the refractive-index-structure parameter near the ground[J].JOSA,1971,61(12):1646-1650.

[16]N ESSEL J A,MANNING R M.Derivation ofmicrowave refractive index structure constant(C2n) of the atmosphere fromK-band interferometric phasemeasurements[J].IEEE Transactions on Antennas&Propagation,2014,62(11):5590-5598.

Modeling atmospheric refractive index structu re constan t ofmicrow ave in horizontal airfl ow

CANG Lei1,2,ZHAO Hengkai1,2,ZHENG Guoxin1,2
(1.School of Communication and In formation Engineering,Shanghai University, Shanghai 200444,China; 2.K ey Laboratory of Specialty Fiber Optics and Optical Access Networks,Shanghai University, Shanghai 200072,China)

Electromagnetic waves propagating in the atmosphere are infl uenced by atmospheric turbulence.The structure constant of atmospheric refractive index are generally used to describe turbu lence intensity.This paper studies eff ects of the water vapor pressure in air on atmospheric refractive index in the 2.4 GHzmicrowave band.Aturbu lence kinetic energy(TKE)closure scheme is chosen and the structure constant of temperate and humidity is calcu lated with a turbulent dissipation rate.Then the normalization formulas for dry air are revised at themicrowave frequency of 2.4 GHz,and amodel of the structure constant of atmospheric refractive index is built in the microwave band in a horizontal airfl ow.In addition,the model is applied to calculate the atmospheric refractive index structure constant ofmicrowave based on themeteorological parameter actually measured in a tunnel environment.The result indicates that humidity has amore obvious eff ect on refractive index structure constant in the 2.4 GHzmicrowave band than temperature.

refractive index structure constant;microwave;horizontal airfl ow;vapor pressure

TN 925

A

1007-2861(2017)04-0501-09

DO I:10.12066/j.issn.1007-2861.1715

2015-09-02

国家自然科学基金资助项目(61271061,61171086);上海大学创新基金资助项目(SDCX 2012064)

赵恒凯(1968—),男,副教授,博士,研究方向为无线通信、电波传播等.

E-mail:hkzhao@staff.shu.edu.cn