基于模糊变结构动态贝叶斯网的目标识别方法

高晓利，李 捷,2

(1.四川九洲电器集团有限责任公司，四川 绵阳 621000；2.电子科技大学 通信抗干扰国家重点实验室，四川 成都 611731)

基于模糊变结构动态贝叶斯网的目标识别方法

高晓利1，李 捷1,2

(1.四川九洲电器集团有限责任公司，四川 绵阳 621000；2.电子科技大学 通信抗干扰国家重点实验室，四川 成都 611731)

在研究分析各信源信息的特征和目标识别的基本流程的基础上，基于传统静态贝叶斯网络，提出了一种基于模糊变结构动态贝叶斯网络的目标识别方法。该方法构建了模糊变结构动态贝叶斯网络，并提出了基于样本信息的统计方法和无样本的贝叶斯网络参数学习方法，以期网络推理实现目标属性识别，并在传统硬判决的基础上，实现了基于软判决准则的动态判决和基于线性加权思想的网络参数在线更新。数值实验表明，相对于传统静态贝叶斯网络目标识别方法，所提出的方法能够解决不同时刻证据的时序关系问题以及不能处理连续随机变量推理的问题，提高了目标识别置信度，缩短了识别收敛周期，能够有效纠正关联错误和关联多义性所造成的错误识别问题，解决了网络参数一成不变的问题，较好地实现了网络参数的在线更新。

数据融合；目标识别；贝叶斯网络；结构学习；参数学习

0 引 言

目标识别是电子信息系统不可或缺的一项重要功能，通常是指在发现目标的基础上，通过问答、信号分析、数据融合、情报印证等方式，生成目标类型、种类乃至身份信息。有效的目标识别是形成清晰准确的战场态势的基本要素之一，是指挥员正确决策和准确高效地指挥作战行动、武器系统准确选择打击目标的重要前提，对于提升基于信息系统的体系能力、避免误伤具有重要意义[1]。

贝叶斯网络理论在目标识别、数据挖掘、人工智能等处理不确定问题方面具有其特有的优点，能够处理不确定性和概率性的事件与事物，能够用于学习因果或其他类型的关系，是一种将专家知识与数据进行综合的理想表达模式。其模型灵活性好，能自然地将专家知识融入模型中，具有令人瞩目的从数据中导出模型的能力，并能继续用专家知识和数据改善模型的性能，而且它的模型结构和参数具有明确的含义[2-6]。

然而，传统基于贝叶斯网络的目标识别方法有些许不足：没有充分考虑到不同时刻间的证据时序关系；网络结构基本保持不变，与实际情况不符；参数在识别过程中没有实现在线更新。另外，传统贝叶斯网络模型只能解决离散随机变量的推理问题，而不能解决连续变量随机变量的推理问题[7-15]。

在研究时刻证据的时序关系、模糊数学理论的基础上，提出了基于模糊变结构动态贝叶斯网络的目标识别方法。该方法充分考虑了不同时刻证据的时序关系，构建的模糊变结构动态贝叶斯网络结构更符合实际情况，并且实现了目标识别的动态判决和参数的在线更新，解决了传统方法不能处理连续随机变量的推理问题。

1 预备知识

定义1：目标识别指通过对目标信息特征进行分析、鉴别，从而对目标类型、属性做出判断。

定义2：贝叶斯网络[13]BN=(G,θ)，其中G=(V,E)是一个非循环有向图，简称为DAG，θ是一个条件概率分布集，θi∈θ表示在给定节点Xi的父节点时Xi的条件概率，节点集V的联合概率分布表示为：

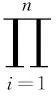
(1)

其中，Pai表示节点Xi在G中的父节点集。

(2)

2 基于模糊变结构动态贝叶斯网络的目标识别方法

首先构建模糊变结构动态贝叶斯网络架构，然后基于专家知识和数据库，完成网络参数的离线学习和制定，进而完成目标识别，最后实现目标属性的动态判决和参数在线更新。如图1所示，可分为五个阶段：

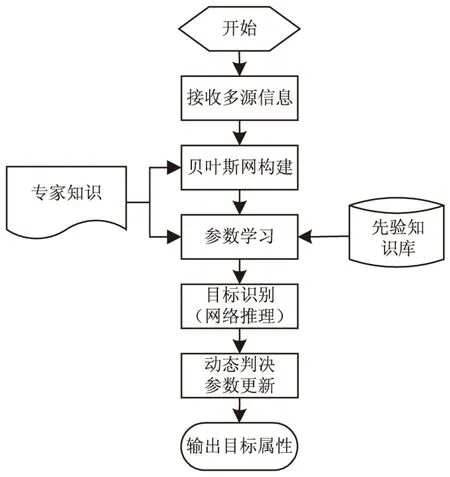
图1 基于贝叶斯理论的目标识别流程

2.1模糊变结构动态贝叶斯网络的构建

假设载机能够获取目标的识别信息、辐射源信息和运动信息三大类用于目标识别的多源信息，其中识别信息有应答和无应答两种状态；辐射源信息包含载频、重频、脉宽三类信息，其状态均是连续值；动态信息包含距离、方位、航速、航向以及高度五类信息，其状态均是连续值。针对模糊连续随机变量，基于模糊理论和分段思想，实现连续变量的离散化，离散化后目标识别信息状态取值如下：

在随机变量离散化的基础上，根据不同时间片证据之间以及证据与目标属性之间的关系，构建多源信息目标识别的变结构动态贝叶斯网络(见图2)，该网络可以根据实时接收的数据和证据进行适当裁剪[15]。

2.2参数学习

目标识别网络参数先验分布和先验条件概率可分为基于样本信息的统计方法和无样本信息的方法，其详细过程如下：

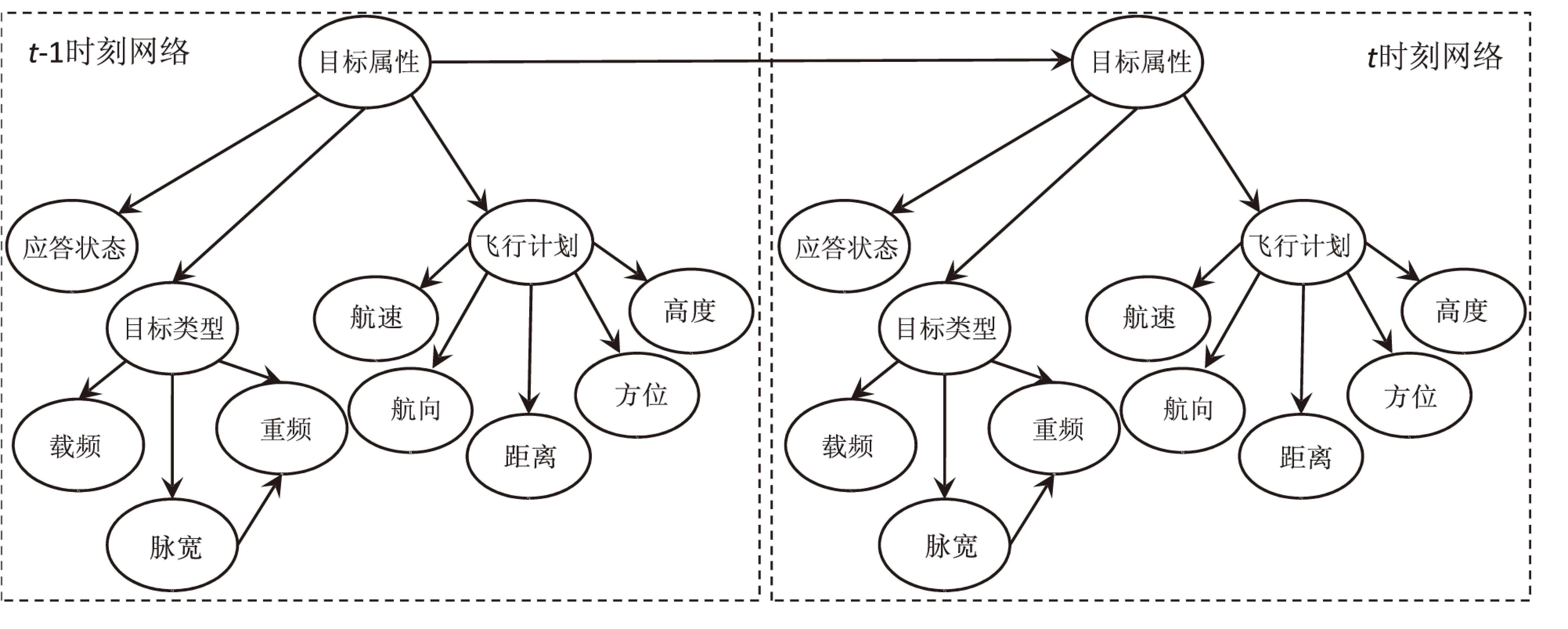
图2 变结构动态贝叶斯目标识别网络

(1)基于样本信息的统计方法。

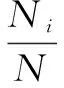
(2)无样本信息的方法。

如果目标型号为θ1平台，那么重频为高、中、低的可能性分别为0.6、0.3、0.1；如果目标型号为θ2平台，那么重频为高、中、低的可能性分别为0.1、0.3、0.6；如果目标型号为θ3平台，那么重频为高、中、低的可能性分别为0.333、0.333、0.333；如果目标型号为θ4平台，那么重频为高、中、低的可能性分别为0.333、0.333、0.333；如果目标型号为θ5平台，那么重频为高、中、低的可能性分别为0.333、0.333、0.333。

2.3目标识别

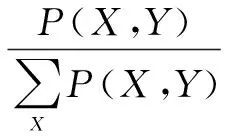
(3)

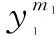
(4)

结合[1,t-1]时间段内目标属性集{θn1[1],…,θnt-1[t-1]}，θni[i]∈{θ1,…,θ5}，融合[1,t]所有时刻的结果，得到目标属性为θ的后验概率为：

P(θ|θn1[1],θn1[2],…,θnt[t])=

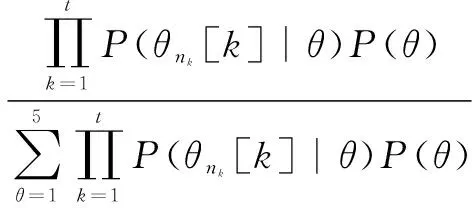
(5)

至此，得到变结构动态贝叶斯网络目标识别融合结果。

2.4动态判决

(6)

因此，为了解决硬判决造成的目标识别错误问题，提出了基于软判决的目标识别方法。

假设FVDBN融合出的目标五种属性所对应的后验概率中，最大概率和第二大概率所对应的属性分别为θi和θj，那么对于给定的门限ε，如果满足Pi>εiPi-Pj>ε，则输出目标属性θi，否则，暂时不输出目标属性或判断目标属性为不明。

2.5参数在线更新

基于目标识别结果，利用线性加权方法完善先验概率和先验条件概率，以先验分布概率更新为例进行说明。

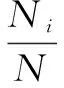
PNew(θi)=ωprior*P(θi)+(1-ωprior)*Pi

(7)

ωprior+(1-ωprior)=1

(8)

3 仿真实验

3.1场景描述

为验证基于模糊变结构动态贝叶斯网络的目标识别方法的性能，构建了一个由4个平台构成的场景，其中3个属性为θ2的目标，编号分别为11、12和23，1个属性为θ1目标，编号为82，如图3所示。

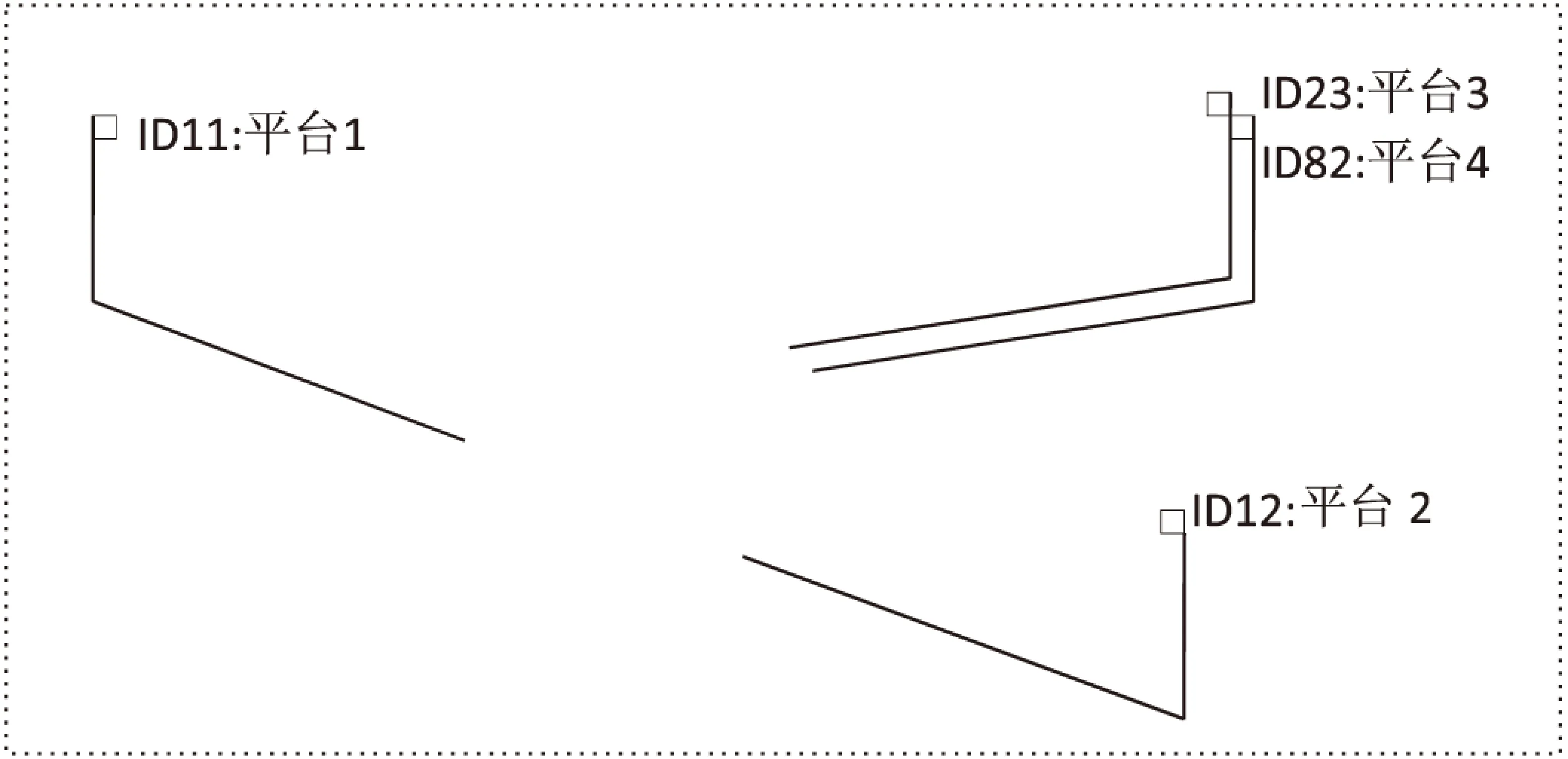
图3 场景设置示意图

场景描述：由识别主体11负责对某海域进行监视支援，属性为θ2的23号目标与属性为θ1的82号目标互相监视。同时属性为θ2的目标12在执行完侦查任务后返航。

3.2仿真结果

仿真条件：识别主体作为融合中心能够接收目标的识别信息、辐射源信息和动态信息，仿真周期为41，下面从识别信息指向是否一致两方面进行仿真。

3.2.1 识别信息指向一致

在以11号识别主体为视角的场景中，12号目标与其他目标之间的相对位置差别较大，因此，不会出现关联错误的情况，且该目标的所有识别信息指向均一致。

经典BN方法和FVDBN方法仿真结果如图4所示。

图4 12号目标识别结果对比

由图4可见，传统BN方法虽能够推断出目标的正确属性，但是直至第10个周期才达到收敛门限，而基于FVDBN方法不仅能正确推断出属性为θ2的高置信度识别结果，并且在第4个周期已经达到收敛门限。因此，FVDBN方法相对于BN方法，充分利用了不同时刻证据间的时序关系，不仅能够提高目标识别的置信度，而且能够缩短识别收敛周期。

3.2.2 识别信息指向不一致

当目标分布比较密集时，很可能出现识别信息指向不一致的情形，如从图3中可以看出，23号、82号目标与识别主体11的相对位置异常接近。

识别主体11对23号目标进行询问，获取应答状态后进行数据关联处理，把应答标志错误关联到82号目标上，此时，对传感器1提出请求，同时结合82号目标有无应答状态进行目标属性识别。经典BN方法和FVDBN方法关于23号目标和82号目标的仿真结果如图5和图6所示。

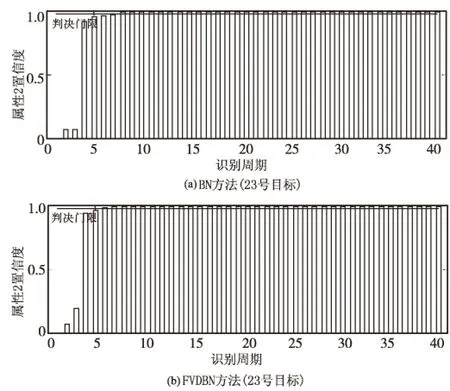
图5 23号目标识别结果对比

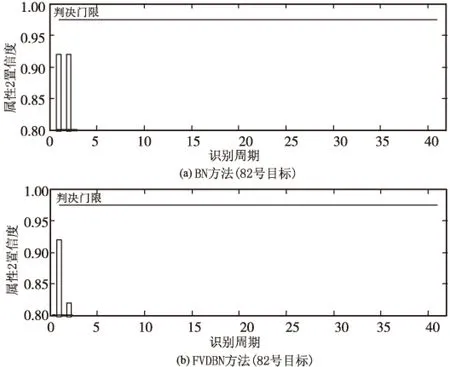
图6 82号目标识别结果对比

结合图5和图6可知，相对于经典BN方法，FVDBN方法在第2个周期对23号目标识别结果指向属性θ2的置信度较大，同时对82号目标识别结果指向θ2的置信度较小，进而82号目标指向属性θ1的置信度就较大，降低了错误识别的可能性。通过动态判决得到目标属性的同时，可以利用式(7)实现贝叶斯网络参数的在线更新，并实时保存至先验数据库，有效解决了网络参数一成不变的问题。

4 结束语

针对模糊变结构动态贝叶斯网络的目标识别方法，在充分研究不同时刻证据间关系和连续随机变量取值离散化问题的基础上，提出了基于样本信息的统计方法和无样本的贝叶斯网络参数学习方法，并在传统硬判决的基础上，实现了基于软判决准则的动态判决和基于线性加权思想的网络参数在线更新。该方法相对于传统静态贝叶斯网络目标识别方法，能够提高目标识别置信度、缩短识别周期，解决由关联错误造成的识别错误问题，同时能够实现贝叶斯网络参数的在线更新。

[1] 何 友， 王国宏， 关 欣，等.信息融合理论及应用[M].北京：电子工业出版社，2010.

[2] Huang Shuai, Li Jing, Ye Jieping,et al. A sparse structure learning algorithm for Gaussian Bayesian network identification from high-dimensional data[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(6):1328-1342.

[3] Yao J Y,Li Jiao,Li Hongzhi,et al.Modeling system based on fuzzy dynamic Bayesian network for fault diagnosis and reliability prediction[C]//Annual reliability and maintainability symposium.[s.l.]:[s.n.],2015:1-6.

[4] Zhou He, Hu Jiang, Khatri S P,et al.GPU acceleration for Bayesian control of Markovian genetic regulatory networks[C]//2016 IEEE-EMBS international conference on biomedical and health informatics.[s.l.]:IEEE,2016:304-307.

[5] Bouchaala L,Masmoudi A,Gargouri F,et al.Improving algorithms for structure learning in Bayesian networks using a new implicit score[J].Expert Systems with Applications,2010,37(7):5470-5475.

[6] Bui A T,Jun C H.Learning Bayesian network structure using Markov blanket decomposition[J].Pattern Recognition Letters,2012,33(16):2134-2140.

[7] Li Shuohao, Zhang Jun, Sun Boliang,et al.An incremental structure learning approach for Bayesian network[C]//Proceedings of the 26th Chinese control and decision conference.[s.l.]:[s.n.],2014:4817-4822.

[8] Yan Zhiyong,Xu Congfu,Pan Yunhe.Improving naive Bayes classifier by dividing its decision regions[J].Comput & Electron,2011,12(8):647-657.

[9] Neapolitan R E.Learning Bayesian networks[M].[s.l.]:[s.n.],2002:40-43.

[10] Chickering D M.A transformational characterization of equivalent Bayesian network structures[C]//Proceedings of the eleventh conference on uncertainty in artificial intelligence.San Francisco:Morgan Kaufmann,1995:87-98.

[11] 崔博鑫，许蕴山，向建军，等.一种基于异类传感器信息融合的目标识别方法[J].计算机工程与应用,2012,48(24):113-116.

[12] Zhou Yun,Fenton N,Neil M.Bayesian network approach to multinomial parameter learning using data and expert judgments[J].International Journal of Approximate Reasoning,2014,55(5):1252-1268.

[13] Ibrahim W,Beiu V.Using Bayesian networks to accurately calculate the reliability of complementary metal oxide semiconductor gates[J].IEEE Transactions on Reliability,2011,60(3):538-549.

[14] 于俊伟，刘 楠，张德贤，等.反舰导弹类型识别的贝叶斯网络方法[J].计算机工程与应用,2012,48(9):215-217.

[15] 周 毅，胡锡健.动态贝叶斯网络在战争身份识别中的应用[J].山西师范大学学报:自然科学版,2014,28(3):9-13.

A Target Identification Method of Dynamic Bayesian Network with Fuzzy Variable Structure

GAO Xiao-li1，LI Jie1,2

(1.Sichuan Jiuzhou Electronic Group Co.,Ltd.,Mianyang 621000,China;2.National Key Laboratory of Science and Technology on Communications,University of Electronic Science andTechnology of China,Chengdu 611731,China)

By researching and analyzing the characteristics of the source information and the basic process of target identification,on the basis of traditional static Bayesian network,a method of target identification based on fuzzy variable structure dynamic Bayesian network is proposed.It constructs the fuzzy variable structure dynamic Bayesian network and proposes a statistical method based on sample information and a learning method of sample-free Bayesian network parameters for implementation of target identification according to network inference and application of traditional hard decision.The dynamic decision has been performed based on the soft decision principles and the network parameters’ update online is finished based on liner weighting theory.Compared with traditional static Bayesian network for target identification, it has solved the issues such as the sequential relationship of evidence at different time and the networks inference of constant random variables.Meanwhile it has not only improved the confidence coefficient of target identification but also shortened the identification convergence period and effectively resolved error identification problem caused by error or ambiguity association.In addition,the problem of network parameters unchanged has been solved and the network parameters’ update online has also been completed.

data fusion;target identification;Bayesian network;structure learning;parameter learning

2016-10-09

：2017-01-13 < class="emphasis_bold">网络出版时间

时间：2017-07-05

国防预先研究项目(12100201)

高晓利(1983-)，女，工程师，硕士研究生，研究方向为目标跟踪、数据融合、数据关联、贝叶斯网络等。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170705.1652.082.html

TP274

:A

:1673-629X(2017)09-0017-05

10.3969/j.issn.1673-629X.2017.09.004