基于OpenCL的RNA二级结构预测算法

汪方良，施慧彬

(南京航空航天大学 计算机科学与技术学院，江苏 南京 211100)

基于OpenCL的RNA二级结构预测算法

汪方良，施慧彬

(南京航空航天大学 计算机科学与技术学院，江苏 南京 211100)

包含假结的RNA二级结构预测在计算分子生物学中一直是一个重要的研究领域，而预测包含任意类型假结结构已被证明为NP完全问题。为了解决此类问题，在CPU平台上实现了一种改进的遗传算法。该算法可预测包含两类假结结构的RNA序列，敏感性可达到0.775，阳性预测率可达到0.822 5。针对基于遗传算法带假结的RNA二级结构预测低效的问题，提出了基于OpenCL的异构并行加速算法。该算法在分析串行算法并行性的基础上，在种群迭代进化阶段进行异构加速，并基于GPU设备和OpenCL编程框架改进算法过程。为验证所提算法的可行性和有效性，基于相同的测试集进行了实验测试。测试结果表明，相对于串行算法，改进后的异构并行加速算法平均可实现2.72倍的速度提升，有效降低了RNA二级结构预测的耗时，提高了算法模拟预测效率。

RNA二级结构预测；假结；OpenCL；异构计算

0 引 言

RNA在基因表达中起到了十分重要的作用，对于每种RNA的功能分析，解析其结构特征是关键的一步。通过实验方法分析RNA结构特征虽然精确，但成本较高，因此，通过计算方法预测RNA二级结构一直是近年来计算分子生物学领域比较热门的课题之一。

目前预测RNA结构的算法大致可分为两类：基于多序列比对的预测算法和单序列预测算法。多序列比对算法利用了同源RNA序列具有的相近遗传信息与结构特性，预测精度较高，但是需要较多的先验信息[1-2]。而单序列预测算法只需要输入目标序列的一级结构，就可以预测出对应的二级结构且能保证一定的精确度。其中广泛应用的算法思想是基于最小自由能(Minimum Free Energy,MFE)的二级结构预测。1999年，Zuker等提出用动态规划算法(Dynamic Programming)计算各类环区自由能之和，从而预测一个单链RNA的二级结构[3]。在此基础上，国内外研究人员进行了大量探索。何静媛将人工鱼群算法运用到RNA二级结构预测中[4]；邢翀运用模拟退火算法[5]提高了结构预测的效率；Sato K等在MFE模型的基础上运用分割函数(Partition Function)进一步产生最大预期精度，进行二级结构预测[6]。但上述算法都没有包含RNA结构中一类重要的子结构—假结。包含任意假结的RNA二级结构预测已被证实为NP-complete问题[7]，目前大部分算法会对假结的类型进行限制，启发式算法在假结预测中效果较好。Ruan J等提出一种环匹配算法，不仅可以以单链作为输入，同时支持输入多条序列进行比对预测，从而提高精度[8]。类似的算法还有HotKnots[9]和FlexStem[10]，都是通过迭代添加子结构完成预测。Tong K K等提出了一种改进的遗传算法[11]。基于改进遗传算法中的三种遗传操作，实现了包含两类假结的RNA二级结构预测，并基于OpenCL实现了算法的并行加速，有效提高了结构预测的效率。

1 改进的遗传算法

1.1相关定义

首先定义遗传算法中的基因、染色体、个体、种群与RNA二级结构中相关概念的映射关系。

定义1：RNA二级结构中的每个茎区(Stem)代表一个基因；多个茎区的集合组成染色体(Chromosome)；每个染色体代表一个个体(Individual)；个体的集合构成种群(Population)。

对于茎区的概念与定义参见文献[12]。改进后的遗传算法包括三种遗传操作。

定义2 交叉(Crossover)：在两个个体i,j之间，从i中随机选取一个茎区p，茎区p必须对个体j是有效茎区；从个体j中随机选取一个茎区q，茎区q对于个体i是有效茎区，如能在i,j中找到这样一对茎区p,q，则进行茎区交换。

假设有两个个体{3,2,6,1,4}与{4,5,8,0,2}，个体{3,2,6,1,4}代表该个体由5个茎区组成，从左至右代表茎区在构成个体时被添加的先后顺序。个体{3,2,6,1,4}与个体{4,5,8,0,2}进行交叉操作，交换了stem 1与stem 0得到个体{3,2,6,4,0}与个体{4,5,8,2,1}。一个茎区对于一个个体是有效的，称为有效茎区，在不包含假结预测的算法中，茎区不存在交叉与重叠则是有效的，而提出的算法包含了假结结构预测，允许茎区交叉(具体交叉的类型在假结类型中详细介绍)，允许茎区重叠两个碱基对。根据Mathew&Tuner的标准能量模型中的定义，茎区的碱基对越多，长度越长，则自由能越小，那么在MFE的算法思想下，自然会选择最长且没有重叠的茎区构成个体，但是目前已经有部分研究证明，最优结果往往不完全出现在自由能最小的个体中，而是一些自由能次小的个体[13]。因此采用的算法中允许两个碱基对的重叠存在，而当重叠发生后，后加入的茎区舍弃重叠区的碱基对，保留原有个体内茎区结构不变。

定义3 替换(Replacement)：从个体中随机选取一个茎区p，从茎区池中随机选取茎区q，如果茎区q对于该个体是有效茎区，则从该个体中剔除茎区p并加入茎区池，将茎区q从茎区池取出添加到个体中。

茎区池是在输入RNA序列后根据碱基配对原则生成的所有候选茎区的集合，茎区池的构建将在下文算法流程中详细介绍。需要注意的是，由于每个个体的进化都是独立的，所以每个个体将独立维护一个自有的茎区池。

定义4 添加(Addition)：从茎区池中随机选取一个茎区p，若茎区p对于该个体是有效的，则从茎区池取出添加到个体中。

定义5 适应度(Fitness)：以个体的自由能值作为适应度，自由能越小，适应度越高。自由能的计算公式如下：

E=Estem+Ehairpin+Ebulge+Einternal+Emultibranch+Epknots

(1)

其中，Estem表示个体中所有茎区能量值；Ehairpin表示所有发卡环能量值；Ebulge表示所有凸环能量值；Einternal表示所有内环能量值；Emultibranch表示所有多分支环能量值。

前五个类型的子结构能量值计算都按标准能量模型MT计算，但是MT模型中不包括假结的情况，因此对于假结的能量计算采用D&P09能量模型中假结的计算办法。对于前五个子结构的计算方法见文献[14]。支持的假结类型定义如下：

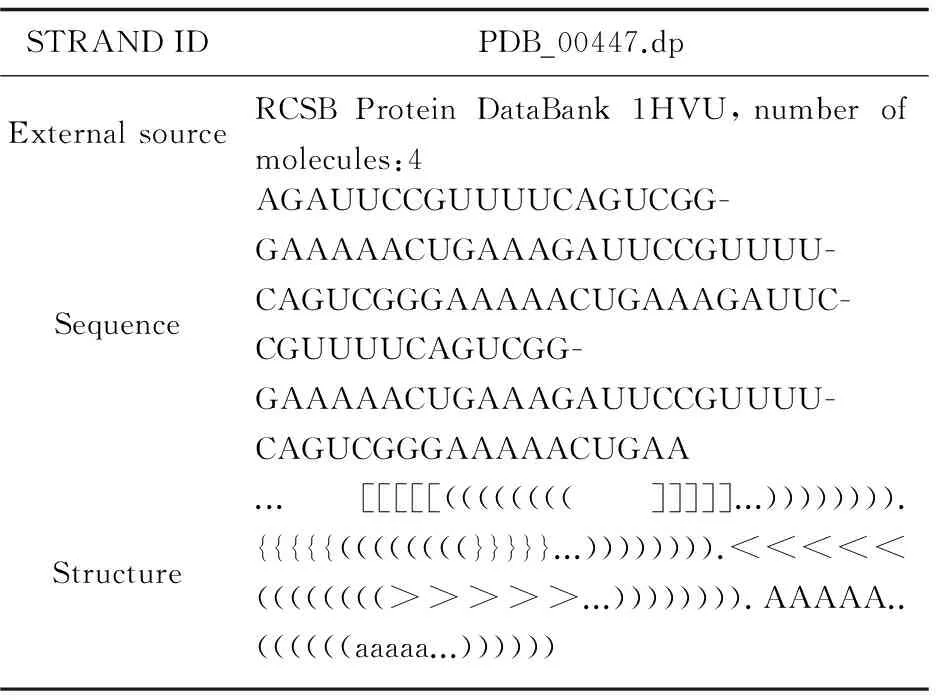
定义6 假结(Pseudoknots)：一个RNA的二级结构就是一组碱基对的集合，对于所有的碱基对，如果存在两对碱基对(i,j),(k,l)，其中i

RNA的假结结构有很多种，最常见的有H-type型假结[15]。提出的算法支持两种假结结构的预测：H-type型假结和多分支环内含有一个或多个H-type假结，如图1所示。

图中箭头左边为RNA序列起始端即5’端，右边带箭头的末端表示3’端[16-17]，两端之间的圆点表示碱基，弧线表示两端的碱基配对形成碱基对，相邻的配对碱基构成Stem。如图1(a)所示，H-type假结由两个茎区交叉形成，图1(b)中多分支环内包含一个H-type假结，提出的算法也支持包含多个H-type假结结构的预测。

图1 两类可预测假结结构

从公开RNA数据库RNA STRAND中搜索到这两种类型的真实RNA序列，见表1和表2。

表1 H-type假结序列

表2 多分支环包含假结序列

其中在Structure一行中，记录的是该RNA的真实二级结构，“.”表示未配对碱基，括号和字幕表示配对的碱基。将上述两个RNA序列作为输入，检测算法的有效性。

1.2算法步骤

(1)构建茎区池。

构建茎区池(StemList)的通常做法是根据碱基配对原则，找出所有可能的茎区，但实际上，很多长度较小的茎区并不会出现在真实的二级结构中。此外，穷举所有可能的茎区构成茎区池会增大算法搜索茎区的范围，增加算法的计算复杂度。文中算法采用最大茎区构建茎区池，所谓最大茎区就是指茎区池中只保留长度最大的茎区。比如有N对连续碱基对的茎区称为长度为N的茎区，则该情况包含N*(N-1)/2个子茎区，若只保留最大茎区(长度为N的茎区)，则可以大大缩小茎区池的容量，在文中算法采用的数据集中，运用最大茎区构建的茎区池是通常办法的1/3。

输入长度为n的RNA一级序列，先构造一个n*n的矩阵，矩阵的i行j列即代表第i个碱基与第j个碱基。若这对碱基满足Watson-Crick碱基配对原则(AU，GC)或者Wobble碱基配对原则(GU)，则矩阵中的(i,j)元素置1，否则置0。填充完矩阵所有元素后，以矩阵的下三角子矩阵为范围，沿着次对角线的方向，逐一寻找连续的值为1的元素序列，每个元素序列即是最大茎区，所有的最大茎区构成茎区池。

(2)初始化种群。

构建完茎区池后，将茎区池中的茎区按照自由能从小到大排序，初始化初代个体算法如下：

算法：初始化种群

输入：StemList

输出：初代种群

Set all stems being unused

for each Individual in population

for each Stem in StemList

if Stem is used before then

continue

end if

if Stem is valid for Individual

then

Create temporary individualtempid

tempid=Individual.addstem(Stem)

if tempid.energy

then

Individual=tempid

Stem is used

end if

end if

end for

end for

为了保持种群个体的多样性，在构造初始种群时，茎区池中的茎区每个只使用一次，这样就保证了初始种群中每个个体的基因都不一样。种群个体之间的差异性保证了种群进化的有效和健康。其次，在初始化初代种群时，每个个体都会维护一个自有的茎区池，比如自有茎区池当中有1～10，10个最大茎区，Individuali包含{2,3,5,7,9}五个茎区，那么其自有的茎区池则包含剩下的{1,4,6,8,10}五个茎区，自有茎区池在遗传操作中使用的方式已在定义2～4中介绍了。

(3)种群迭代进化。

完成种群的初始化后，以初始化种群为输入，进行迭代进化。对于种群中的所有个体，都会随机发生Crossover、Replacement、Addition三种遗传操作中的一个，即三种遗传操作是等概率(1/3)发生。其次，在迭代进化过程中，常见的遗传算法会设置迭代次数，文中算法设置了监视周期，监视周期之后，会监视种群内所有个体，如果个体的自由能不再发生变化，则结束迭代。监视周期设置为20轮迭代。迭代次数超过监视周期，并且种群内所有个体自由能不再降低，即是种群迭代进化停止的条件。算法步骤如下：

算法：种群迭代进化算法

输入：初始化种群

输出：进化完成的最优种群

While halting condition do not meet do

for each Individualiin population

Prob=rand()%100

Create 2 temporary individualt1,t2

if Prob<=crossover rate then

Randomly pick an individuala,wherea!=i

t1=Individuali,t2=Individuala

Crossover(t1,t2)

Ift2.energy

Individuala=t2

end if

else if Prob>crossover rate AND Prob<=replacement rate then

t1=Individuali

Replacement(t1)

else if Prob>replacement rate AND Prob<=addition rate then

t1=Individuali

Addition(t1)

end if

ift1.energy

Individuali=t1

end if

end for

end while

上述算法中，自由能即每个个体的适应度，计算方法如定义5，三种遗传操作如定义2～4。当种群迭代进化完成后，输出最终的种群个体，按照自由能由小到大进行排序，考虑到最优解有可能出现在能量次小的个体中，此处输出自由能最小的5个个体，并考量算法预测的精确度。

1.3预测结果评估

目前较为流行的评估办法主要从两个维度进行测算：敏感性(Sensitivity)和阳性预测率(Positive Predictive Value)[18]，其公式如下：

(2)

(3)

其中，TP表示正确预测的碱基对数；FP表示错误预测的碱基对数；FN表示真实结构中应该存在但是预测结果中未能预测的碱基对数。

目前较为著名的开源软件及算法，比如RNAfold、CentroidFold、ILM、HotKnots、pknotsRG等平均的敏感性在0.5～0.75之间，阳性预测率在0.65～0.75之间。

预测首先实现了一种改进的遗传算法，预测包含两种假结的RNA二级结构，但是在预测中，尤其是包含假结的预测，计算复杂度较高，耗时较长，而遗传算法本身具有一定的可并行性，因此运用异构并行计算对上述算法进行改进和提升。

2 基于OpenCL的并行加速

2.1OpenCL简介

OpenCL(Open Computing Language)即开放计算语言，是非盈利技术联盟Khronos Group管理的异构编程框架。其主要作用是将异构设备用于并行算法加速，具有较好的跨平台性。与技术特征类似的CUDA相比，OpenCL支持更多种类的加速设备，比如FPGA，DSP，CPU，GPU(包括部分移动端设备)。OpenCL能够将不同架构的设备整合到统一框架下，释放加速设备的计算性能，为通用计算提供更多的计算资源，提高计算效率。

OpenCL架构包含四种模型的定义：平台模型、执行模型、内存模型、编程模型。平台模型定义了异构平台、加速设备、主设备、计算单元之间的关系；执行模型定义了内核(kernel)如何在设备上执行，以及如何配置执行内核所需的上下文等环境；内存模型定义了一个抽象的内存分层，可以保证开发人员无需关心底层的内存架构；编程模型定义了并发模型与物理硬件之间的映射关系。关于OpenCL的详细内容参见文献[19-21]。

2.2OpenCL执行步骤

(1)获取可用的平台信息；

(2)获取可用的设备列表(GPU/CPU)；

(3)为加速设备创建上下文；

(4)为加速设备创建命令队列，以便宿主机向加速设备发送各类命令；

(5)创建程序(program)对象，编译内核代码；

(6)创建内核对象，关联内核代码；

(7)设置内核参数；

(8)执行内核函数；

(9)读取执行结果。

从上述流程可以发现，OpenCL程序最主要的部分在于kernel的设计与实现。针对需要加速的算法如何提取可并行部分，用kernel代替，在加速设备上实现并行运行是算法改进的关键。

2.3并行遗传算法

对于一个算法的并行化改进，可以有两种思路：任务并行、数据并行。任务并行是指，算法的两个任务阶段的输入输出不存在依赖关系，可以独立执行，那么就可以安排两个任务并行计算；数据并行是指，前后两次计算的指令相同，只是输入的数据不同。在上述介绍的改进遗传算法中，可以发现种群中的每个个体的进化实际上是独立自主的，并不一定需要等待其他个体进化完成，所以所有个体进化可以看作任务并行进行改进。其次，每个个体的遗传操作(交叉、替换、添加)都是三种之一，只是输入的数据不同，因此可以看作数据并行进行改进。算法流程如图2所示。

图2 并行遗传算法

工作项(Work item)是OpenCL平台模型中定义的最小计算单元，工作项最终会和加速设备上的计算核心相互映射。比如GPU平台就有数千个计算核心，并行遗传算法为大小为n的种群分配n个工作项，每个工作项独立负责该个体的遗传操作。这里的遗传操作即是定义2～4中的过程。

但是三种遗传操作中，交叉操作在并行情况下，有可能引起冲突：当个体a与个体b同时选中个体c(a、b、c互不相等)进行交叉操作时，即会引起冲突，导致畸形的后代。在提出算法中，畸形的后代体现为无效的茎区被保存在二级结构中，这样的结果并不是所需要的，所以在每轮迭代后，并行算法会进行畸形后代的筛选，舍弃错误无效的输出。通过实验发现，这样确实会带来部分性能的损失，但是从单轮测试数据来看，每一百个个体中会产生五个左右的畸形后代，损失在可接受范围以内。

对于健康的后代根据自由能的大小进行判断，如果自由能小于父代，则用子代代替父代个体进入下一轮遗传操作；如果子代自由能比父代大，则舍弃，仍由父代进入下一轮遗传操作，直至迭代超出监视周期(20轮)，且所有个体的自由能都不再减小，则结束遗传操作，进化完成。输出自由能最小的五个个体。

3 实验及结果分析

3.1有效性测试

为了测试算法的通用性，实验数据不仅包括含假结的RNA序列，同时包括不含假结的RNA序列。实验测试源数据来自RNA STRAND公开数据库。测试长度在43～125 nt之间。预测结果对比见图3。图中，(a)、(c)、(e)是来自数据库的RNA序列真实二级结构，(b)、(d)、(f)是所提算法预测结果通过RNA Movies软件输出的平面二级结构。其中(a)是RFA_00730号RNA序列，(c)、(e)是表1、表2当中定义的序列。

图3 包含二级结构预测结果对比

从图中可以看出，不含假结及单个H-type假结序列的预测准确率较高，而包含多个H-type假结组成多分支环的序列相较前两种序列，准确度有所下降。从RNA的真实结构分析，多假结的结构复杂度更高，并且(e)的真实结构用目前的能量模型进行度量，并不是自由能最小的结构，也就是说多假结结构序列的最优解往往不在能量最小的情况，唯有进一步优化能量模型，才能提高多假结结构的预测准确率。综合测试数据集，所提算法平均阳性预测率达到0.822 5，平均敏感性达到0.775。说明该算法有效，预测结果有一定的参考价值。

3.2并行算法加速测试

(1)硬件环境：AMD A10-7400P 2.5-3.4 GHz，集成显卡AMD Radeon R6 Graphic，独立显卡 AMD Radeon R9 M280X，可用内存6.94 GB。

(2)软件环境：Windows 8.1(64bit)，驱动版本Catalyst 15.7，Visual Studio Ultimate 2012，AMD APP SDK 3.0。

以表2中的PDB_00447号序列为例，序列长度为120 nt，种群大小设置为300，监视周期为20，加速测试结果如图4所示。

图4 加速测试结果

如图4所示，该序列在140轮迭代后完成种群进化，以5轮迭代为间隔，对比了CPU(串行算法)和GPU(并行算法)的耗时。虽然在并行算法中，需要对因交叉冲突产生的畸形后代进行过滤，损失部分性能，但是从图中可以看出，并行算法相对串行算法仍有较大优势。从数据来看，平均加速比达到2.72x。

4 结束语

为了解决包含假结在内的RNA二级结构预测问题，提出并实现了一种改进的遗传算法。该算法能够预测包含两种假结结构在内的RNA二级结构。为了提升算法的预测效率，在保证预测结果有效的情况下，基于OpenCL对算法进行并行化改进与加速，平均获得2.72倍的速度提升，有效提高了算法的计算效率。但对于多假结结构的预测仍有提升空间，下一步工作是优化能量模型，提高多假结结构的预测精度。另外，并行算法每轮迭代之间有繁琐的内存传递过程，目前部分加速设备已经支持OpenCL 2.0中最新的共享虚拟内存(Shared Virtual Memory)，运用SVM技术优化访存过程，提升加速效果也是后续研究工作之一。

[1] 张涛涛.基于比较序列分析的RNA二级结构预测算法研究[D].哈尔滨：哈尔滨工业大学,2007.

[2] 方小永.基于比较序列分析的RNA二级结构预测与评估[D].长沙：国防科学技术大学,2007.

[3] Mathews D H,Sabina J,Zuker M,et al.Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure[J].Journal of Molecular Biology，1999,288(5):911-940.

[4] 何静媛.RNA二级结构预测算法的研究[D].重庆：重庆大学,2009.

[5] 邢 翀.RNA二级结构预测算法的研究[D].长春：吉林大学,2012.

[6] Sato K,Kato Y,Hamada M,et al.IPknot:fast and accurate prediction of RNA secondary structures with pseudoknots using integer programming[J].Bioinformatics，2011,27(13):85-93.

[7] Lyngso R B,Pedersen C N.RNA pseudoknot prediction in energy-based models[J].Journal of Computational Biology，2000,7(3-4):409-427.

[8] Ruan J,Stormo G D,Zhang W.An iterated loop matching approach to the prediction of RNA secondary structures with pseudoknots[J].Bioinformatics,2004,20(1):58-66.

[9] Ren J,Rastegari B,Condon A,et al.HotKnots:heuristic prediction of RNA secondary structures including pseudoknots[J].RNA，2005,11(10):1494-1504.

[10] Chen X,He S M,Bu D,et al.FlexStem:improving predictions of RNA secondary structures with pseudoknots by reducing the search space[J].Bioinformatics，2008,24(18):1994-2001.

[11] Tong K K,Cheung K Y,Lee K H,et al.GAknot:RNA secondary structures prediction with pseudoknots using genetic algorithm[C]//IEEE symposium on computational intelligence in bioinformatics and computational biology.[s.l.]:IEEE,2013:136-142.

[12] 彭 政.带假结的RNA二级结构预测算法研究[D].长沙：湖南大学,2008.

[13] Staple D W,Butcher S E.Pseudoknots:RNA structures with diverse functions[J].Plos Biology,2005,3(6):213.

[14] Andronescu M S,Pop C,Condon A E.Improved free energy parameters for RNA pseudoknotted secondary structure prediction[J].RNA,2009,16(1):26-42.

[15] 胥 杰.基于混沌模拟退火的RNA二级结构预测的研究[D].成都：电子科技大学,2010.

[16] 刘元宁，张 浩，李 誌，等.RNA假结结构分析[J].吉林大学学报:工学版,2009,39(S1):265-269.

[17] 高世乐,丁克诠.含假结RNA二级结构类的图语法[J].计算机工程与应用,2008,44(2):23-25.

[18] 刘振栋.包含假结的RNA结构预测算法研究[D].济南：山东大学,2014.

[19] Gaster B.OpenCL异构计算[M].张云泉,张先轶,龙国平,等,译.第2版.北京：清华大学出版社,2012.

[20] 詹 云,赵新灿,谭同德.基于OpenCL的异构系统并行编程[J].计算机工程与设计,2012,33(11):4191-4195.

[21] 陈 钢，吴百锋.面向OpenCL模型的GPU性能优化[J].计算机辅助设计与图形学学报,2011,23(4):571-581.

Secondary Structure Prediction of RNA Based on OpenCL

WANG Fang-liang，SHI Hui-bin

(College of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 211100,China)

Predicting RNA secondary structure is an important field in computational molecular biology especially including pseudoknots.However,predicting RNA secondary structure with all kinds of pseudoknots has been proven to be an NP-complete problem.To solve it,an improved genetic algorithm is proposed in CPU platform,which can predict two kinds of pseudoknots.Its sensitivity can reach 0.775 and its positive predictive value can reach 0.822 5.The prediction of RNA secondary structure with pseudoknots based on genetic algorithm is inefficient.To solve it,an accelerated algorithm based on OpenCL is presented,which accelerates the period of individual evolution according to the analysis of parallelizability of serial prediction algorithm.Then the algorithm established with GPU based on OpenCL is promoted.The contrast experiments with the same test set have been conducted compared with other algorithms.The experimental results show that the improved heterogeneous parallel algorithm has acquired 2.72 times faster average operation rate than others,reducing the computing time effectively and improving the efficiency of prediction.

RNA secondary structure;pseudoknots;OpenCL;heterogeneous computing

2016-10-31

：2017-02-17 < class="emphasis_bold">网络出版时间

时间：2017-07-11

国家“973”重点基础研究发展计划项目(2014CB744900)

汪方良(1991-)，男，硕士研究生，研究方向为异构计算、计算机体系结构；施慧彬，博士，副教授，研究方向为计算机体系结构、可重构计算。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170711.1456.078.html

TP311

:A

:1673-629X(2017)09-0001-06

10.3969/j.issn.1673-629X.2017.09.001