基于INNER -DBSCAN和功率曲线模型的风机异常状态检测
陈警钰, 陈玉航
(1. 东北电力大学 电气工程学院,吉林 吉林 132012;2. 国网山东电力公司 潍坊供电公司, 山东 潍坊 261021)
基于INNER -DBSCAN和功率曲线模型的风机异常状态检测
陈警钰1, 陈玉航2
(1. 东北电力大学 电气工程学院,吉林 吉林 132012;2. 国网山东电力公司 潍坊供电公司, 山东 潍坊 261021)
针对目前风电机组异常运行状态无法快速检测问题,提出一种基于INNER-DBSCAN算法和功率曲线模型的数据驱动实时检测方法。该方法先利用贝茨理论和RC模型构造一个新的约束来进行数据预处理,剔除机组极端异常运行数据;再基于提出的区间DBSCAN算法对数据进行聚类,得到正常数据和异常数据;最后利用区间邻域最值对正常数据进行边缘识别,构造风电机组正常运行时的功率曲线模型,并通过模式图的上下临界值识别风机异常运行状态。利用8台风电机组SCADA数据进行实验,结果表明,该方法能有效实时检测风机异常运行状态。
风电机组; INNER-DBSCAN; 实时检测; 异常运行; 功率曲线模型
0 引言
风电是最有前景的可再生能源之一,截至2014年底,中国的新增装机达到23 GW,风电机组累计装机容量已接近114 GW,Global Wind Energy Council(GWEC)对未来5年全球风电发展预测显示,未来5年内风电将继续保持增长势头[1]。然而由于风机运行天气环境(如严寒、酷暑、沙尘、降雪等)的多变性及严酷性,使得风机经常忍受快速变化的负载而产生的高强度机械应力,这导致风机平均寿命3%的时间都处于异常运行状态[2]。其运行维护费用能占到风电项目能源成本的10%~20%,在风机服役期的后期能达到35%,这样的大开销阻碍了风电更为快速的发展[3]。风机的异常运行状态检测在基于风机运行状态的维护和维修中起到了重要的作用,这比矫正性维护和预防性维护的性价比更高,能够大大地减少风机的运行维护费用[4]。
传统的风机异常状态检测专注于风机昂贵组成部件(如主轴、发电机、齿轮箱等)的故障识别,2个常用的方法是振动分析和油液检测,但这2个方法是独立的系统,需要安装额外的传感器和其他硬件设备[5]。而利用基于SCADA系统在风机控制器所采集的数据来提早预警故障和运行问题是性价比很高的方式[6]。
文献[7]提出通过风机的功率特性来检测其整体健康状态,并通过选择正常运行风机的数据来构建内部警戒线和外部警戒线,根据内外警戒线阈值去检测风机异常状态;文献[8]提出用制造商提供的功率曲线及经验值模型剔除异常数据,并分别用线性与非线性方法建立风机功率曲线模型;文献[9]提出利用基于四分位法和k-means算法的数据剔除模型来识别异常状态。然而由于不同风机、不同时间段的实测功率曲线不同,异常运行数据的分布也有所不同,此类方法通用性不高、异常状态检测准确度低。
文献[10]提出基于最小二乘法、最大似然估计方法和k-NN算法构建功率曲线模型,然后基于统计值得到功率曲线带,以此识别异常运行状态;文献[11]提出基于模型的风机状态检测,分别用线性、状态依赖参数模型(SDPM)、人工神经网络(ANN)进行建立,根据最优输出和预测值的残差去识别异常状态。上述研究中都有一个缺点是需要大量的训练过程,计算开销大,运行效率低下,很难应用在实时检测中。
DBSCAN算法是一种基于密度的数据分类方法,执行效率较高,可以识别多个簇。本文利用这个算法的思想提出了一个基于INNER-DBSCAN和功率曲线模型的风机异常状态检测方法,并进行了多风电场、多机型的实验测试。结果表明,该算法能够有效快速地识别出风机异常运行状态,可以对风电机组整体运行状态进行实时检测。
1 异常数据的特征及其对功率曲线的影响
风电机组功率特性一般用风电机组输出功率随风速的变化曲线即功率曲线(P-V)来表示,根据能量守恒定律及贝茨理论,得到风机实际能得到的有功功率,由公式(1)计算[12]:
P=0.5ρπR2Cpv3
(1)
式中:P是风机风轮捕获的理论功率;ρ为空气密度;R为用来确定扫略面积的风轮半径(叶片长度);v为风速;Cp为风能利用系数,它代表了控制系统利用风能的效率。
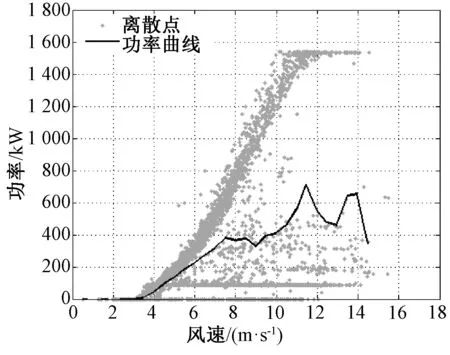
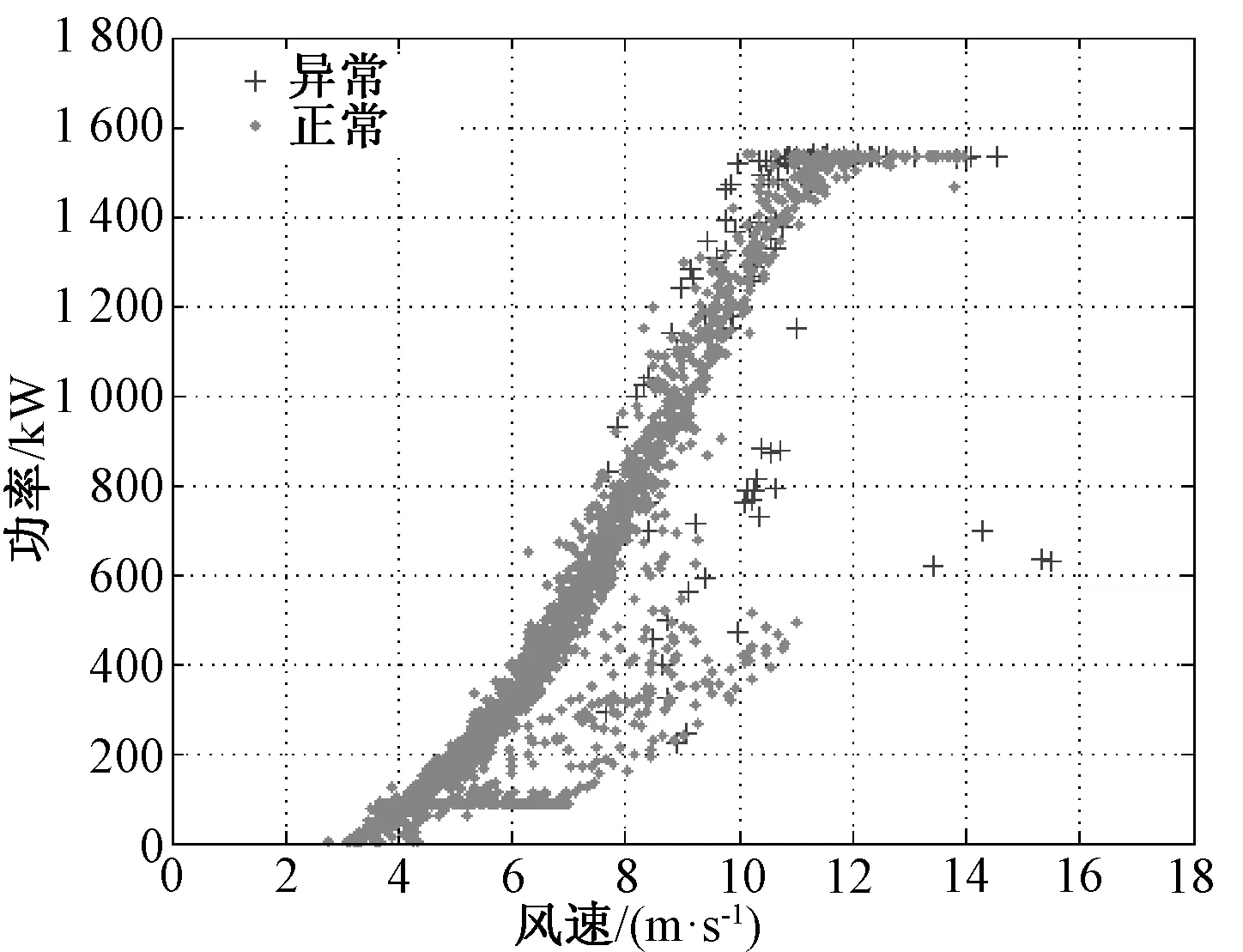
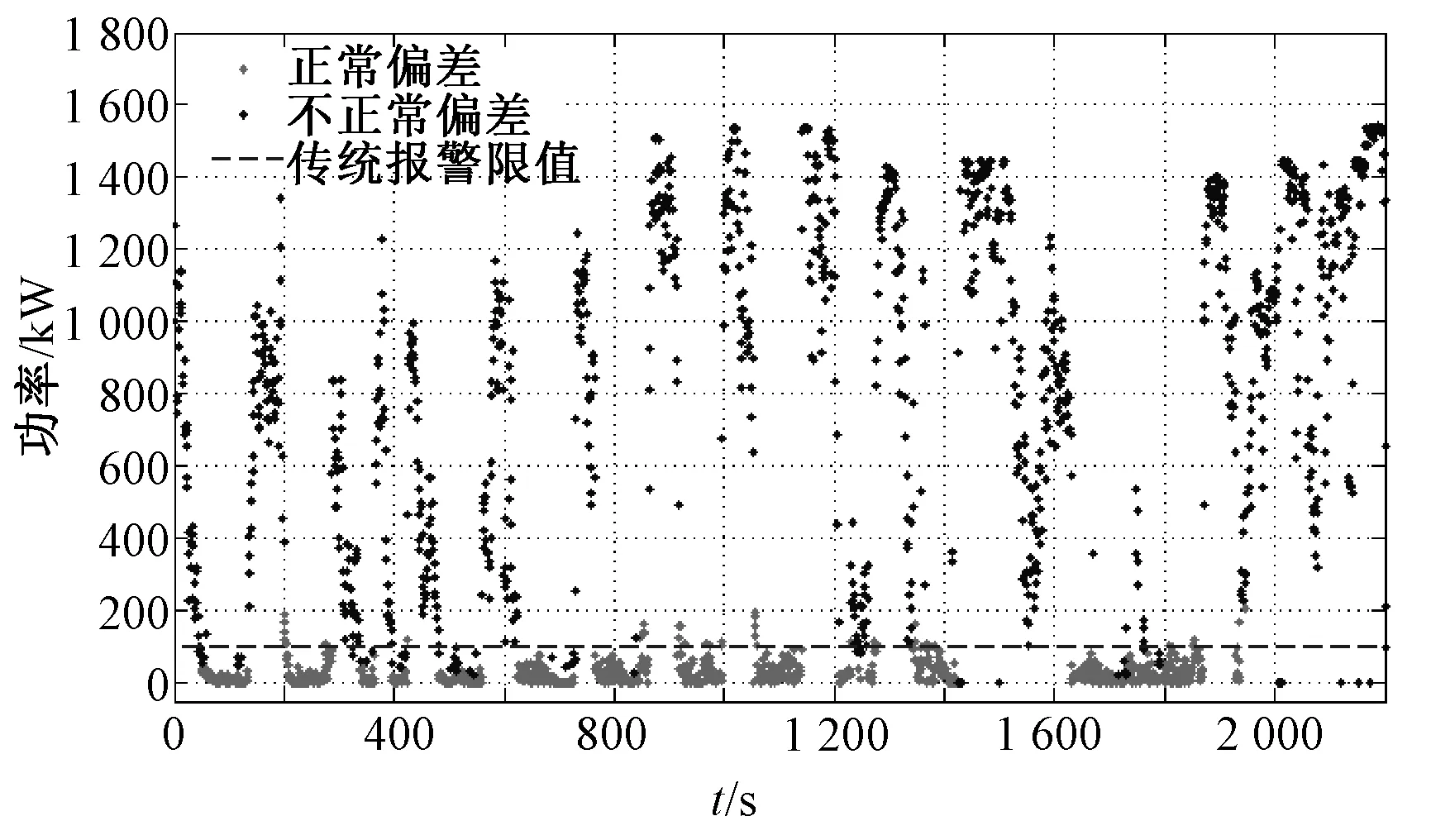
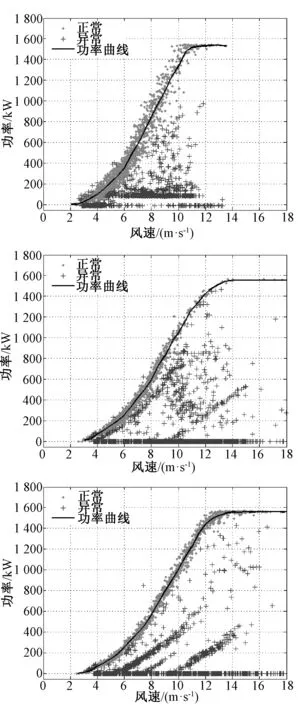
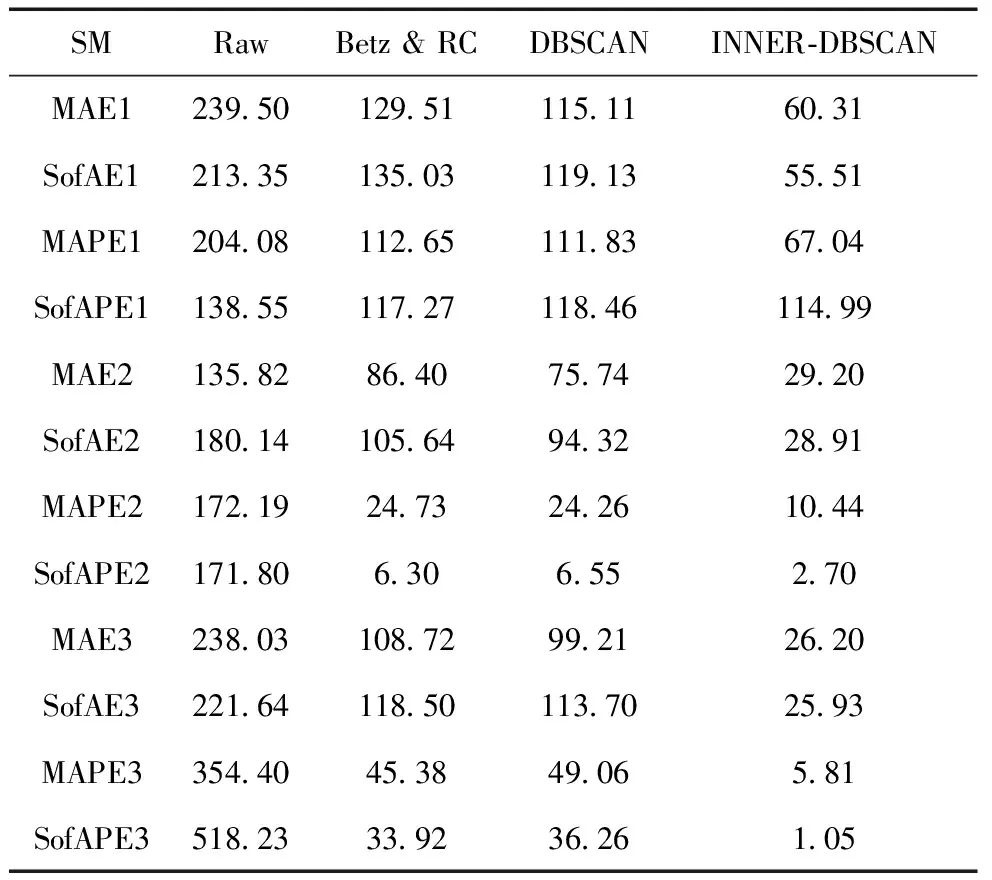
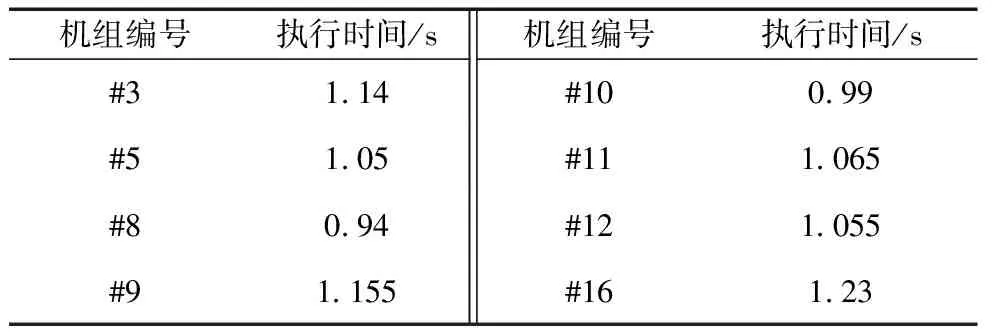
异常数据在本质上是机组故障以及机组缺乏维护而导致的停机或低性能运行现象;或者是风机处于正常运行情况下,而电力调度机构要求部分风电场降出力或暂停运行的现象。为了分析风机的功率性能,利用SCADA系统采集的数据进行分析。图1是某风机在某日4∶48至次日1∶00的风速和功率时序图,时间间隔为10 min。其切入风速为vi=2.5 m/s,额定风速为vr=11 m/s,vo=20 m/s,额定功率为1 500 kW。图1中,在4∶48 图1 风速和功率的时序图 把上述情形的时间轴延长,采集1个月的风机10 min数据,得到数据集U。正常运行数据与异常运行数据、停机数据、随机误差数据和系统误差数据混合在一起,导致无法进行正常的功率曲线建模,如图2所示。 图2 风速与功率关系散点图 尽管通过公式(1)得到的风机功率曲线模型是明确的,但是由于机组的内在缺陷使得无法精确预测输出功率。首先,因为风机在设计时假定空气密度为常数;其次预测错误或设计参数误差会在v3中放大[13],因此每台风机正常运行的功率性能也是不尽相同的,所以直接使用风机厂商提供的功率曲线对异常进行状态检测是不合适的。需要基于每台风机的实际运行数据来进行功率曲线建模,为下一步的机组异常运行状态检测提供基础。 2.1数据预处理 2.1.1 功率最优化约束 风能利用系数由公式(2)进行计算: (2) 式中:S为风轮扫略面积;v为风速;P为风机功率。根据贝茨理论,风能利用系数Cp的极限值为0.593。基于这个理论,可以确定功率曲线的上限曲线,称为Betz曲线。 2.1.2 功率最低约束 根据R.Chedid提出的功率曲线模型(称之为RC模型)确定功率最低约束: (3) P=PW×Aw×effw (4) 式中:Aw为风轮扫略面积;effw为风机对风能的利用效率。令effw取一个较低的利用效率0.05,可得到风机最低功率约束的曲线,这条曲线称为RC曲线。 根据Betz曲线和RC曲线对风机原始数据集U进行预处理,剔除掉了机组极端异常运行数据,如图3所示,得到预处理的正常数据集Upre-normal和异常数据集Upre-abnormal。 2.2INNER-DBSCAN算法 2.2.1 算法的提出 DBSCAN算法是由Martin Ester等人在1996年提出的著名的基于密度的聚类算法,它的优点是可以识别任何形状的簇和孤立点,这符合风机风速-功率散点的分布特点[14]。DBSCAN算法根据给定的密度阈值识别一个簇,密度阈值由Eps和Minpts2个参数决定(其中Eps表示半径,Minpts表示核心点在Eps半径范围内至少应该含有的点的数量)。 DBSCAN算法的参数Eps用经典的欧氏距离进行计算: (5) 聚类的中心即为各元素的均值由公式(6)进行计算: (6) 式中:m为第j个聚类所包含的数据对象的个数。 用4个统计学指标[15]来判定聚类结果,如公式(7)~(10)所示: (7) SDofAE= (8) (9) SDofAPE= (10) DBSCAN有一个比较明显的弱点,即当数据分布不均匀时,由于使用统一的全局变量,使得聚类的效果变差。以预处理之后的正常数据集Upre-normal进行聚类,聚类效果如图4所示(Minpts=5,Eps=0.327 1)。图4反映出某些风机的实际运行情况,可知当风机的风速-功率数据分布不均时,用统一的Minpts及Eps聚类得到的效果极差。结合DBSCAN算法的优点及风速-功率散点的分布特性,下面提出基于区间法的DBSCAN算法——INNER-DBSCAN算法。 图4 DBSCAN聚类结果 2.2.2 算法具体实现过程 利用区间法将风机运行数据的风速属性进行分区间,在每个小区间中利用DBSCAN算法进行聚类。 (1)将待分类的数据集按照风速0.5 m/s间隔分成若干个小区间。每个小区间中心值为0.5 m/s的整数倍,得到每个小区间数据集Ui为: (11) 式中:Ui为第i个区间的数据集;(v,p)为落在第i个区间的二维数据元素。假设Upre-normal最大风速为vmax,则最大风速区间为n=[vmax/0.5]。 (2)在每个小区间内利用DBSCAN算法聚类。DBSCAN算法基于一个事实,一个聚类可以由其中的任何核心对象唯一确定,即任一满足核心对象条件的数据对象p,数据库D中所有从p密度可达的数据对象O所组成的集合构成了一个完整的聚类且p属于C。数据集中没有包含在任何簇中的数据点就构成噪声点。 (3)正常簇判定及二次聚类融合。 在前面过程中,散点图的上方极端异常数据已经被剔除,因此最终期望保留的正常数据必然已经聚集在散点图的最上部分和最左部分,因此应尽可能地保留聚类结果中均值较大的聚类。 采用二次聚类融合思想:①对于上述风速区间,聚类结果为{C1,C2,…,Cm}或还有一个噪声簇N,计算这m个簇的聚类中心{w1,w2,…,wm};②找出{w1,w2,…,wm}中最大的聚类中心wmax,其对应的簇为Cmax初步判定为正常簇Cpre-normal;③计算wmax与{w1,w2,…,wm}中除wmax之外的各个聚类中心的聚类di=wmax-wi;④比较各个di与预设阈值T(如0.2Pr)的大小,如果di 对预处理后的正常数据Upre-normal按照INNER-DBSCAN算法进行聚类,每个小区间的聚类效果如图5所示。 图5 INNER-DBSCAN算法区间内聚类效果 图6 INNER-DBSCAN算法聚类效果 汇集每个小区间的聚类结果,得到整体的聚类效果如图6所示。很明显,INNER-DBSCAN聚类效果比单纯的DBSCAN聚类效果好得多,能够将绝大多数异常状态准确识别出来。但同时有部分正常点被误判为异常点(8.5 m/s左右及13 m/s左右)。下面介绍通过功率曲线模型进一步准确识别异常数据的方法。 3.1边缘识别 每个风速区间中,计算正常数据在风速均值邻近区间内的最大值和最小值,作为该区间内数据上下边界上的点。 第i个区间数据集Ui的风速均值为vmean,给定一个较小的邻近半径δ,在[vmean-δ,vmean+δ]内的数据集为Qi,计算出Qi最大功率pi,max和最小功率pi,min,即将点(vmean,pi,max)和点(vmean,pi,min)作为第i区间上下边界上的点。这样,由n个区间的n对上下边界点构成双S曲线的功率曲线模型,如图7所示。 3.2异常状态识别 根据功率曲线模型和线性插值算法判断任意数据点m(vj,pj)是否为异常运行状态,即判断vj对应的功率是否在功率曲线模型的上下边界之间[16]。 首先,利用公式(12)和公式(13)计算出功率曲线模型上下边界的每个小区间的斜率和偏移量: (12) (13) 对于任意一组实时数据(vj,pj),如vi<=vj (14) 同理,可以计算出vj对应的功率最小值plowest。如果plowest<=pj<=phighest,则该点为正常运行状态,否则为异常运行状态。根据功率曲线模型对原始数据重新分类,效果如图8所示。根据聚类得到的正常数据得到机组的功率曲线。 图8 基于功率曲线模型的重聚类 基于实测风速数据和上述功率曲线可以计算出理论功率,由理论功率和实测功率可以计算出功率残差。基于上述相同数据得到功率残差的时序图如图9所示。 图9 功率残差时序图 从图9可以看出,如果使用传统方法人为的设定一个功率残差限值,则会将一部分正常运行状态误认为是异常运行状态,也会将一部分异常运行状态误认为是正常运行状态。本文中提出的功率曲线模型方法能够根据机组正常运行状态自动调整上下限值,实现有效而准确地对异常运行状态识别。但是这个方法有时可能会引起过多的警报,解决的办法是根据需要在边缘识别步骤中设置上下限系数来扩大功率曲线模型范围。 为了验证本算法的有效性,本文采用8个风场的8台风机的实测风速-功率散点进行聚类结果分析。以其中3台风机为例,聚类效果图如图10所示,数据来源分别为A风场3#机组1月份数据、B风场12#机组5月份数据、C风场16#机组10月份数据。很明显,该方法能够准确识别机组异常运行状态。 图10 基于INNER-DBSCAN的聚类结果 造成3张图中异常状态的原因可能会有多种,像传感器故障、桨距角控制故障、不合适的叶片角度设置、叶片损坏、控制程序错误、限功率运行、环境条件问题(昆虫附着、脏物附着、叶片结冰)等。 3台风机的数据聚类统计指标表示的数据离散程度结果如表1所示。Raw指的是基于原始数据的分析结果,Betz&RC指的是经过Betz和RC曲线剔除极端异常数据后的数据集Upre-normal的分析结果,DBSCAN指的是在数据集Upre-normal基础上经过经典的DBSCAN算法得到的分析结果,INNER-DBSCAN指的是在数据集Upre-normal基础上经过本文提出的INNER-DBSCAN算法得到的分析结果。 表1 4个统计指标情形 很明显,从4种统计分析指标整体上来看,Raw的4项指标均为最大,表示数据离散度最大(即聚合度小);经过Betz & RC过程后数据聚合度变大;传统的DBSCAN不能明显地增加聚合度;而INNER-DBSCAN能够有效地增加数据聚合度。 以Betz & RC为基础,DBSCAN对3台风机的MAE指标平均降低了11%,而INNER-DBSCAN对MAE指标的平均降低指标为60%;DBSCAN对3台风机的MAPE指标平均降低了2%,而INNER-DBSCAN对MAPE指标的平均降低指标为62%。也就是经过INNER-DBSCAN算法后数据聚合度明显增大,结合图10来看,该方法对机组异常运行状态进行了有效的识别。 对本文提出的算法编写MATLAB程序,并在普通PC上运行。以8台机组单月数据为单位进行处理(经大量实验表明,以单月数据进行处理时聚类效果最好,数据量过多会造成聚类边界模糊,数据量过少会造成大量数据被误认为是噪声簇),聚类执行时间如表2所示,平均处理时间1.08 s,在处理速度快的服务器上运行,会进一步减少执行时间,实时应用性较高。 表2 INNER-DBSCAN 算法的执行时间 本文提出了基于INNER-DBSCAN算法和功率曲线模型的异常运行状态检测方法。基于Betz理论和RC曲线对数据进行预处理,大大地提高了数据聚类效果,对构建正确的功率曲线模型起到了很好的监督作用;利用DBSCAN算法基于密度聚类的优势,结合风机功率曲线散点的分布特点,提出在0.5 m/s小区间内应用的DBSCAN算法即INNER-DBSCAN算法,得到很好的聚类结果;基于区间平均风速邻域最值的方法能够有效识别机组正常运行数据的边缘,从而构造出功率曲线模型,利用功率曲线模型对原始数据进行重聚类,并采用4种数据聚类统计指标进行了分析,相对于数据预处理之后的数据聚合度提高了高达62%;该算法在普通PC上学习得到最终的功率曲线模型的执行速度较快,时间约为1.08 s,可以对功率曲线模型短时段更新,以对机组异常运行状态进行有效检测。该算法通用性高、计算开销小,风电机组功率状态检测具有理论研究和工程应用的价值。 [1] TCHAKOUA P, WAMKEUE R, OUHROUCHE M, et al. Wind turbine condition monitoring: State-of-the-art review, new trends, and future challenges [J]. Energies, 2014, 7(4): 2595-2630. [2] WALFORD C A. Wind turbine reliability: understanding and minimizing wind turbine operation and maintenance costs [J]. Journal of New Energy, 2016, 12(5):1129-1136. [3] CRABTREE C J, ZAPPALD, TAVNER P J. Survey of commercially available condition monitoring systems for wind turbines [J]. Supergen Wind, 2014, 40(5):90-98. [4] 马义松,武志刚. 基于Neo4j的电力大数据建模及分析[J]. 电工电能新技术, 2016, 35(2):24-30. [5] 肖峰,陈国初. 基于功率预测的含风电场电力系统经济优化调度研究[J]. 电力科学与工程, 2016, 16(10):9-14, 27. [6] SHOKRZADEH S, JOZANI M J, BIBEAU E. Wind turbine power curve modeling using advanced parametric and nonparametric methods [J]. IEEE Transactions on Sustainable Energy, 2014, 5(4): 1262-1269. [7] 赵永宁,叶林,朱倩雯. 风电场弃风异常数据簇的特征及处理方法[J]. 电力系统自动化, 2014, 21(1):39-46. [8] LONG H, WANG L, ZHANG Z, et al. Data-driven wind turbine power generation performance monitoring [J]. IEEE Transactions on Industrial Electronics,2015, 30(4): 356-364. [9] 李国栋,庞文杰,葛磊蛟,等. 基于改进雷达图法的光伏并网发电系统稳态电能质量综合评估[J]. 电工电能新技术,2016,35(5):8-12,35 [10] ZHANG Z, ZHOU Q, KUSIAK A. Optimization of wind power and its variability with a computational intelligence approach[J]. IEEE Transactions on Sustainable Energy, 2014, 5(1): 228-236. [11] 黄南天,袁翀,王新库,等. 基于互信息属性分析与极端学习机的超短期风速预测[J]. 电工电能新技术,2016,35(10):29-34. [12] 田增山,王向勇,周牧,等. 基于DBSCAN子空间匹配的蜂窝网室内指纹定位算法[J]. 电子与信息学报, 2017, 31(7): 1228-1237. [13] NAGARAJU S,KASHYAP M,MAHUA B. An effective density based approach to detect complex data clusters using notion of neighborhood difference[J]. International Journal of Automation and Computing, 2017,20(1):57-67. [14] 姜建华,杨玉免,边海燕,等. 改进DBSCAN聚类算法在电子商务网站评价中的应用[J]. 吉林大学学报(理学版),2016,15(2):329-336. [15] 邱强杰,陈众,俞晓鹏,等. 基于事件驱动控制理论的风力发电系统建模[J]. 电力科学与工程,2016,16(8):37-42. [16] 丁国辉,许莹南,郭军宏. 基于DBSCAN聚类算法的多模式匹配[J]. 计算机应用与软件,2016,56(2):25-29. Condition Monitoring for Wind Turbines Based on INNER-DBSCAN and Power Curve Pattern CHEN Jingyu1, CHEN Yuhang2 (1.School of Electrical Engineering, Northeast Dianli University, Jilin 132012, China;2. State Grid Weifang Power Supply Company, Weifang 261021, China) In the light of the problem of rarely an easy and effective way to monitor the abnormal operation status of wind turbine, a data driven abnormal real-time monitoring method for operation status based on INNER-DBSCAN algorithm and power curve pattern is put forward in this paper. A new constraint is developed by Betz’ theory and RC model to conduct data preprocessing so that the extremely abnormal operation data can be ruled out. Then interval DBSCAN algorithm is proposed for data clustering and hence both normal data and abnormal data could be obtained. Also, the maximum value of the interval neighborhood is utilized to recognize the edge normal operation data of wind turbine, and the power curve pattern is built based on it. Finally, the abnormal operation status is monitored by the upper and lower limit value of the pattern. The performance of the presented method is evaluated using SCADA data sets of eight wind turbines, and the results show this method could effectively monitor the abnormal operation status in real time. wind turbine; INNER-DBSCAN; real-time monitoring; abnormal operation; power curve pattern 2017-01-03。 10.3969/j.ISSN.1672-0792.2017.08.005 TM614 :A :1672-0792(2017)08-0027-08 陈警钰(1996-),女,硕士研究生,主要研究方向为电力系统安全性分析与控制。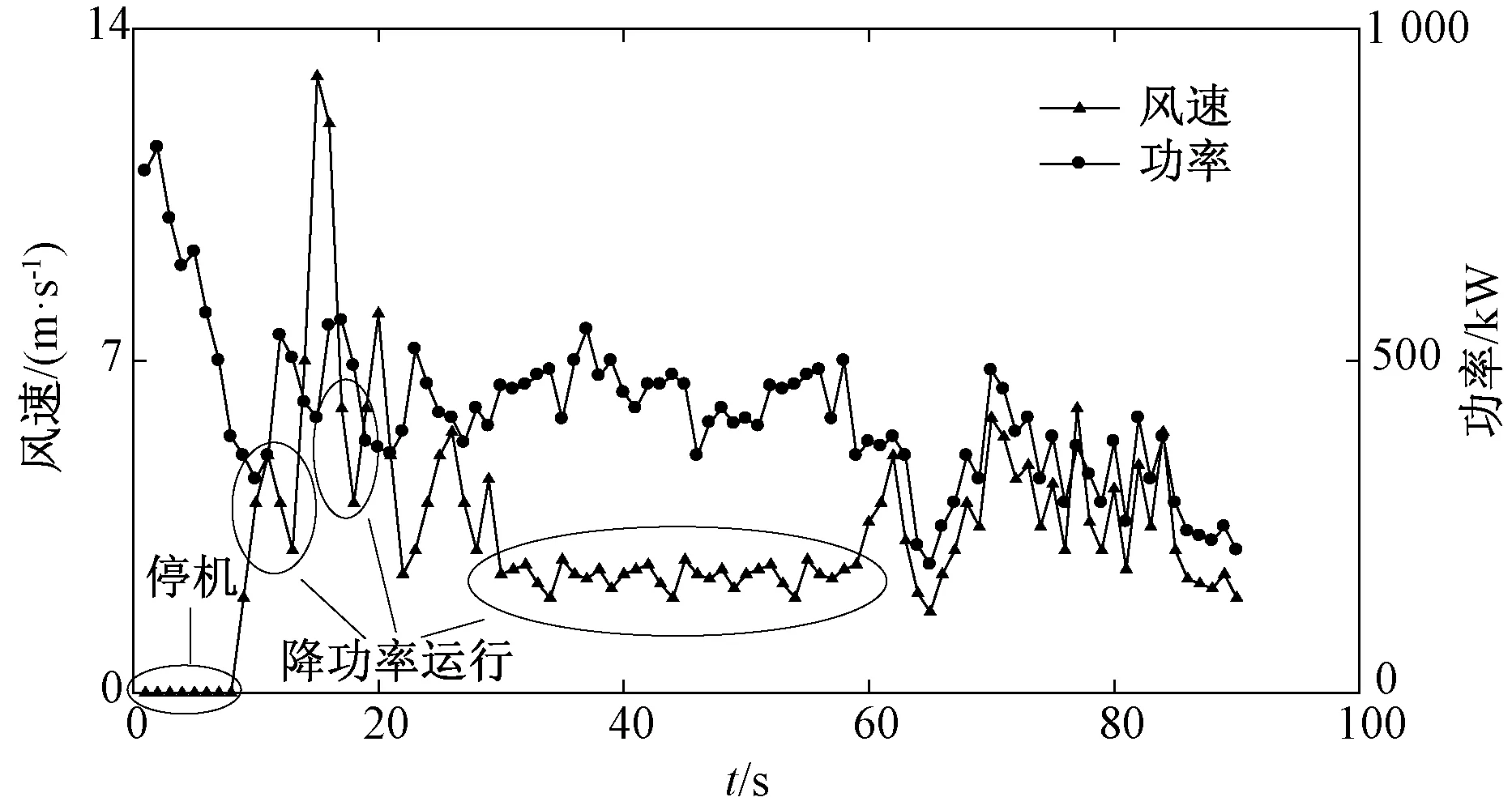
2 异常数据的识别原理及数学模型
3 功率曲线模型
4 工程实例
5 结论

