铺设角度与铺层顺序对层合板稳定性的影响

李根，吴锦武



铺设角度与铺层顺序对层合板稳定性的影响

李根，吴锦武

(南昌航空大学飞行器工程学院，江西南昌330063)

以层合板结构的临界屈曲载荷系数最大化为优化目标，基于改进型模拟退火算法对层合板结构铺设角度和铺层顺序进行优化。由于层合板结构的铺层角度是离散变量，模拟退火算法适合求解离散变量的优化问题。利用模拟退火算法优化层合板铺层，在算法内采用并行计算、引入记忆功能同时设置双阈值终止准则，有效地提高了优化过程的收敛速度，同时避免优化过程中出现局部最优解。以临界屈曲载荷系数作为目标函数，选取复合材料层合板的铺设角度顺序为设计变量，采用改进的模拟退火算法得出复合材料层合板的最优铺设角度以及铺层顺序。

模拟退火算法；临界屈曲载荷系数；铺层优化；层合板

0 引言

由于复合材料具有比强度高、比刚度大、比弹性模量高等性质，广泛应用于航空航天等结构的承载构件[1]。结构件的稳定性即屈曲问题是影响构件承载能力的决定性因素。因此研究复合材料层合板结构的稳定性至关重要[2]。

不同的铺设角度以及铺层顺序影响复合材料层合板结构的刚度，从而引起层合板结构的屈曲强度。近年来，以层合板稳定性为优化目标、铺设角度为设计变量的优化设计研究越来越多。如基于遗传算法和蚁群算法对层合板的屈曲进行了铺层优化[3-4]，多种算法相结合对层合板的稳定性结构优化[5-6]。上述研究成果中多数基于遗传算法、蚁群算法等进行优化分析，而模拟退火算法相比遗传算法等具有局部搜索能力强、运行时间较短等优点，已被越来越多的研究人员用于解决层合板的结构优化问题。如利用模拟退火算法并采用整数编码方式对层合板的屈曲载荷系数进行铺层优化[7]。Karakaya[8]等人计算了层合板的固有频率和临界屈曲载荷系数，然后将遗传算法与模拟退火算法相结合，以层合板的基频、屈曲为目标函数进行了铺层优化。Deng[9]等人分析了层合板的振动特性，然后利用模拟退火算法优化层合板的铺层厚度。Akbulut[10]等人在经典模拟退火算法的基础上对参数进行了适当调整，得到一种新型模拟退火算法并对层合板的铺层厚度进行了优化。

本文对经典模拟退火算法进行改进，解决搜索能力差等缺点，同时针对以临界屈曲载荷系数作为优化目标函数的经典模拟退火算法存在计算工作量大、计算效率偏低以及全局搜索目标函数等特点，选取复合材料层合板的铺设角度顺序作为设计变量，重点讨论不同的载荷比、不同长宽比以及不同铺层厚度时的最优铺设结果。

1 层合板稳定性分析

假设层合板受中面压缩与剪切载荷作用示意图如图1所示，其中和为层合板横截面上单位长度的内力(即拉力、压力或剪切力)，和为矩形层合板的长和宽。

层合板在偏离平衡状态下的屈曲平衡方程为[2]

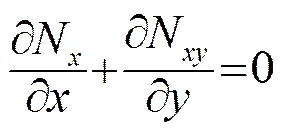
(2)

(3)

假设层合板为四边简支正交各向异性对称，其屈曲微分方程为

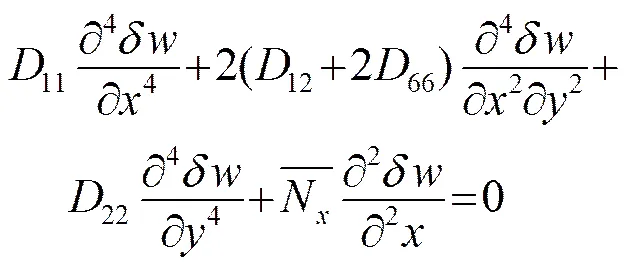
(5)

通过选取不同的和可得到一系列的值，其中最小的值即为层合板的临界屈曲载荷，显然当时有最小值，得到临界屈曲载荷为

(7)

式中，方向的屈曲半波数大小取决于层合板的刚度以及长宽比/的关系，根据最小值条件，求解下式：

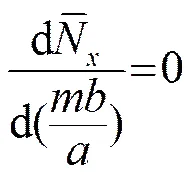
可得到：

(9)

将式(9)代入到式(7)中，可得：

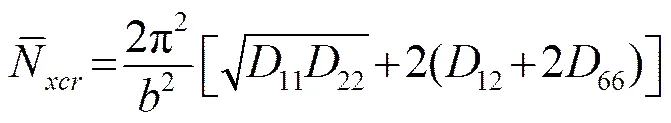
从式(9)可知：最小屈曲载荷对应长宽比/的整数倍。根据压杆稳定临界理论可知：个半波数与个半波数对应同一个临界屈曲载荷，即

(11)

求解得到：

(13)

当给定了长宽比和主弯曲刚度比，根据式(13)可判断出屈曲半波数。

如图2所示的层合板加载形式中，层合板四边分别受到和方向的均匀面内载荷和，其中是载荷因子，、是施加的载荷，且满足：，则当层合板发生屈曲时，相应的屈曲载荷系数为

(15)

2 模拟退火算法的改进

为了克服经典模拟退火算法的计算工作量大、计算效率偏低以及结果精度不高的缺点，本文对其算法进行如下改进：

(a) 将并行搜索的思想引入到模拟退火算法中来加快搜索速度。由于模拟退火算法是一种串行计算的优化算法，经典模拟退火算法在每一步循环中都会搜索当前状态下邻域中的随机点，从而大大增加了算法的运算量。为了解决这一问题，引入并行搜索的思想。

(b) 在算法的搜索过程中引入记忆功能。经典模拟退火算法中若想得到全局最优解，则需要同时满足初始温度足够高、温降过程足够缓慢并且在每一温度下进行的抽样较多，最终温度趋于零。但是全局收敛仍然较难以实现，并且通过接受概率得到的最优状态可能会比搜索轨迹中的某些其它中间状态还要差，导致最终得到的解和最优解偏差较大。所以为了不丢失目前的最好状态点并提高搜索效率，本文在算法的搜索过程中引入记忆功能，即在模拟退火算法的搜索过程中保留了期间最优解，并且随着搜索进程及时更新。

(c) 采用双阈值设置算法的内循环和外循环的终止准则，即在每一温度下的当前状态连续100次保持不变时则认为Metropolis抽样稳定，在温降过程中所得到的最优解连续10次温降都变化非常小时则认为算法收敛，此时终止计算输出结果。改进的模拟退火算法在尽量保持解的最优性的前提下减少了计算量，大大提高了效率。

3 层合板稳定性优化模型

将层合板的临界屈曲载荷系数作为目标函数，以层合板的铺设角度作为设计变量，层合板临界屈曲载荷系数最大化问题的数学模型为：

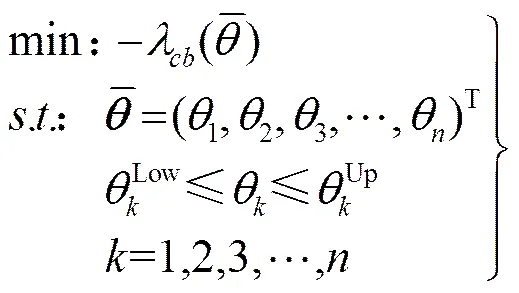
JLBS微小拉压力传感器采用了箔式应变片贴在合金钢弹性体上，承受拉、压力均可，具有测量精度高、稳定性能好、温度漂移小、输出对称性好、结构紧凑等特点。通过查阅技术手册，可以得到此压力传感器的综合精度为R=0.05%F·S，量程为M=25N。

4 数值分析

4.1 改进SA算法与经典SA算法的对比

首先用经典模拟退火算法(如图3所示)以临界屈曲载荷系数作为目标函数对层合板进行铺层角度优化，再利用改进的模拟退火算法对层合板进行铺层角度优化，通过对比两者的优化结果和迭代过程来分析改进后的模拟退火算法的优越性。

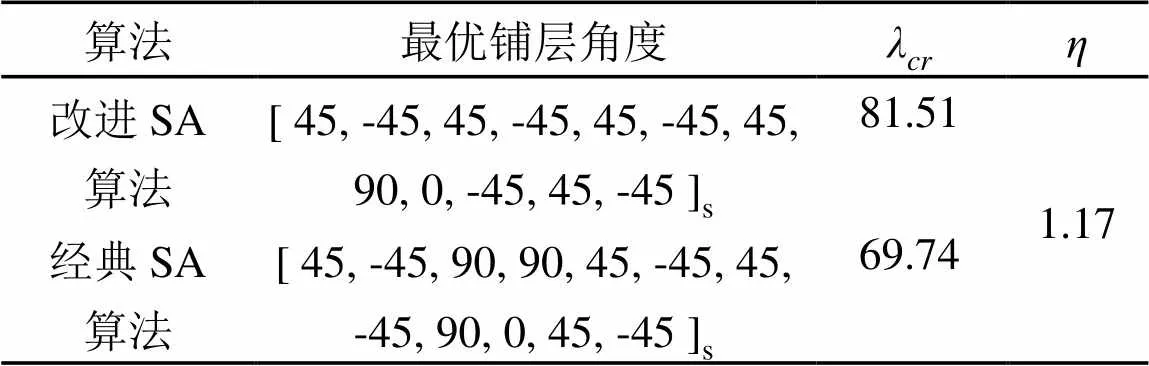
表1 x方向轴压时层合板优化结果对比

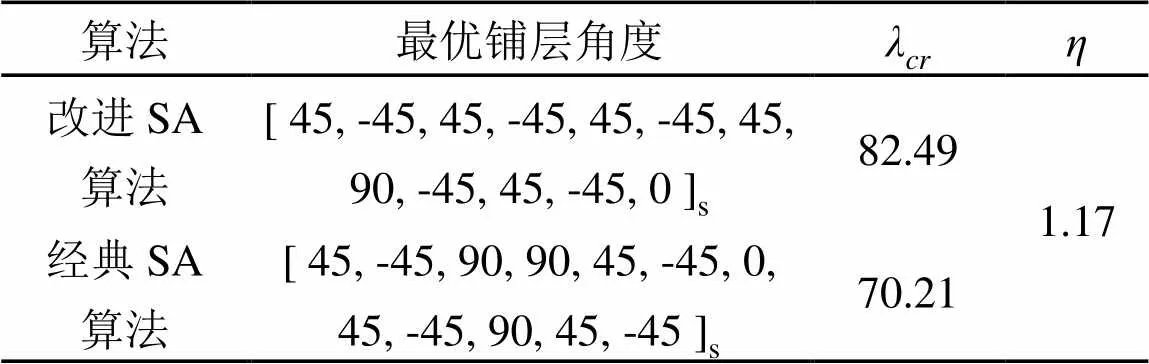
表2 y方向轴压时层合板优化结果对比

由表1和表2可知：和方向轴压时层合板最优铺层角度不同，同时改进后的算法的计算精度较经典算法要高17%左右，改进后的算法优化效果明显。

(a) 经典SA算法

(b) 改进SA算法

图4方向承受轴压时两算法的迭代过程

Fig.4 Iteration processes of two algorithms in thedirection of axial compression

(a) 经典SA算法

(b) 改进SA算法

图5方向承受轴压时两算法的迭代过程

Fig.5 Iteration processes of two algorithms in thedirection of axial compression

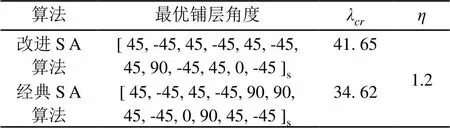
表3 x和y方向同时轴压时两算法优化对比

(a) 经典SA算法

由表3和图6可知：在和方向同时均施加载荷时，改进后的模拟退火算法在迭代过程中收敛效果较好，而经典算法由于没有引入记忆功能导致在迭代计算过程中出现了局部最优解，从而最终的优化结果精度比改进的算法低了20%左右。

4.2 不同载荷比时层合板的屈曲优化

从表4可知：对于不同的载荷比，层合板最后的铺层顺序也不同。随着载荷比增大，相应的临界屈曲载荷系越小。

表4 四边简支时层合板优化结果

(a)=0.125

(b)=0.15

(c)=0.20

(d)=1.00

图7 简支板不同载荷比时的迭代过程

Fig.7 Iteration processes of simple support plate with differentvalues

另外由图7可知：改进的算法收敛情况总体上较好。即当温度降到约为10 ℃左右时，算法开始趋于收敛，虽然之后仍会出现震荡情况但其幅度已非常小，最终当温度降到约为3 ℃时，算法终止并获得最优解。在迭代过程中，虽然改进的算法中引入了记忆功能，保留了每一温度下的最优解，但仍会出现目标函数值的震荡情况，主要是因为接受准则在邻域随机搜索时由于计算量大会造成搜索不均匀导致的局部最优解，但对最终的优化结果的影响不是很大，总体上较为满意。

4.3 不同长宽比时层合板的屈曲优化

以4.1节中的四边简支层合板为例，模拟退火算法初始温度参数，链长，指数退火衰减函数的温降速率系数，和方向承受均匀轴压。在不同长宽比时层合板铺层优化结果如表5～7所示。

由表5和表7可知：(1) 不同厚度的层合板在不同长宽比时，上下表层的纤维铺设方向变化不大；(2) 铺层越厚，层合板的临界屈曲载荷则越大；(3) 在边长比为1时，上表层铺设角度为±45°的铺层有利于提高临界屈曲载荷，而在边长比为1.5和2时，在层合板上表层连续铺设三层90°的铺层有利于提高临界屈曲载荷；(4) 相比文献[11]的遗传算法结果，改进模拟退火算法的优化结果稍大，这是由于改进的模拟退火算法对于层合板铺设角度的优化问题有着较好的全局收敛性，得出的解更为精确。

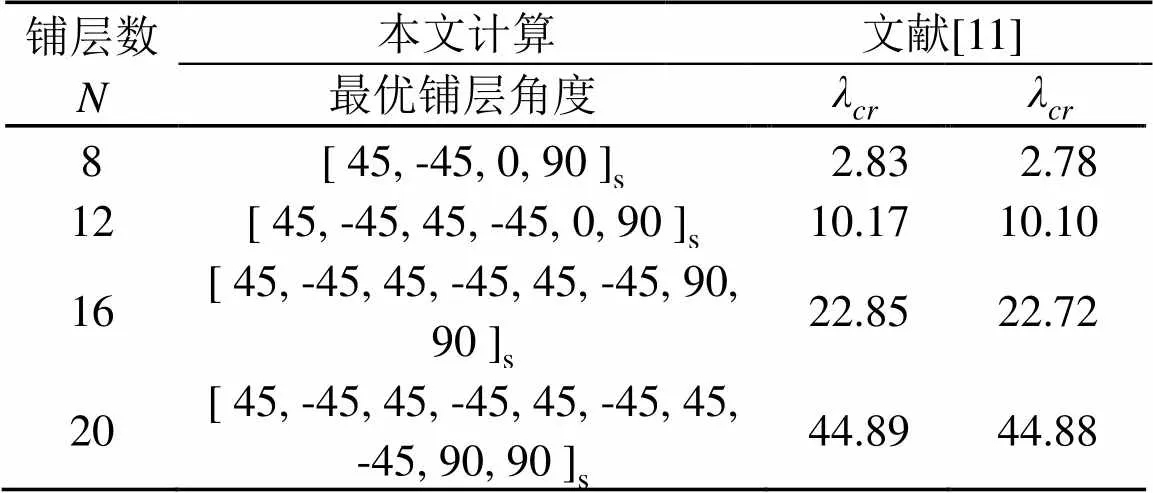
表5 长宽比等于1时层合板优化结果

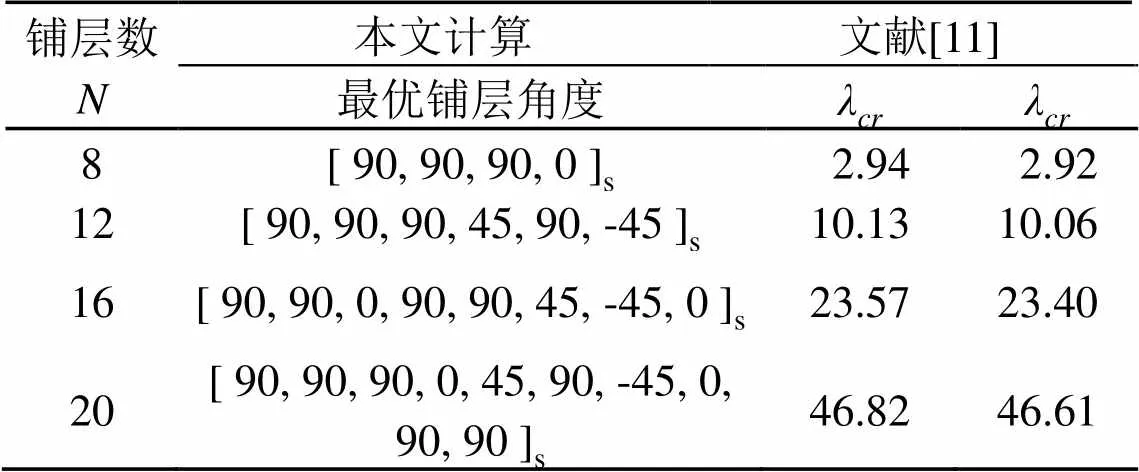
表6 长宽比a/b=1.5层合板优化结果

表7 长宽比/=2层合板优化结果

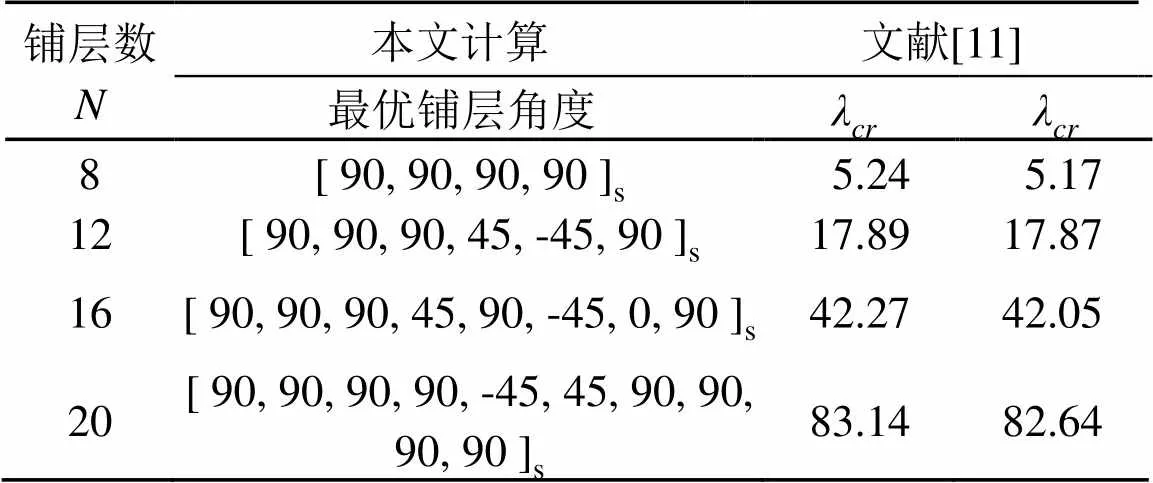
Table 5 Optimum results for a/b = 2

5 结论

(1) 通过对比改进后模拟退火算法与经典模拟退火算法的优化结果，改进后算法优化计算结果要比经典算法的结果高出17%～20%，说明改进后算法在结构优化方面有一定优势。

(2) 利用改进的模拟退火算法对复合材料层合板的屈曲进行铺层优化时，不同载荷比时算法收敛情况比较满意，当温度下降到之后时趋于收敛，并在时得到最优解；

(3) 在层合板不同铺设层数条件下，四边简支板在上下表层铺设90°或0°的铺层、同时在内部铺设较多层数的±45°铺层时，可提高层合板的临界屈曲载荷。

[1] 沈观林，胡更开. 复合材料力学[M]. 北京：清华大学出版社，2013, 10. SHEN Guanlin, HU Gengkai. Composite material mechanic[M]. Beijing: Tsinghua University Press, 2013, 10.

[2] 吴连元. 板壳稳定性理论[M]. 上海：上海交通大学出版社, 1989. WU Lianyuan. Stability theory of plates andshells[M]. Shanghai: Shanghai Jiaotong University Press, 1989.

[3] 唐文艳, 顾元宪, 赵国忠. 复合材料层合板铺层顺序优化遗传算法[J]. 大连理工大学学报, 2004, 44(2): 186-189. TANG Wenyan, GU Yuanxian, ZHAO Guozhong. Stacking-sequence optimization of composite laminated plates by genetic algorithm[J]. Journal of Dalian University of Technology, 2004, 44(2): 186-189.

[4] 穆朋刚, 赵美英, 刘关心, 等. 蚁群算法在复合材料层合板优化设计中的应用[J]. 机械强度, 2009, 31(3): 410-413. MU Penggang, ZHAO Meiying, LIU Guanxin, et al. Ant colony algorithm for composite laminate plates design and optimization [J]. Journal of Mechanical Strength, 2009, 31(3): 410-413.

[5] 修英姝, 崔德刚. 复合材料层合板稳定性的铺层优化设计[J]. 工程力学, 2005, 22(6): 212-216. XIU Yingshu, CUI Degang. Ply optimization design for stability of composite laminates[J]. Engineering Mechanics, 2005, 22(6): 212- 216.

[6] Sükrü Karakaya, Ömer Soykasap. Buckling optimization of laminated composite plates using genetic algorithm and generalized pattern search algorithm[J]. Structural and Multidisciplinary Optimization, 2009, 39(5): 477-486.

[7] 洪厚全, 李玉亮, 徐超. 复合材料层合板屈曲优化设计的模拟退火算法应用[J]. 强度与环境, 2012(6): 8-13. HONG Houquan, LI Yuliang, XU Chao. Optimization of composite laminates for buckling by simulated annealing algorithm[J]. Structure& Environment Engineering, 2012(6): 8-13.

[8] Sükrü Karakaya, Ömer Soykasap. Natural frequency and buckling optimization of laminated hybrid composite plates using genetic algorithm and simulated annealing[J]. Structural and Multidisciplinary Optimization, 2011, 43(1): 61-72.

[9] DENG Shigan, PAI Pingfeng, LAI ChihChiang, et al. A solution to the stacking sequence of a composite laminate plate with constant thickness using simulated annealing algorithms[J]. International Journal of Advanced Manufacturing Technology, 2005, 26(5/6): 499-504.

[10] Mustafa Akbulut, Fazil O. Sonmez. Design optimization of laminated composites using a new variant of simulated annealing[J]. Computers and Structures, 2011, 89(17): 1712-1724.

[11] 方秀珍. 复合材料层合板稳定性的遗传算法优化设计研究[D]. 沈阳: 东北大学, 2006.FANG Xiuzhen. Genetic algorithm optimization design of stability of composite laminates[D]. Shenyang: Northeastern University, 2006.

Influence of ply stacking sequence and ply laying angle on the stability of composite laminated plates

LI Gen, WU Jin-wu

(School of Aircraft Engineering, Nanchang Hangkong University, Nanchang 330063, Jiangxi, China)

In order to maximize the critical buckling load coefficient, the ply stacking sequence and ply laying angle of laminated composite plate are optimized with improved simulated annealing algorithm in this paper. By using parallel computation and setting up double threshold the local optimal solution appeared in the process of optimization is avoided and meantime the rate of convergence is accelerated. Fiber laying angles and stacking sequence of composite laminates plate are chosen as design variables, and the design objective function is the critical compressive load. Comparative analyses show that the optimal ply stacking sequence and ply laying angle of laminated composite plate can be obtained with improved simulated annealing algorithm.

simulated annealing algorithm; critical buckling load coefficient; ply optimization; laminated composite plates

TB332；TH113.1

A

1000-3630(2017)-04-0371-07

10.16300/j.cnki.1000-3630.2017.04.013

2016-11-18;

2017-01-29

国家自然科学基金资助项目(51265038)

李根(1989－), 男, 宁夏银川人, 博士研究生, 研究方向为结构振动控制分析。

吴锦武, E-mail: wujinwu@nchu.edu.cn