基于改进遗传算法的最小阻力功接触轮廓设计

张道德，伍 渊，胡新宇

基于改进遗传算法的最小阻力功接触轮廓设计

张道德，伍 渊，胡新宇

（湖北工业大学机械工程学院，湖北武汉430068）

对Ducker公司的公路割草机机械避障机构的接触轮廓进行优化，增长其使用寿命并使避障过程更加平稳。研究可转动构件在避障过程中所受的阻力功及与其轮廓曲线的关系。通过分析其受力状态，假设一些参数，建立该问题的数学模型，并使用遗传算法计算得到较优解。最终通过solidworks软件仿真实验验证了所设计的轮廓外形，可使机械避障接触构件在避障过程中所受的阻力功较小。

轮廓优化；避障；遗传算法；阻力功

德国Ducker公司的公路割草机采用了绕障机构来绕过路桩。其机构绕障运动过程可以简化为图1所示运动模型。

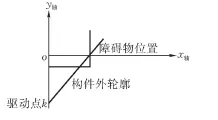
图1 绕障机构简化模型

其中，Y轴表示运动方向，构件可以绕驱动点K转动，驱动点K匀速向上移动。由于驱动点K的运动，导致构件与障碍物发生接触。构件从接触障碍到脱出障碍的过程中，始终受到障碍物对其的摩擦力和阻挡力的合力总阻力的作用。这一过程中，总阻力所做功的大小影响着驱动点运动的平稳性和构件的使用寿命，以及驱动点的能量损耗。因此设计构件的外轮廓，应使构件在从接触障碍物一直到脱离障碍物这一过程中，所受阻力功较小。

借鉴生物进化论，遗传算法将要解决的问题模拟成一个生物进化的过程，通过复制、交叉、突变等操作产生下一代的解，并逐步淘汰掉适应度函数值低的解，增加适应度函数值高的解［1］。这样进化N代后就很有可能会进化出适应度函数值很高的个体。遗传算法被广泛应用于机械优化领域。山东科技大学将适用于连续变量又有离散变量的带约束非线性目标函数的优化遗传算法用于减速器的优化［2］。王东霞等人构建了一种改进的遗传算法的机械优化设计参数模型，在传统遗传算法的基础上引入了一个修复过程，对设计中不满足约束条件的解进行修复［3］。陈新通过建立齿轮凸轮组合机构的动力学数学模型，以电机扭矩最小为优化目标，使用遗传算法对齿轮直径、减速传动比、移动凸轮总行程、冲压行程开始时间和移动凸轮型值点进行优化，最终获得有效、合理的参数［4］。因此，针对要研究的问题，可以使用遗传算法得到满足要求的优化结果。

1 模型建立

1.1 阻力公式的推导

分析上述的运动过程，发现驱动点K到构件外轮廓与障碍物接触点的距离，先减小，后增大。那么，这样必定存在一个特殊的位置，即当驱动点K运动到O点的时候，驱动点K距构件外轮廓与障碍物的接触点最近（图2）。将这一位置设为基准位置。有了基准位置，可以开始对构件做受力分析。显然，构件的受力有2种情况，即：驱动点K在基准位置下方时构件的受力和驱动点K在基准位置上方时构件的受力。

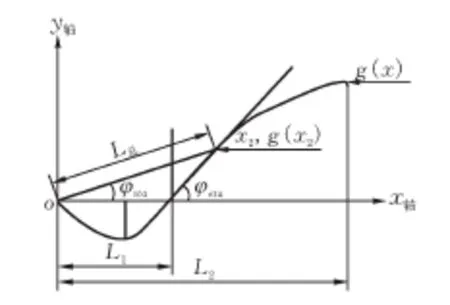
图2 构件受力分析

首先讨论驱动点K在基准位置上方时构件的受力情况。在这种情况下，构件与障碍物接触点的斜率的正负，导致摩擦力的方向不同。分以下2种情况。

1）当斜率为负时，如图3所示。

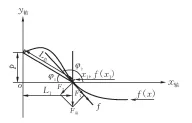
图3 驱动点在上方，轮廓斜率为负时的受力分析

此时，摩擦力f与障碍物对构件的阻力在接触点切线的分力同向

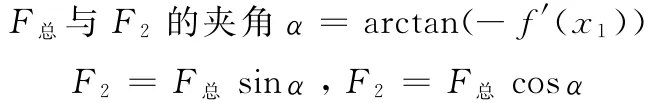
总阻力

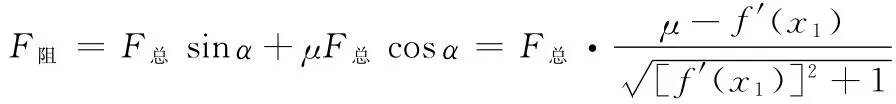
其中μ为摩擦系数。

2）当斜率为正时，如图4所示。

图4 驱动点在上方，轮廓斜率为正时的受力分析

此时，摩擦力f与障碍物对构件的阻力在接触点切线的分力反向

总阻力

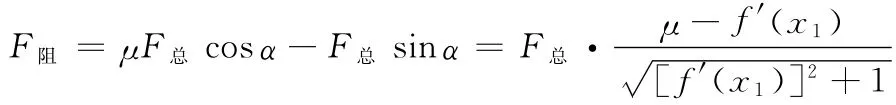
比较以上两种情况的总阻力，发现

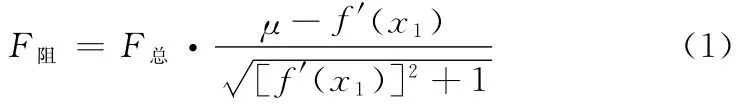
讨论驱动点K在基准位置下方时构件的受力情况。在这种情况下，构件与障碍物接触点斜率的正负，导致摩擦力的方向不同。分以下2种情况。

1）当斜率为正时，如图5所示。

图5 驱动点在下方，轮廓斜率为正时的受力分析

此时，摩擦力f与障碍物对构件的阻力在接触点切线的分力同向

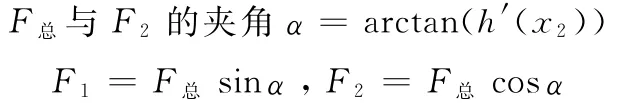
总阻力

2）当斜率为负时，如图6所示。

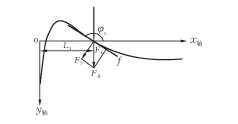
图6 驱动点在下方，轮廓斜率为负时的受力分析

此时，摩擦力f与障碍物对构件的阻力在接触点切线的分力反向

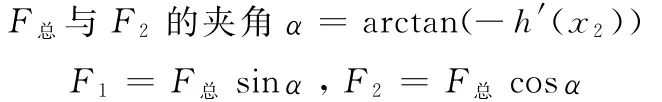
总阻力

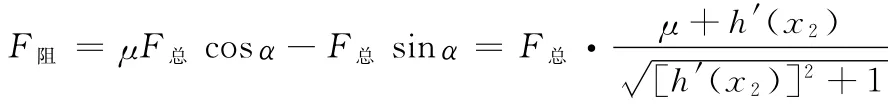
比较以上两种情况的总阻力，发现

1.2 函数方程的变换

1.2.1 驱动点K在基准位置上方时 假设图3的状态在图2的坐标系下是图2所示的状态。即设（x1，f（1））和（x2，g（x2））是同一点。由于坐标系的设定不改变角度的关系和距离大小，故在图2和图3中，L总与x1点处的切线的夹角等于L总与x2点处切线的夹角。

在图2中，L总绕（x2，g（x2））点逆时针旋转，β2＝φeta－φφsta等于在x2点处的切线与x轴正向的夹角。而

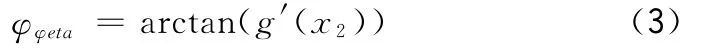
显然

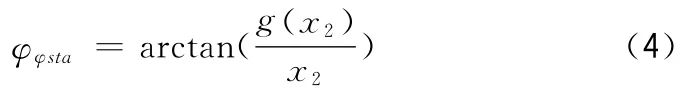
由上述分析，在图3中，L总绕（x1，f（x1））点逆时针旋转β1＝β2等于在x1点处的切线与x轴正

向的夹角

显然

带入未知量

而

其中

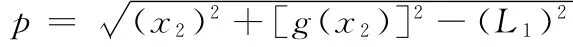
令

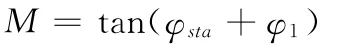
则

以上的讨论不失一般性，不论斜率的正负。

1.2.2 驱动点K在基准位置下方时 如图5所示，设此时轮廓线方程为h（x），与x轴交点为（x3，h（x3））。假设将坐标系变为图2，得到如图2所示的结果，此时（x2，g（x2））为（x3，h（x3））的映射点，即它们是同一点。用与前述相同的方法分析，发现φ2不同。

在这种情况下，

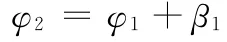
同理

令

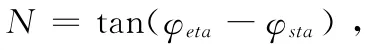
则

同样不失一般性。

1.3 建立模型

将式（7）带入式（1），将式（8）带入式（2），即可得到所用模型。

1）当驱动点K在基准位置上方时

2）当驱动点K在基准位置下方时

对上面两种情况而言，由于接触点是关于基准位置对称的，故只需对基准位置上的某点作上述两式的计算即可得到在该点为接触点时两种情况下的阻力大小。

阻力所做的功

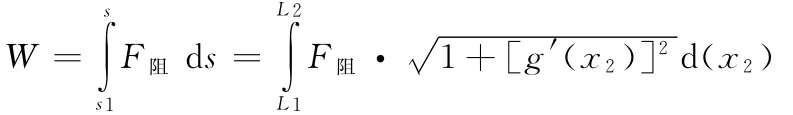
为了简化模型，不妨设障碍物对构件的反力F总是不变常量（根据需要可以合理假设F总的变化规律）。

2 编程计算

由于模型里面存在导数和积分以及求最小值的问题，且不知道g（x2）的函数表达式一般数学方法无法求解，因此使用遗传算法来搜索较优解［5］。为合理假设g（x2），不妨设其为多项式，使用多项式拟合的方法来得到合理的轮廓曲线。

但是，多项式的次数不宜取得太大以免不符合实际的轮廓尺寸。应给变量设置一定的范围来保证轮廓的尺寸。由于模型的假设，轮廓函数必须通过（0，0）和（L1，0）这两点（根据需求可以设定函数通过的点来使轮廓更加符合要求）。在基本遗传算法的基础上使用一种优化的遗传算法，即增加复制过程，将上一代中适应性最强的子代直接复制到下一代，这样就可以避免最优解被变异和交叉过程所破坏［6］。

编写遗传算法matlab程序

K＝100；%遗传代数

Np＝20；%种群大小

Nb＝［8，10］；%编码长度

L＝［－0.002，－0.05］；%值下限

u＝［0.002，0.05］；%值上限

%L＝［0，0］；%值下限

%u＝［0，0］；%值上限（两者均为零，表示轮廓为直线）tr＝0.02；%摩擦因数

Pc＝0.7；%交叉概率

Pm＝0.4；%变异概率

pop＝initpop（Np，Nb）；%初始化种群

for i＝1：K；

［objvalue］＝calobjvalue（pop，Nb，L，u，tr）；

［fitvalue，xmin，fmin］＝calfitvalue（objvalue）；

x＝decodebinary（pop，Nb，L，u）；

x（xmin，：），fmin，

［newpop1］＝selection（pop，fitvalue，xmin）；%选择

［newpop2］＝crossover（newpop1，Pc）；%交叉

［newpop3］＝mutation（newpop2，Pm）；%变异

［newpop］＝copy（newpop3，newpop1）；%复制

pop＝newpop；遗传算法程序流程图

end

以上程序是主程序，设置的模型较简单，另外，L1设置为60。x方向上的总长L2设置为80。采用3次多项式拟合，即Ax3＋Bx2＋Cx，由于通过点（60，0），可以通过方程计算出C的值。

运行程序得到最好的结果为，A＝0.0004941，B＝0.0007331，C＝－1.8227，fmin＝－142.5686。当轮廓为直线时，结果为fmin＝69.7423。由于以上设置阻力方向与摩擦力方向相同，因此fmin＜0，表明在运动过程中，总阻力做正功，帮助构件运动。最好的结果相应的轮廓外形如图7所示。

3 仿真验证

简化障碍物为球形质点，使用solidworks软件中的motion插件仿真杆件绕障的运动。分析杆件所受的摩擦力、损失功。设置摩擦系数为0.01，设置驱动点运动速度为30mm／s，根据实际的运动条件设置扭簧，使杆件能保持原有状态，弹性系数为1 Nmm／（°）。仿真场景如图8所示。

直线轮廓的仿真结果见图9—10。

优化轮廓的仿真结果见图11—12。

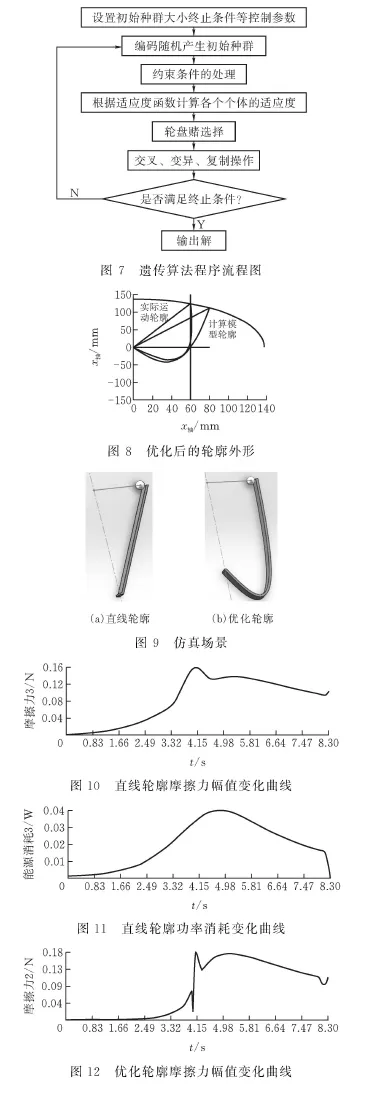
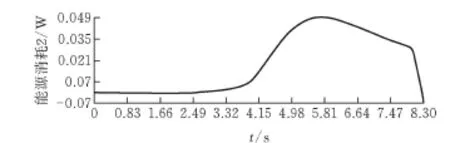
图13 优化轮廓功率消耗变化曲线

根据图7优化轮廓与x＝60的直线有两个交点，计算得出优化轮廓在仿真设置的运动速度下，前3.45s内不会接触到杆件。对比图11和图12，可以看出实验结果符合其几何条件，即直线轮廓的摩擦力最大值显然要小于优化轮廓，但优化轮廓的总消耗功小于直线轮廓，符合优化设计要求。

4 结论

通过建立物理和数学模型，假设一些状态参数，使用遗传算法能得到符合设计要求的轮廓形状，通过solidworks motion的仿真，可以看出优化后的轮廓比直线轮廓的杆件在阻力功的性能上更加优越。但由于理论和实际过程的差别，建立的模型还不够完善，还可以进一步改进。

［1］ 高峰青，王晓军.基于分支插桩的改进型评价模型及其应用［J］.计算机技术与发展，2012（10）：98－100.

［2］ 苑进，孙忠林，刘雪美.改进遗传算法在齿轮减速器优化中的应用［J］.山东科技大学学报（自然科学版），2001，20（4）：58－61.

［3］ 王东霞，张瑞玲.基于改进遗传算法的机械优化设计参数模型研究［J］.煤矿机械，2010，31（2）：9－11.

［4］ 陈新.基于遗传算法的齿轮凸轮组合机构动力学优化设计［J］.锻压装备与制造技术，2015，50（6）：38－40.

［5］ Zarei J，Poshtan J.Bearing fault detection using wavelet packet transform of induction motorφstator current［J］.Tribology International，2007，40（5）：763－769.

［6］ 曹道友.基于改进遗传算法的应用研究［D］.合肥：安徽大学，2010.

Contact Contour Design of the Minimal Resistance Based on the Improved Genetic Algorithm

ZHANG Daode，WU Yuan，HU Xinyu
（School of Mechanical Engineering，Hubei Univ.of Tech.，Wuhan 430068，China）

It is an important problem to study the mechanical obstacle avoidance mechanism of Ducker road mower，optimize the contact profile of mechanical barrier mechanism，increase its service life and make the obstacle avoiding process more stable.In this paper，the relationship between the resistance work and the contour curve of the rotatable structure in the obstacle avoidance is studied.By analyzing its stress state and assuming some parameters，the mathematical model of the problem is established，and the optimal solution is obtained by genetic algorithm.Finally，the design of the contour shape is verified by the simulation experiment of solidworks software，which can make the resistance force of the mechanical obstacle avoidance contact member in the process of obstacle avoidance.

contour optimization；obstacle avoidance；genetic algorithm；resistance

TH122

A

［责任编校：张 众］

1003－4684（2017）04－0001－05

2017－02－13

湖北省自然科学基金（2014CFA528）；湖北省自然科学基金（2016CFB653）；湖北省教育厅资助项目（D20151406）

张道德（1973－），男，湖北黄冈人，湖北工业大学教授，研究方向为机械电子工程

伍 渊（1990－），男，湖北洪湖人，湖北工业大学硕士研究生，研究方向为机械电子工程