时间模上四-点边值问题的三个正解

乔世东

(山西大同大学数学与计算机科学学院，山西大同 037009)

时间模上四-点边值问题的三个正解

乔世东

(山西大同大学数学与计算机科学学院，山西大同 037009)

多点边值问题至少有一个正解、两个正解的存在性研究较多，研究非线性边值问题至少有三个正解的存在性。

时间模；边值问题；正解；锥；不动点定理.

在最近几年，我们的前期工作[1-3]研究了一些多-点边值问题如

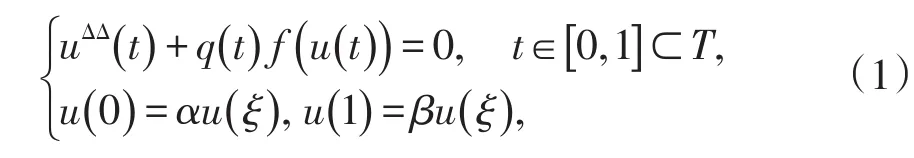
至少有三个正解的存在性。

本文研究下面的四-点边值问题

至少有三个正解的存在性。设T是一个时间模, a＜ξ＜η＜b。

引理1设条件是方程（2）的唯一解当且仅当

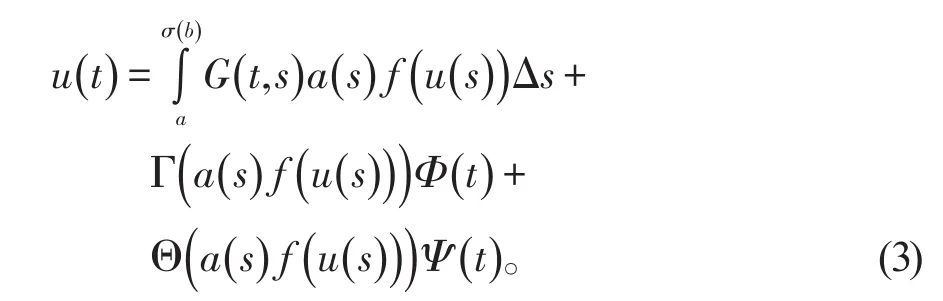
引理2设条件Λ≠0,∇≠0,则

故，引理2成立。

下面假设

引理3设条件（A1）、（A2）成立,则方程（2）的解u(t)满足

引理4设u∈P，则

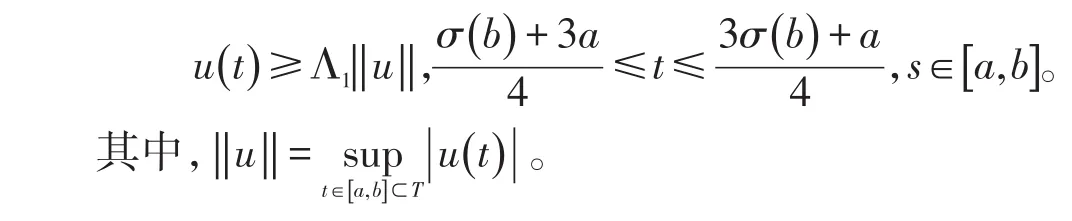
证明由引理1和引理2，

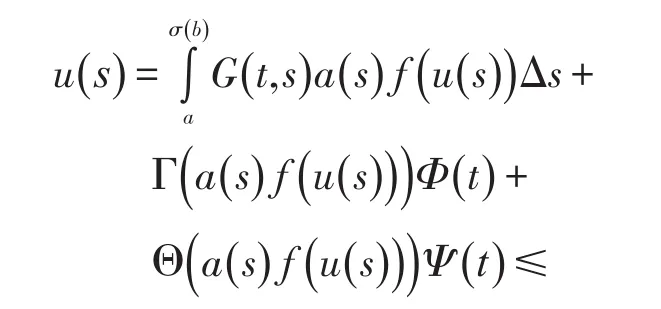
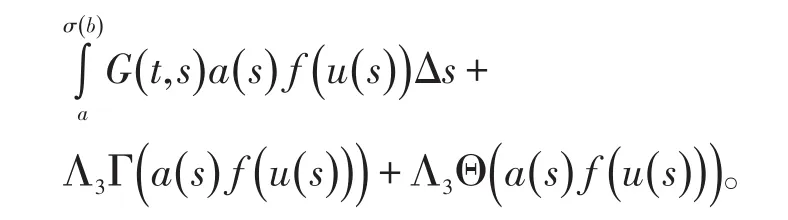
由引理2和（7）

边值问题(2)有解u=u(t)，当且仅当u是下列算子方程的解。

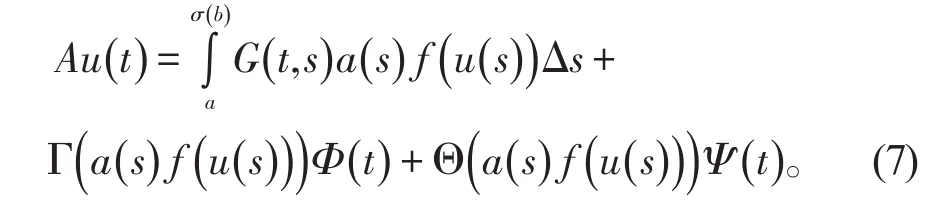
定理1[4](Legget-Williams)设P是实巴拿赫空间E的一个锥,

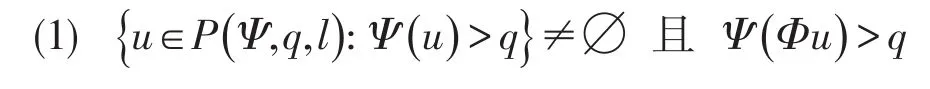
（2）当‖u‖≤p时，有‖Φu‖≤p；

定理2设条件(A1)～(A2)成立,又设存在常数0＜p＜q≤r满足:

则边值问题 (2)至少有三个正解 u1,u2,u3,满足u1(ξ)＜p,u2(η )＞q,p＜u3(ξ)当u3(η )＜q。

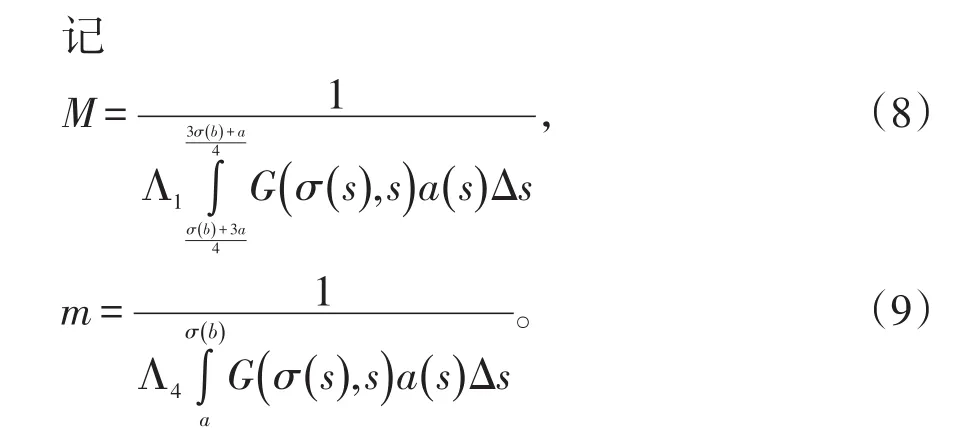
证明定义非负连续的凸函数满足其中P,λ,μ如同(6),(8),(9),对所有的。设,则‖u‖≤r,由假设条件(B1)知

所以，有

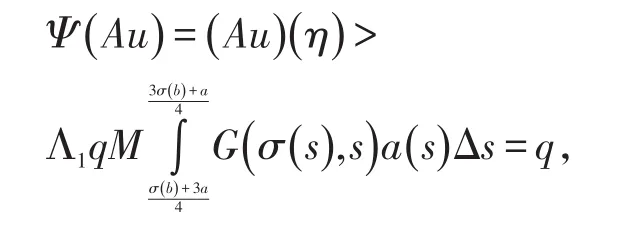
定理1的条件（1）满足。

如果‖u‖≤p,则f(u)＜pm,由条件(B3),

定理1的条件（2）满足。

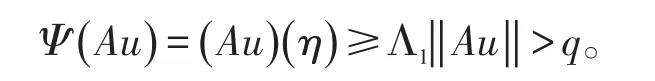
定理1的条件（3）满足。

所以边值问题(2)至少有三个正解u1,u2,u3,满足

[1]张英.时间模上二阶4-点边值问题的三个正解的存在性[J].山西大同大学学报(自然科学版)，2016，32（2）：1-3.

[2]张英，乔世东.时间模上一阶非线性边值问题的三个正解[J].山西大同大学学报(自然科学版)，2010,26（5）：1-3.

[3]张英.时间模上二阶3-点边值问题的三个正解[J].北京工商大学学报，2009（5）：15-18.

[4]LEGGET R W,WILLIAMS L R.Multiple Positive Fixed Points of Nonlinear Operators on Ordered Banach Spaces[J].Indiana Univ. Math.,1979（28）:673-688.

Existence of Three Positive Solutions to a Four-point Boundary Value Problems on Time Scales

QIAO Shi-dong
(School of Mathematics and Computer Sciences,Shanxi Datong University,Datong Shanxi，037009)

Some results are obtained for the existence of at least one,two positive solutions of mul-point boundary value problem. In this paper,we study the existence of at least three positive solutions.

time scales;boundary value problem;positive solution;cone;fixed point theorem

175.14

A

〔责任编辑 高海〕

1674-0874(2017)04-0001-03

2017-03-16

乔世东（1963-），男，山西左云人，硕士，教授,研究方向:代数与方程。