聚焦运算本质 关注融会贯通

◎栾晓婕

聚焦运算本质 关注融会贯通

◎栾晓婕

《义务教育数学课程标准（2011年版）》中指出：运算能力主要是指能够根据法则和运算律正确地进行运算的能力。培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。由此可见，运算能力已经改变了追求“又快又对”的传统要求，而重视的是让学生经历探索、发现计算方法的过程。

一、借助学生已有经验，独立解决问题

课始，出示问题情境，要求学生列出算式。

师：为什么用除法来解决？

师：对，求一个数里有几个另一个数，用除法计算，这个除数可以是整数，也可以是分数。看来，分数除法和整数除法的意义是相通的。

这一环节是让学生体会一个数除以分数的意义，因为运算意义是建立计算法则的基础，又是应用这种运算的依据。基于以上认识，对除法意义的理解应该成为分数除法教学的首要环节。

（学生自己尝试解决，小组讨论后全班交流，同时教师巡视，搜集学生作品。）

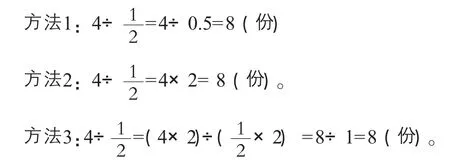
师：这三种做法你看懂了吗？能讲出每种做法的道理吗？

生1：第一种做法是把分数转化为小数来计算。

生3：第三种做法是根据商不变的性质，将被除数和除数同时×2，这样除数就变成了整数，所以4÷

师：（追问） 为什么同时×2？×3可以吗？×4呢？哪个更简单？

生4：同时×2，这时除数就变成整数1，×3后除数还是分数，没有转化为整数，×4也可以，这样4÷但没有×2更简单。

生5：同时×2简单，这个2也就是除数 的倒数，这时除数就变成整数1，任何数除以1都等于原数。

师：的确是这样，除数变为1，更方便我们计算。同学们，刚才我们遇到一个新问题，我们能积极开动脑筋，把一个新问题转化成学过的知识来解决，看来转化是解决问题的好方法。还愿意分饼吗？我们再看一个问题。

（出示第二个问题：4张同样大的饼○○○○，每张一份，○○○○可以分成几份？）

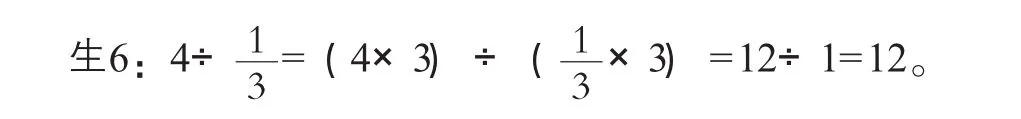
生7：我发现这道题不能转化为小数除法计算，因此将被除数和除数同时乘除数的倒数，这时除数就变为1，好算。

师：对，同时乘除数的倒数，题目就变得如此简单，这就是倒数的魅力。这个结果到底对不对呢，你

能用其他方法验证一下吗？

师：验证之后，更加确信除数是分数的除法可以根据商不变的规律，同时乘除数的倒数的方法来解决。

借助学生已有经验，独立解决问题，在多样化的算法之中，呈现了学生不同的认知水平，既有直观运算的通俗易懂，又有抽象运算的合情合理。在读懂不同水平的算法之后，对利用商不变的性质这种做法进行追问，学生初步理解了这种做法的算理，并通过第二次分饼的练习体会利用这种方法解决问题的优化。由于数据简单，便于口算，整个推算过程处在学生思维能力的最近发展区内，因此降低了学生探究算法、理解算理的难度。

二、对比发现，总结运算法则

师：刚才我们练习的除法问题除数都是几分之一，如果除数是几分之几，这种方法还好用吗？现在我们继续挑战解决分饼问题。

（出示题目：4张同样大的饼○○○○，每张一份，○○○○可以分成几份？ 要求学生独立用商不变的规律解决，并验证这种做法的合理性，看看又有什么新的发现。）

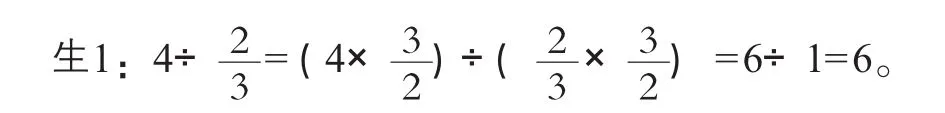
生3：我发现利用商不变规律对除数是几分之几的除法同样适用，但要注意被除数、除数同时乘除数的倒数，这样除数变为1，非常好算。

生4：我发现除数是分数的除法的计算，只要把被除数、除数同时乘除数的倒数，转化为除数是1的除法，就可以迎刃而解。

师：刚才我们用商不变的性质解决了3个问题，并用分一分的方法加以验证，对比看看我们整理的计算过程，你有什么发现？

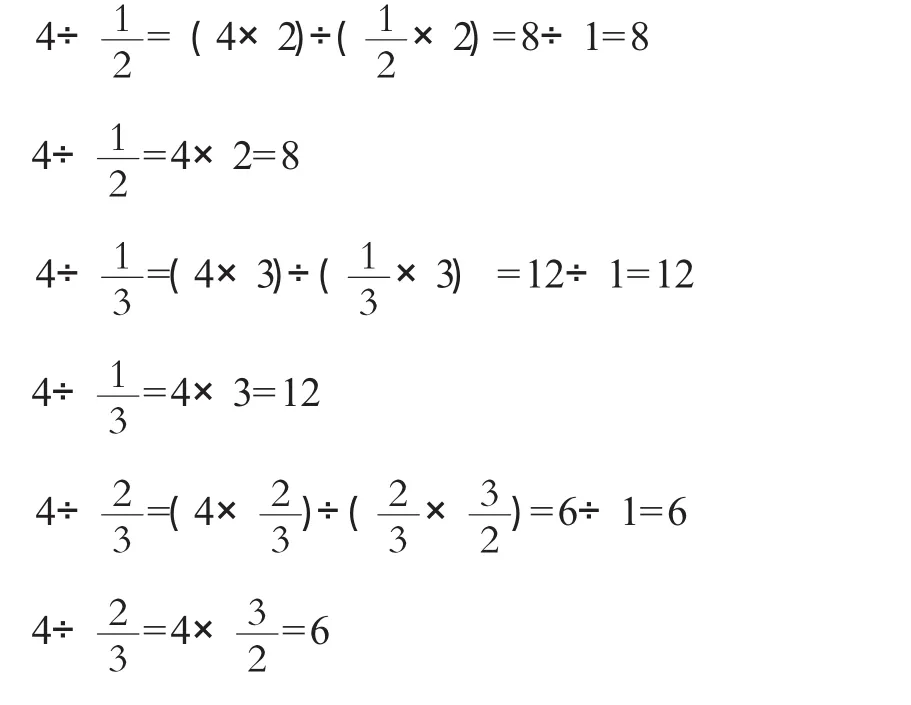
生5：左边的都是用商不变的规律，把除数转化为1来计算；右边的除法都变成乘除数的倒数。

生6：右边的算法是左边的简便写法，因为把除数转化为1，任何数除以1，都等于它本身，除数1可省略，就和右面算式一样了。

生7：既然是简便写法，那计算分数除法不用同时乘倒数，只把被除数乘除数的倒数就可以了，可以省略一步。

生8：在学习小数除法时，我们是利用商不变规律把小数除法转化为整数除法；现在，我们又可以利用这个规律解决分数除法问题。

生9：对，除以一个不为零的数，等于乘这个数的倒数。这个数可以是整数，也可以是分数。

师：通过三次分饼的过程，我们利用商不变规律逐渐探索出除数是分数的除法的计算方法，这种规律不仅适用于小数除法，同样也适用于分数除法；并能优化这种方法，使计算变得更加简洁。其实，只要我们用心观察思考，很多知识都是相通的。

数学是严谨的科学，如果仅仅从直观模型中总结出方法，势必认识不深刻。上面的设计从学生已有知识出发，通过发现、验证等活动，学生逐渐认识到“除以一个数，等于乘这个数的倒数”的方法是应用商不变规律的简化形式，并把分数除法的计算方法与以前学过的小数除法知识纳入一个知识框架中，学生能融会贯通，深刻理解算理的本质。

（作者单位：瓦房店市教师进修学校）

（责任编辑：杨强）