浅谈在VB教学中引导学生建立数学模型
沈建武
【摘要】本文主要讲解利用VB编程解决数学课程里的利润最大值问题,引导学生加强题意分析,结合数学知识,建立数学模型,然后根据数学模型设计算法并利用程序设计语言编程解决实际问题。
【关键词】VB 数学模型 If语句 For循环
【中图分类号】G632.4 【文献标识码】A 【文章编号】2095-3089(2017)30-0075-02
在数学课程里,学生常常会遇到较为复杂繁琐的实际问题,学生一时难以求解,而运用计算机编程解决往往会变得有效、便捷多。在编程解决具体问题中应引导学生把实际问题抽象为数学模型,我们除已知的数学概念、数学公式可直接利用外,还可根据题意建立方程组、不等式组、函数式、运算式、递推式等等。
一、结合具体问题,理清解题思路
问题:某太阳能设备厂在计划期内拟生产甲、乙、丙三种适销产品,每件销售利润分别为4万元、3万元、2万元。按工艺规定,甲、乙、丙三种产品都需要在A、B、C、D四种不同的设备上加工,其中甲产品生产需在A、B、C、D四种设备上加工的台时数分别为2、1、4、0;乙产品为2、2、0、4;丙产品为1、1、0、0。已知A、B、C、D四种设备在计划期内有效使用台时数分别为12、8、16、12。如何安排生产可使利润最大?
通过问题描述不难看出这是个典型的线性规划问题,我们主要通过构造相应的目标函数来求得生产利润最大值。
1. 分析问题
设甲、乙、丙三种产品的产量分别为x、y、z件,利润总额为f(x, y, z),根据题意,构造x、y、z变量的约束条件应满足如下不等式组:
构造以x、y、z为变量的目标函数f(x, y, z)=4x+3y+2z,计算f(x, y, z)值的可行域。
2. 加强题意分析,寻找解题思路和方法
根据不等式组可知,x、y、z是自然数且满足:0≤x≤4,0≤y≤3,0≤z≤8。这样,可采用穷举的方法,在许可的范围内寻找适当的x、y、z,求出利润总额f(x, y, z)一系列的值,这一系列值的集合即为f(x, y, z)的可行域。在可行域的一系列f(x, y, z)值中找出最大f_max值,即为所求的生产利润最大。
以上所述为解决线性规划问题的一般思路,学生容易理解,但实际求解时需做大量的判断和计算,人工计算非常繁琐,一时半刻求不出正确的答案;若编写程序让计算机完成,则可充分发挥计算机运算速度快、计算准确的特点。
二、VB语言实现数学中的关键问题
1. 约束条件的实现
VB中的If语句很方便的实现约束条件的判断,其中多个不等式应同时成立正好可用VB中的逻辑运算符And(与运算:当两个操作数同时为真时,结果才为真)相连接。
2. VB中For循环可表示x、y、z的变化
根据题意和分析不等式组可知,x可从0变化到4,y可从0变化到3,z可从0变化到8,在程序设计中应对x、y、z值作离散化处理,本题中,x,y,z∈N(N表示自然数),故可将x、y、z的变化量设为1,利用VB提供的For语句三重循环可以方便地表示x、y、z变化。
3. 目标函数f(x, y, z)最大值的求解
利润总额f(x, y, z)是一系列值的集合,用VB编程求其中的最大值f_max。
①把满足不等式组的x、y、z代入f(x, y, z)=4x+3y+2z中求出一系列值存放在定义的数组f中。
②开始假设利润总额最大值f_max=0
③利用VB的三重for循环依次取出存放在数组f中的数并与f_max比较大小,若f_max< f(x, y, z),则f_max= f(x, y, z),直至循环结束,最后f_max中存放的就是f(x, y, z)中的最大值,从而得出利润总额的最大值。
三、VB程序设计
本程序的界面非常简单,只需一个窗体(Form1)、一个命令按钮(Command1)即可,命令按钮的单击事件过程代码如下(单引号后面为程序代码注释):
Private Sub Command1_Click()
Dim x, y, z As Integer
Dim x_max, y_max, z_max, f_max As Integer
Dim f(4, 3, 8) As Integer '定义存放函数f (x,y,z)值的数组f
'把满足不等式组的x、y、z代入 f (x,y,z)=4x+3y+2z中求值存入数组
For x = 0 To 4
For y = 0 To 3
For z = 0 To 8
If (2 * x + 2 * y + z <= 12) And (x + 2 * y + z <= 8) Then
f(x, y, z) = 4 * x + 3 * y + 2 * z
Else
f(x, y, z) = 0
End If
Next z
Next y
Next x
f_max = 0 '初始化最大值变量f_max为0
'依次取出数组f (x,y,z) 中所有的值,找出最大值存放在变量f_max
For x = 0 To 4
For y = 0 To 3
For z = 0 To 8
If f_max < f(x, y, z) Then
f_max = f(x, y, z)
x_max = x
y_max = y
z_max = z
End If
Next z
Next y
Next x
Print "当x="; x_max; ",y="; y_max; ",z="; z_max; "时,"
Print " f (x,y,z)的最大值="; f_max
End Sub
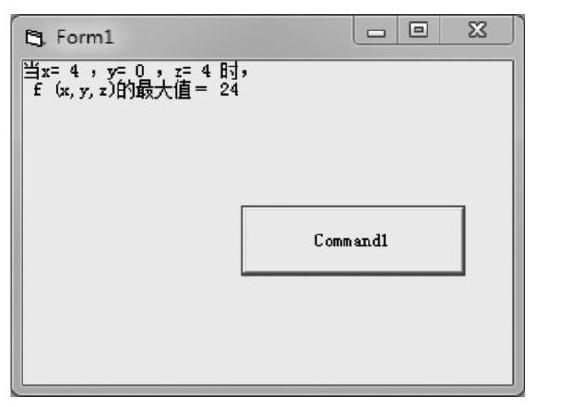
运行程序,单击命令按钮(Command1),立即在窗体上显示结果如图所示。
若想探究目标函数f(x, y, z)中具体有哪些值,可在程序代码“f(x, y, z) = 4 * x + 3 * y + 2 * z”后面回车换行输入“Print f(x, y, z)”,运行程序,单击命令按钮(Command1),窗体上会分行显示下列数值:0、2、4、6、8、10、12、14、16、3、5、7、9、11、13、15、6、8、10、12、14、9、11、13、4、6、8、10、12、14、16、18、7、9、11、13、15、17、10、12、14、16、13、15、8、10、12、14、16、18、20、11、13、15、17、19、14、16、18、17、12、14、16、18、20、22、15、17、19、21、18、20、16、18、20、22、24、19、21、23、22,最后再顯示上图所示最大值信息。
通过本文的叙述不难看出,编写程序求解数学中相对复杂的线性规划问题很方便、快捷,而且程序设计的通用性强,对于不同的线性规划问题,只需要改变x、y、z的变化范围、约束条件和目标函数即可,所以计算机程序设计实现数值计算也成为数学建模的常用方法,这不仅能快速、准确的得到计算结果,同时也为问题的求解提供了新的思路。
参考资料:
[1]信息技术(选修1)算法与程序设计,广东教育出版社.
[2]普通高中数学新课程标准(实验),中华人民共和国教育部.
[3]杨振山等.大学计算机基础简明教程[M].北京:高等教育出版社.
[4]李佐锋.数学建模[M].中国广播电视大学出版社 .
课程教育研究·上2017年30期
