G-内射模的直和与G-平坦模的直积问题
陈 东, 王芳贵, 胡 葵
( 1. 成都大学 信息科学与工程学院, 四川 成都 610106; 2. 四川师范大学 数学与软件科学学院, 四川 成都 610066; 3. 西南科技大学 理学院, 四川 绵阳 621010)
G-内射模的直和与G-平坦模的直积问题
陈 东1, 王芳贵2*, 胡 葵3
( 1. 成都大学 信息科学与工程学院, 四川 成都 610106; 2. 四川师范大学 数学与软件科学学院, 四川 成都 610066; 3. 西南科技大学 理学院, 四川 绵阳 621010)
证明在Artin环上,G-内射模的直和是G-内射模,G-平坦模的直积是G-平坦模.进一步证明在Noether环R上,若每个R-模的G-内射维数有限,则G-内射模关于直和封闭;在凝聚环R上,若每个R-模的G-平坦维数有限,则G-平坦模关于直积封闭.
G-内射模; G-平坦模; Noether环; 直和; 直积
1 预备知识
1969年,M. Auslander等[1]首先对Noether环上的有限生成模引入了G-维数为零的模.1995年,E. E. Enochs等[2]把这一概念推广到任意环和非有限生成模上,于是得到所谓的Gorenstein投射模的概念,同时也引入了Gorenstein内射模的概念.设M是R-模,若存在内射R-模的正合列
E:=…→E1→E0→E0→E1→…,
(1)

F:=…→F1→F0→F0→F1→…,
(2)
使得M≌(F0→F0),且对任意内射R-模I,该正合列在函子I⊗-的作用下仍是正合的.正合列(2)也叫做M的全平坦分解.2007年,D.Bennis等[4]又引入了强G-投射模、强G-内射模和强G-平坦模.模M称为强G-内射模,是指存在正合列0→M→E→M→0,其中E是内射模,使得对任何内射模I,诱导序列0→HomR(I,M)→HomR(I,E)→HomR(I,M)→0仍是正合列;模M称为强G-平坦模,是指存在正合列0→M→F→M→0,其中F是平坦模,使得对任何内射模I,诱导序列0→I⊗RM→I⊗RF→I⊗RM→0仍是正合列.内射模(或平坦模)是强G-内射模(或强G-平坦模),强G-内射模(或强G-平坦模)是G-内射模(或G-平坦模).像经典的同调理论那样,文献[5-7]先后引入了模M的G-投射维数(G-pdRM)、G-内射维数(G-idRM)和G-平坦维数(G-fdRM),这里不作赘述.
由Cartan-Eilenberg定理,环R是Noether环当且仅当内射R-模的直和是内射模;由Chase定理,环R是凝聚环当且仅当平坦R-模的直积是平坦模.人们自然要问,G-内射模的直和是G-内射模是否还是Noether环的刻画?相应地,G-平坦模的直积是G-平坦模是否还是凝聚环的刻画?
2011年,L.W.Christensen等[8]证明了G-内射模的直和是G-内射模的环是Noether环;然而对其逆命题(即Noether环上G-内射模的直和,以及凝聚环上G-平坦模的直积问题)直接地证明就显得十分困难.2006年,L.W.Christensen等[9]证明了若R是具有有限krull维数的Gorenstein环的同态像,则R上的每个G-内射模的直和是G-内射模,每个G-平坦模的直积也是G-平坦模.2009年,LiuZ.K. 等[10]证明了左Artin环上,若每个单模的内射包有限生成,则每个G-平坦模的直积也是G-平坦模.2011年,D.Murfet等[11]证明了在Noether环R上,若对每个非极大的素理想p,Rp是Gorenstein环,则G-平坦模的直积也是G-平坦模.本文证明了在交换Artin环上,G-内射模的直和是G-内射模,进一步证明了G-平坦模的直积也是G-平坦模;还证明了在Noether环R上,若每个R-模的G-内射维数有限,则G-内射模的直和是G-内射模;在凝聚环R上,若每个R-模的G-平坦维数有限,则G-平坦模的直积也是G-平坦模.
本文恒设R是交换环,模均指R-模,E(M)表示模M的内射包.gl.dim(R)表示R的整体维数,w.gl.dim(R)表示R的弱整体维数,idRM与fdRM分别表示R-模M的内射维数与平坦维数.
2 主要结果
首先讨论在一类特殊的Noether环(Artin环)上,G-内射模的直和与G-平坦模的直积问题.为讨论方便,需要有如下2个引理:
引理 1[12]设R是Noether环,E是非零的内射模;则E可以分解为不可分解内射模的直和,且每一不可分解的内射模可以表示为E(R/p),其中p是R的素理想.
引理 2[13]设R是Noether局部环;则R有非零的有限生成内射模当且仅当R是Artin环,当且仅当dim(R)=0.
命题 3 设R是Artin环,E是非零的内射模;则E可以分解为有限生成内射模的直和.
证明 由文献[14],Artin环可以分解为有限个Artin局部环的直积.记R=R1×R2…×Rs,其中R1,R2,…,Rs都是Artin局部环.于是有E=E1×E2×…×Es,其中Ei是内射Ri-模.故不妨设R是Artin局部环,其唯一素理想为m.由引理1,E是一些E(R/m)的直和.由引理2,R有有限生成的内射模E0.自然地,E0是有限个E(R/m)的直和,故E(R/m)一定是有限生成的,于是得到E是有限生成内射模的直和.
以下定理讨论Artin环上G-内射模的直和问题.
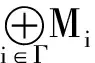

E:=…→E1→E0→E0→E1→…,

⊕E:=…→⊕E1→⊕E0→⊕E0→⊕E1→….


由于Mi是G-内射模,故对任何下标i和j,有
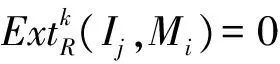
于是得到


将看到,Artin环上G-平坦模的直积仍然是G-平坦模.


F:=…→F1→F0→F0→F1→…,
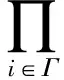
∏F:=…→∏F1→
∏F0→∏F0→∏F1→…,

由于Mi是G-平坦模,故对任何下标i和j,有

于是得到


对于Noether环上G-内射模的直和问题,以及凝聚环上G-平坦模的直积问题,讨论起来很困难,至今未完全解决.2011年,文献[8]把它作为公开问题.近年来,许多学者对该问题给了部分证明,参见文献[9,11].下面讨论Noether环上G-内射模的直和及凝聚环上G-平坦模的直积是否封闭,为讨论方便,需引入一些概念.2013年,GaoZ.H.[15]引入了泛G-内射模的概念.模M称为泛G-内射模,是指M有全内射分解
E:=…→E1→E0→E0→E1→…,
(3)
使得M≌ker(E0→E0).相应地,文献[15]还引入了泛G-平坦模的概念.模M称为泛G-平坦模,是指M有全平坦分解
F:=…→F1→F0→F0→F1→…,
(4)
使得M≌ker(F0→F0).自然地,G-内射模是泛G-内射模,G-平坦模是泛G-平坦模.
定义 6 设M是R-模.
1) 若有正合列0→M→E→M→0,其中E是内射模,则M称为强泛G-内射模.
2) 若有正合列0→M→F→M→0,其中F是平坦模,则M称为强泛G-平坦模.
显然,强G-内射模是强泛G-内射模,强泛G-内射模是泛G-内射模;强G-平坦模是强泛G-平坦模,强泛G-平坦模是泛G-平坦模.容易看到,M是强G-内射模当且仅当M既是G-内射模,又是强泛G-内射模;M是强G-平坦模当且仅当M既是G-平坦模,又是强泛G-平坦模.以下定理,讨论强泛G-内射模的直和与强泛G-平坦模的直积问题.
定理 7 若R是Noether环,则强泛G-内射模的直和是强泛G-内射模;若R是凝聚环,则强泛G-平坦模的直积是强泛G-平坦模.
证明 设M是强泛G-内射模,故存在以下内射模的正合列

使得M≌ker(f).由R是Noether环,从而⊕E也是内射模,故又有正合列

使得⊕M≌ker(f′),其中Mi=M.因此,强泛G-内射模的直和是强泛G-内射模.同理,也可以证明在凝聚环上,强泛G-平坦模的直积是强泛G-平坦模.
引理 8 1) 若每个R-模有有限的G-内射维数,则强泛G-内射模是强G-内射模.
2) 若每个R-模有有限的G-平坦维数,则强泛G-平坦模是强G-平坦模.
证明 1) 设M是强泛G-内射模,故有正合列0→M→E→M→0,其中E是内射模.设G-idRM=n,拼接该正合列n次,得到正合列
0→M→E1→E2→…→En-1→En→M→0,
其中每个Ei=E.于是有M是G-内射模.故得到M是强G-内射模.
2) 设M是强泛G-平坦模,故有正合列0→M→F→M→0,其中F是平坦模.设G-fdRM=n,拼接该正合列n次,得到正合列
0→M→F1→F2→…→Fn-1→Fn→M→0,
其中每个Fi=F.于是有M是G-平坦模.故得到M是强G-平坦模.
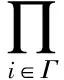
证明 由文献[4]的定理3.5,G-平坦模是强G-平坦模的直和加项,故可设Qi=Mi⊕Ni,其中Qi是强G-平坦模.于是

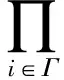
设0→Mi→Fi→Mi→0是正合列,其中Fi是平坦模.于是有正合列

用类似的方法可以证明:
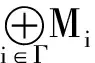
证明 由文献[4]的定理2.7,G-内射模是强G-内射模的直和加项,故可设Qi=Mi⊕Ni,其中Qi是强G-内射模.于是


设0→Mi→Ei→Mi→0是正合列,其中Ei是内射模.于是有正合列

近年来,Gorenstein环在研究Gorenstein理论中受到广泛的关注.一个环R称为Gorenstein环,是指R是Noether环,且R的自内射维数有限(idRR<∞).环R称为n-Gorenstein环,是指R是Noether环,且R的自内射维数不超过n,其中n≥0.特别地,QF环就是0-Gorenstein环.
推论 11 设R是n-Gorenstein环,则每个G-内射模的直和是G-内射模.
证明 由文献[16]的定理12.3.1,n-Gorenstein环上每个R-模M的G-内射维数有限(G-idRM≤n),再由定理10,G-内射模的直和是G-内射模.
1996年,Din N. Q.等[17]引入了n-FC环的概念.一个环R称为n-FC环,是指R是凝聚环,且R的自FP内射维数小于等于n(FP-idRR≤n).特别地,0-FC环称为FC环,FC环也是IF环.文献[17]同时证明了环R是FC环当且仅当每个R-模是G-平坦模.2013年,Gao Z. H.[15]证明了环R是FC环当且仅当每个R-模是泛G-平坦模.
推论 12 设R是n-FC环,则每个G-平坦模的直积是G-平坦模.
证明 由文献[17]的定理7,n-FC环上每个R-模M的G-平坦维数有限(G-fdRM≤n),再由定理9,G-平坦模的直积是G-平坦模.
由G-内射模的定义知,每个内射模都是G-内射模,反之,G-内射模不一定是内射模.由文献[5]知,对任意的G-内射模M,M是内射模当且仅当idRM<∞.下面给出G-内射模是内射模的一个充分条件.同时可以看到,在这个条件下,每个G-平坦模也是平坦模.
定理 13 1) 设M是G-内射模,若对R的任意非零理想I,有idRR/I<∞,则M是内射模.
2) 设M是G-平坦模,若对R的任意非零理想I,有idRR/I<∞,则M是平坦模.


容易看到,在定理13条件下,有Noether环上每个G-内射模的直和是G-内射模,凝聚环上每个G-平坦模的直积是G-平坦模.
[1] AUSLANDER M, BRIDGER M. Stable Module Theory[M]. Providence RI:Am Math Soc,1969,94(94):1-146.
[2] ENOCHS E E, JENDA O M G. Gorenstein injective and projective modules[J]. Math Z,1995,220(1):611-633.
[3] ENOCHS E E, JENDA O M G, TORRECILLAS B. Gorenstein flat modules[J]. 南京大学学报数学(半年刊),1993,10(1):1-9.
[4] BENNIS D, MAHDOU N. Strongly Gorenstein projective, injective and flat modules[J]. J Pure Appl Algebra,2007,210(2):437-445.
[5] HOLM H. Gorenstein homological dimensions[J]. J Pure Appl Algebra,2004,189(1):167-193.
[6] HOLM H. Rings with finite Gorenstein injective dimension[J]. Proc Am Math,2004,132(5):1279-1283.
[7] BENNIS D, MAHDOU N. Global Gorenstein dimensions[J]. Proc Am Math,2010,138(2):461-465.
[8] CHRISTENSEN L W, FOXBY H B, HOLM H. Beyond totally reflexive modules and back[C]. FONTANA M, KABBAJ S E, OLBERDING B, et al. Commutative Algebra. New York:Springer-Velarg,2011:101-143.
[9] CHRISTENSEN L W, FOXBY H B, HOLM H. On Gorenstein projective, injective and flat dimensions:a functorial description with applications[J]. J Algebra,2004,302(1):231-279.
[10] LIU Z K, YANG X Y. Gorenstein projective, injective and flat modules[J]. J Aust Math,2009,87(3):395-407.
[11] MURFET D, SALARIAN S. Totally acyclic complexes over Noetherian schemes[J]. Adv Math,2011,226(2):1096-1133.
[12] MATLIS E. Injective modules over Noetherian rings[J]. Pac J Math,1958,8(3):512-528.
[13] FAITH C, WALKER E A. Direct-sum representations of injective modules[J]. J Algebra,1967,5(2):203-221.
[14] 王芳贵. 交换环与星型算子理论[M]. 北京:科学出版社,2006.
[15] GAO Z H. Weak Gorenstein projective,injective and flat modules[J]. J Algebra Appl,2013,12(2):961-973.
[16] ENOCHS E E, JENDA O M G. Relative Homological Algebra[M]. Berlin:Walter De Gruyter,2000.
[17] DING N Q, CHEN J L. Coherent rings with finite self-FP-injective dimension[J]. Commun Algebra,1996,24(9):2963-2980.
2010 MSC:13E10
(编辑 余 毅)
The Problems on the Direct Sum of G-injective Modules and the Direct Product of G-flat Modules
CHEN Dong1, WANG Fanggui2, HU Kui3
(1.CollegeofInformationScienceandEngineering,ChengduUniversity,Chengdu610106,Sichuan; 2.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan; 3.CollegeofScience,SouthwestUniversityofScienceandTechnology,Mianyang621010,Sichuan)
It is proved that, over Artinian rings, the direct sum of Gorenstein injective modules is still Gorenstein injective and the direct product of Gorenstein flat modules is still Gorenstein flat. Moreover, it is proved that, if R is a noetherian ring on which every R-module has finite Gorenstein injective dimension, the class of Gorenstein injective modules is closed under arbitrary direct sums, and if R is a coherent ring on which every R-module has finite Gorenstein flat dimension, the class of Gorenstein flat modules is closed under arbitrary direct products.
G-injective module; G-flat module; Noetherian ring; direct sum; direct product
2016-12-21
国家自然科学基金(11671283)和教育部博士点专项科研基金(20125134110002)
O154
A
1001-8395(2017)04-0486-05
10.3969/j.issn.1001-8395.2017.04.010
*通信作者简介:王芳贵(1955—),男,教授,主要从事交换代数、同调代数与代数K-理论的研究,E-mail:wangfg2004@163.com

