一类二阶抛物型方程初边值问题解的存在定理
冯艳青,王忠英,姚俊,文传军
(常州工学院数理与化工学院,江苏常州213000)
一类二阶抛物型方程初边值问题解的存在定理
冯艳青,王忠英,姚俊,文传军
(常州工学院数理与化工学院,江苏常州213000)
本文研究了一类二阶非线性抛物型方程解的存在唯一性问题.利用非线性分析中的吸引盆理论和同胚理论,获得了相应的二阶非线性抛物型方程初边值问题解的大范围存在唯一性定理.
二阶抛物型方程;初边值问题;吸引盆;全局同胚
1 引言
二阶抛物型方程

也被称为热传导方程,其中Δ表示n维拉普拉斯算子.由于在物理、几何中的广泛应用,许多数学工作者都研究过方程(1)解的存在性问题,也得到很多结果(见文献[1-5]).
在抛物型偏微分方程解的存在性问题的研究中,一般是先建立一个可能的解的先验估计,然后利用一些非线性分析的方法证明解的存在性.如Elcart和Sigillito在文[1]中先推导出了抛物算子Lau
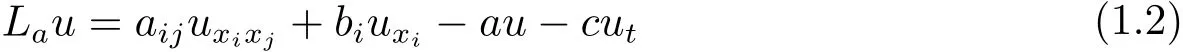
的一个先验估计kuk2,1≤CkLuk0,进而得到了解存在唯一性定理.受到上述思想的启发,我们将对二阶抛物型算子

建立一个优先估计

然后利用非线性分析的方法讨论方程(1.1)解的存在性问题,并推导出一类二阶抛物型方程初边值问题解的存在唯一性的一个充分条件.我们的证明不同于Elcart和sigillito给出的证明.一个有趣的工具,吸引盆,在我们的主要定理2.1的证明中起着重要的作用,下面先给出有关吸引盆理论的相关知识.
引理1.1[6]设E,F为Banach空间,H为E中连通开集.f:H⊂E→F在H上是局部同胚的C1映射.设x0∈H,对于任何x∈H,路径提升问题有唯一一个定义在最大开区间Ix=(t-x,t+x),-∞≤t-x,t+x≤+∞上的连续解t→γx(t),并且集合{(x,t)∈H×R:t∈Ix}是H×R上的开集,映射(x,t)→γx(t)是连续的.
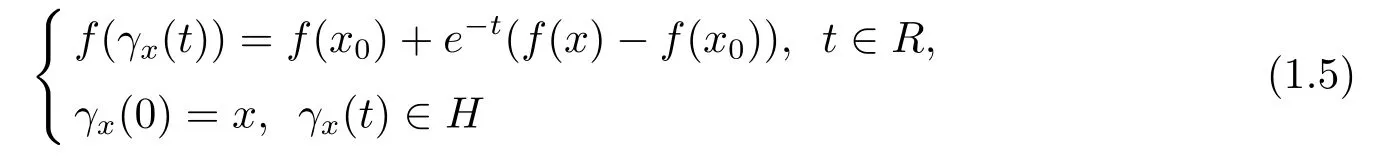
定义1.1[6]在引理1.1的假设条件下,x0的吸引盆是指集合B={x∈H:t+x=+∞}.
定理1.1[8]设连续映射f:H⊂E→F是局部同胚的,则f是全局同胚的充要条件是对所有的x∈B,γx(t)都定义在实数R上,即γx(t)可以向-∞延伸.
2 一些不等式
在这一部分,将推导一些重要的不等式,它们在主要定理的证明中起着重要作用.考虑二阶抛物算子

其中a(x)是t,x1,···,xn的有界函数.设W0(D)是以
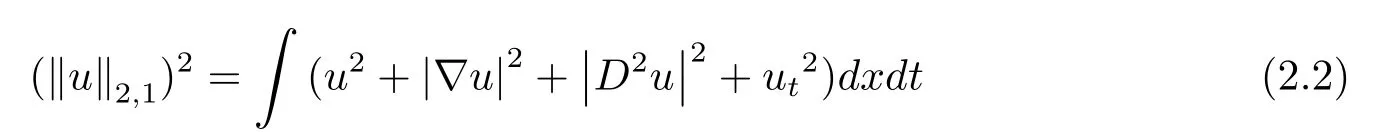
为范数的Hilbert空间,其中梯度是相对于空间变量,并且u∈W0(D)意味着u是定义在D=Ω×[0,T]中的;Ω是紧的有界集,其边界分段光滑且处处有非负平均曲率;|D2u|2表示关于空间变量的所有二阶导数的平方和.
记

(2.1)式可以写为

根据上述假设可得L0是一个由W0(D)映入L2(D)的线性算子.


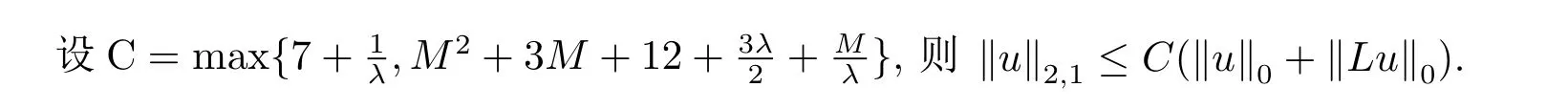
3 主要定理
下面给出方程

满足初始条件u(x,0)=0,(x,t)∈∂Ω×(0,T)的解的存在性和唯一性的充分条件.
设∂Ω∈C2,对于所有的(x,t),h关于u连续,且对于所有的u,h关于(x,t)可测,且有直到三阶连续偏导数.
将式(3.1)改写为算子形式

于是式(3.1)等价于

求Frechet导数,于是对一切u,φ∈W0(D),有
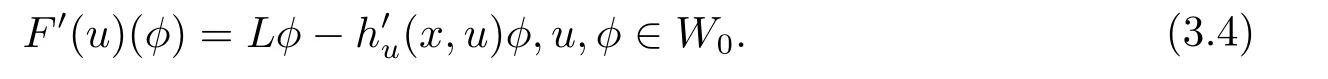
定理3.1假设


[1]Elcrat A R,Sigillito V G.An explicit a priori estimate for parabolic equations with applications to semilinear equations[J].J.Math.Anal.,1976,7(3):746-753.
[2]Chen P J,Gurtin M E.On a theory of heat conduction involving two temperatures[J].Z.Angew. Math.Phys.,1968,19(4):614-627.
[3]Sigillito V G.Pointwise bounds for solutions of semilinear parabolic equations[J].SIAM J.Appl. Math.,1967,9(3):581-585.
[4]Sigillito V G.On a continuous method of approximating solutions of the heat equation[J].J.Assoc. Comp.Mach.,1967,14(4):732-741.
[5]Feng Y Q,Wang Z Y.The application of the basin of attraction to the existence and uniqueness of solutions for the second order parabolic boundary value problem[J].J.Math.,2016,36(5):949-954.
[6]Gorni G.Acriterion of invertibility in the large for local dif f eomorphisms between Banach spaces[J]. Nonl.Anal.,1993,21(1):43-47.
[7]Plastock R.Homeomorphism between Banach space[J].Trans.Am.Math.Soc.,1974,200:169-183.
[8]Wang W X,Shen Z H.The basin of attraction in Banach spaces and its applications[J].Acta Math. Sinica Chin.Ser.,2006,49(5):1013-1020.
[9]Ladyzhenskaya O A,Uraltseva N N.Linear and quasiliear elliptic equation[M].New York:Academic Press,1968.
[10]Elcrat A R.Constructive existence for semilinear eliptic equations with discontinuous coefficients[J]. SIAM J.Math.Anal.,1974,5(4):663-672.
[11]Feng Y Q,Wang Z Y,Wen C J.Global homeomorphism and applications tothe existence and uniqueness of solutions ofsome dif f erential equations[J].Adv.Dif f.Equ.,2014:52,DOI:10.1186/1687-1847-2014-52.
A EXISTENCE THEOREM FOR SOME SECOND ORDER PARABOLIC INITIAL-BOUNDARY VALUE PROBLEMS
FENG Yan-qing,WANG Zong-ying,YAO Jun,WEN Chuan-jun
(School of Mathematics and Chemical Engineering,Changzhou Institute of Technology, Changzhou 213000,China)
In this paper,an a priori estimate for a second order linear parabolic operators is established.By using the basin of attraction and homeomorphism,a new sufficient condition of the existence and uniqueness of an initial boundary value problem for a second order parabolic equations is proved.This idea can be applied some semi-linear partial dif f erential equations.
second order parabolic equation;initial-boundary value problem;the basin of attraction;homeomorphism
O175
A
0255-7797(2017)05-1075-06
2016-12-01接收日期:2017-03-08
冯艳青(1969-),女,浙江义乌,教授,主要研究方向:微分方程及数值解.
2010 MR Subject Classif i cation:35K05;35K20
- 数学杂志的其它文章
- 具有相依理赔量的离散时间风险模型的破产问题
- COMPLETE CONVERGENCE FOR ARRAYS OF ROWWISE M-NSD RANDOM VARIABLES
- OSCILLATION OF NONLINEAR IMPULSIVE DELAY HYPERBOLIC EQUATION WITH FUNCTIONAL ARGUMENTS VIA RICCATI METHOD
- 偏微分方程边值反问题的数值方法研究
- A CLASS OF PROJECTIVELY FLAT SPHERICALLY SYMMETRIC FINSLER METRICS
- 奇异高阶积分边值问题正解的全局结构

