线性空间中代数广义逆的最简表示
郭志荣,黄强联,张莉
(1.扬州大学数学科学学院,江苏扬州225002)
(2.扬州职业大学数学学院,江苏扬州225009)
线性空间中代数广义逆的最简表示
郭志荣1,2,黄强联1,张莉1
(1.扬州大学数学科学学院,江苏扬州225002)
(2.扬州职业大学数学学院,江苏扬州225009)
本文主要在一般线性空间框架中从纯代数的角度研究代数广义逆的可加性与表示问题.首先在线性空间中利用空间代数直和分解给出I+AT+可逆的充要条件,进而T+=T+(I+AT+)-1,给出了具有最简表示的一系列充要条件.其次讨论了在Banach空间广义逆和Hilbert空间Moore-Penrose逆扰动问题研究中的应用.本文的主要结果推广和改进了相关文献中的一些近期成果.
代数广义逆;广义逆;Moore-Penrose逆;最简表示;线性空间
1 引言及预备知识
设X,Y为线性空间,L(X,Y)表示从X到Y中的线性算子的全体.对T∈L(X,Y), D(T),N(T)和R(T)分别表示算子T的定义域,核空间和值域.I表示恒等算子.设M,N为X的线性子空间,M˙+N表示M与N的代数直和.若X,Y为Banach空间,M和N为X的闭子空间,M⊕N表示M与N的拓扑直和.B(X,Y),C(X,Y)分别表示从X到Y中的有界线性算子组成的Banach空间和稠定闭算子全体构成的齐次集.
定义1.1[1,2]设X,Y为线性空间,T∈L(X,Y).若S∈L(Y,X)满足R(T)⊆D(S), R(ST)⊆D(T),且TST=T,则称S为T的代数内逆;若S满足R(S)⊆D(T),R(TS)⊆D(S),且STS=S,则称S为T的代数外逆.若S既是T的代数内逆,又是T的代数外逆,则称S为T的代数广义逆,记作T+.
代数广义逆与空间的代数直和分解是一一对应的[3],其不涉及空间的拓扑结构.在Banach空间或Hilbert空间中,对应于不同的拓扑结构,可以引入相应的广义逆.
定义1.2[3]设X,Y为Banach空间,T∈B(X,Y).若S∈B(Y,X)满足TST=T,则称S为T的内逆;若S满足STS=S,则称S为T的外逆.若S既是T的内逆,又是T的外逆,则称S为T的广义逆,仍记作T+.
Banach空间的广义逆与空间的拓扑直和分解对应,即
定理1.3[4]T+∈B(Y,X)为算子T∈B(X,Y)的广义逆当且仅当X,Y分别具有拓扑直和分解,X=N(T)⊕R(T+),Y=R(T)⊕N(T+).
定义1.4[3]若X,Y为Hilbert空间,定理1.3中的分解为正交分解,则称相应的广义逆为T的Moore-Penrose逆,记为T†.
定义1.5[5]设X,Y为Banach空间,T∈C(X,Y).若算子S∈C(Y,X)满足R(S)⊆D(T),R(T)⊆D(S),且在D(T)上TST=T;在D(S)上STS=S,则称S为T的(无界)广义逆,仍记作T+.
定理1.6[3]设X,Y为Banach空c间,T∈C(X,Y),N(T)和R(T)的闭包R(T)分别在X,Y中存在拓扑补N(T)c和R(T),即

记P,Q分别为X沿N(T)c到N(T)上和Y沿R(T)c到R(T)上的投影算子,则存在唯一的算子S∈C(Y,X)满足:1)在D(T)上TST=T;2)在D(S)上ScTS=S;3)在D(T)上ST=I-P和4)在D(S)上TS=Q,其中D(S)=R(T)+R(T).进一步,S有界当且仅当R(T)在Y中闭.
根据定理1.6,在空间具有拓扑直和分解(1.1)的条件下,T存在无界广义逆.又若X,Y为Hilbert空间,(1.1)中的分解为正交分解,则称相应的广义逆为T的Moore-Penrose逆,记为T†.
广义逆扰动理论是广义逆理论研究的核心内容之一,在近代分析、计算、优化与控制论等学科中有着广泛而重要的应用[3,4,6-8].广义逆扰动理论主要研究算子经过微小扰动后是否仍然存在广义逆,若不存在,什么条件可以保证存在;若存在,能否给出其表达式或广义逆是否(在某种意义下)收敛于原广义逆.国内外很多学者研究了Banach空间中的各种线性算子广义逆和Hilbert空间中Moore-Penrose逆的表示与扰动问题[3,6,7,9-18],如
定理1.7[7]设X,Y为Banach空间,T∈B(X,Y)存在广义逆T+∈B(Y,X), δT∈B(X,Y)满足kδTT+k<1.则下列命题等价
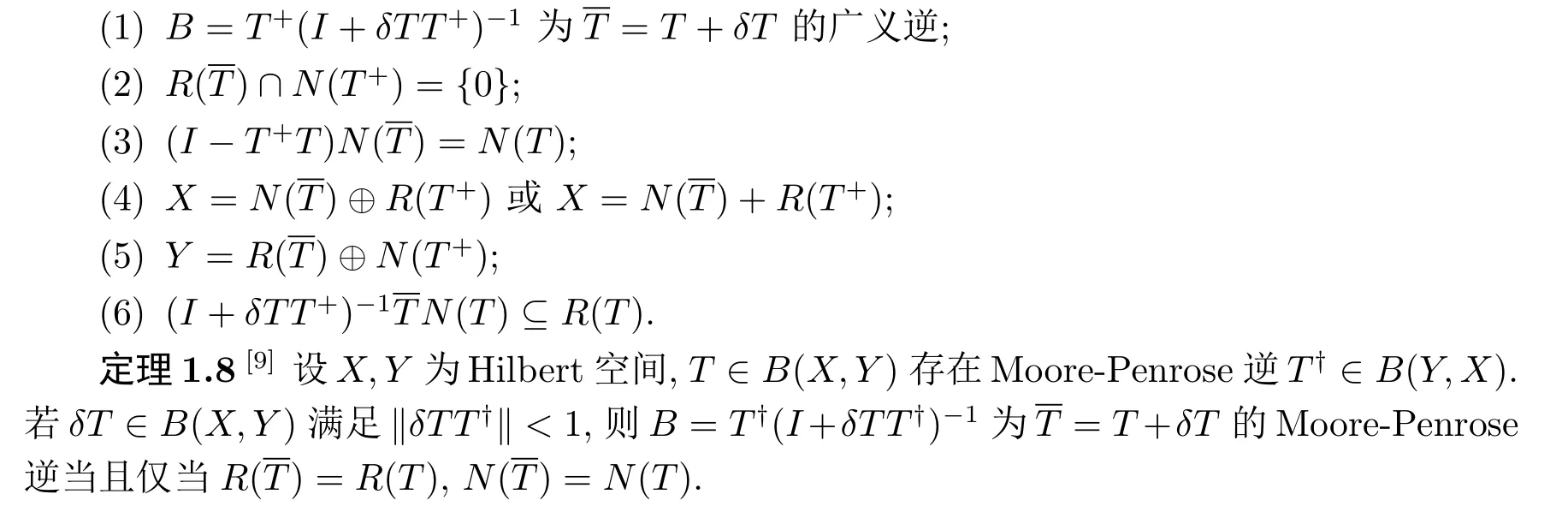
无论是在Banach空间或Hilbert空间,讨论有界线性算子或稠定闭算子的广义逆或Moore-Penrose逆的扰动表示问题,本质上都是讨论线性空间中代数广义逆的可加性问题.因而,在一般线性空间框架中从纯代数的角度讨论代数广义逆更具有一般性.在1974年, Nashed和Votruba就在其系列论文中从纯代数的角度研究了线性空间中代数内逆、代数外逆、代数广义逆及其性质[1,2,3].代数广义逆与Banach空间中的广义逆不同,最本质的区别在于代数广义逆不涉及空间的拓扑.由于子空间在线性空间中总是代数可补,因而代数广义逆总是存在的[3].一个自然的问题是什么条件能保证代数广义逆唯一?能否给出相应广义逆的具体表达式?本文拟从纯代数角度给出代数广义逆的最简形式的表示,主要结果推广和改进了文[6,7,9,12-16,18]中的相关结果.
2 主要结果
引理2.1设T∈L(X,Y),S∈L(Y,X)满足R(S)⊆D(T),R(T)⊆D(S).若S为T的代数外逆,则下列命题等价
(1)S为T的代数广义逆;
(2)R(T)=R(TS);
(3)D(S)=R(T)˙+N(S);
(4)R(T)∩N(S)={0};
(5)N(ST)=N(T);
(6)D(T)=R(S)˙+N(T)或D(T)=R(S)+N(T).
证由于S为T的代数外逆,则TS,ST均为幂等算子,且R(S)=R(ST),N(TS)= N(S),D(T)=R(ST)˙+N(ST)=R(S)˙+N(ST),D(S)=R(TS)˙+N(TS)=R(TS)˙+N(S).
(1)⇒(2)若S为T的代数广义逆,则TST=T,从而R(T)=R(TST)⊆R(TS)⊆R(T).
(2)⇒(3)若R(T)=R(TS),则D(S)=R(TS)˙+N(S)=R(T)˙+N(S).
(3)⇒(4)显然.
(4)⇒(1)对任意x∈D(T),S(TSTx-Tx)=STSTx-STx=STx-STx=0,从而TSTx-Tx∈N(S).又TSTx-Tx∈R(T),根据(4),则TSTx=Tx.故TST=T.因此, S为T的代数广义逆.
(1)⇒(5)若S为T的代数广义逆,则TST=T.如果STx=0,那么Tx=TSTx=0,即N(ST)⊆N(T),又显然有N(T)⊆N(ST)成立.故N(ST)=N(T).
(5)⇒(6)若N(ST)=N(T),则D(T)=R(S)˙+N(ST)=R(S)˙+N(T).
(6)⇒(1)对任意x∈D(T),由(6),存在y∈D(S)和x1∈N(T),使得x=Sy+x1.从而TSTx=TST(Sy+x1)=TSTSy=TSy=T(Sy+x1)=Tx.故TST=T,从而S为T的代数广义逆.证毕.
引理2.2设T+∈L(Y,X)为T∈L(X,Y)的代数广义逆,A∈L(X,Y)满足D(T)⊆D(A),R(T+)⊆D(A),R(A)⊆D(T+).若T=T+A,则下列命题等价
(1)I+AT+:D(T+)→D(T+)为双射;
(2)I+T+A:D(T)→D(T)为双射;
(3)N(T)∩R(T+)={0}和D(T+)=TR(T+)+˙N(T+).
证(1)⇒(2)先证I+T+A:D(T)→D(T)为单射.若x∈D(T),(I+T+A)x=0,则A(I+T+A)x=0,即(I+AT+)Ax=0.根据(1),Ax=0,从而x=-T+Ax=0.次证I+T+A:D(T)→D(T)为满射,也就是需证对任意y∈D(T),存在x∈D(T)使得(I+T+A)x=y.事实上,由于Ay∈D(T+),由(1),存在h∈D(T+),满足(I+AT+)h=Ay.令x=y-T+h,则x∈D(T),且
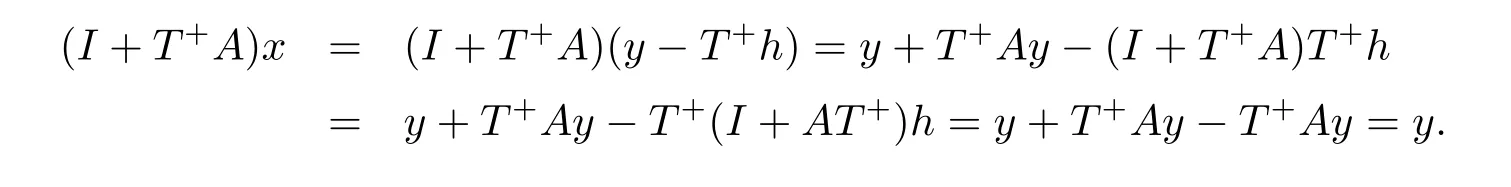
(2)⇒(3)若I+T+A:D(T)→D(T)为双射.设y∈N(T)∩R(T+),则存在x∈D(T+),满足y=T+x,TT+x=Ty=0.因此
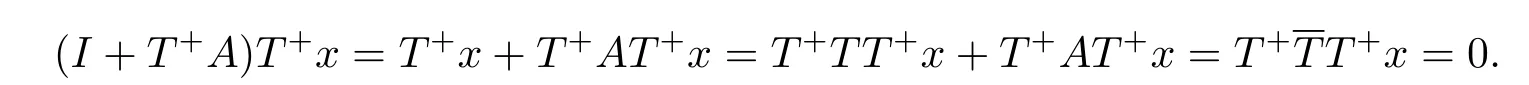
故T+x=0,即y=T+x=0.从而N(T)∩R(T+)={0}.下面证TR(T+)∩N(T+)={0}.设v∈TR(T+)∩N(T+),则存在u∈D(T+),满足v=TT+u.因此
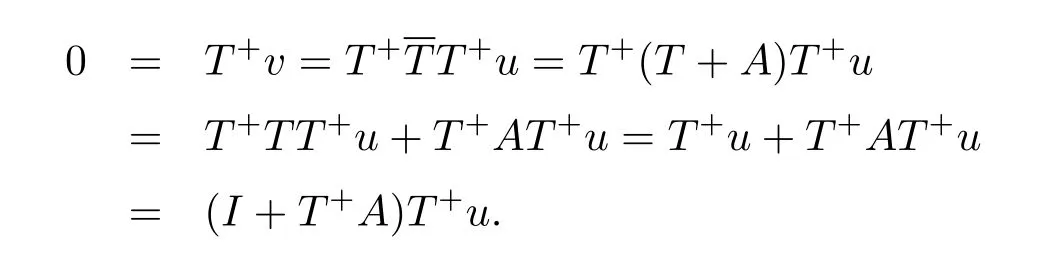
那么T+u=0,v=TT+u=0.
最后证D(T+)=TR(T+)+N(T+).一方面,易见TR(T+)+N(T+)⊆D(T+).另一方面,任取x∈D(T+),T+x∈D(T).根据(2),存在y∈D(T),使得T+x=(I+T+A)y,即T+x=(I-T+T)y+T+Ty.从而
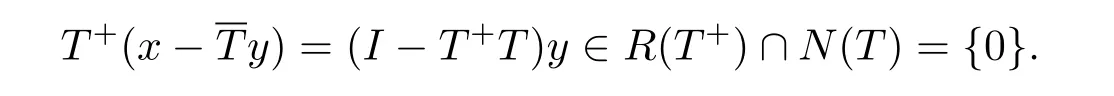
因此y=T+Ty∈R(T+),T+x=T+Ty,进而x-Ty∈N(T+).则

故D(T+)=TR(T+)+N(T+).
(3)⇒(1)首先证明I+AT+:D(T+)→D(T+)为单射.事实上,若x∈D(T+)满足(I+AT+)x=0,则TT+x=TT+x-x∈TR(T+)∩N(T+)={0},从而x=TT+x,TT+x= 0.故T+x∈N(T)∩R(T+),根据(3),T+x=0.因此x=TT+x=0.为完成证明,只需证I+AT+:D(T+)→D(T+)为满射.对任何y∈D(T+),由于D(T+)=TR(T+)+N(T+), y能表示为y=TT+y1+y2,其中y1∈D(T+),y2∈N(T+).因此
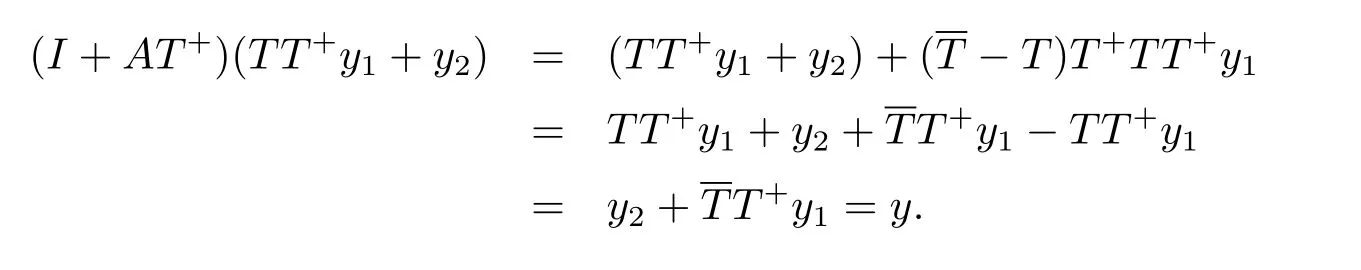
故I+AT+:D(T+)→D(T+)为双射.证毕.
下面的定理说明如果T的代数广义逆T+保持T的代数广义逆T+的定义域,值域和核空间,那么T+是唯一确定的,并且具有最简表示形式.
定理2.3设T+∈L(Y,X)为T∈L(X,Y)的代数广义逆,A∈L(X,Y)满足D(T)⊆D(A),R(T+)⊆D(A),R(A)⊆D(T+).若T=T+A存在代数广义逆T+∈L(Y,X),满足
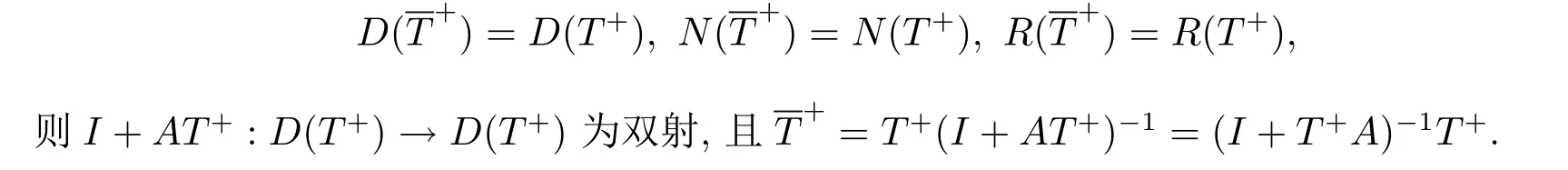
证由于T+为T的代数广义逆,则N(T)∩R(T+)={0}和D(T+)=R(T T+)+˙N(TT+) =TR(T+)+˙N(T+).因此根据假设,得到N(T)∩R(T+)={0},D(T+)=TR(T+)+˙N(T+).由引理2.2,I+AT+:D(T+)→D(T+)和I+T+A:D(T)→D(T)均为双射.进一步可验证T+(I+AT+)-1和(I+T+A)-1T+均是可定义的,且
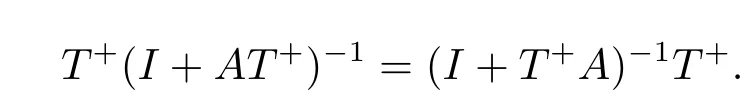
又由N(T+)=N(T+)和T+(I-TT+)=0及R(T+)=R(T+)和(I-T+T)T+=0可知, T+=T+TT+和T+TT+=T+.故T++T+TT+-T+TT+=T+,从而T+(I+AT+)=T+.因此,T+=T+(I+AT+)-1.证毕.
下面给出T+具有最简表示形式T+=T+(I+AT+)-1的充要条件.
定理2.4设T+∈L(Y,X)为T∈L(X,Y)的代数广义逆,A∈L(X,Y)满足D(T)⊆D(A),R(T+)⊆D(A),R(A)⊆D(T+).若I+AT+:D(T+)→D(T+)为双射,则下列命题等价
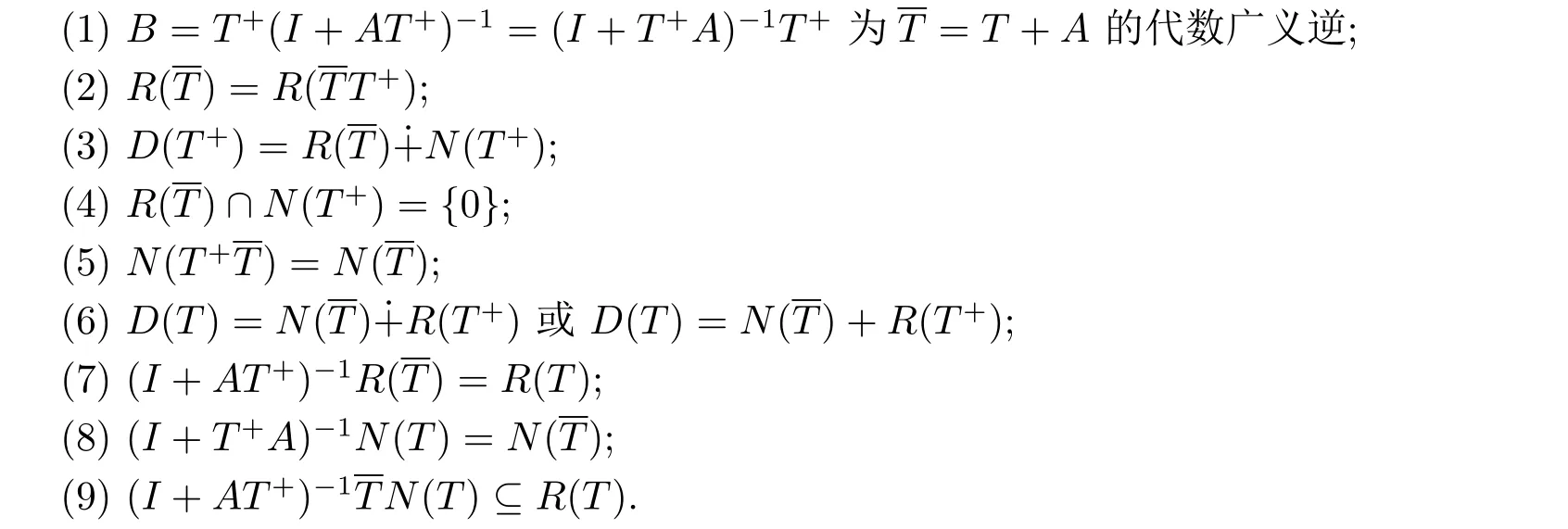
证易见B=T+(I+AT+)-1=(I+T+A)-1T+是可定义的,且R(B)=R(T+), N(B)=N(T+).因为
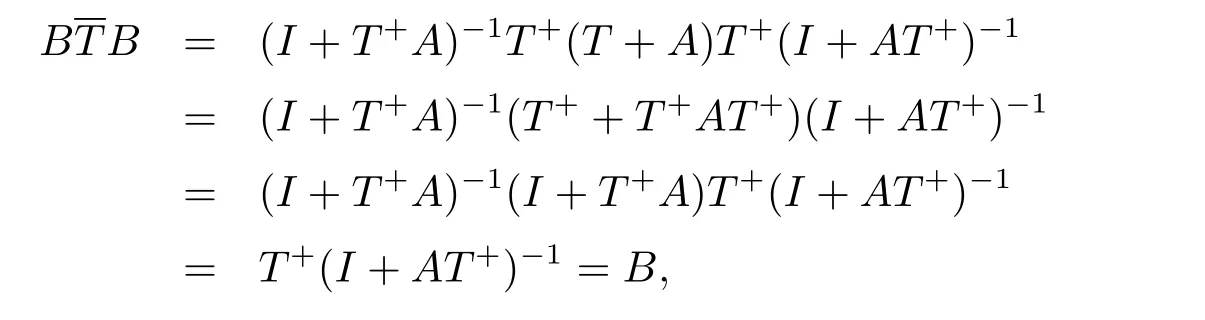
所以B为T的代数外逆.注意到R(TB)=R(TT+)和N(BT)=N(T+T),根据引理2.1,我们知(1)~(6)两两等价.
(1)⇒(7)若B为T的广义逆,则
(7)⇒(8)显然,(I+T+A)N(T)=[I+T+(T-T)]N(T)=(I-T+T)N(T)⊆N(T).另一方面,由(7),对任何x∈N(T),有
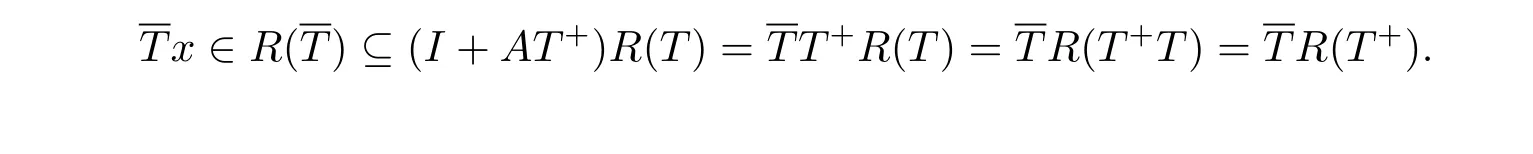
故存在y∈R(T+),使得Ty=Tx.那么x-y∈N(T),且
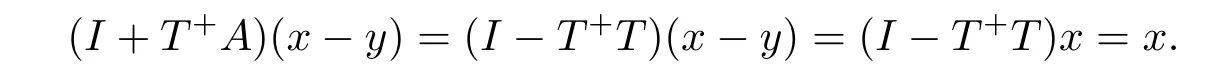
因此N(T)⊆(I+T+A)N(T).
(8)⇒(4)任取y∈R(T)∩N(T+),存在x∈D(T),满足y=Tx和T+Tx=0.因而

即(I+T+A)x∈N(T).根据(8),x∈N(T),故y=Tx=0.
(7)⇒(9)显然.
(9)⇒(4)设y∈R(T)∩N(T+),存在x∈D(T)=D(T)满足y=Tx和T+Tx=0.因为D(T)=N(T)+˙R(T+),x=x1+x2,这里x1∈N(T),x2∈R(T+).则

因而(I+AT+)-1Tx2=Tx2∈R(T).由(9),(I+AT+)-1Tx1∈R(T).注意到y∈N(T+),我们得到(I+AT+)y=y=Tx,进而
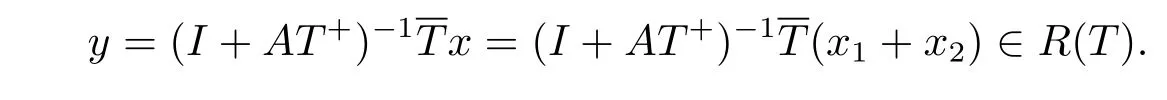
故y∈R(T)∩N(T+).根据R(T)∩N(T+)={0}知,y=0.证毕.
定理2.5设T∈L(X,Y)为有限秩算子,T+∈L(Y,X)为T的代数广义逆,A∈L(X,Y)满足D(T)⊆D(A),R(T+)⊆D(A),R(A)⊆D(T+).若I+AT+:D(T+)→D(T+)为双射,则B=T+(I+AT+)-1=(I+T+A)-1T+为T=T+A的代数广义逆当且仅当
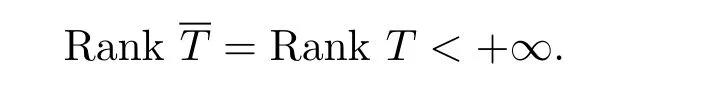
证必要性由定理2.4的(1)⇔(7)可得.下面证明充分性.根据(I+AT+)T= T+AT+T=TT+T,有T=(I+AT+)-1TT+T成立.如果Rank T=Rank T,那么dimR(T)=dimR(T)=dimR(TT+T).因此R(T)=R(TT+T)⊆R(TT+)⊆R(T).再根据定理2.4中的(1)⇔(2),B为T的代数广义逆.证毕.
类似地,可以证明
定理2.6设T+∈L(Y,X)为T∈L(X,Y)的代数广义逆,A∈L(X,Y)满足D(T)⊆D(A),R(T+)⊆D(A),R(A)⊆D(T+).若dimN(T)<+∞,I+AT+:D(T+)→D(T+)为双射,则B=T+(I+AT+)-1=(I+T+A)-1T+为T=T+A的代数广义逆,当且仅当
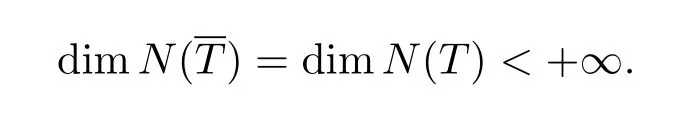
3 应用
作为进一步的应用,本节讨论Banach空间中广义逆和Hilbert空间中Moore-Penrose逆的扰动表示.首先由定理2.4,可以得到
定理3.1设X,Y为Banach空间,T∈C(X,Y)存在广义逆T+∈C(Y,X),δT∈B(X,Y)满足R(δT)⊆D(T+).若kT+δTk<1,则下列命题等价

证根据T∈C(X,Y)与δT∈B(X,Y),T=T+δT为稠定闭算子.又在假设<1下,由著名的Banach引理,I+T+δT:X→X可逆,且(I+T+δT)-1为有界线性算子.由T+为稠定闭算子,容易证明B=(I+T+δT)-1T+也为稠定闭算子.根据定理2.4知,结论成立.证毕.
定理3.2设X,Y为Banach空间,T∈C(X,Y)存在有界广义逆T+∈B(Y,X).若δT∈B(X,Y)满足kδTT+k<1,则下列命题等价
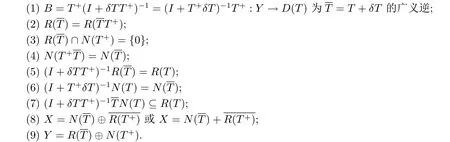
证在假设kδTT+k<1下,I+δTT+:Y→Y可逆,且(I+δTT+)-1为有界线性算子.易见B=T+(I+δTT+)-1为有界线性算子.若B为T的广义逆,则根据定理1.6和定理2.4,(2)~(9)均成立.反之,若(2)~(7)中之一成立,则(1)成立.若(9)成立,则(3)成立.若X=N(T)+R(T+)成立,则对任何x∈N(T),存在x1∈N(T),x2∈R(T+),使得x=x1+x2.从而x2=x-x1∈D(T),且x2-T+Tx2∈R(T+)∩N(T)={0},即x2=T+Tx2.因此
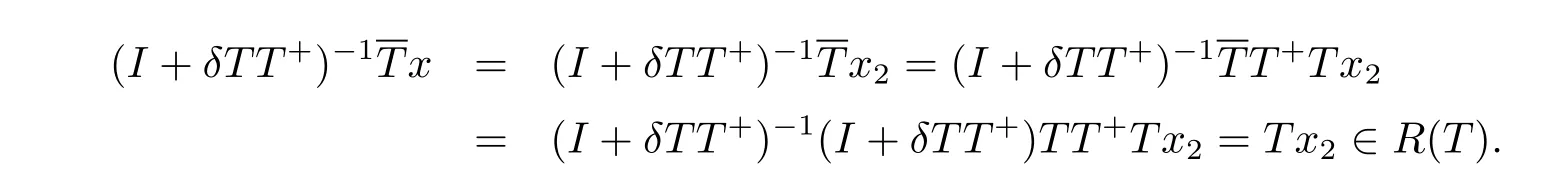
故(7)成立.证毕.
当T∈B(X,Y),T+∈B(Y,X)时,R(T+)为闭集.由定理3.2,直接可以得到
定理3.3设X,Y为Banach空间,T∈B(X,Y)存在广义逆T+∈B(Y,X).若δT∈B(X,Y)满足kδTT+k<1.则下列命题等价
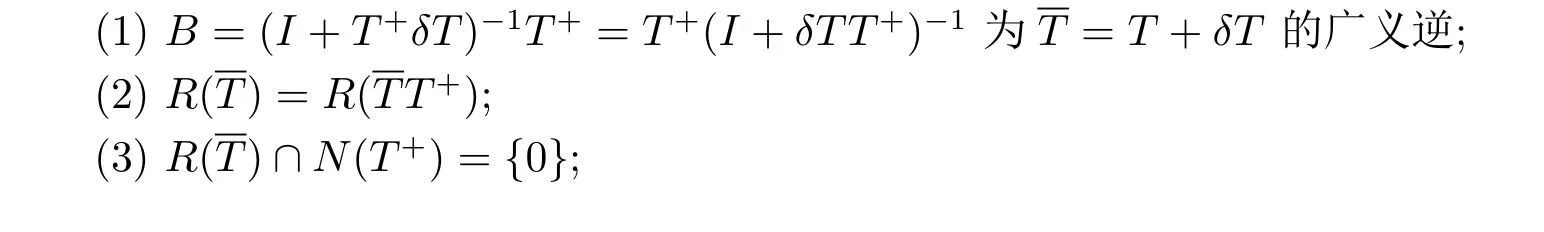

注定理3.2和定理3.3推广了文[6,7,13-16,18]中的相关结果.
定理3.4设X,Y为Hilbert空间,T∈C(X,Y)存在Moore-Penrose逆T†∈B(Y,X).若δT∈B(X,Y)满足kδTT†k<1,则B=T†(I+δTT†)-1=(I+T†δT)-1T†为T=T+δT的Moore-Penrose逆当且仅当R(T)=R(T),N(T)=N(T).
证若R(T)=R(T),N(T)=N(T)成立,则根据定理3.2,B为T的广义逆.因此
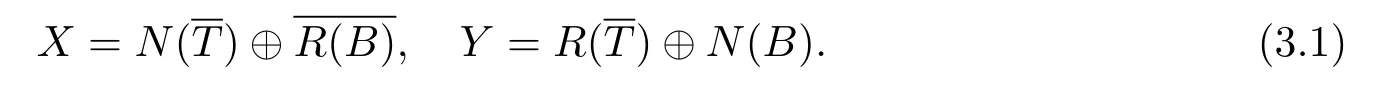
根据Moore-Penrose逆的定义,X与Y分别具有正交分解
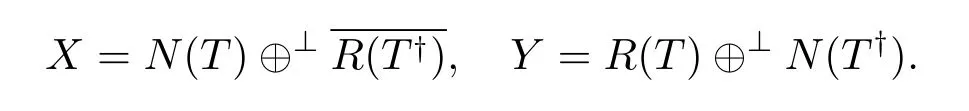
又R(T†)=R(B),N(T†)=N(B),则X=N(T)⊕⊥R(B),Y=R(T)⊕⊥N(B),即(3.1)式中的拓扑分解为正交分解.因此B为T的Moore-Penrose逆.反之,若B为T的Moore-Penrose逆,则

从而N(T)=R(B)⊥,R(T)=N(B)⊥.注意到N(T)=R(T†)⊥,R(T)=N(T†)⊥,R(T†)= R(B)和N(T†)=N(B),我们得到R(T)=R(T)和N(T)=N(T).证毕.
注定理3.4推广了文[9,14-16]中的相关结果.
[1]Nashed M Z,Votruba G F.A unif i ed approach to generalized inverses of linear operators:I.Algebraic,topological,and projectional properties[J].Bull.Amer.Math.Soc.,1974,80(5):825-830.
[2]Nashed M Z,Votruba G F.A unif i ed approach to generalized inverses of linear operators:II. Extremal and proximal properties[J].Bull.Amer.Math.Soc.,1974,80(5):831-834.
[3]Nashed M Z.Generalized inverses and applications[M].New York:Academic Press,1976.
[4]王玉文.巴拿赫空间中算子广义逆理论及其应用[M].北京:科学出版社,2005.
[5]Ben-Israel A,Greville T N E.Generalized inverses:theory and applications(2nd ed.)[M].New York:Wiley,2003.
[6]Chen G L,Xue Y F.Perturbation analysis for the operator equation Tx=b in Banach spaces[J]. J.Math.Anal.Appl.,1997,212(1):107-125.
[7]Ma J P.Complete rank theorem of advanced calculus and singularities of bounded linear operators [J].Front.Math.China,2008,3(2):305-316.
[8]Nashed M Z.Inner,outer,and generalized inverses in Banach and Hilbert spaces[J].Numer.Funct. Anal.Optim.,1987,9(3):261-325.
[9]Ding J.On the expression of generalized inverses of perturbed bounded linear operators[J].Missouri J.Math.Sci.,2003,15(1):40-47.
[10]Du N L.The basic principles for stable approximations to orthogonal generalized inverses of linear operators in Hilbert spaces[J].Numer.Funct.Anal.Optim.,2005,26(6):675-708.
[11]Du N L.Finite-dimensional approximation settings for inf i nite-dimensional Moore-Penrose inverses [J].SIAM J.Numer.Anal.,2008,46(3):1454-1482.
[12]黄强联,马吉溥,王丽.Banach空间中闭线性算子广义预解式存在定理[J].数学年刊,2011,32A(5):635-646.
[13]Huang Q L,Zhai W X.Perturbations and expressions for generalized inverses in Banach spaces and Moore-Penrose inverses in Hilbert spaces of closed linear operators[J].Linear Algebra Appl.,2011, 435(1):117-127.
[14]Huang Q L,Zhu L P,Geng W H,Yu J N.Perturbation and expression for inner inverses in Banach spaces and its applications[J].Linear Algebra Appl.,2012,436(9):3715-3729.
[15]Huang Q L,Zhu L P,Jiang Y Y.On the stable perturbation of outer inverses of linear operators in Banach spaces[J].Linear Algebra Appl.,2012,437(7):1942-1954.
[16]Wang Y W,Zhang H.Perturbation analysis for oblique projection generalized inverses of closed linear operators in Banach spaces[J].Linear Algebra Appl.,2007,426(1):1-11.
[17]Xu Q X,Song C N,Wei Y M.The stable perturbation of the Drazin inverse of the square matrices [J].SIAM J.Matrix Anal.Appl.,2009,31(3):1507-1520.
[18]Yang X D,Wang Y W.Some new perturbation theorems for generalized inverses of linear operators in Banach spaces[J].Linear Algebra Appl.,2010,433(11):1939-1949.
THE SIMPLEST EXPRESSION OF THE ALGEBRAIC GENERALIZED INVERSES IN LINEAR SPACES
GUO Zhi-rong1,2,HUANG Qiang-lian1,ZHANG Li1
(1.School of Mathematical Sciences,Yangzhou University,Yangzhou 225002 China)
(2.College of Mathematics,Yangzhou Vocational University,Yangzhou 225009 China)
In this paper,the authors study the additivity and expression of algebraic generalized inverses from the view of pure algebra in the framework of linear space.Utilizing the algebraic direct sum decomposition of linear space,we fi rst give the necessary and sufficient condition of the invertibility of I+AT+and T+=T+(I+AT+)-1.We also provide some necessary and sufficient conditions for T+to have the simplest expression.As applications,we discuss the perturbation problem of generalized inverse in Banach space and Moore-Penrose inverse in Hilbert space,which extend and improve many recent results in this topic.
algebraic generalized inverse;generalized inverse;Moore-Penrose inverse;the simplest expression;linear space
O177.2
A
0255-7797(2017)05-1013-09
2017-03-10接收日期:2017-06-02
国家自然科学基金资助(11771378;11271316);江苏省自然科学基金资助(BK20141271);扬州大学中青年学术带头人基金资助(2016zqn03).
郭志荣(1970-),男,江苏扬州,副教授,主要研究方向:泛函分析.
黄强联.
2010 MR Subject Classi fi cation:47L05;46A32
- 数学杂志的其它文章
- 具有相依理赔量的离散时间风险模型的破产问题
- COMPLETE CONVERGENCE FOR ARRAYS OF ROWWISE M-NSD RANDOM VARIABLES
- OSCILLATION OF NONLINEAR IMPULSIVE DELAY HYPERBOLIC EQUATION WITH FUNCTIONAL ARGUMENTS VIA RICCATI METHOD
- 偏微分方程边值反问题的数值方法研究
- A CLASS OF PROJECTIVELY FLAT SPHERICALLY SYMMETRIC FINSLER METRICS
- 奇异高阶积分边值问题正解的全局结构

