AVERAGING FOR MEASURE FUNCTIONAL DIFFERENTIAL EQUATIONS WITH INFINITE DELAY

LI Bao-lin,WANG Bao-di

(College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,China)

AVERAGING FOR MEASURE FUNCTIONAL DIFFERENTIAL EQUATIONS WITH INFINITE DELAY

LI Bao-lin,WANG Bao-di

(College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,China)

In this paper,we study the averaging for measure functional dif f erential equations with inf i nite delay.By using the averaging theorem for generalized ordinary dif f erential equations, under the measure functional dif f erential equations with inf i nite delay is equivalent to the generalized ordinary dif f erential equations under some conditions,the periodic and non-periodic averaging theorem for this class of retarded functional dif f erential equations is obtained,which generalizes some related results.

averaging methods;measure functional dif f erential equations;generalized ordinary dif f erential equations;Kurzweil-Stieltjes integral

1 Introduction

In paper[4],the authors stated very nice stability results of measure functional differential equations with inf i nite delay,especially proved that measure functional dif f erential equations with inf i nite delay is equivalent to the generalized ordinary dif f erential equations under some conditions.In[5]and[8],the authors described the averaging methods for generalized ordinary dif f erential equations and there were many sources described the averaging methods for ordinary dif f erential equation,such as[5,8,9].

In the present paper,we establish an averaging result for measure functional dif f erential equations with inf i nite delay.This theorems is based on the averaging method for ordinary dif f erential equations,then we consider the classical averaging theorems for ordinary equations are concerned with the initial-value problem

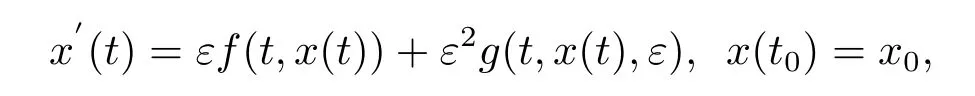
where ε＞0 is a small parameter.Assume that f is T-periodic in the f i rst argument,then we can obtain an approximate of this initial-value problem by neglecting the ε2-term andtaking the averaging of f with respect to t,i.e,we consider the equation

The proof of periodic averaging theorem,which can be traced back to paper[1,2]or[3].

Now,we consider the measure dif f erential equations.

Have a system described by ordinary dif f erential equation

is acted upon by perturbation,the perturbed system is generally given by ordinary di ff erential equation of the form=f(t,x)+G(t,x).Assume the perturbation term G(t(x))is continuous or integrable and as such the state of the system changes continuously with respect to time.However some system one cannot expect the perturbations to be well-behaved. Such as the perturbations are impulsive.So we have the following equations

where Du denotes the distributional derivative of function u.If u is a function of bounded variation,Du can be identif i ed with a Stieltjes measure and will have the ef f ect of suddenly changing the state of the system at the points of discontinuity of u.In[11],equations of form (1.2)are called measure dif f erential equations.Equation(1.2)have the special case when G was considered by Schmaedeke[11].In order to apply the methods of Riemann-Stieltjes integrals in the subsequent analysis we assumed to be a continuous function of t.In[12], the authors introduce the following functional dif f erential equation

where xtrepresents the restriction of the function x(·)on the interval[m(t),n(t)],m and n being functions with the property m(t)≤n(t)≤t.In this case,the methods of R.S. integrals are unapplicable because of the possibility that G(t,xt)and u(t)may have common discontinuities,and Lebsgue-Stieltjes integrals are therefor used.

Moreover,in[13],a important theorem which was considered as the main contents is as following.

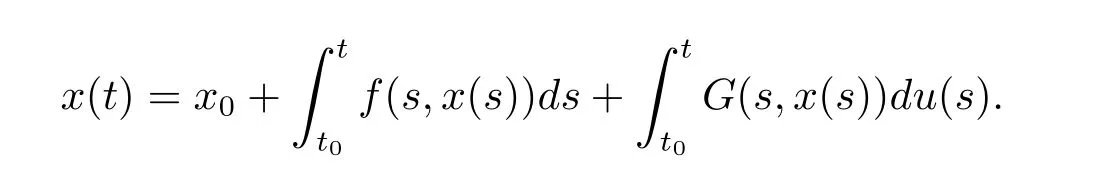
x(·)is a solution of(1.2)through(t0,x0)on an interval I with left end point t0,if and only if x(·)satisf i es the following equationsSo according to the above contents we can arrival at a conclusion measure functional differential equations with delay have the form Dx=G(s,xs)dg(s)is equivalent the following form

In this paper,we shall consider the following initial value problem of measure dif f erential equations

where x is an unknown function with values in Rnand the symbol xsdenotes the function xs(τ)=x(s+τ)def i ned on(-∞,0],which corresponding to the length of the delay.The integral on the right-hand side of(1.4)is the Kurzweil-Stieltjes integral with respect to a nondecreasing function g,where the function f：P×[t0,t0+σ]→Rnand a nondecreasing function g：[t0,t0+σ]→R,where

is a Banach space satisfying conditions(H1)-(H6),t0∈R,σ＞0,O⊂Ht0+σis a space satisfying conditions(1)-(6)of Lemma 2.7,X((-∞,0],Rn)be denoted the set of all regulated functions f：X(-∞,0]→Rn.

Our candidate for the phase space of a measure function dif f erential equations with inf i nite delay is a linear space H0⊂X((-∞,0],Rn)equipped with a norm denoted by k·k⋆.We assume that this normed linear space H0satisf i es the following conditions

(H1)H0is complete.

(H2)If x∈H0and t＜0,then xt∈H0.

(H3)There exist a locally bounded function k1：(-∞,0]→R+such that if x∈H0and t≤0,then k x(t)k≤k1(t)k x k⋆.

(H4)There exist a function k2：(0,∞)→[1,∞)such that if σ＞0 and x∈H0is a function whose support is contained in[-σ,0],then

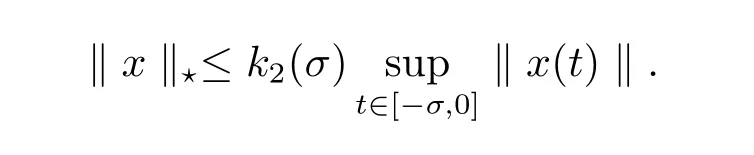
(H5)There exist a locally bounded function k3：(-∞,0]→R+such that if x∈H0and t≤0,then

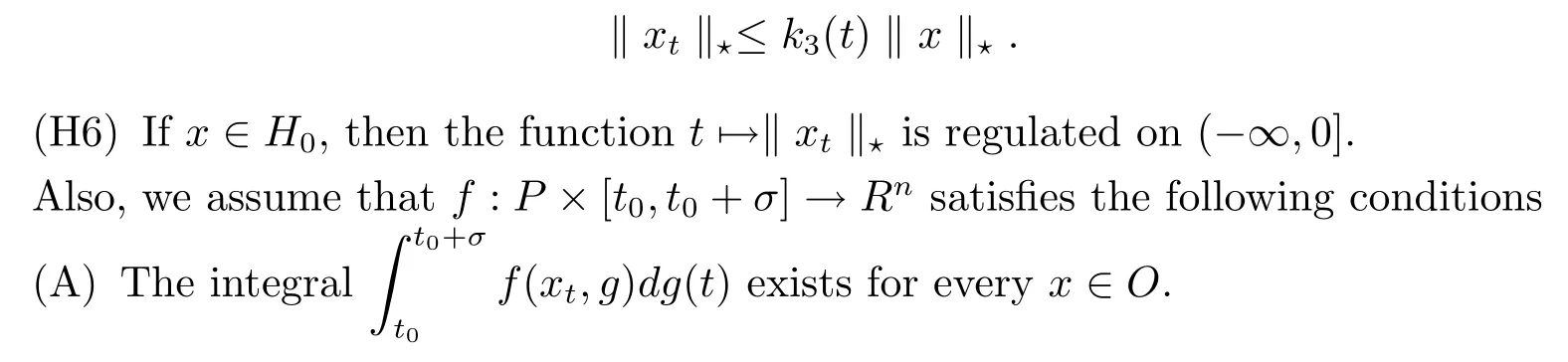
(B)There exists a function M：[t0,to+σ]→R+,which is Kurzweil-Stieltjies integrable with respect to g,such that

whenever x∈O and[a,b]⊆[t0,to+σ].

(C)There exists a function L：[t0,to+σ]→R+,which is Kurzweil-Stieltjies integrable with respect to g,such that

whenever x,y∈O and[a,b]⊆[t0,to+σ](we are assuming that the integral on the right-hand side exists).

In this paper,we using measure functional dif f erential equations with inf i nite delay can translate into generalized oridinary dif f erential equations,this prove is given in paper[4]. According to[5],the f i rst we have a conclusion of periodic averaging theorem for generalized ordinary dif f erential equations.We then show that the classical periodic averaging theorem about measure functional dif f erential equations with inf i nite delay.The next part,according to[8]we have a conclusion of Non-periodic averaging theorem about measure functional dif f erential equations with inf i nite delay.

2 Generalized Ordinary Dif f erential Equations

We start this section with a short summary of Kurzweil integral,which plays a crucial role in the theory of generalized ordinary dif f erential equations.

A function δ：[a,b]→R+.A partition of interval[a,b]with division points a=α0≤α1≤···≤αk=b and tags τi∈[αi-1,αi]is called δ-f i ne if[αi-1,αi]⊂[τi-δ(τi),τi+ δ(τi)],i=1,2,···,k.

A matrix-valued function U：[a,b]×[a,b]→Rn×mis called Kurzweil integrable on [a,b],if there is a matrix I∈Rn×msuch that for every ε＞0,there is a gauge δ on[a,b] such that

Lemma 2.4[6]Let B⊂Rn,Ω=B×[a,b].Assume that F：Ω→Rnbelong to the class F(Ω,h).Then every solution x：[α,β]→B of the generalized ordinary dif f erential equation

is a regulated function.

Lemma 2.5[5]Let B⊂Rn,Ω=B×[a,b].Assume that F：Ω→Rnbelong to the class F(Ω,h).If x,y：[a,b]→B are regulated functions,then

This lemma was proved in[5]Lemma 5.

Lemma 2.6[6]Let h：[a,b]→[0,+∞)be a nondecreasing left-continuous function, k＞0,l≥0.Assume that ψ：[a,b]→[0,+∞)is bounded and satisf i es

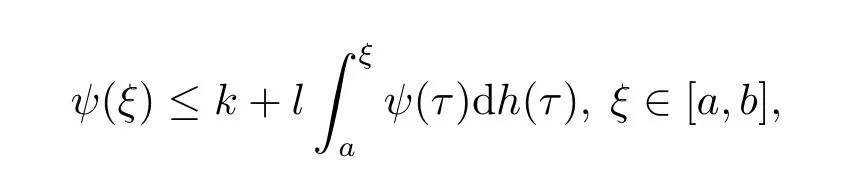
The next Theorem is very important for prove periodic averaging of measure functional dif f erential equation with inf i nite delay.This theorem was proved in[5].

Theorem 2.7[5]Let B⊂Rn,Ω=B×[0,∞],ε0＞0,L＞0.Consider functions F：Ω→Rnand G：Ω×(0,ε0]→Rnwhich satisfy the following conditions

(1)there exist nondecreasing left-continuous functions h1,h2：[0,∞)→[0,∞)such that F belongs to the class F(Ω,h1),and for every f i xed ε∈(0,ε0],the function(x,t)→G(x,t,ε) belongs to the class F(Ω,h2);

(2)F(x,0)=0 and G(x,0,ε)=0 for every x∈B,ε∈(0,ε0];

(3)there exist a number T＞0 and a bounded Lipschitz-continuous function M：B→Rnsuch that F(x,t+T)-F(x,t)=M(x)for every x∈B and t∈[0,∞);

(4)there exist a constant α＞0 such that h1(iT)-h1((i-1)T)≤α for every i∈N;

(5)there exist a constant β＞0 such that

Suppose that for every ε∈(0,ε0].The initial-value problems

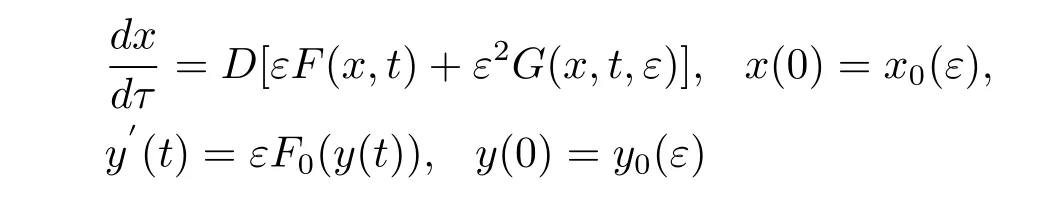
To establish the correspondence between measure functional dif f erential equations and generalized ordinary dif f erential equations,we also need a suitable space Haof regulated functions def i ned on(-∞,a],where a∈R,the next lemma shows that the spaces Hainherit all important properties of H0.

Lemma 2.8[5]If H0⊂G((-∞,0],Rn)is a space satisfying conditions(H1)-(H6), then the following statements are true for every a∈R,

(1)Hais complete.

(2)If x∈Haand t≤a,then xt∈H0.

(3)If t≤a and x∈Ha,then k x(t)k≤k1(t-a)k x k⋆.

(4)If σ＞0 and x∈Ha+σis a function whose support is contained in[a,a+σ],then

(5)If x∈Ha+σand t≤a+σ,thenk xtk⋆≤k3(t-a-σ)k x k⋆.

(6)If x∈Ha+σ,then the function t 7→k xtk⋆is regulated on(-∞,a+σ].

3 Periodic Averaging

In this section,we use Theorem 2.7 to derive a periodic averaging theorem for measure functional dif f erential equations with inf i nite delay.

Theorem 3.1 Given a set H0⊂G((-∞,0],Rn)be a Banach space satisfying conditions (H1)-(H6)t0∈R,σ＞0,O⊂Ht0+σand P={yt：y∈O,t∈[t0,t0+σ]}⊂H0Consider a nondecreasing function u：[t0,t0+σ]→Rnand a function f：P×[t0,t0+σ]→Rn, assume that f is T-periodic and Lipschitz continuous in this argument.Then the measure functional dif f erential equation of the form

is equivalent to a generalized ordinary dif f erential equation of the form

where x takes values in O,and f：O×[t0,t0+σ]→G[-∞,t0+σ]→Rnis given by

for every x∈O and t∈[t0,t0+σ].It will turn out that between the solution x and the solution y is described by

where t∈[t0,t0+σ].

This theorem was proved in[4,Theorem 3.6].

Theorem 3.2 Assume that B⊂Rn,we use the symbol X([a,b],B)to denote the set of all regulated functions f：[a,b]→B.Let ε0＞0,L＞0,Ω=X((-∞,0),B)×[t0,∞) consider a pair of bounded Lipschitz-continuous f：Ω→Rn,g：Ω×(0,ε0]→Rn.Assume that f is T-periodic in the second argument.Def i ne f0：X→Rnby

It follows that F belongs to the class F(X,h1).Similarly,if 0≤s1≤s2and ys,xs∈X that

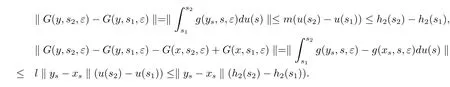
Therefore for every f i xed ε∈(0,ε0],the function(y,s)7→G(y,s,ε)belongs to the class F(X,h2).It is clear that F(y,0)=0 and G(y,0,ε)=0,since u is T-periodic.The function f is T-period in this argument and it follows that dif f erence

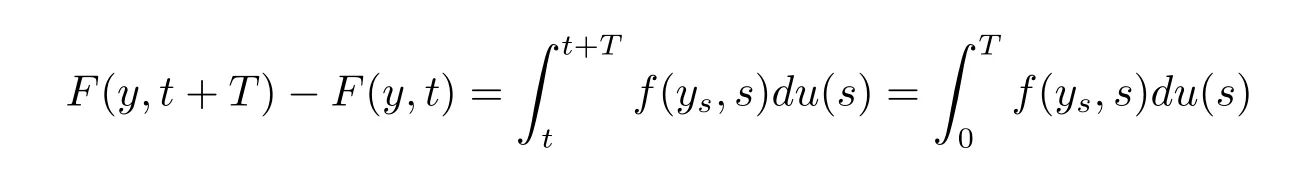
does not depend on t,we can def i ne M(x)=F(y,t+T)-F(y,t).The following calculations show that M is bounded and Lipschitz-continuous

Thus we have checked that all assumptions of Theorem 2.7 are satisf i ed.To conclude the proof,it is now sufficient to def i ne

4 Non-Periodic Averaging

Now we derive non-periodic averaging for measure functional dif f erential equations with inf i nite delay.

Theorem 4.1 Consider a number r＞0 and a function F：X×[0,∞]→Rnsuch that the following conditions are satisf i ed.

1.there exists a nondecreasing function h：[0,∞]→R such that

for every x∈X and s1,s2∈[0,∞];

2.there exists a continuous increasing function ω：[0,∞]→R such that ω(0)=0 and

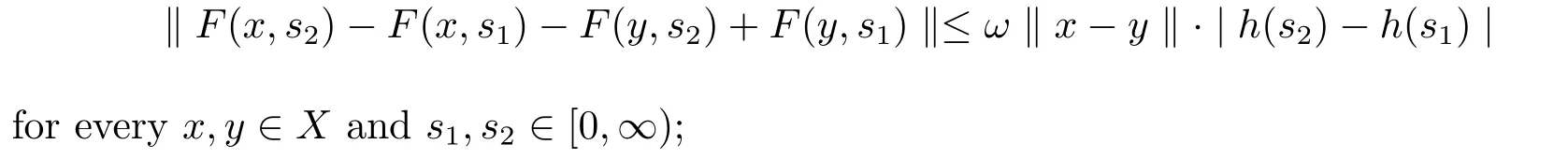
3.there exists a number C∈R such that for every a∈[0,∞],

4.there exists a function F0：X→Rnsuch that

and the ordinary dif f erential equation

Proof According to the assume of Theorem 3.2,there exist constants m,l＞0 such that

[1]Sanders J A,Verhulst F.Averaging methods in nonlinear dynamical systems[M].New York：Springer-Verlag,1985.

[2]Sanders J A,Verhulst F,Murdock J.Averaging methods in nonlinear dynamical systems(2nd ed.)[M].New York：Spring,2007.

[3]Verhulst F.Nonlinear dif f erential equations and dynamical systems(2nd ed.)[M].New York：Spring, 2000.

[4]Slav´ık A.Measure functional dif f erential equations with inf i nite delay[J].Nonl.Anal,2013,79：140-155.

[5]Mesquita J G,Slav´ık A.Periodic averaging theorems for various types of equations[J].J.Math. Ann.Appl.,2012,387：862-877.

[6]SchwabikˇS.Generalized ordinary dif f erential equations[M].Singapore：World Sci.,1992.

[7]Kurzweil J.Generalized ordinary dif f erential equations and continuous dependence on a parameter[J].Czechoslovak Math.J.,1957,82：418-449.

[8]Slav´ık A.Averaging dynamic equations on time scales[J].Appl.Math.,2012,388：998-1012.

[9]Federson M,Mesquita J G.Averaging for retarded functional dif f erential equations[J].Appl.Math., 2011,388：77-85.

[10]SchwabikˇS.Generalized ordinary dif f erential equations[M].Singapore：World Sci.,1991.

[11]Schmaedeke W W.Optimal control theory for nonlinear vector dif f erential equations containing measures[J].J.SIAM Control,1965,3：231-280.

[12]Das P C,Sharma R R.On optimal comtrols for measure delay-dif f erential equations[J].J.SIAM Control,1971,9：43-61.

[13]Li Baolin,Gou Haide.Bounded variation solutions for retarded functional dif f erential equations[J]. J.Math.,2015,3,567-578.

无限滞后测度泛函微分方程的平均化

李宝麟,王保弟

(西北师范大学数学与统计学院,甘肃兰州730070)

本文研究了无限滞后测度泛函微分方程的平均化.利用广义常微分方程的平均化方法,在无限滞后测度泛函微分方程可以转化为广义常微分方程的基础上,获得了这类方程的周期和非周期平均化定理,推广了一些相关的结果.

平均化方法;测度泛函微分方程;广义常微分方程;Kurzweil-Stieltjes积分

O175.12

A

0255-7797(2017)05-0987-12

∗Received date：2016-05-11Accepted date：2016-08-23

Supported by the National Natural Science Foundation of China(11061031).

Biography：Li Baolin(1963-),male,born at Tianshui,Gansu,professor,major in ordinary dif f erential equations and topological dynamical systems.

2010 MR Subject Classif i cation：26A42;34A12;34K33;39A10