气象条件影响的航段延误高维异常检测
王时敏,林 彬
(南京航空航天大学 民航学院,南京 210016)
气象条件影响的航段延误高维异常检测
王时敏,林 彬
(南京航空航天大学 民航学院,南京 210016)
海量航班延误数据中包含着少部分在恶劣天气条件下,仍有着较低延误水平的记录,这些案例为后期研究管制员在恶劣天气下的应对策略提供了学习样本.因涉及的变量较多,在分析高维空间特性的基础上,详述了高维属性在运用传统异常检测算法时的不适应性,重点阐述了一种基于谱聚类投影的异常检测算法,先将高维属性依此投影到低维空间,再运用局部离群因子作为隶属度函数进行异常检测,不仅能有效地处理高维数据的稀疏性问题,也能处理混合型的数据集,可解释性强.最后运用此算法高效地识别出了恶劣气象条件下低延误值的实例.
异常检测;高维数据;稀松性;谱聚类
天气是影响延误不可控的因素,但是在交通需求量大且气象条件恶劣的情况下,仍然有很多记录有着较低的延误值,这些案例为后期研究管制员在恶劣天气下的应对策略提供了学习样本.本实验旨在找到影响单航段延误的全局关键因素,通过在日均流量较大的机场之间建立受恶劣气象条件影响的延误网络,找出此网络中的异常点,即那些不利天气下的低延误记录,为进一步改进管制手段提供参考.
所谓异常检测,即从大规模数据中找到少量的关键异常样本.有时所谓异常正是人们真正关心的部分,为进一步探究其原因提供了切入口,本例即是如此.近些年来,异常检测算法作为一个独立分支逐渐成型,而不再只是作为聚类算法的应用之一.传统的异常挖掘主要是基于统计模型、密度分布、距离测量等.这些方法主要针对低维数值型数据集,在处理高维大规模数据集时计算效率低下,表现出种种不适应性.
维灾[1]是高维空间几何学产生的,泛指在数据分析中因属性过多而引起的所有问题.数据集要在高维空间中生成相同密度的数据点,则该数据集的大小随维数呈指数增长,若一个一维样本包n含个数据点,要在k维空间里获得同样的密度,因数据在高维空间中的稀疏性,就需要nk个数据点,也就是说即使在一个很大的范围内很可能连一个点也不包含.或者说如果体积是一定的,高维空间的物体比低维空间的物体拥有更大的表面积,导致样本密度低,往往不符合数据挖掘的要求.
在低维空间中,异常点的概念大多指与别的样本在距离或密度上差异过大,过分依赖于网格划分或是索引结构.当维度剧增时,样本之间因高维稀疏性几乎是等距离的[1],传统的基于距离的聚类方法不再适用,因为每个样本基于在距离或密度的层面都可以看作是异常,必须重新定义异常的概念并设计适当的算法.对于高维数据,一般通过以下两种方式处理:降维、子空间投影等.
传统的降维方法分为两类:特征选择和特征变换.特征选择方法依据是否会影响到后续学习算法分为过滤式和封装式两种.前者与独立于后续算法,直接采用全部训练数据的属性特征参与运算,计算速度快但与之后的学习算法结果偏差较大;后者偏差较小但计算量较大,并不适合于大数据量.特征变换不同于特征选择之处在于其输出结果不是原有的属性,而是基于某种变换原则所产生的新属性.由于变换后的属性改变了原有属性的物理特性,同时一些特征变换方法通常针对连续属性数据,再此不考虑特征变换方法.
其他主要缺陷在于:1)需先验知识才能确定相关参数,算法适应性较差;2)无法控制分类的正确率,没有给出如何通过控制错分概率达到分类效果最优化;3)可解释性差,不能直观简洁地反映异常数据产生的原因;4)能处理的数据类型单一,或者是数值型、或者离散型.本例中涉及的变量庞杂,属于高维异常检测的范畴,这些算法应用于高维分析时检测性能显著下降,可解释性更无从谈起.分析高维数据的特性,并以此设计适用于高维属性的异常检测很有现实意义.R·Agrawal[2]在其关于高维度数据的自动子空间聚类论文中给出了CLIQUE算法、包括单调性定理及其证明.Kriegel等人[3]认为,基于角度的测量在高维空间比基于距离的测量更稳定,利用余弦角度方差作为判断依据,可避免基于距离计算时出现的维灾.Aggarwal 和Yu[4]讨论了将高维属性集投影到低维子空间,在基于子空间投影的稀疏程度识别孤立点.Jiawei Han等[5]对常用的异常检测方法及其适用范围做了较为完整的总结.陈圣楠[6]在基于角度方差的高维异常检测算法基础上,结合了粗糙集理论,为属性的重要度进行排序,提出了多层次异常数据检测算法HODA;通过对数据进行网格划分来分析数据在各维度上的分布,寻找潜存着异常点的网格;最后通过对这些网格计算角度方差异常因子识别异常点.
1 研究数据及检测原理
1.1研究数据
本文所用的航班信息数据为2014年上半年旅客吞吐量位居全国前20名的机场的航班信息,每条样本包括实际起落时间、计划起落时间、航空器注册号、起飞机场、目的地机场、计划备降机场、经停次数、机型、航班类型、实际滑出时间和计划滑出时间等属性,其中航班延误时间定义为实际滑出时间与计划滑出时间的差,筛选出延误不大于15 min的样本.
本文所用的气象报文数据为2014年上半年旅客吞吐量位居中国前20位机场的METAR报文以及TAF报文,数据由自动气象站采集而来,它由传感器、数据采集处理器和显示终端组成,能自动收集和传递气象信息,主要用于观测:气压、气温、相对湿度、风向风速等,以中国民航气象报的方式发布.
1.2检测原理
将METAR报和TAF报的气象条件部分与飞行计划数据库相对应.报文以半小时为间隔发布一次,将每个发布时刻前后15 min内起飞的航班认定为受此气象条件影响.本文使用2014年上半年旅客吞吐量位居中国前20位机场的航班信息集合和与之对应METAR报文.METAR报文经处理后提取出以下几列信息:机场名称、时间、风向风速、能见度、气象信息、云层、温度/露点、修正海压、近期天气等,其中气象信息可细分为降雨、雪、雾、霾、雷暴、积冰、颠簸等.
不同的天气类型及其发生的时段导致的延误程度不同.高峰小时的天气状况会更显著的影响航班延误程度,恶劣天气的持续时间决定了机场高峰时段的需求在多大程度上能被满足,并由此决定了机场延误水平.本文将需求交通量分为机场的和航路的,将一天24 h等分成12个区间,每个区间对应两个交通运量,分别是机场离场需求交通量和机场进场需求交通量,此外还有航段需求交通量,定义为所在时段内飞经该航段的航空器架次,三者共同构成了交通运量分布.
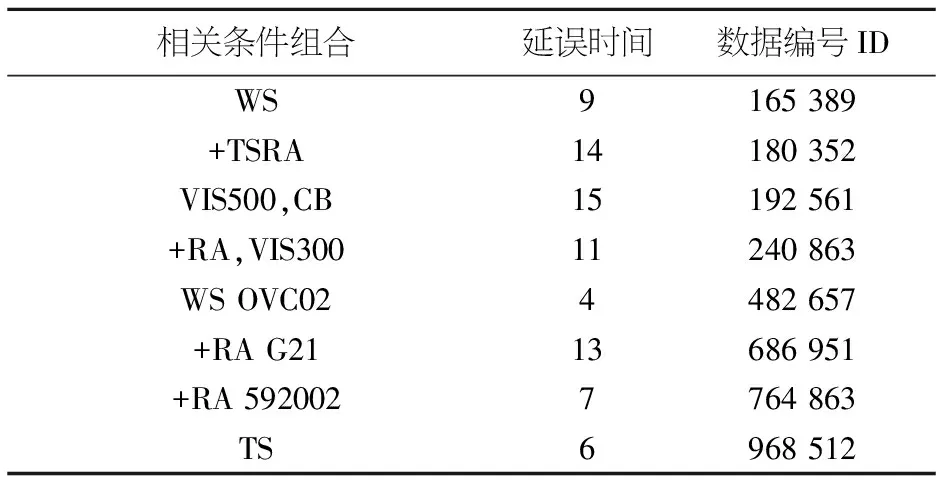
按时间段,将每一航段涉及的机场及其气象条件、交通量、航班信息连接,再将10个机场之间的所有航段两两相连,最终建成由20个气象数据、5个交通需求量数据、8个航班信息、20个机场OD对间延误时间组成的高维向量.对以上采集的样本数据经预处理后,依次为每个属性编号,并对其主要属性归类.见表1.
本文主要针对高维属性的特点,给出了一种两阶段的异常检测算法.第一阶段对数据集在各属性维上的投影聚类,分别进行初始聚类优化,依次对各属性维聚类结果计算笛卡尔交集,在计算笛卡尔交集的过程中,根据事先设定的剪枝策略对中间结果集进行剪枝,剔除掉包含数据点数低于阈值的候选集,直到所有维组合完毕,最终得到在整个维空间聚类结果;第二阶段依据全维聚类结果计算剪枝点的隶属度,隶属度函数选取局部离群因子函数(LOF),根据设定的隶属度阈值τ,对检测出的点区分噪声和异常点,并对异常点做出解释.
首先,将空间中的所有属性编号,若属性维Vi是如能见度、云高、风速、温度等的数值型属性;对属性维Vi进行单维投影聚类,如果属性维是型如雷暴、雾、风切变等类别属性,则对其概念化分类.
其次,依次对所有维度投影聚类,因为每一种属性的数据特征各异,属性按照能在任意形状的样本空间上聚类的谱分解聚类,得到类集Cn.谱聚类算法是聚类分析中一个崭新的分支,建立在谱图理论基础上,其本质是将聚类问题转化为图的最优划分问题,具收敛于全局最优解.这种算法不用对数据的全局结构作假设,非常适合于许多实际问题.通常的聚类算法等都是只适用于凸球形的样本空间,否则常常会陷入局部最优而非全局最优.
1) 定义相似度矩阵W,其中wij为标准化的样本ai和aj之间的欧几里得距离.


表1 经过处理后的每个航班数据集合字段信息
2) 由相似度矩阵计算Laplacian矩阵L
L=D-W
3) 对上述矩阵进行特征值分解,分别求得特征值和特征向量,构建特征向量空间;
4) 将原样本集的数据通过谱分析投影到由所选取的特征向量生成的新的子空间上,对新的子空间中的数据聚类得到最终的聚类结果.
再次,依次选取相邻的属性Vi和Vi+l(i=1,2,3,…,n),对其相应的类集计算笛卡尔积Ci⊗Ci+l,对得到的中间结果Mi设定阈值τ.若Mi<τ,即该分支的数量过少,被剔除.迭代计算余下的属性与保留的Mi的笛卡儿积,剪枝过程也随之迭代进行.
最后,计算每个最终组合的样本数目Qi的隶属度Pi,判断是否为异常点. 此部分相应的伪代码如表2、图1所示:
for(dimension fromV1toVn)//共n个维度
{
if(Viis numerical)
{
//将Vi进行单维数据投影聚类,生成对应的聚类,记录相应的聚类信息
for (neighbor clustersDa,DbinVidimension)
{
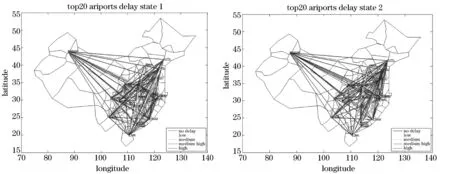
If(Da,b { 聚类合并 } } 把Vi的聚类结果保存到Mi } else if (Viis Boolean ||Viis other type){ 概念化分类,聚类结果保存到Mi } } for(M1toMn) { //在该维度计算笛卡尔积 (共有L个组合,Qi表示每个最终组合的样本数目) for(Q1toQL) { If(Qi<阈值1,) { 计算Qi的隶属度Pi If (Pi<阈值2) { 确定为异常点 } else { 计算与最接近的聚类的差异程度 } } } 因同样气象条件及需求分布条件下,不同航班记录的延误分布规律差异很大,关于隶属度Pi,本文采用一种针对密度分散情况迥异集合的异常点识别方式,即局部异常因子算法-Local Outlier Factor(LOF)来衡量.相关算法如下: 1)d(a,o)为样本a和样本o之间的距离; 2)对于样本a的第k距离dk(a)定义为距离样本a第k远的样本(不含样本a)的距离. 3)样本a的第k距离邻域Nk(a),即以样本a为圆心,以dk(a)为半径所涵盖范围内包含的全部样本,也包括其边界.显然,这一范围内所包含的样本个数不少于k. 4) 样本o到样本a的第k可达距离定义为:reach-distk(a,o)=max{dk(a),d(a,o)} 可以理解为至少是样本o的第k距离,或是样本o与a样本间的欧几里得距离.也就是说,样本o到离其最近k的个样本的可达距离都为d(o). 5) 样本的局部可达密度表示为: 即样本a的Nk(a)到样本a的平均可达距离取倒数.如果样本a不是异常点,那么其可达距离取dk(o)的概率越大,此时分母较小,局部可达密度越大;反之,如果样本a是潜在异常点,那么其可达距离取d(a,o)的概率越大,此时分母较大,局部可达密度较小. 6)样本a的局部离群因子表示为: 表示样本a的邻域点Nk(a)的局部可达密度与样本a的局部可达密度之比的平均数.若比值越接近1,该样本点越可能和邻域同属一簇;若比值越远小于1,说明此样本比其领域内的其他样本平均密度大;若比值越远大于1,说明此样本比其领域内的其他样本平均密度小,也就潜在的异常点. 根据上述算法,在2012年上半年旅客吞吐量位居全国前20名的机场的航班信息中,当τ≤3时共检测出的312条恶劣天气下的低延误样本,再依据数据编号在数据库中识别出对应记录.部分异常样本如表2,图1所示: 表2 检测出的异常样本部分示例汇总 剔除掉异常点之后,可观测到全国主要机场OD对间的宏观延误水平,为了便于对比,本文将延误分为五个等级,依次为小于15 min;大于15 min小于30 min;大于30 min小于45 min;大于45 min小于60 min;60 min以上. 图1 剔除异常点前后的延误网络对比 海量航班延误数据中包含着少部分在恶劣天气条件下,仍有着较低延误水平的记录,这些案例为后期研究管制员在恶劣天气下的应对策略提供了学习样本.因涉及的变量较多,本文在分析高维空间特性的基础上,详述了高维属性在运用传统异常检测算法时的不适应性,重点阐述了一种基于谱聚类投影的异常检测算法,先将高维属性依此投影到低维空间,再运用局部离群因子作为隶属度函数进行异常检测,不仅能有效地处理高维数据的稀疏性问题,也能处理混合型的数据集,可解释性强.最后运用此算法高效地识别出了恶劣气象条件下低延误值的实例. [1] BELLMAN R. Adaptive control processes: a guided tour [M]. Princeton: Princeton University Press, 1961. [2] AGRAWAL R, GEHRKE J, GUNOPULOS D,etal. Automatic subspace clustering of high dimensional data for data mining applications [P]. United States Patent: 6003029, 1999-12-14. [3] KRIEGEL H P, HUBERT M S, ZIMEK A. Angle-based outlier detection in high-dimensional data[C]// Las Vegas: 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2008. 444-452. [4] AGGARWAL C C, YU P. Outlier detection for high dimensional data [J]. ACM SIGMOD Record, 2001, 30(2): 37-46. [5] 丁 洁, 王 磊, 沈荻帆, 等. A一种大数据异常检测系统的研究与实现[J]. 海南大学学报:自然科学版, 2015, 33(1): 24-27+33. [6] 陈圣楠, 钱红燕, 李 伟. 基于角度方差的多层次高维数据异常检测算法[J]. 计算机应用研究, 2016, 33(11): 3383-3386. Researchonoutlierdetectionforhighdimensionalweather-impactedflightsegmentdelay WANG Shi-min, LIN Bin (School of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China) Massive delays data contains a few valuable information of low delay level in bad weather conditions, which provides ATC with learning samples for the later research about the best solution in severe weather atmosphere. Due to vast variable involved, based on the characteristics of high-dimensional space, it was analyzed why traditional anomaly detection algorithm was not suitable for high dimensional attribute. And this paper explored an anomaly detection algorithm based on spectral cluster and projection, which firstly projects the high-dimensional attributes to low dimensional space, and uses local outlier factor as membership functions in anomaly detection. The result could not only effectively handle data sparseness of high-dimensional data, also could deal with both numeric and Boolean type attribute, and explain the abnormal. An application example of low delay level of flight segment affected by bad weather is given to validate the feasibility and effectiveness of the algorithm. outlier detection; high dimensional data; sparseness; spectral clustering 2016-11-14. 王时敏(1989-),女,硕士,研究方向:空域规划与管理. V355 :A 1672-0946(2017)04-0502-05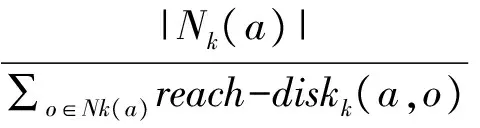
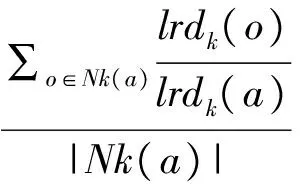

2 验证结果
3 结 语

