最佳估算方法在核临界安全分析的应用研究

陈 添，霍小东，杨海峰，易 璇

(中国核电工程有限公司，北京100840)

最佳估算方法在核临界安全分析的应用研究

陈 添，霍小东，杨海峰，易 璇

(中国核电工程有限公司，北京100840)

最佳估算方法可以同时对多个参数按概率分布进行抽样，从而模拟系统真实的物理状况，计算结果的容忍区间及置信水平与抽样数目有关。本文将最佳估算方法应用于压水堆核电站乏燃料贮存格架和燃料运输容器的临界安全分析，采用非参数抽样统计方法，多参数同时抽样，并对各抽样参数的敏感度进行分析。抽样计算的结果统计分析表明，最佳估算方法更接近真实值，证明原逐参数单独进行敏感性分析方法的保守性并得到相应的保守裕量；对于特定研究对象参数的敏感性排序是稳定的，主要取决于参数自身的敏感性，参数的范围及分布的影响较小，应在相关设备的设计与制造中重点关注敏感度高的参数。

最佳估算方法；临界安全分析；非参数抽样统计方法；参数敏感性分析；乏燃料贮存格架；燃料运输容器

最佳估算方法，就是尽可能模拟物理现象真实情况的方法。近数十年，多个研究机构对最佳估算分析方法进行了大量的研究和开发工作[1]。最佳估算方法广泛应用于核安全分析以得到更实际的安全限值[2]，如在AP1000大破口失水事故分析中的应用。核临界安全是核科技工业的特殊安全问题，在核燃料的加工、使用、贮存和运输等过程中紧密伴随着临界问题。在临界安全计算中，通常采用保守的参数取值，这种做法一方面无法证明其保守性，另一方面也无法知道其保守程度。在复杂系统多参数同时变化的情况下，保守判断更加困难。目前，最佳估算方法在临界安全分析领域中还未有广泛的应用。在临界安全分析中应用最佳估算方法，可以部分解决保守性证明及保守裕量问题。

本文采用的抽样统计方法是最佳估算理论中的非参数抽样统计方法。通过比较最佳估算和保守方法的结果可以计算出安全裕量。将多次抽样临界计算的结果进行线性回归分析，得到参数敏感性的排序，以确定对结果影响较大的几个参数。在临界安全分析中应用最佳估算方法可以模拟系统真实的物理状况，分析复杂系统中多参数同时变化的影响，验证传统保守方法的正确性并能够计算保守程度，是对保守方法的补充和优化，同时根据敏感度较大的参数提出一些工程上的建议。

1 最佳估算方法

最佳估算加不确定度评估方法是核电厂安全分析的一种方法，基于输入参数不确定度评估目标参数的不确定度，包括确定重要输入参数与分布、抽样、结果统计分析等流程。其中最佳估算分析中的抽样统计方法分为两种，即参数抽样统计和非参数抽样统计。这两种方法在抽样次数和结果处理上有较大的区别。

1.1 参数抽样统计方法

参数抽样统计方法[3]根据重要输入参数的概率密度分布对每个参数分别进行抽样，将抽样的参数进行组合，作为模型分析的输入，然后得到目标参数的分布，通过分布检验、计算均值和方差后经过统计处理得到置信限值。根据概率密度分布进行抽样可以采用简单随机抽样、分层抽样以及拉丁超立方抽样等抽样技术。参数抽样统计方法避免了保守方法中参数只取端点值、中心值等固定取值的缺陷，考虑得更全面。参数抽样统计方法为了获得准确的目标参数分布，当模型复杂、参数很多时，产生大量的参数组合，计算量很大，优点是大量计算下的目标参数的估计可信度较高，并且能够得到目标参数的近似分布。

1.2 非参数抽样统计方法

非参数抽样统计方法[3-6]解决的问题是得到在一定置信水平下得到的抽样总体在一定概率水平的上边界限值(或双边界限值)。非参数抽样统计方法对所有确定的重要输入参数同时抽样，抽样次数和输入参数的多少无关，只与输出结果的容忍区间和置信水平有关,适合于复杂模型，使用较少的抽样数量达到一定的概率水平和置信度，效率较高。满足特定容忍区间的最小抽样数目由Wilks公式确定，其表达式如下：

单侧容忍区间：

β=1-αN

(1)

双侧容忍区间：

β=1-aN-N(1-α)αN-1

(2)

式中：α为概率或容忍限值；β为置信水平；N为抽样计算数目。这里的α可以理解为抽样计算结果的最大值对应的累积概率。α定义为：

(3)

式中：f(x)是连续变量x的概率密度函数，xup是x的上容忍限值。

对于单侧容忍区间公式，当α=95%，β=95%时，N=59，即抽样计算59次得到抽样总体在95%概率水平的上边界值的置信度为95%(抽样59次计算结果的最大值大于容忍限0.95对应的值的概率为95%)，即“95/95准则”。非参数抽样统计方法的优点是用较少的抽样次数得到目标参数的限值，缺点是较少的抽样计算不能得到目标参数的近似分布。值得注意的是，在核临界安全分析中应用最佳估算方法计算的“95/95”限值是在一定概率和置信度下得到的，在实际状况中是有可能达到该限值的，所以不能作为临界安全的保守限值，但是可以作为对实际状况可能达到的最大值的估计和判断临界分析保守性的一种参考。

2 最佳估算方法在核临界安全分析中的应用

2.1 多参数敏感性分析方法

本文编写了参数抽样程序，采用非参数抽样统计方法，可以通过输入参数说明文件和临界计算模板文件得到指定数目的临界计算输入文件，即可使用临界程序MONK进行计算，其中参数说明文件包括参与抽样参数的数目、分布以及分布范围数据，临界计算模板文件为MONK程序输入文件，通过最佳估算参数抽样程序进行参数抽样并修改相关参数形成完整输入文件。整个最佳估算分析的流程如图1所示。

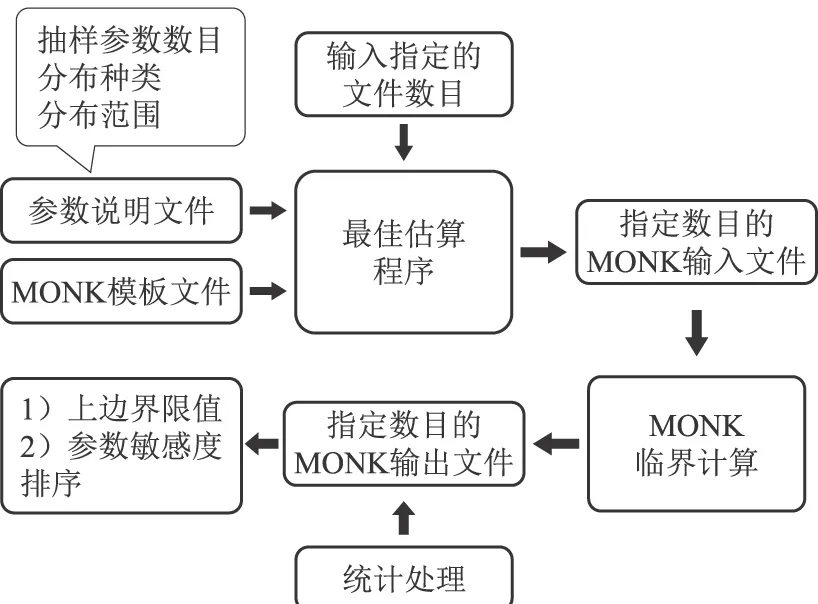
图1 最佳估算分析流程Fig.1 Best Estimate analysis procedure

对计算得到的多个文件进行数据处理，给出有效增殖系数keff随每个参数的变化图，由于是多个参数同时抽样对keff产生影响，所以keff随单个参数的变化图为散点图。keff随敏感度大的参数的变化有明显的线性趋势；keff随敏感度小的参数的变化由于被敏感度大的参数影响淹没，散点分布无规律。考虑参数的变化范围为制造公差或接近实际情况，可以认为是微扰，keff随参数的变化近似为线性变化。采用线性回归拟合的相关系数平方R2来量化keff随参数变化的线性程度，进而量化对该参数的敏感度。线性拟合相关系数平方R2的表达式如下：

(4)

式中：k为增殖系数，x为参数。R2代表k与x的线性相关度，越接近1代表线性相关性越大，越接近0代表线性相关性越弱。图2给出了乏燃料贮存格架系统有效增殖系数keff随一个敏感度较大和一个敏感度较小的参数变化的散点图以及线性回归拟合。

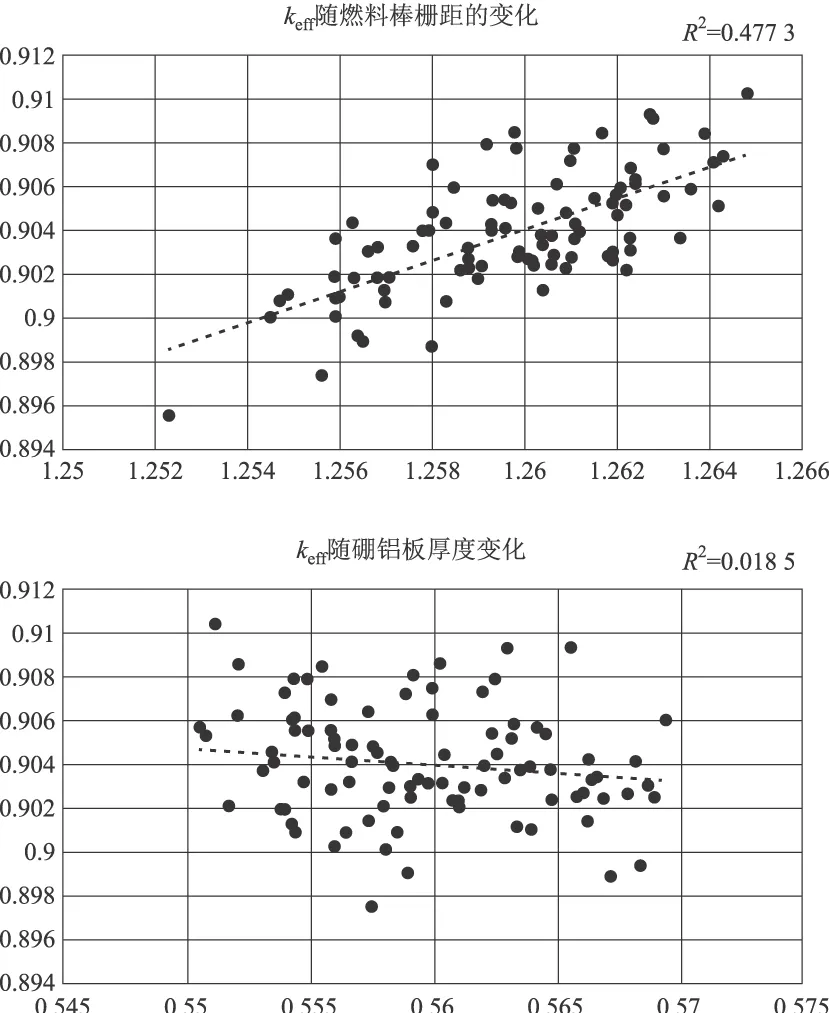
图2 乏燃料贮存格架有效增殖系数随两个参数变化图Fig.2 Scatter diagram of keff changing with the parameter in spent fuel storage rack model

从图2中可以看出keff在多参数同时抽样变化的情况下仍随燃料棒栅距的增加有明显的增大趋势，而keff随中子吸收硼铝板厚度的变化没有明显的变化趋势。通过线性回归拟合得到的相关系数平方R2可以量化其线性程度，该线性程度可以代表keff对于该参数的敏感度。通过比较各参数的线性拟合相关系数平方R2的大小可以对参数的敏感度进行排序。

相关系数R2与很多因素相关。从参数的角度来说，R2和参数自身的敏感性、分布种类、变化范围都有关系，若分布为均匀分布，则拟合的线性程度更高；若变化范围选得越大，则在固定抽样次数下keff变化的范围也越大，R2也越大。从随机抽样的角度来说，不同的多次抽样的线性回归拟合将得到不同的相关系数，所以也需要足够多抽样次数排除偶然性，保持参数敏感度排序的稳定。表1显示了运输容器模型一种工况下参数敏感度排序随抽样次数的变化，抽样次数以单侧“95/95准则”的最小抽样次数59次为基准进行倍数的变化。

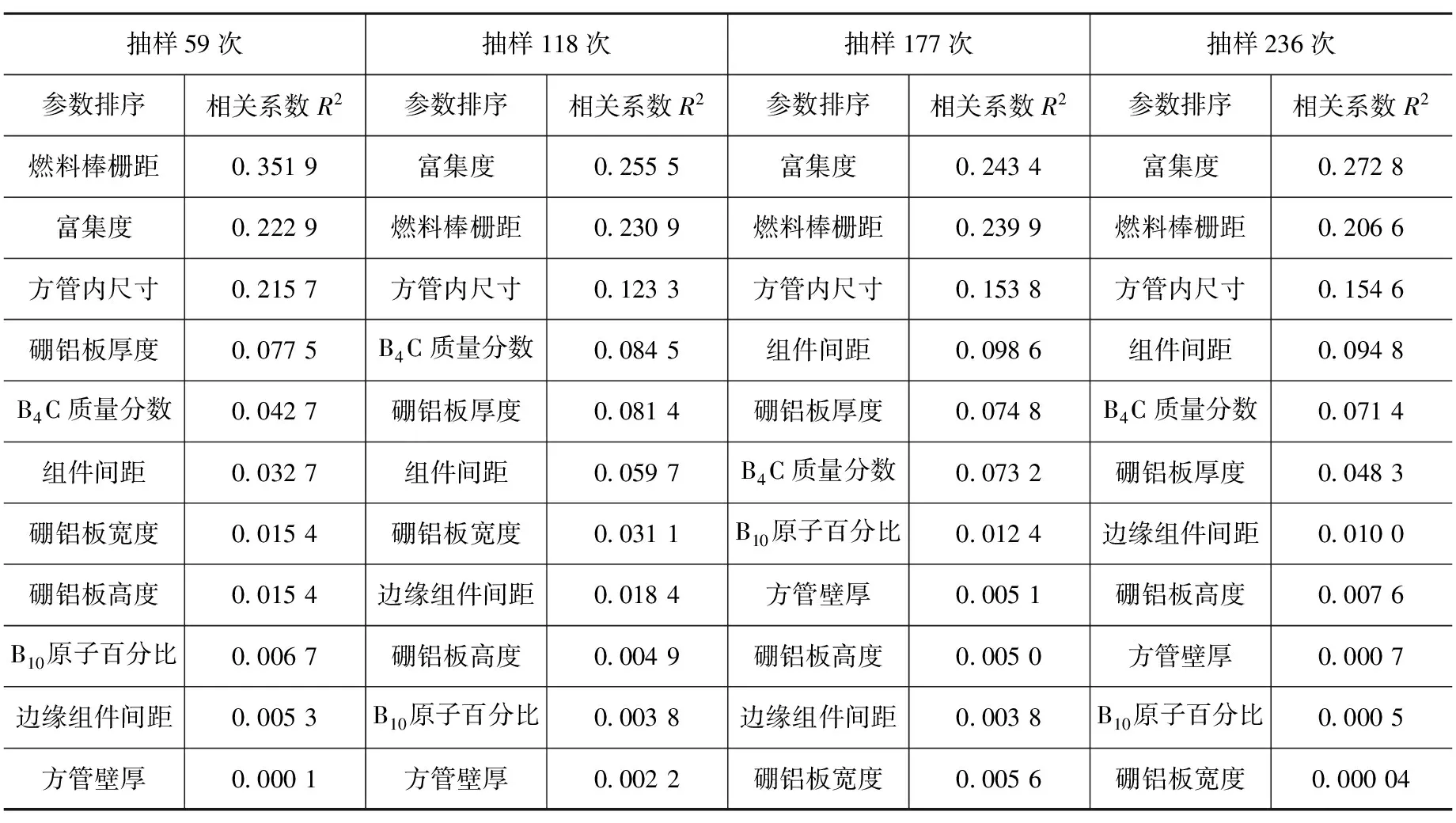
表 1 参数敏感度排序与抽样次数的关系

由表1可以看出，随着抽样次数的增多，相关系数R2较大的几个参数的排序趋于稳定，说明这种方法是稳定的。由于存在敏感度较大参数的影响，敏感度较小的参数的排序是不稳定的，所以一般取R2大于0.1参数的排序。若要比较剩余敏感度较小的参数，只要固定敏感度较大的参数，进行同样的计算和分析即可。权衡计算耗时和排序稳定性，在后续的参数敏感度排序分析中采用118次抽样。

相比于保守方法中的单参数敏感性分析，最佳估算方法中的多参数敏感性分析的计算代价比较大，但是其优势在于同时考虑了所有确定的参数对结果keff的影响，分析了keff随每个参数在其他不同敏感度参数影响下的变化情况，尤其是在参与抽样的输入参数之间还有相互关系以及某些参数组合对结果keff存在联合影响的特殊情况，这是保守方法单参数敏感性分析所考虑不到的地方。

2.2 乏燃料贮存格架模型的最佳估算分析

2.2.1 最佳估算方法与保守方法的比较

本文采用的乏燃料贮存格架模型[7]如图3所示，其中的组件为初始富集度5.0%、128根IFBA棒、平均燃耗为42.6 GWd/t(U)的乏燃料组件。中子吸收板为硼铝板，主要成分是B4C 和铝。格架内充满水，边界条件为周期边界条件。

图3 乏燃料贮存格架截面图Fig.3 Intersecting surface diagram of spent fuel storage rack

根据国标GB 15146.2[8]以及借鉴燃料贮存格架的临界安全保守分析[9]的方法，可以求出保守方法下的有效增殖系数的最大值，即为保守考虑下的系统keff限值。共9个参数进行单参数不确定度计算，如表2所示。

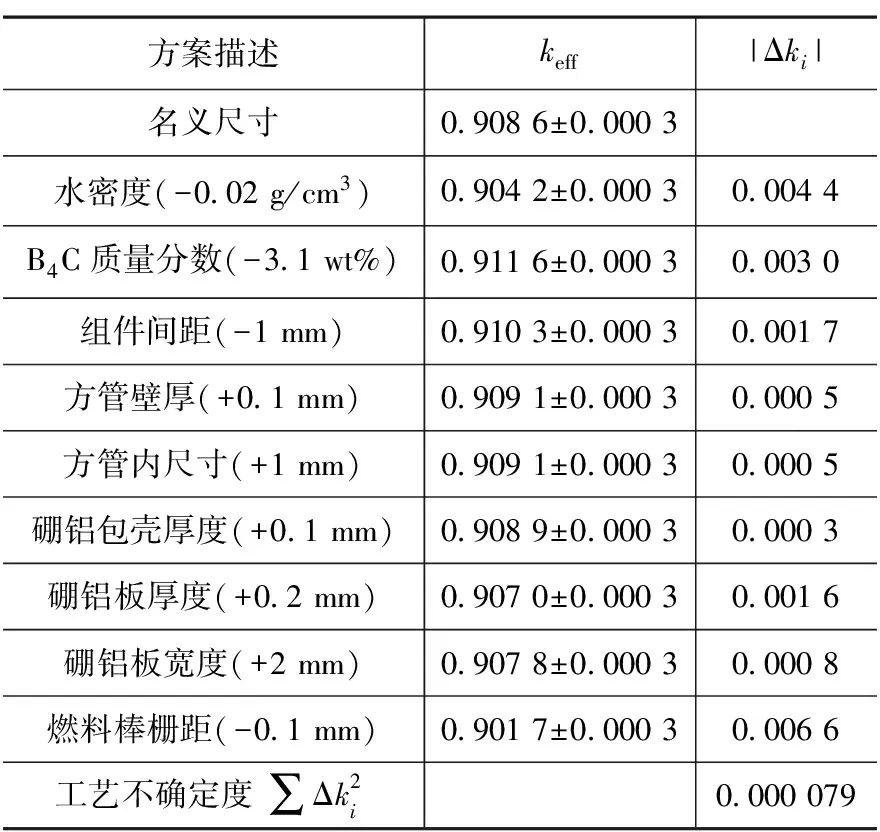
表 2 参数的不确定度计算

在不考虑计算偏差和计算不确定度的情况下，保守方法keff计算的限值为:

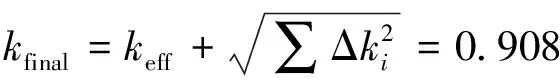
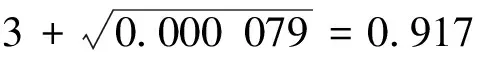
另一方面采用最佳估算方法，对结构中间的9个组件的位置参数在几何允许的范围内进行均匀分布随机抽样，即有18个参数，除此之外，还对除了组件间距以外的8个参数进行随机抽样，如表3所示。

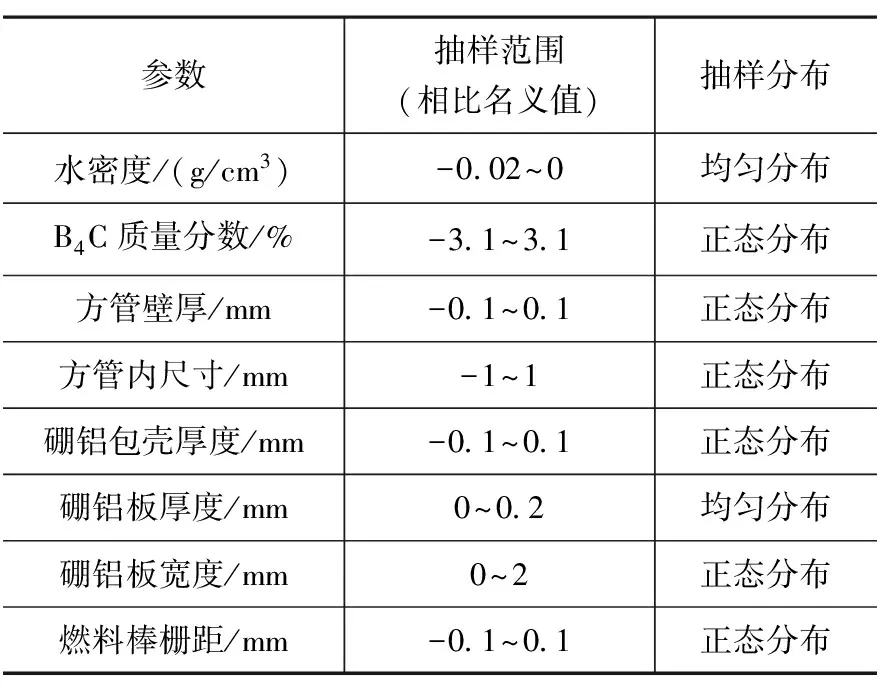
表 3 参与抽样的参数信息

对共26个参数同时进行59次抽样计算，keff的最大值为：0.9111+0.0003。最佳估算方法得到的抽样总体在95%概率水平上边界限值0.9114的置信度为95%。保守方法结果和最佳估算方法结果相比的裕度为：

kfinal-kmax=0.917 8-(0.911 1+

0.000 3)=0.006 4

该结果说明最佳估算方法是更接近真实情况的计算方法，也验证了保守方法的保守性，计算了保守程度。

2.2.2 多参数敏感性分析

采用2.1节的多参数敏感性分析方法，进行118次抽样计算，对结果进行线性回归分析，比较排序各个参数的线性拟合相关系数平方R2，以此为依据排序系统增殖系数对各参数的敏感度，结果如表4所示。

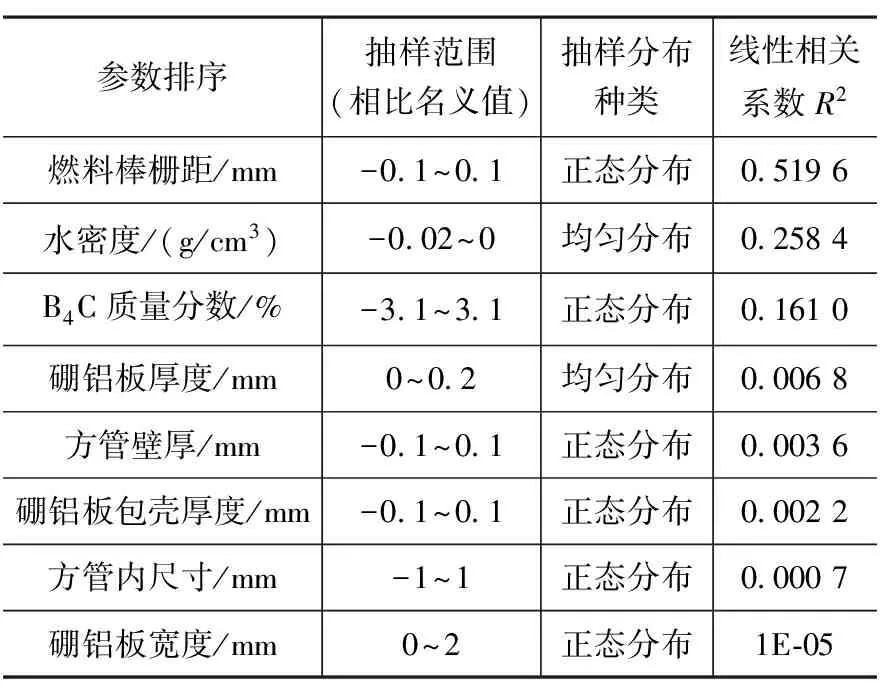
表 4 乏燃料贮存格架临界分析中的参数敏感度排序

由表4可以看出，在这些参数特定的抽样范围和抽样分布以及乏燃料贮存格架系统下，最敏感的3个参数是燃料棒栅距、水密度和中子吸收板中的B4C质量分数，其余参数的敏感性较小，对keff的影响被淹没。因此在乏燃料贮存格架系统需要注意这三个敏感的参数，防止燃料组件中燃料棒松动栅距变大引起的keff增加，水密度有较大的敏感度以及正向相关性，这也验证了工程上保守取水密度最大值的正确性。

将最佳估算线性回归分析得到的参数敏感度排序(线性相关系数平方R2的排序)与保守方法单参数变化得到的敏感度排序(单参数变化|Δk|的排序)进行比较，结果如表5所示。

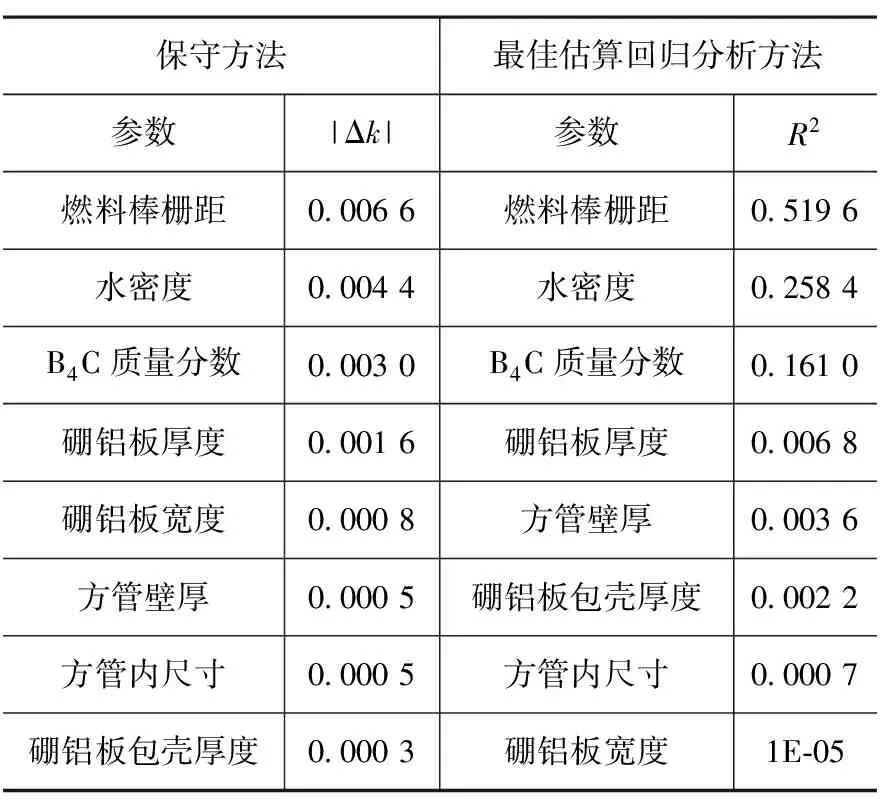
表 5 最佳估算回归分析得到的参数敏感度排序与保守方法得到敏感度排序的比较

由表5可以看出最佳估算回归分析得到的敏感度排序在R2较大的几个参数在抽样次数较多的情况下与保守方法得到的基本一致，这也验证了最佳估算回归分析得到的敏感度排序的正确性，也可以验证取R2大于0.1的参数排序是正确的、保守的。而R2较小的参数影响被淹没，其排序没有意义。

2.2.3 改变工况后的参数敏感度排序

若考虑乏燃料贮存格架失水的工况，并且修改部分参数的抽样分布和抽样范围(在表6中加粗显示)，对包括组件间距在内的8个参数(由于为失水工况，无水密度参数)进行抽样118次并进行临界计算，则参数的敏感度排序则会相应发生变化，结果如表6所示。

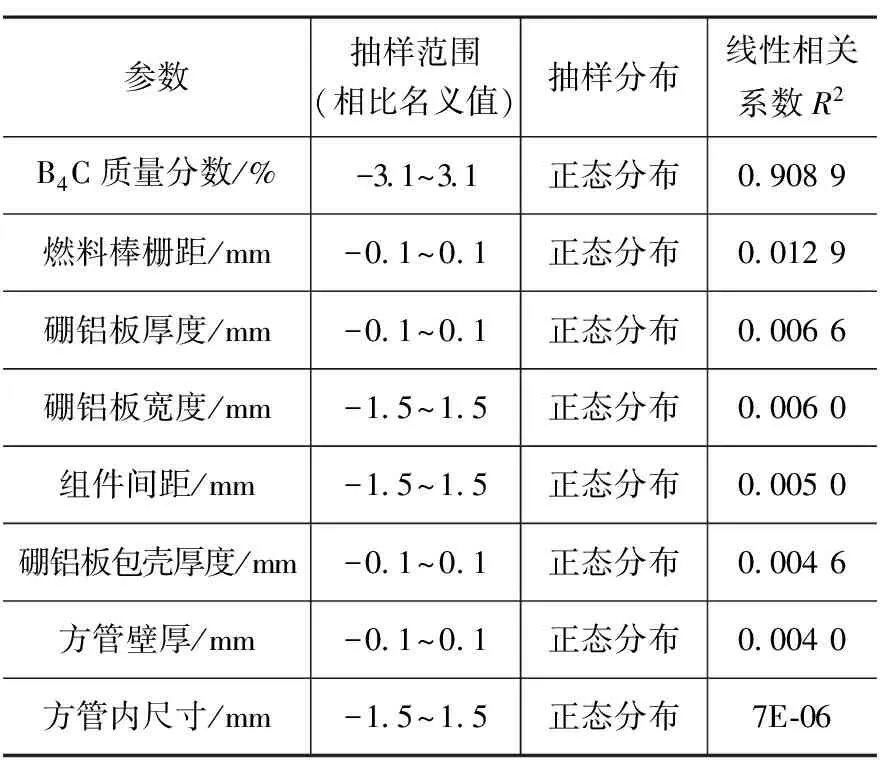
表6 乏燃料贮存格架失水事故下参数敏感度排序

由表6可以看出，在失水工况下，最敏感的参数是B4C质量分数，其他参数的线性相关系数平方R2小于0.1，这些参数的影响被淹没。相比于正常工况，燃料棒栅距这一敏感的参数在失去慢化剂的情况下变得不敏感。另外在改变部分不敏感参数的抽样分布和抽样范围时，这些参数的线性相关系数平方R2仍然较小，说明影响R2的主要因素是参数自身的敏感性，抽样分布和抽样范围的影响较小。

2.3 燃料运输容器模型的最佳估算分析

2.3.1 最佳估算方法与保守方法的比较

本文采用的燃料运输容器模型[10]如图4所示，由吊篮、γ屏蔽层、中子屏蔽层、内外筒体、底板和容器盖等部分组成。容器内有21个组件，组件外有中子吸收物硼铝板，组件间有传热片和支撑片。采用5%富集度的新燃料组件进行分析，组件间隙为真空，容器外为真空，自由边界条件。

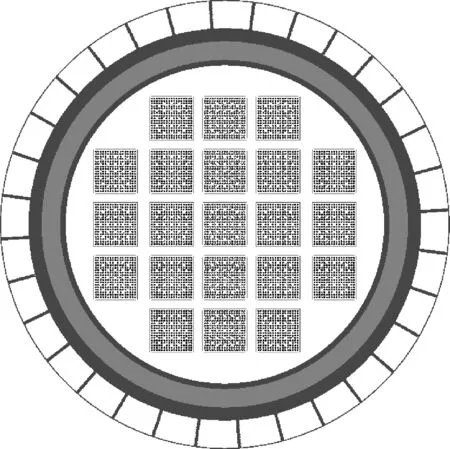
图4 燃料运输容器截面图Fig.4 Intersecting surface diagram of fuel transport package

采用同样的保守方法计算运输容器系统keff的最大值，共11个参数进行单参数不确定度计算，如表7所示。

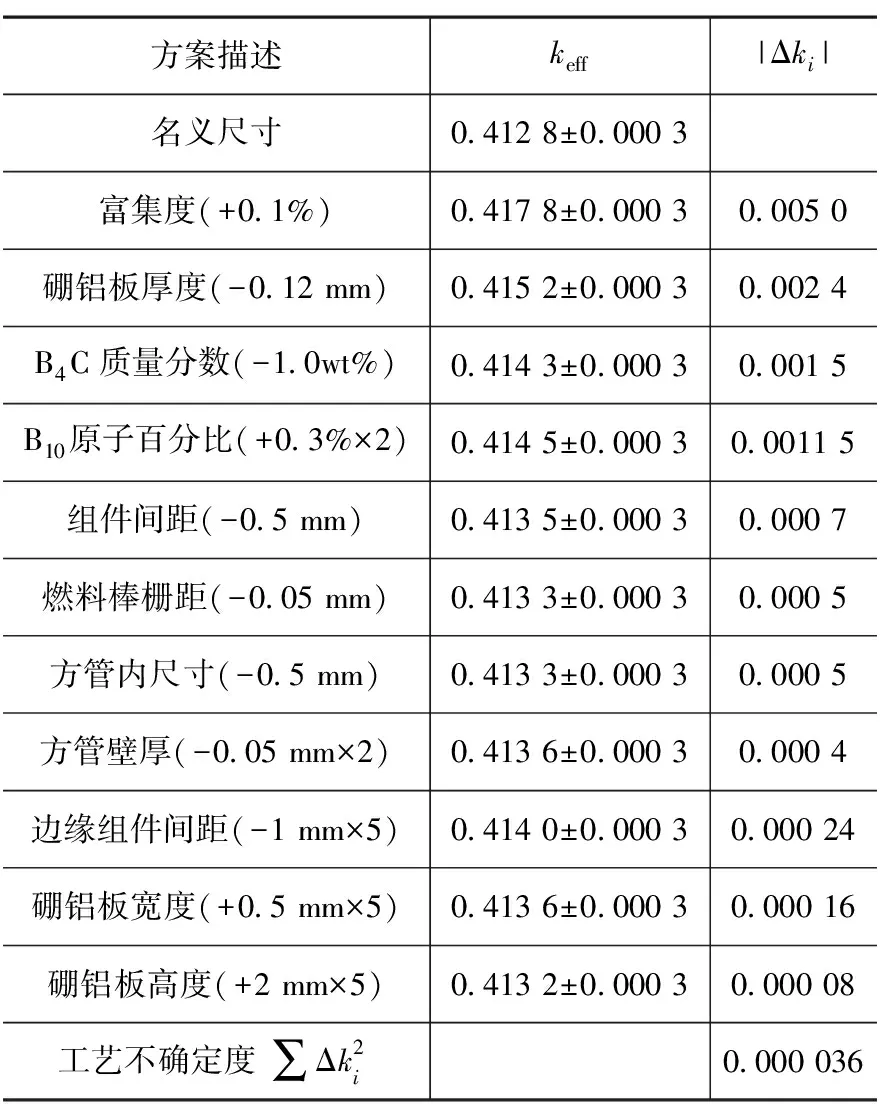
表7 参数的不确定度计算

在不考虑计算偏差和计算不确定度的情况下，keff计算的限值为:

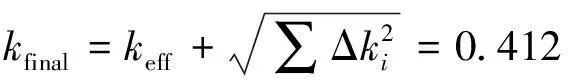
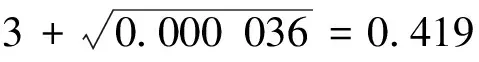
另一方面采用最佳估算方法，对同样的11个参数进行随机抽样，如表8所示。

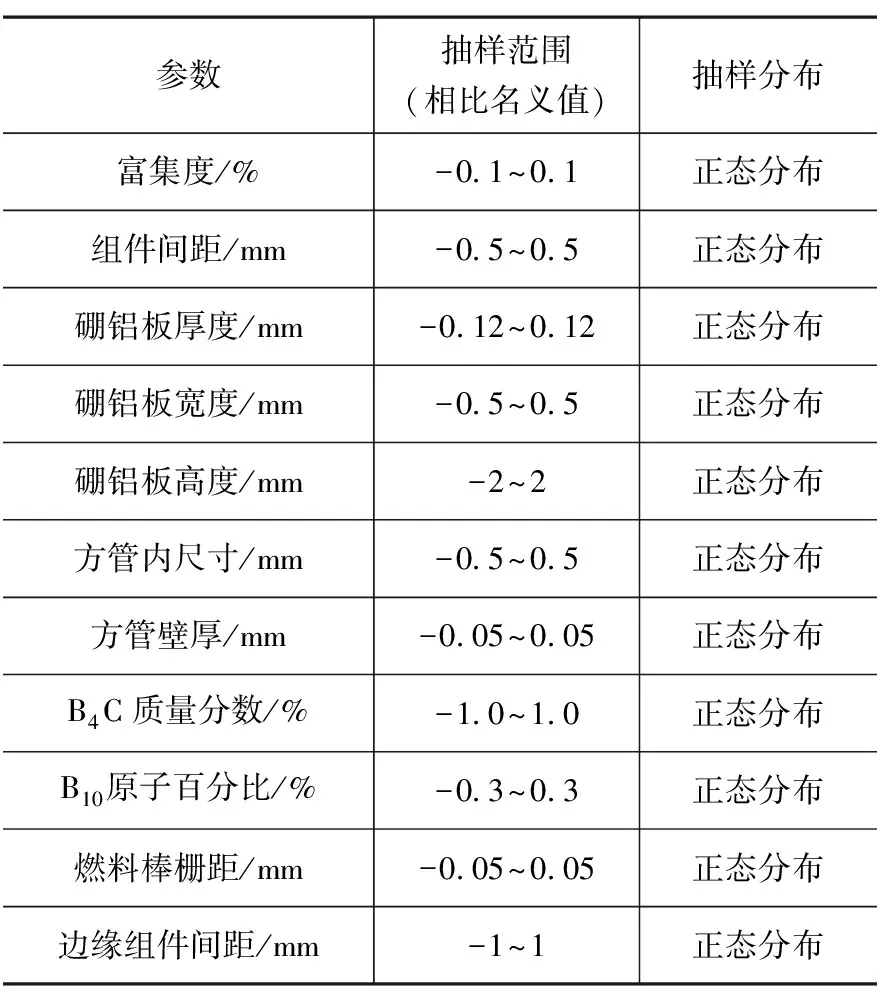
表8 参与抽样的参数信息

对11个参数同时抽样59次，keff的最大值为：0.4160+0.0003。最佳估算方法得到的抽样总体在95%概率水平上边界限值0.4163的置信度为95%。保守方法结果和最佳估算方法结果相比的裕度为：

kfinal-kmax=0.419 1-(0.416 0+

0.000 3)=0.002 8

该结果同样说明最佳估算方法是更接近真实情况的计算方法，也验证了保守方法的保守性，计算了保守程度。这里相比于乏燃料贮存格架计算的裕度要小，原因是参与抽样的参数的敏感度较小，由于系统中没有水，少了水密度这个敏感的参数，同时燃料棒栅距在缺少慢化剂的情况下也变得不敏感，导致保守方法计算的keff较小。

2.3.2 多参数敏感性分析

采用2.1节的多参数敏感性分析方法，进行118次抽样计算，对结果进行线性回归分析，比较排序各个参数的线性拟合相关系数平方R2，以此为依据排序系统keff对各参数的敏感度，结果如表9所示。

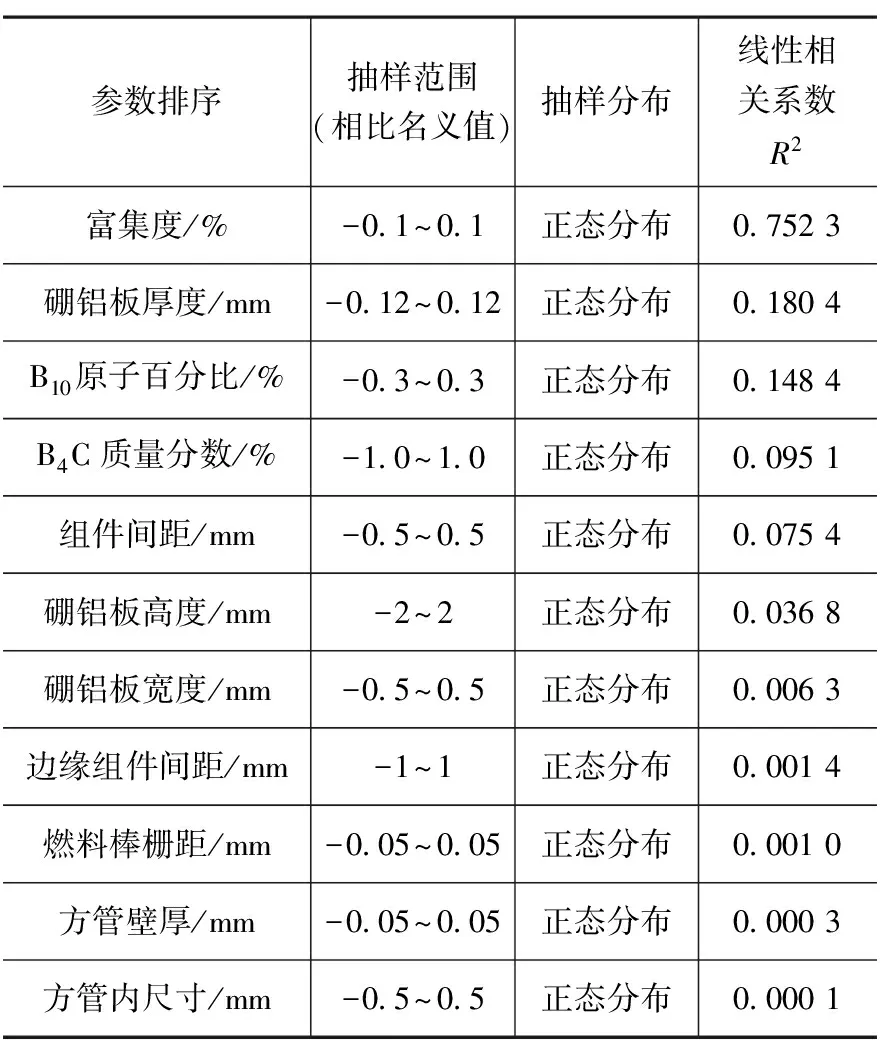
表9 燃料运输容器临界分析中的参数敏感度排序

如表9所示，最敏感的三个参数为新燃料的富集度、硼铝板厚度和B10原子百分比，这三个参数皆为燃料和中子吸收板制造过程中涉及的参数，制造的工艺水平对运输容器系统的影响较大，在工程设计和制造过程中要注意和控制这三个参数的变化范围。

通过和表7的保守方法参数敏感度分析的比较可以发现，R2较大的参数排序和单参数变化|Δk|的排序基本一致，其中对于B4C质量分数和B10原子百分比的排序不同，由于B4C质量分数和B10原子百分比的敏感度(|Δk|)比较接近，在有限的118次参数抽样计算的偶然性和随机性以及更敏感参数的影响下这两个参数R2的排序有可能不够准确。

2.3.3 改变工况后的参数敏感度排序

若考虑运输容器内进水的严重事故，则参数的敏感度排序发生较大变化，重新建模并抽样计算118次，结果如表10所示。

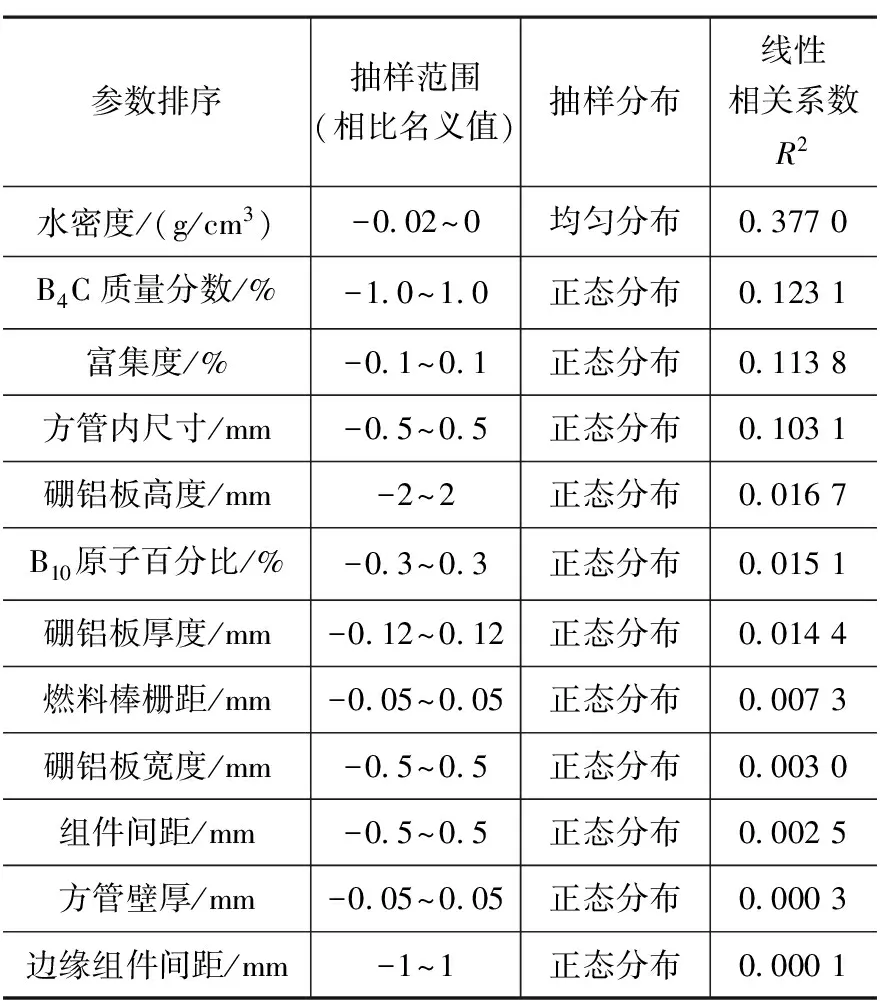
表10 燃料运输容器进水事故下的参数敏感度排序

相比于正常情况，进水事故下最敏感的四个参数是水密度、中子吸收板中B4C质量分数、新燃料富集度和方管内尺寸，其中方管内尺寸参数代表燃料组件与硼铝板的距离，进水事故工况下水密度为最敏感的参数。这也说明在不同的工况以及不同的参数抽样范围和分布下，参数的敏感度排序会发生变化，对于不同工况要做具体分析。

3 结论

(1) 本文采用最佳估算方法对乏燃料贮存格架和燃料运输容器进行了临界分析，通过59次抽样计算了抽样总体在95%概率水平的置信度为95%的上边界限值，与保守方法的计算结果进行比较，验证了保守方法的保守性，计算了保守程度，也说明了最佳估算方法更接近真实值。

(2) 对多次抽样计算的结果统计分析，通过有效增殖系数keff对参数散点图的线性回归拟合，比较各参数的线性相关系数平方R2，得到了不同模型下的参数敏感度排序，分析了复杂系统多参数同时变化的影响。线性相关系数平方R2主要取决于参数自身的敏感性，参数的抽样范围和抽样分布的影响较小。对于一个特定的系统、工况、参数选择及范围，参数的敏感度排序是稳定的。当这些条件改变时，参数的敏感度排序可能会相应发生变化。

(3) 乏燃料贮存格架模型中燃料棒栅距和水密度这两个参数比较敏感，在失水工况下B4C 质量分数是最敏感的参数；燃料运输容器模型中新燃料的富集度和硼铝板厚度的参数比较敏感，在进水事故工况下水密度和B4C质量分数则变成比较敏感的参数。在工程设计和制造中需要对这些参数进行重点关注和控制。

(4) 最佳估算方法在临界安全分析中进一步释放了安全裕量，多次抽样计算的最大值和最小值的参数组合情况以及各种工况下的参数敏感度排序对于核临界安全设计和控制有一定的指导意义，需要进一步的研究和分析。

[1] 陈炼, 房芳芳, 邓程程, 等. 核电站最佳估算安全分析中的不确定度评估方法分析[J]. 原子能科学技术, 2015, 49(7):1237-1242.

[2] 林诚格, 刘志弢, 赵瑞昌. 压水堆失水事故最佳估算方法研究[J]. 核安全, 2010, 1.

[3] 陈炼, 胡啸, 邓程程, 黄挺, 等. 最佳估算方法中不确定度评估关键问题分析[J]. 原子能科学技术, 2016, 50(5):851-858.

[4] 冉旭, 吴丹, 陈炳德, 等. 最佳估算加不确定性分析方法及其应用研究[J]. 核动力工程, 2013, 34(3):120-123.

[5] Wilks S S. Determination of Sample Sizes for Setting Tolerance Limits[J]. Ann Math Stat, 1941, 12: 91-6.

[6] Connolly A, Hong I S. Generalized Tolerance Limit Evaluation Method to Determine Statistically Meaningful Minimum Code Simulations[C]. Proceedings of the 16th International Conference on Nuclear Engineering.

[7] 杨海峰, 霍小东, 易璇, 等. 高密度乏燃料贮存格架临界安全设计[J]. 核动力工程, 2014, 12(S2):167-169.

[8] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB 15146. 2-2008 反应堆外易裂变材料的核临界安全：第2部分：易裂变材料操作、加工、处理的基本技术规则和次临界限值[S]. 北京： 中国标准出版社, 2009.

[9] 徐鹏. 燃料贮存格架的临界安全分析研究[J]. 核科学与工程, 2010, 30(S):187-195.

[10] 易璇, 霍小东. 运输容器临界安全评价要点剖析[J]. 原子能科学技术, 2013, 47(S): 309-311.

StudyonBestEstimateMethodAppliedtoNuclearCriticalitySafetyAnalysis

CHENTian，HUOXiao-dong，YANGHai-feng，YIXuan

(China Nuclear Power Engineering Co., Ltd., Beijing 100840, China)

In Best Estimate method, multiple parameters are randomly sampled at the same time according to their probability distribution. Best Estimate method aims at simulating true condition and the number of code runs is related to the tolerance percentile and confidence level. Best Estimate method is applied to the criticality analysis of spent fuel rack and fuel transport package, using nonparametric sampling approach which means that multiple parameters are sampled at the same time. The sorted sequence of parameter sensitivity is got from parameter sensitivity analysis. The statistical analysis of calculation results demonstrates that the result of Best Estimate method is closer to true-value and the method of analyzing every single parameter sensitivity is conservative. The sequence of parameter sensitivity is stable when analyzing specific condition, which mostly depends on parameter’s own sensitivity. The range and distribution of parameter have little effect on the sequence. The sensitive parameters should be paid close attention to in the design and manufacturing process of relevant equipment.

Best Estimate method；criticality safety analysis；nonparametric sampling approach；parameter sensitivity analysis；spent fuel rack；fuel transport package

2017-03-11

陈 添(1992—)，男，江苏人，助理工程师，硕士，现从事核临界安全分析相关工作

TL36

：A

：0258-0918(2017)04-0619-09