《利用“辅助圆”巧解一类动态平衡问题》一文引发的思考

蒋金团++牛云景

摘 要：对《利用“辅助圆”巧解一类动态平衡问题》一文中的解题方法进行了点评，并给出新的解法与之对比。

关键词：动态平衡；拉密定理；辅助圆

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2017）8-0036-3

《物理教学探讨》2016年第12期刊登了一篇名为《利用“辅助圆”巧解一类动态平衡问题》的文章（以下简称文献1）[1]，该文主要介绍了辅助圆在三力动态平衡问题中的应用。笔者仔细拜读后，发现文中的方法并不是想象中的那么方便快捷，故在原文的基础之上作些探讨。

1 对文献1两个例题的研究

例题1 如图1所示，圆弧形货架摆着四个完全相同的光滑小球，O为圆心。则对圆弧面的压力最小的是（ ）

A.a球 B.b球

C.c球 D.d球

参考答案：小球对圆弧面的压力大小等于球的重力沿斜面向下的分力mgsinθ，由图1可知，a球所在处的倾斜角θ（斜面与水平方向的夹角）最小，所以压力最小，故选A 。

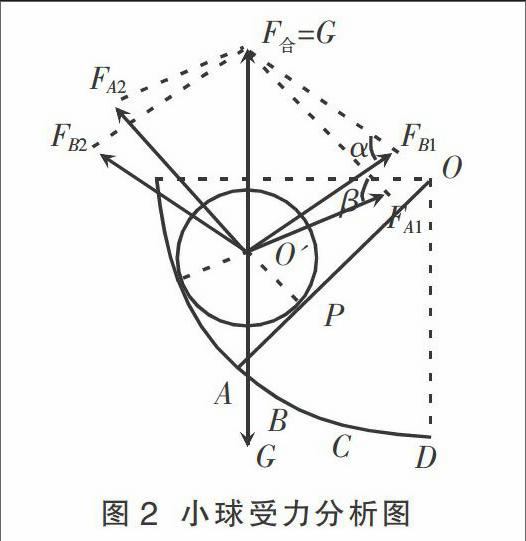
文献1的解答：选项A是正确的答案，但真如解析所说：“小球对圆弧面的压力大小等于球的重力沿斜面向下的分力mgsinθ？把图中的小球放大后，分析受力如图2所示。其中FA1和FA2对应挡板在A点时圆弧面和挡板对球的支持力，从图中可以看出FA1和FA2并不是互相垂直的。显然，参考答案的解析是错误的。有什么办法解决此类问题？现取挡板在图中A、B受力分析，并把FA1和FA2，FB1和FB2各自独立合成后再来分析。

如图2所示，FB1和FB2表示挡板在B点时圆弧面和挡板对球的支持力。在图中∠FA2O'FA1与∠FB2O'FB1是相等的，即图中α、β角是相等的，故4点F■、O'、FA1、FB1共圆。去掉图中其他线条，作出4点所在圆（如图3所示）。主要挡板最低能摆放到竖直位置，即挡板对球的支持力F2不能转到水平位置。由图3可知，当挡板逆时针转动时，点O'在圆周沿FA1和FB1方向移动，其中圆弧对球的支持力不能指向4点确定的圆的直径方向，故圆弧对球的支持力不断增大，挡板对球的支持力不断减小。

点评分析：文献1与参考答案的分歧在于，参考答案把小球看成一个质点，此时小球对圆弧面的压力大小等于球的重力沿斜面向下的分力mgsinθ，从而快速确定答案。而文献1认为小球不能看成质点，适当放大之后，圆弧面对小球的支持力和挡板对小球的支持力并不垂直，因此套用正交分解的结论是错误的。显然，题目中没有说明小球可看成质点，文献1的解法确实更为严谨。但是对于中学生来说，该法费时费力效果不佳。笔者曾把文献1的解法传授给学生，经调查发现，很多学生根本理不清几对线条之间的几何关系，更谈不上巧妙构圆，因此寻找一种更便捷的方法是很有必要的。

笔者的解法：如图4所示，对小球受力分析后可知，小球受到的两个力虽然不垂直，但是当小球缓慢下滑时，两弹力之间的夹角α+β保持不变，可采用拉密定理求解。根据拉密定理，在同一平面内，当三个共点力的合力为零时，其中任一个力与其他两个力夹角正弦的比值相等，■=■，即■=常数。当小球缓慢下移时，α角减小，β角增大， F2逐渐增大，所以圆弧面对a球的支持力最小。根据牛顿第三定律，a球对圆弧面的压力最小。该法的最大好处是避开了复杂的线条关系，用公式进行定量分析，方便快捷。

例题2 如图5所示，杆BC的B端用铰链接于竖直墙上，另一端C为一定滑轮。重物G系一绳经过滑轮固定于墙上的A点，杆恰好平衡。若将绳的A端沿墙稍向下移至A'点，再使之平衡，杆重、滑轮大小及各处摩擦均可省略，则此时滑轮C的位置（ ）

A.在AA'之间 B.与A'点等高

C.在A'点之下 D.在A点之上

文献1的解答：引进“辅助圆”，则解答会变得一目了然。C点总在以B为圆心，BC为半径的圆周上，如图6所示。其中，BC线总是∠ACG的角平分线。根据这个特点，我们可作出各点的位置关系（如图7所示），P和P' 关于BC所在直径对称，直观可见，C的位置在A点之上，故选D。

笔者的解法：对C点受力分析，由于杆一直平衡且两段细绳的拉力相等，因此杆对C点的弹力一定处在两段细绳之间的角平分线上。如图8所示，A点下移时，两段绳之间的夹角减小，角θ跟着减小，所以杆只能往左上边摆动，滑轮的位置升高，故选D。

在分秒必争的考场上，快准狠解题是取得高分的保证。碰到难题时，只能采取化繁为简的策略，而文献1恰恰弄反了，一个比（下转第39页）（上接第37页）较简单的平衡题硬是画圆浪费时间，这种做法笔者不太赞同。

2 小 结

三力动态平衡一直是高考的热点，给学生讲透是很有必要的，但一法通吃各种情形的策略往往繁琐不堪。因此，最好的做法是分门别类，针对不同条件，灵活选用不同的方法。笔者通常给学生总结如下的三种情况：（1）三力平衡时，有一个力是恒力，还有一个力的方向不变，优先考虑图解法判断动态变化；（2）三力平衡时，有一个力是恒力，且其余兩个力之间的夹角保持不变，优先考虑拉密定理判断动态变化；（3）三力平衡时，有一个力是恒力，其余两个力的方向都在变，优先考虑三角形相似判断动态变化。

需要说明的是，不少四力动态平衡问题也可转化成三力平衡问题，上述分类还有挖掘的空间，希望感兴趣的朋友同行试之。

参考文献：

[1]彭立君.利用“辅助圆”巧解一类动态平衡问题[J].物理教学探讨，2016，34（12）：46-47.

（栏目编辑 罗琬华）endprint