新药临床试验设计中的比较类型

谷恒明，胡良平,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu812@sina.com)

新药临床试验设计中的比较类型

谷恒明1，胡良平1,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029
*通信作者：胡良平，E-mail：lphu812@sina.com)

本文目的是介绍新药临床试验设计中的四种比较类型，即一般差异性检验、非劣效性检验、优效性检验和等效性检验。通过讲解与假设检验有关的概念，总结了假设检验的种类，推理出广义差异性检验的概念；着重论述了四种比较类型和合理选用的要领；从临床试验设计角度出发，详细给出了成组设计四种比较类型下一元定量资料假设检验时样本含量估计所需要的SAS程序和应用实例，并提供了与“成组设计四种比较类型有关的其他内容的解决方案”的参考文献。

统计假设；假设检验；差异性检验；非劣效性检验；优效性检验；等效性检验；样本含量

1 与假设检验有关的概念

1.1 假设检验的定义

基于某种统计假设(包括原假设与备择假设)，依据样本资料所提供的信息，在一定可靠程度(1-α)上对原假设作出统计推断：是否拒绝原假设。若拒绝原假设，则选择备择假设；反之，则认为尚无充足的证据拒绝原假设，暂时只能保留原假设(注意：这并不意味着原假设一定成立)。这种统计判决的方法被称为“假设检验”[1]。

统计假设中的“原假设或零假设或无效假设(简记为H0)”通常为研究问题的“一种可能的结果”，数理统计学家据此构造出一个计算公式，即检验统计量(它是无中生有的产物)；再设法“顺藤寻根”，找出理由或证据，从而依据此检验统计量作出接受或拒绝“原假设”的统计推断。一旦拒绝了原假设，自然也就接受了备择假设(简记为H1)。换句话说，备择假设实际上就成了研究问题的“另一种可能的结果”。

第1种情形：两种药物的疗效谁好谁差事先并不清楚，属于双侧检验。其统计假设如下：

H0:μT-μR=0试验组与对照组的总体平均数相等；

H1:μT-μR≠0试验组与对照组的总体平均数不等。

第2种情形：两种药物的疗效谁好谁差事先知道一些初步的信息，而且明确知道T药的疗效可能比R药的疗效差(属于左单侧检验，评价指标为高优指标)。其统计假设如下：

H0:μT-μR≥0试验组的总体平均数大于或等于对照组的总体平均数；

H1:μT-μR<0试验组的总体平均数小于对照组的总体平均数。

第3种情形：两种药物的疗效谁好谁差事先知道一些初步的信息，而且明确知道T药的疗效可能比R药的疗效好(属于右单侧检验，评价指标为高优指标)。其统计假设如下：

H0:μT-μR≤0试验组的总体平均数小于或等于对照组的总体平均数；

H1:μT-μR>0试验组的总体平均数大于对照组的总体平均数。

第4种情形：两种药物的疗效谁好谁差事先知道一些初步的信息，而且明确知道T药的疗效可能比R药的疗效差，但其差值可能不会超出专业上允许的一个界值(属于右单侧检验，评价指标为高优指标；其界值被称为非劣效界值，常取负值)。其统计假设如下：

H0:μT-μR≤δL试验组的总体平均数与对照组的总体平均数之差小于或等于δL，即试验组劣效于对照组；

H1:μT-μR>δL试验组的总体平均数与对照组的总体平均数之差大于δL，即试验组非劣效于对照组。

第5种情形：两种药物的疗效谁好谁差事先知道一些初步的信息，而且明确知道T药的疗效可能比R药的疗效好，并且其差值可能会超出专业上允许的一个界值(属于右单侧检验，评价指标为高优指标；其界值被称为优效界值，常取正值)。其统计假设如下：

H0:μT-μR≤δU试验组的总体平均数与对照组的总体平均数之差小于或者等于δU；

H1:μT-μR>δU试验组的总体平均数与对照组的总体平均数之差大于δU。

第6种情形：两种药物的疗效谁好谁差事先知道一些初步的信息，而且明确知道T药的疗效可能比R药的疗效略好一些；但也可能T药的疗效比R药的疗效略差一些，并且其差值的绝对值可能不会超出专业上允许的一个界值(属于双单侧检验，评价指标为高优指标；其界值被称为等效界值)。其统计假设如下：

H0(1):μT-μR≤δL试验组的总体平均数与对照组的总体平均数之差小于或等于δL；

H1(1):μT-μR>δL试验组的总体平均数与对照组的总体平均数之差大于δL；

H0(2):μT-μR≥δU试验组的总体平均数与对照组的总体平均数之差大于或等于δU；

H1(2):μT-μR<δU试验组的总体平均数与对照组的总体平均数之差小于δU。

注意：δL取负值、δU取正值，它们的绝对值可以相等，也可以不等。具体取什么值，取决于具体问题的专业知识，应由多位同行专家共同讨论后决定。

1.2 假设检验的种类

1.2.1 概述

从宏观角度来划分，假设检验的种类可粗分为：对总体参数的假设检验、对总体分布的假设检验、对总体中某些属性之间关联性的假设检验和对总体中某种统计模型的假设检验等。

1.2.2 具体分类

1.2.2.1 对总体参数的假设检验

对总体均值、总体标准差、总体方差、总体率、总体变异系数、总体中位数等的假设检验，都属于对总体参数的假设检验。

1.2.2.2 对总体分布的假设检验

假定从某特定的总体中随机抽取样本含量为n个个体，测定每个个体的某定量指标的数值。在对该组定量资料进行多种统计分析之前，常需要检查该资料是否取自正态分布的总体。此时的统计假设为：

H0：该组定量资料取自正态分布的总体；

H1：该组定量资料取自非正态分布的总体。

在对多组生存时间资料采用Kaplan-Meier方法构建出多条生存率曲线后，需要比较它们之间的差别是否具有统计学意义时，SAS中的LIFETEST过程会给出三种假设检验方法(对数秩检验、威尔科克森检验、似然比检验)计算的结果，有时这三种结果并非完全一致，甚至会出现统计结论矛盾的结果(即P值大于或小于0.05的两类结果)。此时，选择哪种假设检验方法的结果来下结论，取决于生存时间t的分布情况[3]。若能通过假设检验得到当前的生存资料服从某种特定的分布(如指数分布或对数正态分布或威布尔分布)，就可选择似然比检验或威尔科克森检验或对数秩检验。

1.2.2.3 对总体中某些属性之间关联性的假设检验

在考察定性原因变量对定性结果变量影响时，若采用差异性检验，常选用χ2检验。而此种检验的统计假设如下：

H0：两种属性之间互相独立；

H1：两种属性之间不互相独立。

1.2.2.4 对总体中某种统计模型的假设检验

一般来说，基于样本数据构建的因变量依赖自变量变化的关系式被称为回归方程，而它对应的总体中的关系式被称为统计模型或回归模型。由回归方程去推论统计模型是否成立，就是对统计模型的假设检验。通常要求：统计模型和模型中各参数的假设检验结果都具有统计学意义时，才认为此统计模型是基本可用的。至于此统计模型是否具有实用价值，还应结合具体问题和专业知识对其作进一步考察和验证。

1.3 广义差异性检验

1.3.1 概述

差异性检验可用于两者或多者之间的比较，但更多场合下用于两者(两个同类参数，如总体平均值、总体方差，两条生存率曲线)之间的比较。特别是在两者之间比较时，根据具体情况又可分为：若仅关注两者之间的差量与“0”之间的差别是否具有统计学意义，它被称为一般差异性检验；若关注两者之间的差量与“非0的常量”之间的差别是否具有统计学意义，它被称为三种特殊的差异性检验，包括非劣效性检验、优效性检验和等效性检验。除此之外，还有一些假设检验方法，从字面上看，它们并非叫“差异性检验”。如：一致性检验、独立性检验、相关性检验、对称性检验、正态性检验等，但在本质上，它们仍属于差异性检验。事实上，在统计学上，绝大多数假设检验方法都属于差异性检验，故将假设检验方法统称为“广义差异性检验”是比较适当的。

1.3.2 四种比较类型的基本概念

1.3.2.1 一般差异性检验

一般差异性检验是指主要研究目的为显示两种(或多种)处理方法的效应之差量与“0”之间的差别是否具有统计学意义的检验。在试验设计阶段不需要设定任何界值。

1.3.2.2 非劣效性检验

非劣效性检验是指主要研究目的为显示试验药的治疗效果在临床上不比阳性对照药差的检验。在试验设计阶段需要设定一个界值 ，来界定试验药是否不比阳性对照药疗效差过预先设定的这个界值。在实际使用时， 取负值表示“方向”，即在疗效指标为高优指标时，治疗药的效应指标的取值小于阳性药的效应指标的取值，这是一个单侧检验。

1.3.2.3 等效性检验

等效性检验是指主要研究目的为显示两种治疗效果之间的差别大小在临床上并无重要意义的检验。在试验设计阶段需要设定等效性界值(δL，δU)来界定两种治疗的等效性。这是一个双单侧检验，其中，δL常取负值、δU取正值。

1.3.2.4 优效性检验

优效性检验是指主要研究目的为显示试验药的治疗效果优效于对照药(安慰剂对照或阳性对照)的检验。在试验设计阶段需要设定一个界值δU，来界定试验药的优效性。δU取正值，表示“方向”，即在疗效指标为高优指标时，治疗药的效应指标的取值大于阳性药的效应指标的取值，这是一个单侧检验。

2 合理选择四种比较类型的要领

2.1 选择差异性检验的理由与场合

2.1.1 选择双侧差异性检验的理由与场合

当预试验的结果表明，试验药与对照药效果接近，而且两者之间的效应指标的差量取正值还是负值尚不能确定。此时，当研究目的是考察试验药与对照药疗效之差量与“0”之间的差别是否具有统计学意义(没有设定有临床意义的界值)，选用双侧差异性检验。

2.1.2 选择左单侧差异性检验的理由与场合

当预试验的结果表明，试验药的疗效总比对照药的疗效稍差一些，但差量并非足够大。此时，当研究目的是考察试验药与对照药疗效的差量是否具有统计学意义(没有设定有临床意义的界值)，选用左单侧差异性检验。

2.1.3 选择右单侧差异性检验的理由与场合

当预试验的结果表明试验药的疗效总比对照药的疗效稍好一些，但差量并非足够大。此时，当研究目的是考察试验药与对照药疗效的差量是否具有统计学意义(没有设定有临床意义的界值)，选用右单侧差异性检验。

2.2 选择非劣效性检验的理由与场合

当预试验的结果表明虽然试验药的效果比对照药效果略差一些，但两者之间的效应指标的差量在数量上并非足够大，结合临床专业知识可知，此差量尚达不到具有临床实际意义的界值。此时，为显示试验药的治疗效果在临床上不比阳性对照药差，选用非劣效性检验。在试验设计阶段设定了一个有临床意义的界值 ，来界定试验药是否不比阳性对照药疗效差过预先设定的这个界值。

2.3 选择等效性检验的理由与场合

当预试验的结果表明试验药的效果不会比对照药效果好很多，也不会差很多。而且，两者之间的效应指标的差量的绝对值在数量上并非足够大，结合临床专业知识可知，此差量的绝对值将小于具有临床实际意义的界值。此时，为显示两种治疗药物之间的差别大小在临床上并无重要意义，选用等效性检验。在试验设计阶段设定了两个有临床意义的等效性界值(δL，δU)来界定两种治疗的等效性。

2.4 选择优效性检验的理由与场合

当预试验的结果表明试验药的效果不仅比对照药效果好，而且两者之间的效应指标的差量在数量上相当可观，结合临床专业知识可知，此差量具有临床上的实际意义。此时，为了通过正式临床试验，显示试验药的治疗效果优效于对照药(安慰剂对照或阳性对照)，选用优效性检验。在试验设计阶段设定了一个有临床意义的界值 ，来界定试验药的优效性。

3 成组设计四种比较类型下样本含量估计[2]

3.1 成组设计四种比较类型下一元定量资料假设检验时样本含量估计

【例1】某研究者观察氯沙坦与伊贝沙坦治疗对伴高尿酸血症的原发性高血压患者血清尿酸水平的影响并评价其降压疗效，假定“氯沙坦”为试验药、“伊贝沙坦”为对照药。拟采用多中心、随机、双盲、平行对照设计，主要疗效指标为“治疗6周后收缩压改变值”，并使用双侧差异性检验评价两种药物的降压效果的差别是否具有统计学意义。现取α=0.05，β=0.20，由预试验得到两药各自的平均疗效及标准差的数值见表1，并假定两药物组样本含量之比为1∶1，试估计该试验所需的样本量。

表1 两组患者治疗6周后收缩压下降幅度(mmHg)

【解答】这属于成组设计一元定量资料一般差异性双侧检验时样本含量估计问题，使用下面的SAS程序计算，可得到两组各需要226例受试对象，实际的检验效能约为80.14%。

%let x_bar_t=13.29;%let x_bar_r=14.87;%let s_t=6.10;%let s_r=5.84;

%let alpha=0.05;%let beta=0.20;%let n_max=10000;

data clinic10_1;

do n_r=2 to &n_max;

n_t=n_r;

power=probt((&x_bar_t-&x_bar_r)/sqrt((1/n_t+1/n_r)*((n_t-1)*&s_t**2+(n_r-1)*&s_r**2)/(n_t+n_r-2))-tinv(1-&alpha/2,n_t+n_r-2),n_t+n_r-2)+probt(-(&x_bar_t-&x_bar_r)/sqrt((1/n_t+1/n_r)*((n_t-1)*&s_t**2+(n_r-1)*&s_r**2)/(n_t+n_r-2))-tinv(1-&alpha/2,n_t+n_r-2),n_t+n_r-2);

if power>=1-&beta then goto ok;

end;

ok:n_t=n_r;

run;

ods html;

proc print noobs;

var n_t n_r power;

run;

ods html close;

值得注意的是：若预计进行临床试验研究过程中将有15%的脱落率(即有15%的入选者中途可能会退出临床试验)，应将其考虑进去。具体地说，所需要的样本含量为：

(226+226)/(1-0.15)=532，即每组需要266例受试对象。

【例2】沿用例1中大多数信息，假定“氯沙坦”为试验药、“伊贝沙坦”为对照药，将拟解决的问题修改为：使用左单侧差异性检验评价两种药物的降压效果的差别(关注氯沙坦的疗效指标的总体平均值是否小于伊贝沙坦的疗效指标的总体平均值)是否具有统计学意义。

【解答】这属于成组设计一元定量资料一般差异性左单侧检验时样本含量估计问题，只需将例1中SAS程序做如下修改：

修改位置在“power=”的右边有两处“tinv(1-&alpha/2,n_t+n_r-2)”，将其修改为：“tinv(1-&alpha,n_t+n_r-2)”。所得计算结果为：

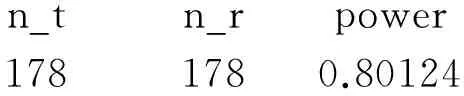
n_tn_rpower1781780.80124

即每组需要178例受试者。同理，若考虑15%的脱落率，每组需要210例受试者。

【例3】沿用例1中大多数信息，假定“伊贝沙坦”为试验药、“氯沙坦”为对照药，将拟解决的问题修改为：使用右单侧差异性检验评价两种药物的降压效果的差别(关注伊贝沙坦的疗效指标的总体平均值是否大于氯沙坦的疗效指标的总体平均值)是否具有统计学意义。

【解答】这属于成组设计一元定量资料一般差异性右单侧检验时样本含量估计问题，只需将例1中SAS程序做如下修改：

第1处：将例1中SAS程序第1行平均值与标准差的位置替换：

%let x_bar_t=14.87;%let x_bar_r=13.29;%let s_t=5.84;%let s_r=6.10;

第2处：修改位置在“power=”的右边有两处“tinv(1-&alpha/2,n_t+n_r-2)”，将其修改为“tinv(1-&alpha,n_t+n_r-2)”。所得计算结果为：

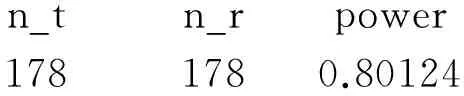
n_tn_rpower1781780.80124

即每组需要178例受试者。同理，若考虑15%的脱落率，每组需要210例受试者。

【例4】沿用例1中大多数信息，假定“氯沙坦”为试验药、“伊贝沙坦”为对照药，并假定非劣效性界值为“δL=-3.0mmHg”(注意：非劣效性界值必须由多位同行专家充分讨论后确定，才具有权威性，以至于达到一定程度上的合理性)，将拟解决的问题修改为：使用非劣效性检验评价试验药在降压效果上是否非劣效于对照药，即在给定的非劣效性界值(δL=-3.0)前提条件下，关注氯沙坦的疗效指标的总体平均值是否不小于伊贝沙坦的疗效指标的总体平均值。

【解答】这属于成组设计一元定量资料非劣效性检验时样本含量估计问题，所需要的SAS程序如下：

%let x_bar_t=13.29;%let x_bar_r=14.87;%let s_t=6.10;%let s_r=5.84;%let delta_L=-3.0;

%let alpha=0.05;%let beta=0.20;%let n_max=10000;

data clinic10_4;

do n_r=2 to & n_max;

n_t=n_r;

power=probt(((&x_bar_t-&x_bar_r)-&delta_L)/sqrt((1/n_t+1/n_r)*((n_t-1)*&s_t**2+(n_r-1)*&s_r**2)/(n_t+n_r-2))-tinv(1-&alpha,n_t+n_r-2),n_t+n_r-2);

if power>=1-&beta then go to ok;

end;

ok:n_t=n_r;

run;

ods html;

proc print noobs;

var n_t n_r power;

run;

ods html close;

计算结果如下：

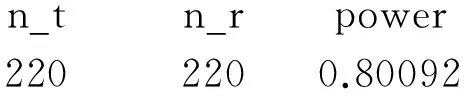
n_tn_rpower2202200.80092

即每组需要220例受试者。同理，若考虑15%的脱落率，每组需要259例受试者。

【例5】沿用例1中大多数信息，假定“伊贝沙坦”为试验药、“氯沙坦”为对照药，并假定优效性界值为“δU=0.5mmHg”(注意：优效性界值必须由多位同行专家充分讨论后确定，才具有权威性，以至于达到一定程度上的合理性)，将拟解决的问题修改为：使用优效性检验评价试验药在降压效果上是否优效于对照药，即在给定的优效性界值(δU=0.5)前提条件下，关注伊贝沙坦的疗效指标的总体平均值是否大于氯沙坦的疗效指标的总体平均值。

【解答】这属于成组设计一元定量资料优效性检验时样本含量估计问题，将例4中的SAS程序做如下修改：

第1处：第1行程序需做如下修改：

%let x_bar_t=14.87;%let x_bar_r=13.29;%let s_t=5.84;%let s_r=6.10; %let delta_U=0.5;

第2处：“power=”右边需做如下修改：

将“&delta_L”修改为“&delta_U”。

所得结果如下：

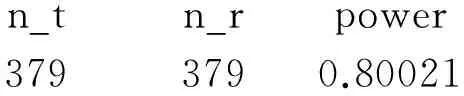
n_tn_rpower3793790.80021

即每组需要379例受试者。同理，若考虑15%的脱落率，每组需要446例受试者。

【例6】沿用例1中大多数信息，假定“氯沙坦”为试验药、“伊贝沙坦”为对照药，并假定等效性界值为“δL=-3.0mmHg、δU=3.0mmHg”(注意：两个等效性界值必须由多位同行专家充分讨论后确定，才具有权威性，以至于达到一定程度上的合理性，左右界值的绝对值可以不等)，将拟解决的问题修改为：使用等效性检验评价试验药在降压效果上是否等效于对照药，即在给定的等效性界值(δL=-3.0、δU=3.0)前提条件下，关注氯沙坦的疗效指标的总体平均值是否等于伊贝沙坦的疗效指标的总体平均值。

【解答】这属于成组设计一元定量资料等效性检验时样本含量估计问题， 所需要的SAS程序如下：

%let x_bar_t=13.29;%let x_bar_r=14.87;%let s_t=6.10;%let s_r=5.84;

%let delta_L=-3.0;%let delta_U=3.0;

%let alpha=0.05;%let beta=0.20;%let n_max=10000;

data clinic10_5;

do n_r=2 to & n_max;

n_t=n_r;

power=probt((-&delta_L+(&x_bar_t-&x_bar_r))/sqrt((1/n_t+1/n_r)*((n_t-1)*&s_t**2+(n_r-1)*&s_r**2)/(n_t+n_r-2))-tinv(1-&alpha/2,n_t+n_r-2),n_t+n_r-2)+probt((&delta_U-(&x_bar_t-&x_bar_r))/sqrt((1/n_t+1/n_r)*((n_t-1)*&s_t**2+(n_r-1)*&s_r**2)/(n_t+n_r-2))-tinv(1-&alpha/2,n_t+n_r-2),n_t+n_r-2)-1;

if power>=1-&beta then go to ok;

end;

ok:n_t=n_r;

run;

ods html;

proc print noobs;

var n_t n_r power;

run;

ods html close;

所得结果如下：

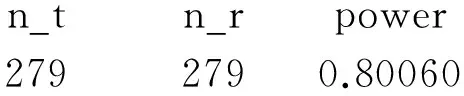
n_tn_rpower2792790.80060

即每组需要279例受试者。同理，若考虑15%的脱落率，每组需要329例受试者。

3.2 成组设计四种比较类型下一元定性资料假设检验时样本含量估计

与上节类似，成组设计四种比较类型下一元定性资料假设检验时样本含量估计也可以有6种不同的情形，需要时，读者可参阅文献[2]“第十一章成组设计定性资料四种比较类型所需样本含量的计算”。因篇幅所限，此处暂不赘述。

4 成组设计四种比较类型下一元定量资料与定性资料假设检验时检验效能估计

因篇幅所限，成组设计四种比较类型下一元定量资料与定性资料假设检验时检验效能估计的具体方法和应用实例，请参阅文献[2]“第十二章和第十三章”，此处从略。

5 成组设计四种比较类型下一元定量资料与定性资料的假设检验

因篇幅所限，成组设计四种比较类型下一元定量资料与定性资料的假设检验的具体方法和应用实例，请参阅文献[2]“第八章和第九章”，此处从略。

[1] 茆诗松. 统计手册[M]. 北京: 科学出版社, 2003: 76-82.

[2] 胡良平, 陶丽新. 临床试验设计与统计分析[M]. 北京: 军事医学科学出版社, 2013: 71-134.

[3] 胡良平. 面向问题的统计学——(1)科研设计与统计基础[M]. 北京: 人民卫生出版社, 2012: 397-406.

(本文编辑：陈 霞)

Comparative type in the design of clinical trials for a new drug

GuHengming1,HuLiangping1,2*

(1.ConsultingCenterofBiomedicalStatistics,AcademyofMilitaryMedicalSciences,Beijing100850,China;2.SpecialtyCommitteeofClinicalScientificResearchStatisticsofWorldFederationofChineseMedicineSocieties,Beijing100029,China*Correspondingauthor:HuLiangping,E-mail:lphu812@sina.com)

The article aimed to introduce four kinds of the comparative types in the design of clinical trials for a new drug, such as general difference test, non-inferiority test, superiority test and equivalence test. The author summarized many kinds of hypotheses and deduced the concept of the generalized difference test by explaining the concepts related to the hypothesis test, and also focused on four comparative types and their rational applications. Started from the view of the clinical trial design, the authors presented the SAS programs and applied examples which involved the sample size determination for the situation mentioned above, and also provided the references to "solutions for other contents related to the four comparative types of two group parallel design".

Statistical hypothesis; Hypothesis test; Difference test; Non-inferiority test; Superiority test; Equivalence test; Sample size

国家高技术研究发展计划课题资助(2015AA020102)

R195.1

A

10.11886/j.issn.1007-3256.2017.04.005

2017-08-13)