在大学物理课程中嵌入数值计算的捷径
刘兆龙 胡海云
(北京理工大学物理学院,北京 100081)
在大学物理课程中嵌入数值计算的捷径
刘兆龙 胡海云
(北京理工大学物理学院,北京 100081)
数值计算已经成为研究复杂系统物理规律时不可缺少的手段,但基于各个方面的困难,它很难在大学物理课程中有所体现。本文介绍了借助Excel软件将数值计算嵌入大学物理课程的方法,给出了利用Excel软件实现可视化、数值积分和求微分方程数值解的方法。文中所述的方法简捷易行,可操作性强,且不必耗费大量学时,非常适用于面向低年级理工科学生的大学物理课程。采用此方法,可以使低年级学生较早地熟悉数值计算,更好地掌握物理知识和应用物理知识解决问题,是大学物理课程教学改革的一种有益尝试。
大学物理;数值计算;教学改革;Excel
1 背景
伴随着计算机技术的不断进步,数值计算已经被公认为是研究复杂系统物理规律时不可缺少的手段,也成为了高校物理教学的重要内容之一。从20世纪80年代起,国内外大学的物理系陆续开设了计算物理学课程,教授物理专业的学生利用数值计算方法去解决问题。说到物理教育与教学,受众最广的群体是非物理专业的学生,特别是理工科学生,其群体数量远远大于物理专业的学生。在面向该群体的大学物理课程中,数值计算一直没有像近代物理那样得到大规模的普及。如何将计算物理学普物化,即将计算物理学的研究方法引入面向非物理专业的理工科大学物理课程甚至是文科物理课程中,将之与原有教学内容有机结合,加强大学物理课程的应用性,使大学物理课程更现代化,是一个值得研究的课题,也是大学物理课程教学的改革方向之一。
现今,随着各校教学设施的改善和手提电脑的日益普及,实施计算物理普物化的时机日益成熟,其主要困难在于计算软件的使用。大学物理课程面向低年级学生,学生们的编程能力和计算机语言基础普遍有限,而教师不能在物理课上花费大量课时讲解编程,这一矛盾是计算物理普物化的困难之一。此外,对大部分学生来说,大学物理学课程本身难度相对较大,如果再花费很多时间用于编程,会增加学生的学习负担或减少用于物理知识本身的学习时间,有喧宾夺主之忧。
2 Excel及其在大学物理课程数值计算中的应用
很显然要在大学物理中引入数值计算,需要借助相对易学的通用软件,在现有的教学框架中有机地融入计算物理学的思想与方法,凸显数值计算的魅力,使低年级学生较快地解决一些“相对复杂”的问题。国外大学物理课程中已经在此方向进行了有益的尝试[1]。目前可用于科学计算的软件较多,例如Matlab, Mathematic, Maple, Python计算平台等,但是使用这些软件需要学生们学习程序设计语言,并且学生们在高中时很少接触它们。
Microsoft Excel是微软公司Microsoft office的组件之一,是一款功能强大的电子表格处理软件,包含大量公式和函数,可以执行计算。许多教师对于此软件并不陌生,常用之统计学生成绩或在大学物理实验课上处理实验数据,而且有些学生在高中的信息技术课上接触过Excel。将此软件用于低年级本科生的大学物理课程之中,可以起到事半功倍的作用,使得我们可以基于传统大学物理课程的知识框架,回避对学生进行系统地编程训练,帮助学生了解建立模型、设计计算方法、编程和结果分析这一计算物理学研究问题的过程,并进行简单应用。它还有助于学生对物理现象和规律的理解。
下面通过大学物理课程中几个常见的实例,看如何使用Excel实现数值计算。
2.1 在大学物理课程中实现“可视化”

使用Excel软件,可以轻松地解决这个问题,即使对于没有学过编程或专门的计算机语言的学生,也能快速掌握曲线的作图方法,独立绘出漂亮的函数图线,并利用它探究其中的物理知识。
例如要绘制氧气在0℃时的麦克斯韦速率分布曲线,完成步骤为

图1 利用Excel完成的麦克斯韦速率分布曲线(截取了局部工作表)。绘制其他气体曲线时,只要在C2单元格中输入相应的质量。在C3单元中输入不同的数值,可以得到不同温度下的分布曲线。为了便于比较,图中给出了温度为T和T/2的两条曲线
• 新建Excel工作表,在第一行中敲入注释,解释此工作的内容,如:麦克斯韦速率分布函数,如图1。在A2单元格中输入文字“输入质量:”,C2单元中敲入氧气分子的质量5.32E-26,并在名称框中将该单元的名称定义为m,随后在D2单元格中输入其单位kg。依此法在第3、4和5 行中分别输入温度、温度的步长值和玻尔兹曼常数,名称分别定义为T、DELTA和k。若要研究其他气体,只要直接在C2单元格中敲入其分子或原子质量的数值即可。要改变温度,也只需在C3单元格中直接敲入所需数值。同理,改变C4的数值就可以改变温度的步长
• 建立表头,如速率、速率分布函数等,见图1中的第7行

图2 利用Excel完成的拍频绘图(截取了局部工作表)
• 在A列中输入速率。例如若速率范围是0~1200m/s,步长为25m/s,则在A8单元格中输入0,A9单元格中输入=A8+DELTA,将鼠标放在A9的右下角,当鼠标成黑十字星时,按住鼠标的左键竖直向下拖拽(本文中将此操作简称为竖直向下拖拽鼠标),直至速率到达1200m/s,即设置好了速率的取值
• 在B8单元中输入麦克斯韦速率分布函数=4*3.14*(m/(2*3.14*k*T))^(3/2)*A8^2*EXP(-m*A8^2/(2*k*T))
• 从B8单元格的右下角竖直向下拖拽鼠标,完成第B列各单元格的计算
• 选中A、B列中所有数据,点击工具栏中的绘图按钮,选择绘制XY散点图,得到曲线
• 编辑曲线,加上说明文字,完成曲线绘制,见图1
利用这个小小的程序,可以进行许多教学讨论。例如:温度、质量、速率区间、步长等量的变化对曲线形状的影响;以及数值计算中如何处理无限大等。还可以计算各个速率区间内的分子数占总分子数的百分比,并绘出相应的分布,见图1中最右侧的图。
采用相同的方法可以很容易地绘出许多曲线,例如拍频(图2)、李萨如图形(图3)、单缝衍射光强曲线(图4)、普朗克黑体辐射曲线(图5)等许多曲线,在此不做更多的赘述。对于学习大学物理课程的低年级学生来说,用Excel实现的初级可视化易学、好用。
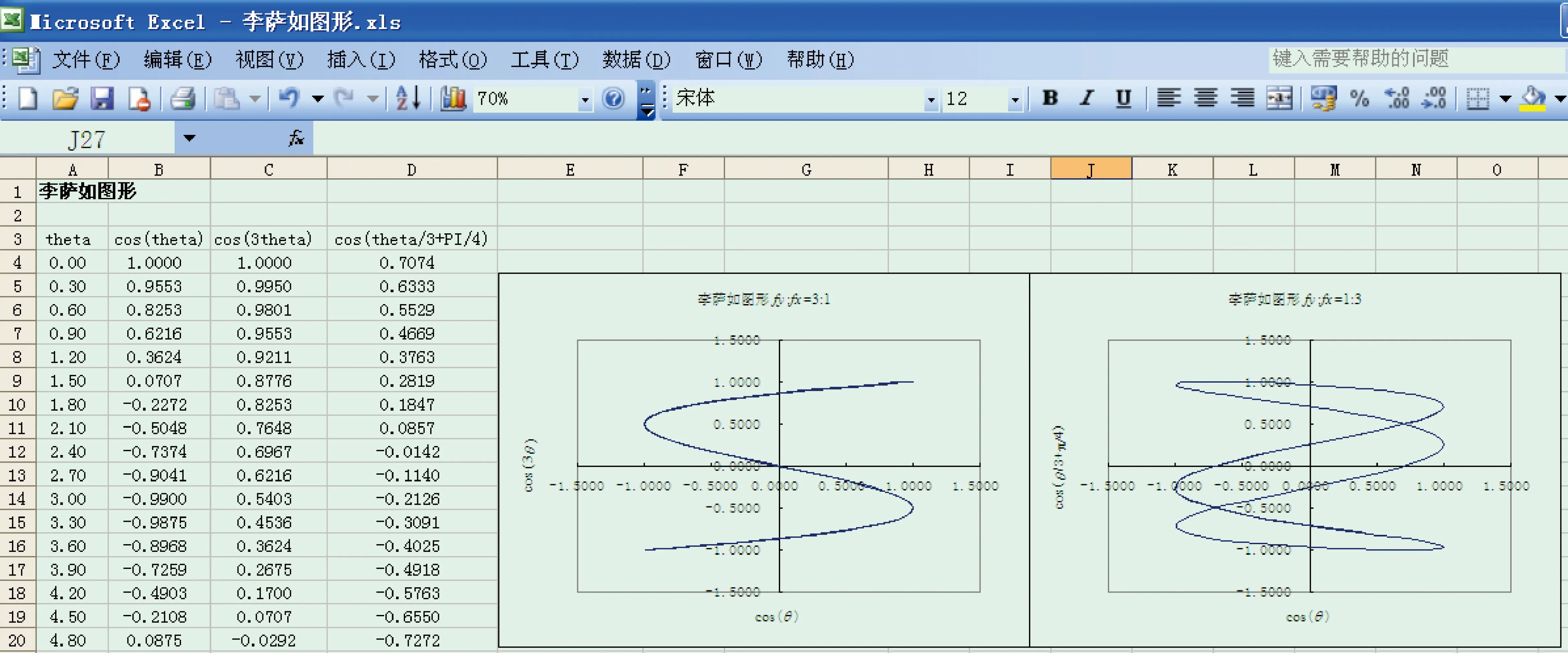
图3 利用Excel完成的李萨如图形(截取了局部工作表)

图4 利用Excel完成的单缝衍射光强曲线(截取了局部工作表)

图5 普朗克黑体辐射曲线(截取了局部工作表)
2.2 利用Excel做积分
积分是大学物理课程中常用的计算,有些积分难以使用现成的积分公式,需要做数值计算。这一点限制了教材中的例题和习题的设置。使用Excel可以解决此困难。例如:某容器内装有温度为T=300K的氦气,系统处于平衡态。已知其中的原子个数为N=106,原子的质量为m=6.65×10-27kg,求: (1)速率区间vp~vp+40m/s内的原子个数,(2)速率区间10vp~10vp+40m/s内的原子个数,vp为最概然速率。
可以利用Excel,练习数值计算中的梯形法积分法。很容易算出vp=1120m/s,要计算所求速率区间内的原子数DN,需计算积分
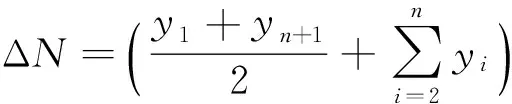
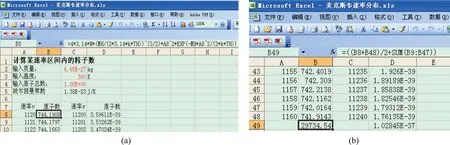
图6 利用Excel做数值积分
• 新建Excel文件,设置原子质量MH、温度TH、原子总数N和玻尔兹曼常数k,并定义它们的名称,如图6(a)。根据积分范围,在A和C列中分别输入所需,即速率
• 在B8和D8单元格中输入被积函数=4*3.14*N*(MH/(2*3.14*k*TH))^(3/2)*A8^2*EXP(-MH*A8^2/(2*k*TH))
• 将鼠标放置在B8单元格的右下角向下拖拽,计算出各个节点处的y值。在D列重复此操作
• 在B和D列已有数值下方的单元格中输入计算ΔN的公式,完成积分,如图6(b)
由B49单元中的值可知第1问的结果为30000个,由D49单元中的值可以得到第2问的结果是:原子基本上不出现在这个区间内。
在此基础上,可改变质量、温度、原子数、速率区间等量,得到所需的积分值。还可改变步长,讨论它对计算结果的影响。可以看出,将解析解和数值解混搭,扩大了解决问题的范围。
2.3 利用Excel解微分方程
Excel可用于解一些简单的微分方程,使学生们了解有关数值计算的简单知识。以阻尼振动为例。方程为:
(1)
设ω0=20s-1,对于欠阻尼,取阻尼系数β1=3s-1;对过阻尼,取β2=40s-1。初始条件为:t=0,x0=A0=0.3×10-2m,初速度v0=0。对应该初始条件的解析解为
(2)
(3)
(4)
(5)
对于欠阻尼,用Excel实现计算的步骤为:
• 新建Excel文件,设置时间步长(名称定义为DELTA)、初始条件、阻尼系数b、ω0等量的名称和数值等,在第D6中敲入=SQRT(OMEGA0^2-BETA1^2),也就是式(3),计算ω的值,并定义其名称
• 在第10行中输入各个变量的名称,如T、x、y等,如图7
• 在A11、B11、C11、D11单元格中分别输入各个量的初值
• A12单元格中输入=A11+DELTA,并竖直拖拽鼠标,在A列中完成时间的数据输入
• B12单元中输入式(2),C12单元内输入式(4),在D12单元内输入式(5)

图7 利用Excel解阻尼振动微分方程图中x0为欠阻尼的解析解;x、 x1 和x2分别为欠阻尼、临界阻尼和过阻尼的数值解。图中欠阻尼的数值解幅度大于其解析解
• 同时选中B12、C12和D12单元,用鼠标向下拖拽,拖拽的同时观察x的值,当它趋于零时,停止拖拽,完成计算
• 同时选中B、C、D列,点击工具栏的绘图按钮,选择XY散点图,得图7
• 添加文字,编辑所得图线
通过上述步骤,采用迭代法,利用Excel解出了这个微分方程,并绘制出振动曲线,见图7右侧。将数值解与解析解进行对照,可验证数值解的正确性。还可对步长、频率等量进行讨论,看曲线如何变化,如何影响数值解的精确度等。Excel解微分方程的步骤和迭代法的应用很直观。利用这种方法,学生还可以研究有空气阻力时抛体的运动和行星轨道等等一些问题。
可以看出,将Excel软件移植进大学物理课程,进行数值计算并非难事,除了上面提到的用途外,还可以用来解n次幂方程、非线性方程和线性方程组等。
3 对教学的促进
利用Excel将数值计算移植到大学物理课程教学的优势是简单易行并且行之有效的。对于低年级学生来说,它可提供一种解决问题的方便工具,扩大了解决问题的范围,并且可以借助它更好地理解物理。对于教师来说,它丰富了讲授方法,使得教学更加直观生动。此外,它还给大学物理的教材编写和习题配置带来新的生机。例如;在国外一些大学物理教材中,数值计算已经进入课后习题,成为常规的作业题目[1]。
说到在大学物理课程中引入数值计算,我国的物理教育工作者已经在此方向进行了有益的探索,例如采用C语言或计算平台[2]、Matlab[3]来实现等。相比于这些软件,Excel功能差一些,如不能实现三维绘图以及动画等。但是,它秉承了“所见即所得”的微软Windows系统理念,简单、易学,可以很轻松地融入现有的大学物理教学体系之中,适用于低年级理工科学生,甚至是文科学生,是在大学物理课程中普及数值计算的得力工具。
4 结语
借助Excel在大学物理课程中实现数值计算对于教师和学生来说都是简单易行的,是在大学物理课程中嵌入数值计算的一条捷径。尽管Excel的功能有限,但是对于面向低年级学生的大学物理课程来说,它能够处理课程中所需的常用计算,并且不耗费很多课时。打个比方来说,如果我们要去远方旅行,自驾、高铁、飞机是我们常常要考虑的出行工具,但是如果我们要在附近活动时,选择骑自行车往往是明智之举。
[1] Paul A.Tipler. Physics for scientists and engineers. Six Edition[M]. New York: W.H.Freeman and Company, 2008.
[2] 李元杰,陆果. 大学物理学[M].2版.北京:高等教育出版社, 2008.
[3] 周群益,侯兆阳,刘让苏. Matlab可视化大学物理学[M].北京:清华大学出版社,2011.
■
A SIMPLE WAY TO EMBED NUMERICAL CALCULATIONS INTO INTRODUCTORY PHYSICS COURSES
Liu Zhaolong Hu Haiyun
(School of Physics, Beijing Institute of Technology, Beijing 100081)
Numerical calculation is an indispensable means to study complex physics systems, but it is difficult to be reflected in the course of introductory physics due to various reasons. This paper introduces the method of embedding numerical calculation into introductory physics curriculum by using Excel software. It shows how to do visualization, numerical integration and solve numerical differential equations by Excel. The method described in this paper is simple, easy to operate, and does not need to spend a great deal of teaching hours. It is very suitable for introductory physics courses designed for junior college students. This method is aimed at helping the lower grade students know the numerical calculation earlier and learn physics more effectively, it also helps students relate what they are learning to real-world problems. It is a useful attempt on the teaching reform of the introductory physics courses.
introductory physics course; physics education; teaching reform; Excel
2017-06-14
刘兆龙,女,教授,主要从事大学物理教学和材料物理方面的研究,zlliu@bit.edu.cn。
刘兆龙,胡海云. 在大学物理课程中嵌入数值计算的捷径[J]. 物理与工程,2017,27(5):71-76.

