BDS/GPS组合天顶对流层延迟估计的精度分析

唐龙江，徐爱功，徐宗秋，2，李 磊

(1.辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2.武汉大学 卫星导航定位技术研究中心，武汉 430079)

BDS/GPS组合天顶对流层延迟估计的精度分析

唐龙江1，徐爱功1，徐宗秋1，2，李 磊1

(1.辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2.武汉大学 卫星导航定位技术研究中心，武汉 430079)

为了详细分析BDS/GPS组合ZTD的精度，选取8个MGEX跟踪站2014年6月至9月的观测数据，利用精密单点定位法分别在未固定跟踪站坐标和固定跟踪站坐标的情况下估计BDS ZTD、GPS ZTD和BDS/GPS组合ZTD，并与IGS提供的对流层产品进行对比分析。实验结果表明：BDS ZTD现阶段的标准差优于34 mm，GPS ZTD与BDS/GPS组合现阶段的标准差相当，均优于14 mm；与未固定跟踪站情形下估计的BDS ZTD相比，固定跟踪站坐标的方式虽然可以提高利用BDS估计ZTD的稳定性，但不能提高精度。

BDS/GPS组合；天顶对流层延迟；精密单点定位；IGS对流层产品

0 引言

在利用全球卫星导航系统(global navigation satellite system，GNSS)估计天顶对流层延迟(zenith tropospheric delays，ZTD)的基础上，可以进一步获得大气水汽含量。利用GNSS估计天顶对流层延迟的方法主要有双差网解法和非差法。与非差法相比，虽然差分法是目前ZTD估计中常用的方法[1-2]，但对于长距离观测值的绝对ZTD估计需要引入与测站相距大于500 km的参考站[3-4]，而且为了取得预期的精度，必须有一定的时间间隔，一般为30 min[5]。随着误差改正模型的精细化和整周模糊度算法的改进，利用非差法估计的ZTD精度与利用差分法估计的一致，且非差法更具有灵活性，因此利用非差法估计ZTD的应用也越来越广泛[6]。利用非差法估计ZTD又可分为非差网解法和精密单点定位法(precise point positioning，PPP)。对于小区域跟踪网，非差网解法仍然需要引入远距离测站(500～2 000 km)，以获得绝对延迟[7]。PPP法是指利用单站非差观测值估计ZTD，可直接获得绝对延迟，处理大规模数据的速度较快[8-9]。相关研究表明，利用PPP法估计的全球定位系统(global positioning system，GPS)ZTD精度优于6 mm[10]，利用GPS及格洛纳斯卫星导航系统(global navigation satellite system,GLONASS)组合估计的ZTD精度为1 cm左右[11]。

虽然国内外学者在GNSS ZTD估计方面做了大量的研究工作，但针对北斗卫星导航系统(BeiDou navigation satellite system，BDS)ZTD或BDS/GPS组合ZTD估计的研究较少。文献[12]利用中科院测地所计算的精密轨道和钟差估计BDS/GPS组合ZTD，以欧洲定轨中心(center for orbit determination in Europe，CODE)提供的精密轨道和钟差产品估计的GPS ZTD为参考值，得出BDS ZTD的估计精度为2 cm，BDS/GPS组合ZTD的估计精度与GPS相当。文献[13]以国际GNSS服务组织(The International GNSS Service，IGS)提供的精密轨道和钟差估计的GPS ZTD为参考值，分别采用网解法和PPP法估计BDS ZTD，其估计的偏差和标准差分别为2和5 mm[13]。已有研究均是利用自身解算的精密轨道和钟差估计BDS ZTD。

武汉大学(WHU)和德国地学中心(GFZ)在2014-03发布了BDS系统的精密轨道和钟差产品。为评估利用现阶段提供的精密轨道和钟差产品估计BDS/GPS ZTD的效果，本文分别对BDS、GPS、BDS/GPS组合在未固定跟踪站坐标和固定跟踪站坐标情况下估计的ZTD进行研究。

1 BDS/GPS组合PPP法估计ZTD

1.1 BDS/GPS组合估计ZTD的数学模型

在BDS/GPS组合PPP法估计ZTD的过程中，采用双频观测值消除电离层的影响，使用精密轨道和精密钟差来固定卫星轨道和钟差，同时顾及GPS系统和BDS系统之间的时空基准不统一，引入2类接收机钟差。BDS/GPS组合PPP法的观测模型[14]可以表示为

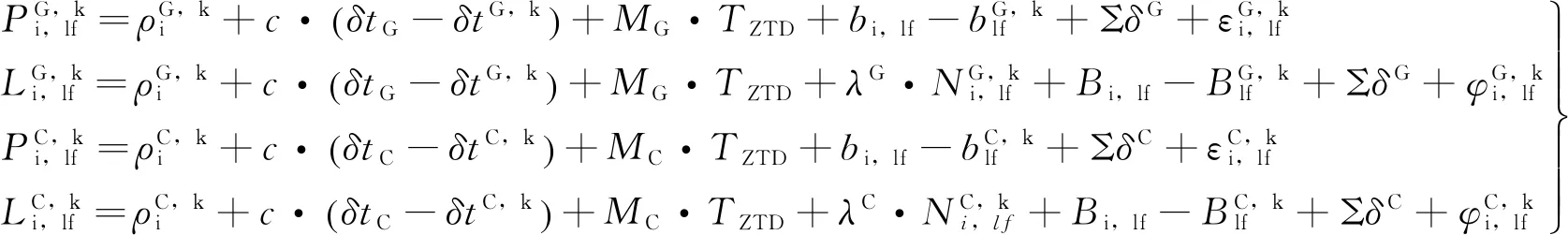
(1)

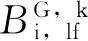
1.2 ZTD参数估计与误差处理

采用WHU提供的精密轨道和钟差产品，ZTD的采样间隔为5 min，伪距先验方差为1 m，相位先验方差0.01个周期，数据处理流程如图1所示。

图1中数据预处理是获得高精度参数估值的关键。本研究采用单站TurboEdit方法进行数据预处理，尽可能发现和修复周跳，剔除异常观测值[15]。TurboEdit方法根据导航卫星频率自动选择阈值，进行周跳探测、粗差剔除以及短弧分析。其中主要包括M-W组合法和电离层残差法等。数据预处理后尽可能考虑多的误差改正项，未能精确模型化的误差通过参数估计吸收。采用双频消电离层组合观测值消除电离层一阶影响；考虑天线相位缠绕改正；接收机噪声为白噪声；模糊度参数对未能精确模型化的误差有补偿作用，所以采用实数解；采用IERS Conventions 2010标准改正地球固体潮偏差、海洋潮以及地球极潮；采用绝对相位模型改正天线相位偏差。

在利用PPP估计ZTD的过程中，采用全球投影函数(global mapping function，GMF)加Saastamoinen模型作为对流层延迟初值，气象数据从全球气压与温度模型(global pressure and temperature model，GPT)获得，剩余残差采用随机游走过程模拟。为了能在最小二乘估计中实现随机过程估计的方法，采用同时估计状态参数和确定性参数的最小二乘递推算法，即：首先把状态方程及状态参数的先验信息转化为相应的等价观测方程；然后在组成法方程的过程中，逐步消去一些状态参数[16]。

2 实验与结果分析

为了评价利用BDS/GPS组合PPP法估计ZTD的效果，采用BDS、GPS和BDS/GPS组合PPP法在未固定跟踪站坐标和固定跟踪站坐标的情况下估计ZTD。实验选取8个多系统实验(multi-GNSS experiment，MGEX)跟踪站2014年年积日第152天至272天(6月至9月)的BDS/GPS观测数据，数据采样间隔为30°。为了评估结果的精度，以IGS提供的对流层产品(简称IGS ZTD)作为参考值，与PPP法估计出的ZTD相比较并统计偏差平均值MEAN和标准差(standard deviation，STD)。

为了分析利用上述策略估计ZTD的效果，以日本的GMSD跟踪站为例，在未固定跟踪站的情况下，使用BDS、GPS和BDS/GPS组合PPP法处理第218天观测数据得到ZTD，如图2所示。

从图中可看出，由GPS或BDS/GPS组合估计的ZTD与IGS ZTD有较好的一致性，且ZTD估值相近，不存在明显的系统性偏差；由BDS估计的ZTD与IGS ZTD变化趋势一致，但在大部分时段存在一定的系统性偏差。

为了进一步分析在未固定跟踪站的情况下采用BDS、GPS和BDS/GPS组合PPP法估计ZTD的效果，统计了8个跟踪站与IGS ZTD的4个月的差值时间序列，并按天统计差值的均值，如图3所示。

由图可知：利用BDS估计的ZTD与IGS ZTD的差值浮动范围为-70 ～ +50 mm，且每个跟踪站与其对应IGS ZTD的差值存在规律性偏差；利用GPS或BDS/GPS组合估计的ZTD与IGS ZTD的差值浮动范围为-10 ～ +10 mm，无明显的规律性偏差。通过长期的观测数据表明，利用BDS估计的ZTD不稳定，波动幅度较大；这主要是受到BDS卫星少和跟踪站可观测卫星的几何构型的影响，中纬度跟踪站(CUT0、GMSD等)的平均可观测卫星数为8颗以上，但主要分布跟踪站在一侧，几何构型差，而其他区域的一些跟踪站(BRST、VILL等)可观测卫星较少，平均可观测卫星数为4～6颗。利用GPS或BDS/GPS组合估计的ZTD随时间变化幅度较小，较稳定。因此，利用BDS/GPS组合估计ZTD可以削弱利用BDS估计ZTD带来的差值波动幅度大的影响。

通常，GNSS跟踪站以及用来观测水汽含量的天文参考站都是固定的，坐标变化微小；因此可以通过固定跟踪站坐标减少参数估计中的未知数。针对选取的8个跟踪站，利用PPP法解算8个跟踪站的GPS数据得到单天解，在估计ZTD的过程中使用解算的GPS单天解固定跟踪站坐标，并给GPS单天解附加一个微小权约束。图4显示了在固定跟踪站坐标后，利用BDS、GPS、GPS/BDS估计的ZTD与IGS ZTD差值时间序列，并按天统计差值的均值。

从图中可看出：固定跟踪站坐标后，利用BDS、GPS、GPS/BDS估计的ZTD与IGS ZTD的差值浮动范围均为-8 ～ +8 mm，这说明固定跟踪站坐标提高了BDS ZTD的稳定性；但固定跟踪站坐标对GPS ZTD和GPS/BDS组合ZTD影响较小，无明显变化。

以IGS ZTD为参考值，表1分别统计了采用BDS、GPS和BDS/GPS组合PPP法在未固定跟踪站坐标和固定跟踪站坐标的情况下估计的ZTD平均偏差MEAN和STD(4个月)。

由表中给出的平均偏差MEAN来看：BDS ZTD在未固定跟踪站坐标情况下的MEAN在23 mm以内，固定坐标后(FBDS)的MEAN在14.2 mm以内；GPS ZTD在未固定跟踪站坐标情况下的MEAN在1.0 mm以内，固定坐标后(FGPS)的MEAN在1.9 mm以内；BDS/GPS组合ZTD在未固定跟踪站坐标情况下的MEAN在3.0 mm以内，固定坐标后(FBDS/GPS)的MEAN在2.5 mm以内。与未固定跟踪站坐标估计的BDS ZTD相比，固定跟踪站站坐标后估计的BDS ZTD的MEAN减小了50 %以上；与未固定跟踪站坐标估计的GPS ZTD或BDS/GPS组合ZTD相比，固定坐标后估计的GPS ZTD或BDS/GPS组合ZTD的MEAN没有减小，这说明使用BDS估计ZTD时固定跟踪站坐标较好；而使用GPS或BDS/GPS组合估计ZTD时无需固定跟踪站坐标。值得注意的是，固定跟踪站后BDS ZTD明显减小，说明BDS的精密定轨和钟差产品的精度需要继续提高。

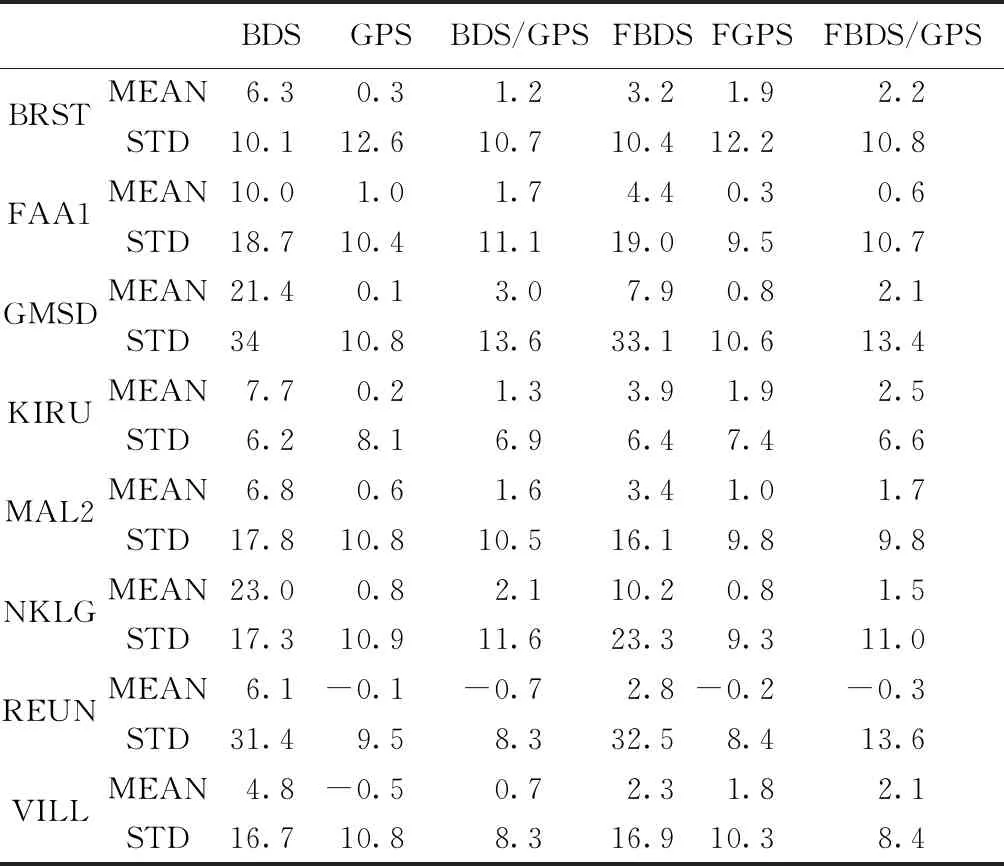
mm

从给出的STD来看，在未固定跟踪站的情况下，BDS ZTD的STD优于34 mm，GPS ZTD的STD优于13 mm，BDS/GPS组合ZTD的STD优于14 mm；在固定跟踪站的情况下，BDS ZTD的STD优于34 mm，GPS ZTD的STD优于13 mm，BDS/GPS组合ZTD的STD优于14 mm。BDS ZTD的STD明显高于GPS ZTD或BDS/GPS组合ZTD的STD，且固定跟踪站坐标对STD几乎没有影响，这是因为二代BDS没有准确的姿态模型和天线相位中心模型，利用BDS估计的ZTD存在系统误差；利用BDS/GPS组合与GPS估计的ZTD精度近乎一致，均在13 mm内，这说明使用BDS/GPS组合与GPS估计的ZTD与IGS产品符合得比较好。与GPS ZTD相比，虽然BDS/GPS组合估计的ZTD没有获得较高的精度，但BDS/GPS组合观测增加了可视卫星数，这对观测条件恶劣的地方，比如城市、山区，具有重要的意义。另外，比较固定跟踪站坐标估计的BDS ZTD和未固定跟踪站坐标估计的BDS/GPS组合ZTD发现，虽然二者MEAN的互差仅为几个mm，但RMS互差为1～2 cm；由此可见，利用BDS/GPS组合估计ZTD的方式优于在固定跟踪站坐标后利用BDS估计ZTD的方式。值得说明的是，这6种方法估计的ZTD与IGS ZTD差值的STD均超过了6.4 mm，这种差异主要是因为利用PPP法估计ZTD过程中具体的数据处理策略不一致，如参数设置、投影函数等。

3 结束语

为分析利用BDS/GPS组合PPP法估计ZTD的效果，采用武汉大学提供的精密轨道和钟差产品，对8个MEGX跟踪站2014年6月至9月的数据进行了测试分析，系统比较了采用BDS、GPS和BDS/GPS组合PPP法在未固定跟踪站坐标和固定跟踪站坐标情况下估计ZTD的效果。结果表明，利用PPP法估计ZTD，BDS ZTD现阶段的STD优于34 mm，GPS ZTD现阶段的STD优于13 mm，BDS/GPS组合ZTD现阶段的STD优于14 mm。与利用GPS估计ZTD的方式相比，利用BDS/GPS组合估计ZTD的STD与GPS相当。另外，通过固定跟踪站坐标的方式虽然可以提高利用BDS估计ZTD的稳定性，但是不能提高精度。

致谢：感谢IGS分析中心、武汉大学卫星分析中心为本文提供了丰富的实验数据和相关产品。

[1] 曹云昌，方宗义，夏青.轨道误差对近实时 GPS遥感水汽的影响研究[J].气象科技，2004，32(4)：229-232.

[2] SHI J，XU C，GUO J，et al.Real-time GPS precise point positioning-based precipitable water vapor estimation for rainfall monitoring and forecasting[J].IEEE Transactions on Geoscience and Remote Sensing，2015，53(6)：3452-3459.

[3] 盛峥，黄思训，张流青，等.利用 GPS 技术探测大气中的水汽含量[J].沈阳师范大学学报(自然科学版)，2005，23(1)：33-37.

[4] 李征航.GPS测量与数据处理[M].武汉：武汉大学出版社，2010：107-113.

[5] 毕研盟，毛节泰，杨光林，等.地基GPS遥感观测安徽地区水汽特征[J].气象科技，2004，32(4)：225-228.

[6] CHEN J，ZHANG Y，WANG J，et al.A simplified and unified model of multi-GNSS precise point positioning[J].Advances in Space Research，2015，55(1)：125-134.

[7] GE M，CHEN J，DOUSA J，et al.A computationally efficient approach for estimating high-rate satellite clock corrections in realtime[J].GPS Solutions，2012，16(1)：9-17.

[8] DUAN J，BEVIS M，FANG P，et al.GPS meteorology：direct estimation of the absolute value of precipitable water[J].Journal of Applied Meteorology，1996，35(6)：830-838.

[9] 叶世榕，张双成，刘经南.精密单点定位方法估计对流层延迟精度分析[J].武汉大学学报(信息科学版)，2008，33(8)：788-791.

[10]何锡扬，张小红，李星星，等.PPP 估计天顶对流层延迟方法与结果分析[J].测绘信息与工程，2010 (1)：3-5.

[11]蔡昌盛，夏朋飞，史俊波，等.利用 GPS/GLONASS 组合精密单点定位方法估计天顶对流层延迟[J].大地测量与地球动力学，2013，33(2)：54-57.

[12]范磊，钟世明，潭冰峰，等.基于BDS与GPS精密单点定位的天顶对流层延迟估计比较[J].大地测量与地球动力学，2015，01：67-71.

[13]XU A，XU Z，GE M，et al.Estimating zenith tropospheric delays from BeiDou navigation satellite system observations[J].Sensors，2013，13(4)：4514-4526.

[14]李星星.GNSS精密单点定位及非差模糊度快速确定方法研究[D].武汉：武汉大学，2013：58-69.

[15]BLEWITT G.Jet Propulsion Laboratory，California Institute of Technology，Pasadena[J].Geophysical Research Letters，1990，17(3)：199-202.

[16]葛茂荣，刘经南.GPS定位中对流层折射估计研究[J].测绘学报，1996，25(4)：285-291.

Analysis on performance of estimating zenith tropospheric delays for combined BDS/GPS

TANGLongjiang1，XUAigong1，XUZongqiu1，2，LILei1

(1.School of Geomatics, Liaoning Technical University，Fuxin，Liaoning 123000，China；2.Research Center of GNSS，Wuhan University，Wuhan 430079，China)

In order to further analyze the accuracy of BDS/GPS ZTD，the paper selected the data of 8 MGEX stations during the period of June to September 2014，used PPP to estimate BDS ZTD，GPS ZTD and BDS/GPS ZTD under the conditions of fixed and unfixed station coordinates respectively，and analytically compared with the tropospheric products of IGS.Experimental result showed that currently the standard deviation of BDS ZTD could be better than 34 mm，and that of GPS ZTD would be similar with combined BDS/GPS on 14 mm or better；moreover， compared with BDS ZTD under the unfixed MEGX station，the way of fixed station could improve the estimation stability of BDS ZTD，but not the accuracy.

combined BDS/GPS；zenith tropospheric delays；precise point positioning；tropospheric products of IGS

2016-08-01

国家863计划项目(2014AA121301)；国家青年基金项目(41504030，41504010)；辽宁省教育厅科学研究一般项目(L2014139)；辽宁省科技厅博士启动基金项目(201501126)。

唐龙江(1991—)，男，江苏盐城人，硕士研究生，研究方向为GNSS精密定位及数据处理。

徐爱功(1963—)，男，教授，博士生导师，研究方向为全球卫星定位系统与地理信息系统集成及其在智能交通系统中的应用研究。

唐龙江，徐爱功，徐宗秋，等.BDS/GPS组合天顶对流层延迟估计的精度分析[J].导航定位学报，2017，5(3)：52-56.(TANG Longjiang，XU Aigong，XU Zongqiu，et al.Analysis on performance of estimating zenith tropospheric delays for combined BDS/GPS[J].Journal of Navigation and Positioning，2017，5(3)：52-56.)

10.16547/j.cnki.10-1096.20170311.

P228

A

2095-4999(2017)03-0052-05