灰色神经网络在GPS高程拟合中的应用

杨 帆，王小兵,2，谢洋洋，李 宁，滑东飞

(1.辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2.南通市测绘院有限公司，江苏 南通 226000)

灰色神经网络在GPS高程拟合中的应用

杨 帆1，王小兵1,2，谢洋洋1，李 宁1，滑东飞1

(1.辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2.南通市测绘院有限公司，江苏 南通 226000)

针对传统单一GPS高程拟合方法存在对数据和测区要求较高的问题，提出一种改进的灰色神经网络拟合方法：通过添加跳脱系数修正适应度函数扩大搜索范围，对果蝇优化算法进行改进，有效地提高算法的寻优能力；利用改进的果蝇算法优化灰色神经网络参数，训练灰色神经网络模型获得模型最佳参数，完成对GPS高程的拟合。实验结果表明该方法具有较高的拟合精度和较强的鲁棒性。

GPS高程拟合；果蝇优化算法；灰色神经网络；拟合精度；鲁棒性

0 引言

全球定位系统(global positioning system，GPS)技术因其全天候、高精度和自动测量的特点，已经在工程领域拥有广泛的应用。利用GPS测量技术可以直接测定地面点的大地高，然而大地高不具有物理意义，实际生产中普遍使用的是与地球重力场密切相关的正常高[1]。GPS测定出的基于参考椭球面的大地高与基于似大地水准面的正常高的差距称为高程异常，如何精确地拟合出高程异常，将大地高系统转化为工程直接应用的正常高系统具有实际的意义。目前，已经有许多专家学者投入到GPS高程系统转换的的研究中，提出了多种方法确定高程异常；但这些求算方法都存在种种缺陷和不足。几何分析法建立在大量的样本数据基础上，对测试样本要求较高[2]；地球重力场模型法需要大量高精度的重力测量资料，但实际工作中很难达到所需要求[3]；二次多项式曲面法适合于地势平坦和面积比较小的测区，对于大面积和地势起伏较大的测区往往精度不高，无法满足工程需求[4]。灰色神经网络模型(grey neutral networks model，GNNM)是由灰色模型和神经网络模型有机融合而成，继承了2种模型的优点，弥补了单一预报模型使用中的不足[5]。灰色神经网络凭借着建模简单、易于计算机语言实现，以及良好的数据处理能力和预测效果在工程领域有着广泛的应用[6-7]。

本文提出灰色神经网络模型的GPS拟合方法，并使用改进型果蝇优化算法(fruit fly optimization algorithm，FOA)对模型参数进行优化来建立GPS高程拟合模型。

1 灰色神经网络模型

设非确定系统的特征值原始数列

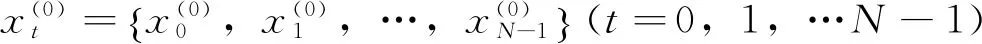
(1)

经过一次累加后得到的行矩阵

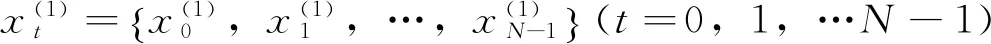
(2)

灰色神经网络模型(grey neural network model，GNNM)的微分方程式为

(3)

式中：y1为系统输出参数；yn(n=2，3，…，n)为系统输入参数；a、b1、b2、 …、bn为微分方程系数。微分方程解的表达式为

(4)

转化式(4)得

(5)

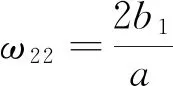
θ=(1+e-at)(d-y1(0))。

(6)

2 改进型果蝇优化算法

2.1 果蝇优化算法

FOA是基于果蝇觅食行为过程推演出全局寻优的演化算法。果蝇凭借着良好的嗅觉能力能够快速捕捉到空气中弥漫的食物气息判断食物源的方向。逼近食物源后他们依靠着敏锐的视觉能力迅速发现食物和同伴并朝那个方向飞去继而寻找到食物[8-10]。

2.2 改进型果蝇优化算法

FOA算法由于适应度函数问题导致算法容易早熟收敛而无法取得。添加跳脱系数Δ修正适应度函数，改进后的表达式[11]为

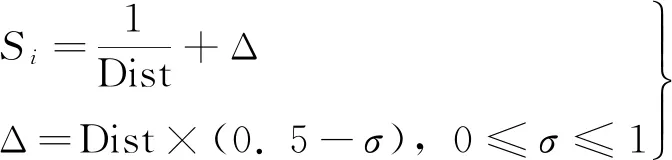
(7)

式中：Dist为果蝇个体左边(X，Y，Z)至坐标原点的距离；σ为0至1之间任意值。

此外原始的果蝇算法是在二维空间寻找全局最优值，本文引入三维空间的概念，图2为果蝇群体三维空间搜寻食物的示意图。

改进的FOA优化GNNM过程分为以下步骤：

1)初始化果蝇群体的位置(Xaxis，Yaxis，Zaxis)、种群数量、迭代次数。

2)赋予果蝇个体利用嗅觉搜索食物的随机方向和距离，randvalue为[-10，10]区间内任意值，则可得

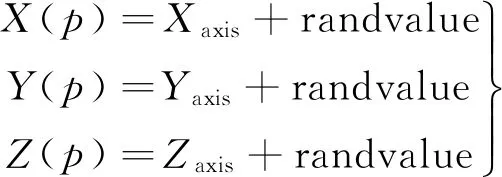
(8)

3)由于无法获知食物的具体位置，因此先估计果蝇个体位置(X，Y，Z)与原点的距离，再计算味道浓度判定函数值为

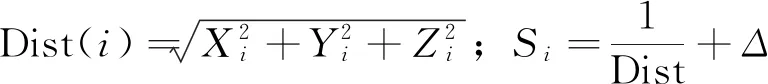
(9)

4)利用味道浓度判定函数求算果蝇个体的味道浓度为

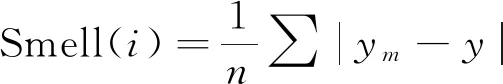
(10)

式中：ym为预测值；y为目标值。

5)找出有最佳气味浓度(bestSmell)的位置(bestindex)上的单个果蝇，即

[bestSmell bestindex]=min(Smell)。

(11)

6)保留最佳味道浓度值初始位置(X(bestindex)，Y(bestindex)，Z(bestindex))和初始味道浓度S(bestindex)，果蝇利用视觉向此位置飞去，

(12)

7)优化迭代和重复步骤2)至5)，判断是否优于前一次迭代味道浓度，如果是则执行步骤6)，否则返回，直到达到最大数量的迭代，将保留的最佳参数代入模型进行预测获得预测结果。

3 实验与结果分析

本文选取沿江某区域40组经过四等水准联测的GPS水准高程点作为实验样本，其中30组均匀分布于测区的水准高程点作为学习集，其余10组作为测试集用来检测模型的拟合精度，图3为实验样本分布图。实验将GPS的高程点X、Y坐标作为拟合模型的输入向量，高程异常作为模型输出向量，并利用线性变换最大最小法对实验样本数据进行归一化处理，把样本数据都转化至[0，1]之间。

样本数据变换函数表达式[12]为

(13)

式中：yk为经过线性变化后的值；ymax为数据最大值；ymin为数据最小值。对MFOA进行参数设定：随机初始化果蝇群体位置为[0，1]；果蝇个体飞行方向与飞行距离为[-10，10]；果蝇种群规模为20；迭代次数为100。采用改进型果蝇优化算法对灰色神经网络参数(a，b1，b2)进行优化建立预测模型，网络参数经过100次动态迭代寻优均方差的收敛情况和搜索路径如图4、图5所示。图4中改进型果蝇优化算法经过16次迭代开始收敛，收敛误差为0.336 mm，获得的网络参数为a=9.906 4，b1=9.902 6，b2=9.903 1。将最佳的模型参数代入灰色神经网络进行训练。

表1为不同拟合方法的精度比较，从高程异常拟合残差进行对比分析。

从表中可知：GNNM最大高程异常拟合残差达到4.5 cm，最小为-0.13 cm，整体起伏比较大。主要是由于网络模型参数的随机性造成拟合效果不是理想；采用与改进的FOA-GNNM相同实验参数的FOA-GNNM最大高程异常拟合残差为3.09 cm，最小为0.033 cm，高程拟合效果优于GNNM，但差于改进的FOA-GNNM，主要是因为FOA算法早熟收敛，优化的网络参数不是全局最佳；改进的FOA-GNNM模型避免模型参数陷入局部最优，所以GPS高程拟合效果最好，并且最大、最小高程拟合残差分别为0.7和0.1 cm，即所有高程异常拟合残差均在1 cm以下，符合高程拟合要求，整体稳定性较好。从外符合精度分析，改进的FOA-GNNM外符合精度为0.5 cm，远远小于FOA-GNNM和GNNM，说明改进的FOA-GNNM方法具有良好的高程拟合精度。

图6为3种拟合方法的残差对比。

表1 不同拟合方法精度比较

图中可以看出，改进的FOA-GNNM变化比较平稳，而FOA-GNNM和GNNM残差波动性比较大，说明改进的FOA-GNNM具有较好的鲁棒性。综上所述，改进的FOA-GNNM模型凭借其良好的GPS高程拟合精度和稳定性等优点，能够较好地对GPS高程进行拟合。

4 结束语

改进的FOA是在原算法的基础上增加一个跳脱参数避免陷入局部极值，此外搜索范围由二维拓展至三维空间，有效提高了收敛速度，降低了收敛误差。将改进果蝇优化算法优化灰色神经网络建立GPS高程拟合模型，并应用实际样本数据进行验证，仿真实验表明此方法具有较高的拟合精度和较强的泛化能力，能够为GPS高程拟合的相关研究提供参考。

[1] 马腾.BP神经网络在GPS高程拟合中的应用[D]. 呼和浩特：内蒙古农业大学，2008：1-3.

[2] 任超，吴伟，黄征凯，等.基于AIC准则的RBF神经网络在GPS高程拟合中的应用[J]. 测绘科学，2013，38(2)：77-79.

[3] 张昊，王琪洁，朱建军，等.样本数据预处理对基于BP神经网络的GPS高程拟合的影响[J]. 大地测量与地球动力学，2011，31(2)：125-128.

[4] 高宁，高彩云，徐长海.补偿最小二乘估计在确定高程异常中的应用[J]. 测绘科学，2011，36(1):35-37.

[5] 李小燕.灰色神经网络预测模型的优化研究[D].武汉：武汉理工大学，2009：6-9.

[6] 雷斌，陶海龙，徐晓光.基于改进粒子群优化算法的灰色神经网络的铁路货运量预测[J]. 计算机应用，2012，32(10):2948-2951.

[7] 邹兵，陈西宏，薛伦生，等.果蝇优化算法优化灰色神经网络的卫星钟差预报[J]. 测绘科学，2014，39(9)：44-48.

[8] 张宏伟，朱志洁，霍丙杰，等.基于改进的FOA-SVM导水裂隙带高度预测研究[J]. 中国安全科学学报，2013，23(10)：9-14.

[9] 潘文超.果蝇最佳化演算法[M].台北：沧海书局，2013：1-3.

[10]PAN W.Using modified fruit fly optimization algorithm to perform the function test and case studies[J]. Connection Science，2013，25(2/3)： 151-160.

[11]ISCAN H，GUNDUZ M.A survey on fruit fly optimization algorithm[C]//The Institute of Electrical and Electronic Engineers(IEEE).Proceedings of the 11th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS).Bangkok，Thailand：IEEE，2015：520-527.

[12]王小川.MATLAB神经网络43个案例分析[M]. 北京：北京航空航天大学出版社，2013：4-5.

Application of grey neural network in GPS height fitting

YANGFan1，WANGXiaobing1，2，XIEYangyang1，LINing1，HUADongfei1

(1.School of Geomatics，Liaoning Technical University，Fuxin，Liaoning 123000，China；2.Nantong Surveying &Mapping Institute Co.，Ltd，Nantong，Jiangsu 226006，China)

Aiming at the problem that the traditional single GPS height fitting method requires more demanding data and surveying area，the paper proposed an improved fitting grey neural network：function fitness was modified by adding the jump coefficients，and the algorithm of fruit fly was extended to improve the searching range，which could enhance the searching ability of the algorithm；the improved algorithm was used to optimize the parameters of grey neural network，and the optimal value was obtained by training the grey neural network model to fit the GPS height.Experimental result showed that the proposed method could have higher fitting accuracy and stronger robustness.

GPS height fitting；fruit fly optimization algorithm；grey neural network；fitting accuracy；robustness

2016-10-19

国家自然科学基金项目(50604009)；辽宁省“百千万人才工程”人选资助项目(2010921099)。

杨帆(1972—)，男，湖北随州人，博士，教授，研究方向为研究生教育管理、变形监测与预报。

王小兵(1987—)，男，江苏泰州人，硕士研究生，研究方向为变形监测与预报、变形监测数据处理。

杨帆，王小兵，谢洋洋，等.灰色神经网络在GPS高程拟合中的应用[J].导航定位学报，2017，5(3):90-93,100.(YANG Fan，WANG Xiaobing，XIE Yangyang，et al.Application of grey neural network in GPS height fitting[J].Journal of Navigation and Positioning，2017，5(3):90-93,100.)

10.16547/j.cnki.10-1096.20170318.

P228

A

2095-4999(2017)03-0090-05