改进LAMBDA算法的双频BDS整周模糊度快速固定

龚宵雪，徐爱功，祝会忠，李 博，马天明，高 猛

(辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000)

改进LAMBDA算法的双频BDS整周模糊度快速固定

龚宵雪，徐爱功，祝会忠，李 博，马天明，高 猛

(辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000)

针对双频BDS短基线解算法方程病态严重，模糊度的浮点解精度低，导致LAMBDA算法搜索范围过大、搜索时间过长等问题，提出一种改进的LAMBDA算法：运用Tikhonov正则化理论构造一种具有明确物理意义的正则化矩阵R，以获得精确的整周模糊度浮点解；同时用均方误差矩阵RMSEM代替原算法的协方差阵确定模糊度的搜索范围，缩短初始化时间，提高搜索效率。实验结果表明：改进后的LAMBDA算法获得的模糊度浮点解精度显著提高，且无需初始化时间，能够正确固定模糊度的整数解，快速实现cm级定位。

BDS；整周模糊度；LAMBDA算法；正则化；浮点解

0 引言

北斗卫星导航系统(Beidou navigation satellite system，BDS)是我国具有独立自主产权、自主研发的卫星导航定位系统[1]。2012-12-27，BDS空间信号接口控制文件正式版1.0正式公布，BDS已开始向中国及亚太大部分地区正式提供无源定位、导航、授时服务[2]。截至2016-06-13，BDS在轨卫星共计23颗，其中7颗地球静止轨道(geostationary Earth orbit，GEO)卫星、8颗倾斜地球同步轨道(inclined geo-synchronous orbits，IGSO)卫星及8颗中圆地球轨道(medium Earth orbit，MEO)卫星的定位精度为10 m、测速精度为0.2 m/s、授时精度为10 ns[3]。到2020年左右将全面建成BDS，形成全球服务能力。

BDS现在也已经加入到高精度定位中。在高精度定位中，通常用载波相位差分技术进行快速定位，而载波相位整周模糊度的准确固定是BDS定位的核心问题[4-5]，整周模糊度一旦确定，相位观测值即转变为准确的距离观测值[6]。关于如何更好地确定模糊度，已有许多学者提出了很多方法。文献[7]针对病态法矩阵，提出基于Tikhonov正则化原理的一种选择正则化矩阵R的新方法，减弱了法方程的病态性，但没有明确R的物理意义；文献[8]将直接算法(direct calculation，DC)推广为直接解算短基线全球定位系统(global positioning system，GPS)整周模糊度，但DC算法需要保证基线长度的精度优于0.7 m；文献[9]利用单历元测码伪距观测值和双频载波相位观测值组成双差观测方程，解算L1/L2双差整周模糊度时具有较高的效率和成功率，利用方差对模糊度进行分组降维处理，缩小了模糊度搜索空间；文献[10]指出模糊度去相关处理(Z变换)有迭代法和联合去相关法2种算法，通过比较2种方法的条件数和去相关数，得出联合去相关法的效果略高于迭代法，在整周模糊度搜索前对原始模糊度进行降相关处理，使搜索椭球更接近球体，提高了搜索效率，但未对模糊度浮点解精度做出说明；文献[11]提出了一种利用多频观测值，基于有几何模型的逐级模糊度固定方法，先通过伪距固定超宽巷模糊度，然后用无模糊度的超宽巷约束2个宽巷模糊度求解，最后使用无模糊度的宽巷观测值约束窄巷模糊度求解，其模糊度固定达到100 %的成功率。

对于如何快速又精确地固定模糊度的问题，本文通过运用Tikhonov正则化的理论，构造出一种具有明确物理意义的正则化矩阵R，使LAMBDA算法得到改进，以解决法方程的病态性，获得精确的整周模糊度浮点解；同时用均方误差矩阵(mean square error matrix，MSEM)RMSEM代替原算法的协方差阵确定模糊度的搜索范围，缩短初始化时间，提高搜索效率。

1 LAMBDA算法原理

LAMBDA算法的核心问题就是整周模糊度最小二乘估计，主要分为2个组成部分：整数变换和基于乔里斯基分解(LTDL)的整周搜索。整数最小二乘估计的基本方法为

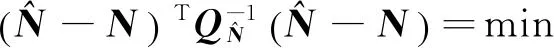
(1)

1.1 整数变换

(2)

(3)

1.2 整周搜索

(4)

求得最优的整数组合z之后，再进行逆变换，即

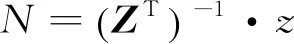
(5)

式中Z为整数变换矩阵。变换后的参数N满足式(1)，也就是说，逆变换后得到的参数N就是要寻求的最佳整数模糊度向量。

在LAMBDA法中，是通过LTDL分解对协因数阵QX进行整数变换来提高搜索效率的，其中L为下三角矩阵，D为对角阵。

2 基线解算的一般LAMBDA算法

LAMBDA算法主要是对载波相位双差观测方程中的模糊度进行搜索解算，在短基线数据处理时，双差可以消除卫星钟差和接收机钟差，同时也大幅度削弱了卫星轨道误差、电离层延迟和对流层延迟等误差。将BDS的B1、B2双差载波相位观测值组成宽巷载波相位观测值，由于B1、B2载波相位宽巷观测值的波长达84.7 cm，因而很容易准确确定其整周模糊度，然后解算载波相位观测值的整周模糊度[13]。

设2台接收机在某历元可共同观测k+1颗卫星，则可组成k个相位双差观测方程，其线性化后的双差观测方程[14]简写为

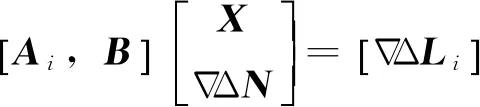
(6)

若2台GPS接收机连续观测n1个历元，则总的双差观测方程为

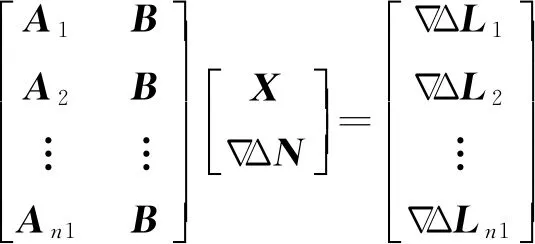
(7)

可以将式(7)简写成

(8)

根据最小二乘(least square method，LS)原则，由式(8)组成法方程，得到LS解为

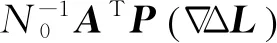
(9)

式中N0=ATPA， 为LS估计的法矩阵。Y的协因数阵为

(10)

在定位过程中，如果观测历元数n1较少时，法矩阵N0的条件数一般在106以上，法方程病态严重，模糊度的浮点解精度低，导致LAMBDA算法搜索范围过大、搜索时间过长，甚至不能正确固定整周模糊度。为了弥补LAMBDA算法的不足，本文对LAMBDA算法进行改进，使整周模糊度可以快速、高效地固定。

3 改进的LAMBDA算法

根据Tikhonov正则化原理，求解式(8)采用的估计准则[7]为

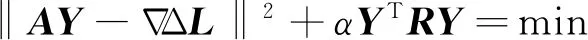
(11)

式中：α是平滑因子或正则化参数；R是正则化矩阵，用于减弱法方程病态；Ω(Y)是稳定泛函；‖•‖表示欧氏2-范数。

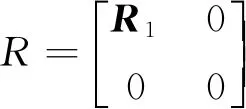
(12)

式中：R是奇异矩阵；R1是基线分量部分的先验协因数阵的逆阵。系数1/100 000是根据待定点近似坐标偏差与相位观测值精度比选取的。

构造正则化矩阵R后，应用L曲线法进行了大量的实际计算，其计算结果表明选取正则化参数α=1时效果最好。则式(11)变为

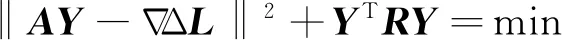
(13)

结合式(8)，由估计准则求导组成法方程为

(14)

式中R为正则化矩阵。解算式(14)的法方程，得

(15)

相应的均方误差矩阵RMSEM近似[14]取为

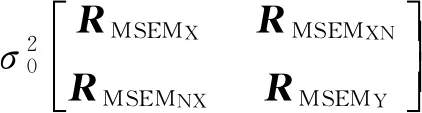
(16)

式中σ0为单位权中误差。

4 实验及结果分析

为了验证改进后的LAMBDA算法的效果[15]，采用BDS/GPS双系统双频接收机对长度为50 m的基线进行了40 min的数据采集，采样间隔为1 s，卫星截止高度角为15°。实验对基线数据按照以下2种方案进行解算：1)传统的一般算法固定整周模糊度；2)通过正则化改进的LAMBDA算法固定整周模糊度。

本文利用Ratio值作为模糊度得到固定解的置信度指标，Ratio值是由次优的模糊度向量的残差平方和与最优的模糊度向量的残差平方和的比值计算得到的。本文取Ratio值为2，当Ratio值大于2时，认为模糊度固定正确。利用改进前和改进后2种LAMBDA算法固定整周模糊度的Ratio值，其结果如图1所示。

由图1可知，改进后Ratio值小于2的个数远远少于改进前的个数。改进后只有1个历元Ratio值小于2，改进前有498个历元Ratio值小于2；所以利用改进后的LAMBDA算法固定的整周模糊度是可靠的。

以1号卫星和2号卫星为例，按照2种算法确定的整周模糊度的浮点解的对比结果如图2所示。因为改进后的LAMBDA算法提高了模糊度浮点解精度，缩小了LAMBDA算法的搜索范围和搜索时间，使模糊度的固定成功率得到提高；所以在得到模糊度固定解之前，提高模糊度浮点解非常有必要。

由图2可知，1号卫星改进前的LAMBDA算法需要大约200个历元才能确定模糊度浮点解，而改进后的LAMBDA算法第1个历元就可以把模糊度浮点解确定；2号卫星在改进算法前也是大约需要200个历元才能确定浮点解，同样改进后的算法在第1个历元就能确定浮点解。可以得出，改进后的LAMBDA算法明显提高了模糊度浮点解的精度，使模糊度的固定成功率得到提高。

仍以1号和2号卫星为例，给出LAMBDA算法改进前后模糊度固定的结果，如图3所示。

由图3可知，改进前的LAMBDA算法的模糊度浮点解在开始时偏差大，所以整数解没有正确固定，经过大约200个历元以后才能固定整数解，而改进后的LAMBDA算法从第1个历元开始就能固定到正确的整数解。

下面对改进前和改进后的LAMBDA算法初始化时间和模糊度固定个数进行统计，结果如表1所示。

表1 初始化时间和模糊度固定个数

根据表1的统计结果可以看出：改进前的LAMBDA算法固定了2 208个历元，而改进后的LAMBDA算法固定了2 399个历元，100 %固定。

在模糊度固定之后，用改进前和改进后的算法解算高精度定位结果，与测站的精确定位结果进行比较，得到东(E)、北(N)、天顶(U)3个方向上的偏差值，如图4所示。

根据图4定位结果，再结合前面的Ratio值、模糊度浮点解和固定解的结果可以看出，改进前的LAMBDA算法需要192个历元才能达到cm级定位精度，而改进后的LAMBDA算法从第1个历元开始就能达到cm级定位，且坐标偏差值变化范围在3 cm之内，与整体解算的结果相比较波动不大，说明改进后LAMBDA算法解的精度更好，定位效率更高。

5 结束语

本文研究了双频BDS短基线解算问题，首先利用宽巷确定其整周模糊度，然后解算载波相位观测值的整周模糊度。针对法方程病态严重，模糊度的浮动解精度低，导致LAMBDA算法搜索范围过大、搜索时间过长问题，运用Tikhonov正则化的理论，构造了一种具有明确物理意义的正则化矩阵R，使LAMBDA算法得到改进，从而获得精确的整周模糊度浮点解，同时用RMSEM代替原算法的协方差阵确定模糊度的搜索范围，提高搜索效率。改进后的LAMBDA算法所获得的模糊度浮点解精度显著提高，可以无需初始化时间，100 %正确固定模糊度的整数解，快速实现cm级定位。

[1] 杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报，2010，39(1)：1-6.

[2] 高猛，徐爱功，祝会忠.双导航定位系统伪距单点定位数据处理方法与精度分析[J].导航定位学报，2014，2(2)：83-88.

[3] 施闯，赵齐乐，李敏，等.北斗卫星导航系统的精密定轨与定位研究[J].中国科学：地球科学，2012，42(6)：854-861.

[4] 卢立果，刘万科，李江卫.降相关对模糊度解算中搜索效率的影响分析[J].测绘学报，2015，44(5)：481-487.

[5] 李豹，许江宁，曹可劲，等.改进LAMBDA算法实现单频GPS整周模糊度快速解算[J].中国惯性技术学报，2013，21(3)：365-368.

[6] 魏子卿，葛茂荣.GPS相对定位的数学模型[M].北京：测绘出版社，1988：105.

[7] 王振杰，欧吉坤，柳林涛.单频GPS快速定位中病态问题的解法研究[J].测绘学报，2005，34(3)：196-201.

[8] 邱蕾，花向红，蔡华，等.GPS短基线整周模糊度的直接解法[J].武汉大学学报(信息科学版)，2009，34(1)：97-99，104.

[9] 祝会忠，高星伟，秘金钟，等.一种GPS整周模糊度单历元解算方法[J].测绘科学，2011，36(4)：9-11.

[10]刘锋，兰孝奇，陈飞.基于LAMBDA整周模糊度解算方法中的整周Z变换算法[J].测绘与空间地理信息，2014，37(4)：51-53.

[11]刘炎炎，叶世榕，江鹏，等.基于北斗三频的短基线单历元模糊度固定[J].武汉大学学报(信息科学版)，2015，40(2)：209-213.

[12]李征航，黄劲松.GPS测量与数据处理[M].武汉：武汉大学出版社，2012：155-158.

[13]祝会忠，徐爱功，高猛.北斗系统载波相位动态差分定位方法[J].测绘科学，2015，40(9)：9-13.

[14]卢秀山，王振杰，欧吉坤，等.单频GPS短基线快速定位中的少数历元算法[J].武汉大学学报(信息科学版)，2007，32(12)：1147-1151.

[15]史仲，吴任洪，王以磊.提高GPS基线解算质量的方法研究[J].测绘通报，2015(4)：69-71.

Rapid resolution of dual frequency BDS integer ambiguity by improved LAMBDA algorithm

GONGXiaoxue，XUAigong，ZHUHuizhong，LIBo，MATianming，GAOMeng

(School of Geomatics，Liaoning Technical University，Fuxin，Liaoning 123000，China)

Aiming at the problem that the solution algorithm of the BDS dual frequency short baseline has ill conditioned equation，and the floating point solution of ambiguity has low precision，leading to the large searching scope and long searching time in using LAMBDA algorithm，the paper proposed an improved LAMBDA algorithm：Tikhonov regularization theory was used to construct a regularized matrixRwith a clear physical meaning for obtaining the accurate floating point solution of integer ambiguity；meanwhile a mean square error matrixRMSEMwas used to replace the covariance matrix of the original algorithm in order to determine the searching range of ambiguity，thus the initialization time was reduced and the searching efficiency was improved.Experimental result showed that by the proposed method，the precision of the floating point solution of ambiguity could be increased significantly without initialization time，the integer ambiguity could be fixed correctly and the positioning with the centimeter level accuracy could be rapidly realized.

BDS；integer ambiguity；LAMBDA algorithm；regularization；floating point solution

2016-10-18

国家重点研发计划项目(2016YFC0803102)；辽宁省高等学校创新团队项目(LT2015013)。

龚宵雪(1991—)，女，河南安阳人，硕士研究生，研究方向为GNSS高精度定位。

龚宵雪，徐爱功，祝会忠，等.改进LAMBDA算法的双频BDS整周模糊度快速固定[J].导航定位学报，2017，5(3)：72-76,83.(GONG Xiaoxue，XU Aigong，ZHU Huizhong，et al.Rapid resolution of dual frequency BDS integer ambiguity by improved LAMBDA algorithm[J].Journal of Navigation and Positioning，2017，5(3)：72-76,83.)

10.16547/j.cnki.10-1096.20170315.

P228

A

2095-4999(2017)03-0072-06