一种MEMS陀螺随机误差的灰色RBF神经网络建模方法

孙 伟，刘得朋，文 剑，吴增林

(辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000)

一种MEMS陀螺随机误差的灰色RBF神经网络建模方法

孙 伟，刘得朋，文 剑，吴增林

(辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000)

为了提高MEMS陀螺仪的精度，利用基于灰色累加累减操作能够减小MEMS陀螺仪随机性的特点，提出一种将灰色理论与径向基函数(RBF)神经网络相结合的MEMS陀螺随机误差建模补偿方案：采用Allan方差分析法对MEMS陀螺输出数据构成的样本空间进行处理并辨识信号中的随机误差项；通过灰色累加累减过程与RBF神经网络的嵌入式耦合，实现MEMS陀螺随机误差预测模型的建立。实验结果表明，与MEMS陀螺实测数据比对后可发现灰色RBF神经网络方法能够有效预测多种随机误差，可进一步提高MEMS陀螺仪输出的预测精度。

MEMS陀螺；灰色模型；RBF神经网络；随机误差

0 引言

微机电系统(micro-electro-mechanical system，MEMS)的陀螺输出信号信噪比低成为制约其精度的主要因素。陀螺仪的随机误差通常包括角度随机游走、量化噪声、零偏不稳定性等误差项[1-3]，如何有效辨识随机误差的成分并补偿，对扩展MEMS惯导系统的应用范围具有十分重要的意义。传统MEMS陀螺仪随机误差建模需进行大量的数据预处理，满足建模要求后方可进行模式定阶及参数估计，存在结构复杂、运算量大、模型精度低等问题。径向基函数(radial basis function，RBF)神经网络技术具有非线性、自适应和自学习等特点[4-7]，能够以任意精度逼近任意非线性映射，本质上适用于MEMS陀螺的随机过程建模；然而在运用神经网络建模过程中发现，模型精度易受数据随机性影响：为提高建模精度，需对模型作进一步改进。灰色理论通过灰色累加灰色累减过程可在很大程度上减弱陀螺输出的随机性，将二者结合能够建立高效的随机漂移补偿模型。

本文研究陀螺输出信号的预处理，针对MEMS陀螺输出的随机漂移特点，并根据MEMS陀螺输出信号的Allan方差分析结果，将灰色理论与神经网络相结合并对陀螺漂移数据进行建模与补偿。

1 MEMS陀螺随机误差辨识

Allan方差最初是用于分析振荡器的相位和频率不稳定性，由于MEMS陀螺本身也具有振荡器的特征，因此该方法随后被广泛应用于各种惯性传感器的随机误差辨识中[8-10]。通过对MEMS陀螺输出数据构成的一个样本空间进行处理，辨识出信号中的随机误差项及其贡献。Allan方差计算步骤如下：

设t0为陀螺随机数据采样时间，N为采样点总和。将获得N个采样点划分为K组，每组采样点记为M=N/K(M≤(N-1)/2)， 每组所用时间t=t0M定义为相关时间，得到K组中每组陀螺输出的平均值为

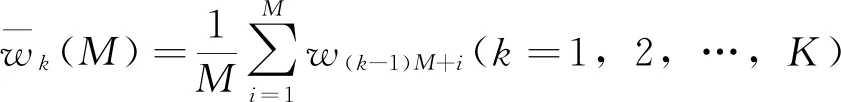
(1)

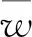
Allan方差定义为

(2)

表1 陀螺随机噪声与Allan方差对应关系

注：Q表示量化噪声系数；R表示速率斜坡系数；B表示偏差不稳定性系数。

将实验室现有MEMS传感器固定在三轴转台后预热1 h。以采样频率100 Hz采集静止时MEMS陀螺仪三轴输出，绘制Allan标准差对数曲线如图1所示。

如图1所示，在平均时间较小的部分，MEMS陀螺误差主要包含量化噪声；在平均时间稍大的区域则主要是角速度随机游走；而在几十到几百秒量级的平均时间范围内零偏不稳定性是主要的误差项。误差项分析结果与陀螺仪常见噪声类型吻合。Allan方差能够有效地辨识出各类噪声对MEMS陀螺性能影响的比重，为后续陀螺随机漂移模型预测提供依据。

2 灰色RBF神经网络

2.1 灰色累加生成

灰色模型中的GM(1，1)主要用于时间序列预测。不同于传统方法，灰色建模不依靠数学方法分析未知系统的特性，而是采用累加生成操作(AGO)方法逼近系统[11-13]。原始不规则序列经过累加生成后，序列规律性增强且系统随机性降低。灰色AGO过程如下：

1)设定一个原始数据序列

X0={x0(1),x0(2),x0(3)，…，x0(n-1),x0(n)}。

(3)

式中x0(i)(i=1,2,3，…，n)表示第i个数据点。

2)把原始序列各数据点依次累加的过程称为累加生成过程(AGO)，由累加生成过程所得的数列称为累加生成数列。令

X1={x1(1),x1(2),x1(3)，…，x1(n-1),x1(n)}。

(4)

3)对累加生成的序列X1可重构X0， 令

x0(k)=x1(k)-x1(k-1),k=2,3,4,…,n。

(5)

式中x0(1)=x1(1)， 此运算过程称为灰色累减生成(I-AGO)。

2.2 RBF神经网络

RBF神经网络是一种由输入层、隐层、输出层3部分所构成的前馈式神经网络[14]，具有最优逼近和全局优化的特点，在进行函数逼近时能有效克服局部最优问题，因此RBF神经网络广泛应用于非线性时间序列建模中。其中：输入层由原始信号组成；第二层隐层变换由非线性函数组成，相对于中心点径向对称；第三层的网络输出是隐层的线性函数加权求和所得(如图2)。

θ0表示RBF神经网络输出偏置，隐层中选取Gaussian函数作为RBF函数

(6)

式中：wi为第i个隐层节点的输出；ci为第i个高斯基函数的中心；βi为第i个隐层节点扩展常数，其决定了基函数围绕中心点的敏感域；‖.‖为欧几里得范数，表示x和ci之间的距离。RBF神经网络输出可由简单线性组合表示为

(7)

式中θi表示隐层到输出层的连接权值。

2.3 MEMS陀螺随机误差的灰色RBF建模

MEMS陀螺随机误差建模的准确度受随机性影响，随机性越大导致建模精度越低。灰色理论中的AGO对随机误差信号进行预处理后的数据符合一定指数变化规律；利用RBF神经网络对处理后的数据进行建模预测并对建模结果和已知数据进行分析，通过调整网络结构提高MEMS陀螺随机误差补偿精度。

灰色RBF神经网络即将灰色理论应用于神经网络，将二者优缺点结合起来，组成高精度预测模型。如图3所示，本文通过在RBF神经网络前端增加灰色累加处理、后端加入灰色累减过程进行灰色还原的嵌入型融合方式实现MEMS陀螺随机漂移模型的建立。

本文采用陀螺实测数据进行RBF神经网络在线训练，以陀螺仪时间序列数据w(n)作为输入。RBF输入层以陀螺前4个数据w(i-1)、w(i-2)、w(i-3)、w(i-4)(i=1,2,3,…，n)作为网络训练样本，以陀螺后一个数据w(i)为RBF输出层。训练过程可利用MATLAB神经网络工具箱RBF神经网络函数设定一定精度进行在线训练。

3 实验与结果分析

为验证本文所提灰色RBF神经网络建模方法的优势，对实验室现有的MTI-100型MEMS陀螺仪随机漂移进行实测，器件指标如表2所示。

表2 MTI-100型MEMS陀螺仪指标

3.1 逐项随机误差的Allan方差比对分析

由于MEMS陀螺随机误差中的高频部分主要对应白噪声，因此低频部分对应随机漂移。首先采用小波阈值去噪方法对陀螺输出信号的高频部分进行分离，然后采用灰色RBF网络对此三轴陀螺的漂移数据进行学习，分别比较它们在一定训练周期所能达到的误差精度。为验证论文所提方法的可靠性，截取10组数据，分别对MEMS陀螺原始信号、小波变换分离白噪声后的漂移信号和灰色RBF神经网络建模补偿后的信号进行Allan方差分析比较，得到如图4至图6所示的MEMS陀螺仪量化噪声、角度随机游走和零偏不稳定性的对比曲线。

通过对图4至图6的对比分析可看出，经过小波阈值去噪和灰色RBF神经网络预测建模补偿后的三轴MEMS陀螺仪输出都在一定程度上降低了量化噪声、角度随机游走和零偏不稳定性在其输出中的比重，而经过灰色RBF神经网络预测建模补偿后结果更为突出，各种随机误差均保持在0附近。将多组测试结果分别取平均后得到如表3所示的MEMS陀螺仪Allan方差分析结果。

表3 MEMS陀螺Allan方差分析

如表3所示，小波阈值去噪后的量化噪声、角度随机游走和零偏不稳定性相对MEMS陀螺仪原始信息均有较大幅度提高，经过灰色RBF补偿后的误差参数呈现2个数量级的提升。

3.2 灰色RBF建模补偿结果及分析

完成MEMS随机误差中所包含的量化噪声、角度随机游走和零偏不稳定性的Allan方差比对，可看出灰色RBF神经网络预测模型具有明显的单项误差补偿效果。为进一步验证论文所提方法对于提高MEMS陀螺输出精度的可行性，将灰色RBF神经网络预测模型对小波阈值分离后的随机漂移数据进行建模并补偿，得到MEMS陀螺原始信息与灰色RBF神经网络预测模型补偿后的对比曲线、补偿后残差分别如图7和图8所示。

如图7和图8所示，经过灰色RBF神经网络预测模型估计的陀螺输出角速率与陀螺仪原始输出具有较高的重合度，经比较后的漂移误差残差值限制在±0.002 (°)/s之间，显著地提高了MEMS陀螺输出信息的信噪比，验证了论文所提方案的有效性。

4 结束语

本文针对传统的多项式法对MEMS陀螺随机误差建模存在的难题，提出一种灰色RBF神经网络预测建模方法。基于MEMS陀螺输出信号Allan方差分析结果，采用灰色理论对白噪声分离后陀螺漂移误差进行灰化处理，结合RBF神经网络对灰化后陀螺漂移数据建模并补偿，得到高精度MEMS陀螺仪随机误差补偿模型。实验结果表明，提出的灰色RBF神经网络模型能够有效地预测出MEMS陀螺仪量化噪声、角度随机游走和零偏不稳定性的变化趋势，经过补偿后得到的陀螺漂移误差残差小于±0.002(°)/s，该结果验证了论文所提的灰色RBF模型具有较高的准确性。

[1] 宋吉磊，吴训忠，郭玲.微机电系统陀螺仪随机误差建模与滤波研究[J].导航与航天运载技术，2012，32(4)：35-38.

[2] 孙伟，丁伟，李瑞豹.基于小波降噪的MEMS惯导系统粗对准方法研究[J].传感技术学报，2015，28(6)：814-819.

[3] 宋丽君，秦永元，杨鹏翔.小波阈值去噪法在MEMS陀螺仪信号降噪中的应用[J].测试技术学报，2009，23(1)：33-36.

[4] 于旭东，魏学通，李莹，等.RBF神经网络在单轴旋转惯导系统轴向陀螺漂移辨识中的应用[J].国防科技大学学报，2012，34(3)：48-52.

[5] KARIM S, AMIN S K. On-line multivariable identification by adaptive RBF neural networks based on UKF learning algorithm[C]//The Chinese Control and Decision Conference (CCDC) .Proceedings of 2008 Chinese Control and Decision Conference.Yantai：CCDC，2008: 4754-4759.

[6] BARALD A P, BLOND A G, SATALINO A, et al. RBF two-stage learning networks exploiting supervised data in the selection of hidden unit parameters: an application to SAR data classification[C]//Institute of Electrical and Electronics Engineers(IEEE).Proceedings of IEEE 2000 International Geoscience and Remote Sensing Symposium.Hawaii: Institute of Electrical and Electronics Engineers, Inc., 2000: 672-674.

[7] 沈军，缪玲娟，吴军伟，等.基于RBF神经网络的光纤陀螺启动补偿及应用[J].红外与激光工程，2013，42(1)：119-124.

[8] 郝万亮，孙付平.基于Allan方差的陀螺随机误差分析[J].测绘与空间地理信息，2014，34(3)：23-25.

[9] 高宗余，方建军，于丽杰.MEMS传感器随机误差Allan方差分析[J].仪器仪表学报，2011，32(12)：2863-2868.

[10]赵思浩，陆明泉，冯振明.MEMS惯性器件误差系数的Allan方差分析方法[J].中国科学：物理学 力学 天文学，2010，40(5)：672-675.

[11]樊春玲，张静，金志华，等.一种新型的灰色RBF神经网络建模方法及其应用[J].系统工程与电子技术，2005，27(2)：316-319.

[12]DEJAMKHOOY A，DASTFAN A，AHMADYFARD A.Modeling and forecasting non-stationary voltage fluctuation based on grey system theory[J].IEEE Transactions on Power Delivery，2015，32(3)：1-1.

[13]于旭东，魏学通，李莹，等.RBF神经网络在单轴旋转惯导系统轴向陀螺漂移辨识中的应用[J].国防科技大学学报，2012，34(3)：48-52.

[14]李士心，王晓亮，翁海娜，等.基于灰色模型和RBF神经网络的MEMS陀螺温度补偿[J].中国惯性技术学报，2010，18(6)：742-746.

Modeling of MEMS gyroscope random errors based on grey model and RBF neural network

SUNWei，LIUDepeng，WENJian，WUZenglin

(School of Geomatics，Liaoning Technical University，Fuxin，Liaoning 123000，China)

In order to improve the accuracy of MEMS gyroscope，considering the characteristics that the grey cumulative and regressive operation could reduce the randomness of MEMS gyroscope，the paper proposed a MEMS random modeling method which combines the grey theory and radial basis function(RBF)：firstly，the random errors of the sample space composed of the gyro output data were analyzed with Allan variance；secondly，the random prediction model of MEMS gyroscope was built through the embeded coupling of grey cumulative and regressive process and RBF neural networks.Experimental result showed that the proposed method could effectively predict the random errors and improve the predicted output accuracy of MEMS gyroscope by comparing with measured data.

MEMS gyroscope；grey model；radial basis function neural networks；random error

2016-10-14

辽宁省高等学校杰出青年学者成长计划(LJQ2015044)；辽宁省自然科学基金(2015020078)；辽宁省“百千万人才工程”培养经费资助(辽百千万立项【2015】76号)。

孙伟(1984—)，男，黑龙江萝北人，教授，研究方向为惯性导航与组合导航技术。

孙伟，刘得朋，文剑，等.一种MEMS陀螺随机误差的灰色RBF神经网络建模方法[J].导航定位学报，2017，5(3)：9-13.(SUN Wei，LIU Depeng，WEN Jian，et al.Modeling of MEMS gyroscope random errors based on grey model and RBF neural network[J].Journal of Navigation and Positioning，2017，5(3)：9-13.)

10.16547/j.cnki.10-1096.20170303.

V249.322

A

2095-4999(2017)03-0009-05