多新息抗差—自适应卡尔曼滤波定位算法研究*

李雅梅， 康璐璐

(辽宁工程技术大学 电气与控制学院,辽宁 葫芦岛 125000)

多新息抗差—自适应卡尔曼滤波定位算法研究*

李雅梅， 康璐璐

(辽宁工程技术大学 电气与控制学院,辽宁 葫芦岛 125000)

针对移动机器人在定位过程中，由传感器测量误差和机器人模型引起的位姿误差导致系统定位精度急剧下降的问题，提出了一种多新息卡尔曼滤波算法。在标准卡尔曼滤波的基础上，当传感器测量值存在误差时，引入抗差权因子，通过改变误差测量值的权值提高滤波器的估计精度；当机器人位姿存在误差时，引入自适应因子，通过调整状态协方差矩阵的大小抵制位姿误差引起的滤波发散。同时，引入了多新息，即多个时刻的新息向量，进一步提高此非线性系统的精度。实验表明：当存在测量误差和位姿误差时，该滤波算法能有效提高定位精度。

抗差滤波; 自适应卡尔曼滤波; 权因子; 自适应因子; 多新息

0 引 言

移动机器人的定位指机器人在运动过程中根据所处环境的特征(路标)确定所处的位置[1]。解决定位误差问题最早最常用的方法就是扩展卡尔曼滤波(extended Kalman filtering,EKF)算法。针对传统EKF算法的多种缺陷，近年来,提出了很多改进算法。比如精密单点定位的抗差卡尔曼滤波根据精密单点定位的内部可靠性和观测值的随机性来改进定位精度[2]；无迹粒子滤波能较好地利用观测值提供的信息[3]。

根据定位过程中产生异常值的2个方面：机器人位置误差和姿势误差，提出了多新息抗差—自适应卡尔曼滤波。由于机器人的运动和传感器测量的过程中均存在不可避免的噪声，其中两个重要的噪声就是测量粗差和位姿误差[4]。为减小误差的影响，在标准卡尔曼滤波的基础上，引入了基于最小二乘权因子抗差估计和基于假设检验的自适应因子，构造抗差—自适应卡尔曼滤波，对系统进行了更精确估计。机器人自主定位系统很明显是一个非线性系统，因此，本文在以前单新息理论的基础上引入多新息理论，实现在强非线性系统中的精确定位[5]。

1 滤波算法

1.1 卡尔曼滤波

标准卡尔曼滤波的公式如下

Xk,k-1=φk,k-1Xk-1

(1)

(2)

(3)

Pk=(I-kkHk)Pk,k-1

(4)

Xk=Xk,k-1+kk(Zk-HkXk,k-1)

(5)

式中Xk-1为k-1时刻的状态估计;Xk,k-1为k-1时刻的状态预报值;Pk-1为k-1时刻的状态协方差矩阵;Pk,k-1为Xk,k-1的状态协方差矩阵;Kk为k时刻的卡尔曼滤波增益矩阵;Pk为k时刻测量更新的状态协方差矩阵;Xk为k时刻测量更新的状态估值。

1.2 结合抗差与自适应卡尔曼滤波

1.2.1 抗差估计

当观测值存在粗差时，抗差估计将粗差归入随机模型，通过调节随机模型中观测值方差的大小来调整粗差影响[6]。设方差膨胀公式为

(6)

式中H0为观测值中无误差；H1为含有粗差。含有粗差的观测值的方差扩大k倍，其相应观测值的权值也缩小k2倍,则抗差估计通过减小粗差观测值的权重减小误差。

在卡尔曼滤波中，测量新息定义为状态预估值和当前观测值的函数，可表示为

ek=Zk-HkXk,k-1

(7)

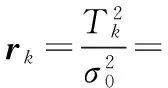
(8)

令

TD=χ2(nk)

(9)

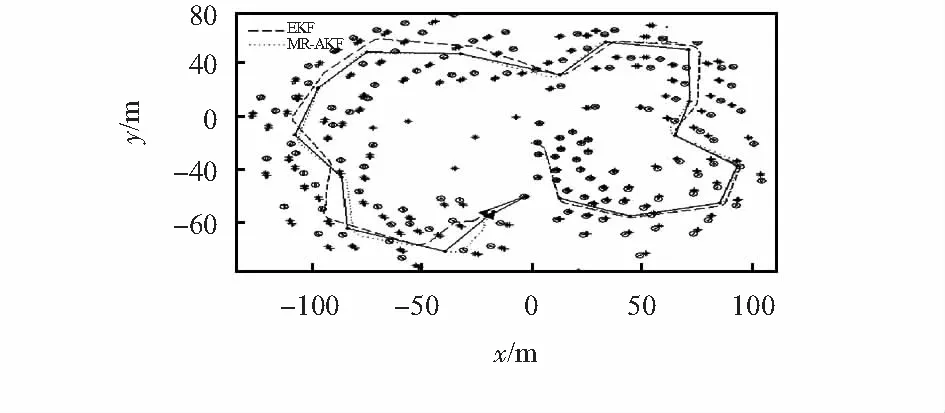
若rk

(10)

令

β=diag[β1β2…βn],

0<βi≤1,i=1,2,…,n

(11)

于是，相应的等价抗差协方差矩阵为

(12)

则式(3)可改为

(13)

当系统存在粗差时，抗差卡尔曼滤波通过增大相应观测噪声方差，减小观测值增益，提高了系统的估计精度。

1.2.2 自适应因子

为了抵制动力学模型异常产生的误差，在标准卡尔曼滤波的基础上引入自适应因子α，并将α作用于k时刻测量更新的状态协方差矩阵。式(2)可更新为

(14)

为了得到自适应因子α的值，作如下计算：

利用式(7)可得

(15)

由式(8)、式(9)可知,若rk

(16)

将式(15)代入式(16)有

(17)

为了解上式构造函数

(18)

上式在[1,+∞)为一个凸函数，因此，采用最陡下降法求解αk。

迭代初始选αk=1，当αk代入式(18)满足条件或者达到迭代次数，则停止迭代。最后将求得的αk代入式(14)。αk求解方法参照文献[7]。

2 多新息理论

本文要应用多新息理论，要将新息ek扩展为新息矩阵E(n,k)。为了适应兼容性，同理系统测量值Zk扩展为Z(n,k)，测量噪声rk扩展为r(n,k)，滤波增益矩阵kk扩展为k(n,k),代入式(5)有

Xk=Xk,k-1+k(n,k)E(n,k)

(19)

多新息卡尔曼滤波引入之前多个时刻的新息量，大大加强了数据的利用，实验表明,强非线性系统中，多新息卡尔曼滤波较单新息卡尔曼滤波有更好的鲁棒性和稳定性。虽然多新息卡尔曼滤波会比单新息卡尔曼滤波计算量加大，但相对于精度的提高，增加的计算量是可以接受的[8]。

3 仿真验证

3.1 系统建模

实验平台为Windows7操作系统，CPU为Intel i5—4170，主频为3.7 GHz。

实验所模拟的环境区域大小为200 m×200 m。有17个导航点、135个路标；机器人配有里程计、前轮转角传感器、激光测距仪、光电编码器获得机器人及环境信息；机器人速度为v=3 m/s，最大舵角为20°。

首先,利用一个非线性函数f(x)对状态转移进行建模，同时，状态的测量值由一个非线性函数h(x)建模

Xk+1=f(xk,uk)+qk

(20)

Zk+1=h(xk,uk)+rk+1

(21)

为了与多新息一致，将式(21)改为

(22)

状态矢量X由小车状态Xv和路标(特征)状态Xm组成。因此

X=[Xv,Xm]

(23)

(24)

系统使用激光传感器作为测速设备，使用光电编码器作为系统的速度计算，重力传感器用来确定系统的姿态。根据以上静态特征的位置估计定义地图。假设系统初始时没有观测特征，直角坐标系与小车的起始位姿一致，且小车的起始位姿确定。即，X=Xv=0和P=Pv=0。随后小车开始运动，Xv和Pv变为非零值。随着小车运动，进行第一次观测，则会产生新的特征，并开始出现Xm和Pm。相应的X和P也会随之增加[7]。随着小车运动，不断进行以上操作，进行定位。具体流程如图1。

图1 系统建模流程

3.2 仿真结果

机器人在由包含17个导航点、135个路标点确定的路径上运动。仿真结果如图2。实线为小车路径，虚线为小车在EKF下的真实路径；点线为小车在本文应用的滤波(MR-AKF)下的真实路径。星形线(*)为路标的实际位置；圆圈(o)为EKF仿真的路标的估计位置；十字线(+)为MR-AKF仿真的路标的估计位置。路标的估计位置和路线越接近实际位置说明系统的性能越好。

图2 仿真路线

图2给出了EKF和本文滤波(MR-AKF)的实际运动轨迹；图3给出了2种滤波算法与实际轨迹的整体误差；图4给出了2种滤波算法的运动模型定位误差；图5给出了两种滤波算法的测量误差。机器人在由包含15个导航点、135个路标的路径上运动。从图2～图4可以看出,机器人在转向角小于120°时，仿真路径和真实路径会有明显差异,这是由于转向角较小时，系统动力学模型的运行速度和朝向角度会很难估计[9]，容易引起误差,可以看出本文的算法较EKF有显著改善；从图2、图3、图5可以看出,系统刚开始运行，2种滤波算法均较精确，随着系统的运行误差也会越来越大，这是由于测量误差的累积，导致系统稳定性下降[10]；本文采用的算法也较EKF有明显改善；在系统运行到后半段时2种滤波算法均有所下降，一个很重要的因素是系统非线性的增加，本文采用的多新息抗差—自适应卡尔曼滤波较EKF效果好很多。从图2可以看出本文的滤波算法基本可以实现对系统的精确定位。

图3 EKF和MR-AKF整体误差对比

图4 EKF和MR-AKF运动模型误差对比

图5 EKF和MR-AKF测量误差对比

4 结束语

研究了在系统存在测量误差和动力模型误差时，应用多新息抗差—自适应卡尔曼滤波对测量误差和动力学模型误差进行更正，引入的多新息概念使系统即使处于强非线性状态也能很精确的实现定位，定位过程中均有较强的鲁棒性，基本达到精确定位的目的。

[1] 高云峰，周 伦，吕明睿,等.自主移动机器人室内定位方法研究综述[J].传感器与微系统，2013,32(12)：1-5.

[2] 许长辉，高井祥，胡 洪,等. 精密单点定位的抗差卡尔曼滤波研究[J].中国矿业大学学报，2014,33(12)：38-41.

[3] 毛 铃，李振波，张大伟,等.基于红外传感器的移动机器人定位研究[J].传感器与微系统，2009,26(2)：159-162.

[4] 季秀才,郑志强，张 辉.SLAM问题中机器人定位误差分析与控制[J].自动化学报，2008,34(3)：323-330.

[5] 吕国宏，秦品乐，苗启广,等.基于多新息理论的EKF算法研究研究 [J].小型微型计算机系统，2016,3(3)：576-58.

[6] 苗岳旺.SINS/GPS组合导航数据处理方法研究[D].郑州:信息工程大学,2013.

[7] 李 刚，蔡成林，李思敏,等.抗差与自适应组合的卡尔曼滤波算法在动态导航中的研究 [J].重庆邮电大学学报,2015,27(1)：37-43.

[8] Amitava Chatterjee.Vision-based autonomous robot naviga-tion[M].连晓锋,译.北京:机械工业出版社,2014.

[9] 雷 创.基于自适应EKF的相对导航算法研究[J].现代导航，2014,4(2):113-116.

[10] 陈航科，张东升，盛晓超,等.基于Kalman滤波算法的姿态传感器信号融合技术研究[J].传感器与微系统，2013,32(12):82-85.

李雅梅(1966-),硕士,副教授,主要从事计算机控制与应用、智能检测、数字信号处理等领域研究工作。

康璐璐(1991-),通讯作者，硕士研究生,主要研究方向为检测技术与自动化装置研究，E—mail:1980265487@qq.com。

Research on multi-innovation robust adaptive Kalman filtering positioning algorithm*

LI Ya-mei, KANG Lu-lu

(College of Electrical and Control，Liaoning Technical University，Huludao 125000,China)

In the positioning process, the positioning accuracy of mobile robot drops sharply because of the sensor measurement error and the pose error caused by the robot model.In view of this phenomenon,a new algorithm based on multi-innovation Kalman filtering(MR-AKF)is proposed.Based on the standard Kalman filter,when the measured value of the sensor is error,the robust weighting factor is introduced,and the estimation accuracy of the filter is improved by changing the weight of the error measurement value;when the robot pose is error,an adaptive factor is introduced to resist the filtering divergence caused by the pose error by adjusting the size of the state covariance matrix.At the same time,introduce multi-innovation which is the innovation vector of multiple moments to further improve the accuracy of the nonlinear system.The experimental results show that the filtering algorithm can effectively improve the positioning accuracy in the presence of measurement errors and pose errors.

robust filtering; adaptive Kalman filtering; weight factor; adaptive factor; multi-innovation

10.13873/J.1000—9787(2017)09—0038—03

2016—10—17

国家自然科学基金资助项目(51274118)

TP 31

A

1000—9787(2017)09—0038—03