基于扩展有限元的应力强度因子的位移外推法1)

周 博 薛世峰

(中国石油大学储运与建筑工程学院，山东青岛266580)

基于扩展有限元的应力强度因子的位移外推法1)

周 博2)薛世峰

(中国石油大学储运与建筑工程学院，山东青岛266580)

针对平面裂纹问题，阐述了扩展有限元法的单元位移模式、推导了扩展有限元法的控制方程、介绍了特殊单元的数值积分技术.基于最小二乘法，建立了应力强度因子位移外推法的计算公式.利用MATLAB编写计算程序，对平面裂纹问题用扩展有限元法进行了计算.基于扩展有限元法的计算结果，分别利用位移外推法和相互作用积分法，对平面裂纹的应力强度因子进行了计算.计算结果表明,位移外推法比相互作用积分法能更方便和准确地计算平面裂纹的应力强度因子.

扩展有限元法，应力强度因子，位移外推法，相互作用积分法

在工程实际中经常发生断裂引起的破坏事故，如地震所致地质构造和工程结构的开裂、压力管道的裂纹失稳扩展、机械构件的疲劳断裂等，这些事故均可以对人民生命和财产造成重大损失.裂纹的萌生是不可避免和难以量化研究的，确定裂纹产生后是否继续扩展或发生止裂的断裂力学具有理论和实际意义[1].有限元法理论基础成熟且通用性强，是处理断裂力学问题的常用数值方法.在应用有限元法处理裂纹时，需要将裂纹设置为单元的边，将裂纹尖端设置为单元的节点.为提高计算精度在裂纹尖端处还需使用奇异单元和进行网格加密，在模拟裂纹扩展时还需要重新划分网格.因此有限元法处理断裂力学问题的过程，相对繁琐和困难，遇到复杂问题时就可能无能为力.

1999–2002年，Belytschko等[24]，在传统有限元法的框架内建立了扩展有限元法，很好地解决了由于材料或几何等因素引起的不连续问题，特别适合于处理断裂力学问题，近年来正不断得到成功应用.2005年，余天堂[5]详细介绍了扩展有限元法求解裂纹体问题的基本过程，利用相互作用积分法计算了I型裂纹的应力强度因子，取得了良好的计算结果.2007年，方修君等[67]基于扩展有限元法基本原理，开发了ABAQUS调用的黏聚裂纹模型，对三点弯曲梁的裂纹扩展过程进行了模拟，结果表明扩展有限元法对非连续位移场的求解不依赖于单元边界，是模拟裂纹扩展的有效方法.2008年，懂玉文等[8]提出了通过求解扩展有限元法总体刚度方程中的附加自由度，直接计算应力强度因子的计算方法，取得了良好数值计算结果.2009年，宋娜等[9]研究了单元类型、网格密度、J积分区域半径等因素对扩展有限元法计算应力强度因子的精度的影响，结果表明利用扩展有限元法计算应力强度因子时，上述因素对计算结果精度的影响不显著.2010年，余天堂[10]建立了闭合型摩擦裂纹问题的扩展有限元法线性互补模型，将裂纹面非线性摩擦接触转化为一个无需迭代求解的线性互补问题，取得了良好的计算效果.

2011年，茹忠亮等[11]分析了应力强度因子J积分方法中积分区域、网格密度等因素对扩展有限元法计算精度的影响，给出了计算应力强度因子的合适参数，有效提高了应力强度因子的计算精度. 2012年，杜修力等[12]利用扩展有限元法模拟了湿筛混凝土单轴拉伸作用下混凝土板的细观断裂破坏过程，分析了混凝土裂纹萌生、扩展的过程及破坏形态.2013年，茹忠亮等[13]建立了预置裂纹混凝土梁的三维扩展有限元模型，对钢筋混凝土梁的复合断裂过程进行了模拟分析，取得了良好的计算结果.2014年，傅玉珍等[14]利用扩展有限元法模拟了冲击载荷作用下混凝土巴西圆盘的裂纹扩展过程，分析了应力场分布规律和网格形态对计算精度的影响；师访等[15]基于扩展有限元法，研究了正交各向异性岩体的应力强度因子和裂纹扩展特性，模拟了四点弯曲正交各向异性岩体式样的裂纹扩展过程，详细分析了弹性模量比对裂纹扩展行为的影响；盛茂等[16]建立了水力压裂问题的扩展有限元法，将缝内水压转化为单元等效节点力，利用相互作用积分法计算缝尖的应力强度因子，采用最大能量释放率准则作为裂纹扩展判据，模拟了水力压裂裂纹扩展路径.2015年，江守燕等[17]基于扩展有限元法，建立了求解双材料界面裂纹应力强度因子的相互作用积分法，对双材料界面裂纹的应力强度因子进行了计算.

计算断裂参数是断裂力学的重要内容，应力强度因子、J积分、应变能释放率是断裂力学中三个最基本的断裂参数.应力强度因子反映了弹性裂纹尖端应力场的强弱，J积分描述了由于裂纹存在所吸收的能量，应变能释放率描述的是产生裂纹面所需要的能量.对于线弹性材料，这三个断裂参数可通过材料参数联系起来，且J积分和应变能释放率是等价的.本文针对弹性平面裂纹问题，阐述了扩展有限元法平面4节点等参单元的位移模式，推导了平面裂纹的扩展有限元法控制方程，介绍了特殊单元的数值积分方法.基于最小二乘法和扩展有限元法的计算结果，建立了应力强度因子位移外推法的计算公式.利用MATLAB编写相关计算程序，对平面裂纹问题用扩展有限元法进行了计算.基于扩展有限元法的计算结果，分别利用位移外推法和相互作用积分法，对平面裂纹的应力强度因子进行了计算.计算结果表明，本文建立的基于扩展有限元法的应力强度因子的位移外推法，能方便和准确地计算平面裂纹的应力强度因子.

1 扩展有限元法

1.1 位移模式

扩展有限元法的基本原理是基于单位分解思想，在传统有限元法的位移模式中加进一些加强函数以反映特殊单元位移场的不连续性.扩展有限元法在分析裂纹问题时，计算网格和裂纹是相互独立的，比传统有限元法处理裂纹问题方便很多.在扩展有限元法的具体计算过程中，通过水平集函数来识别和追踪裂纹及其扩展路径.

对于平面裂纹问题，扩展有限元法的建模包括两部分：一是不考虑裂纹的几何形状和位置，对计算区域进行网格划分；二是对和裂纹接触的单元采用特殊的位移模式，改进裂纹附近位移场的数值精度.

如图1所示含裂纹平面结构的计算网格，其中的单元类型有三类：(1)不接触裂纹的常规单元，节点无特殊标记；(2)裂纹贯穿单元，节点用方块标记；(3)包含裂纹尖端单元，节点用圆圈标记.对于不接触裂纹的常规单元，其位移模式的选择和有限元法位移模式的选择完全相同，即

其中,Ni为单元形函数，ui为节点位移分量.

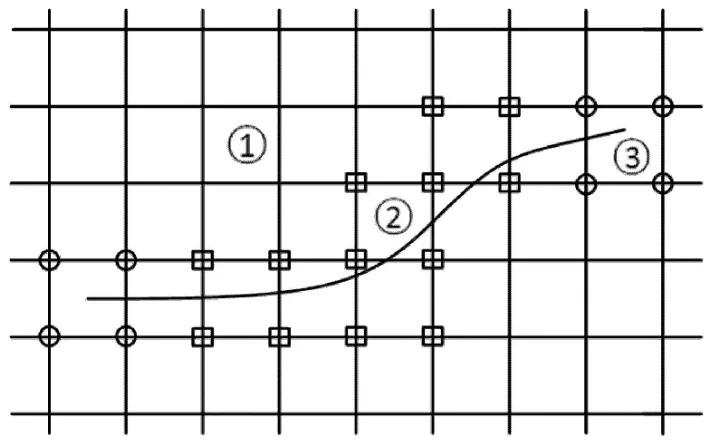
图1 含裂平面结构的计算网格

对于裂纹贯穿单元，单元位移模式[4]为

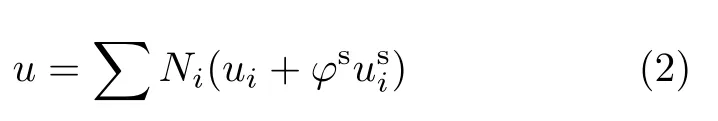
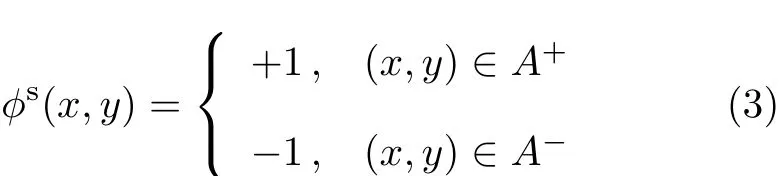
式中，A+和A-分别代表如图2所示的裂纹贯穿单元内位于裂纹两侧的区域.

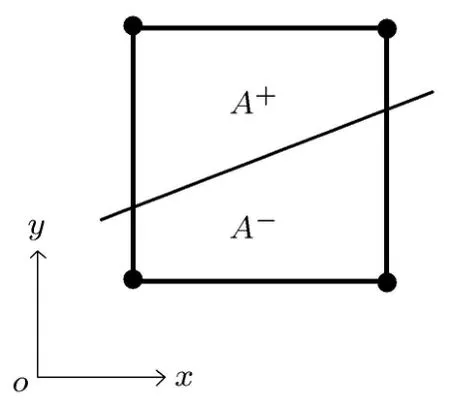
图2 裂纹贯穿单元的区域划分

对于包含裂纹尖端单元，单元位移模式[4]为

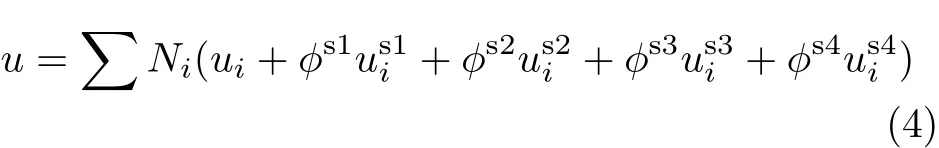
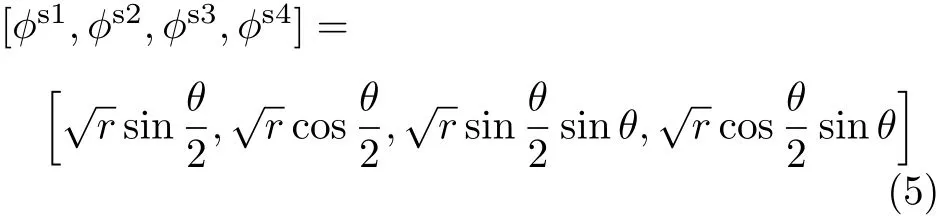
其中r和θ为如图3所示裂纹尖端局部极坐标系内的极坐标.

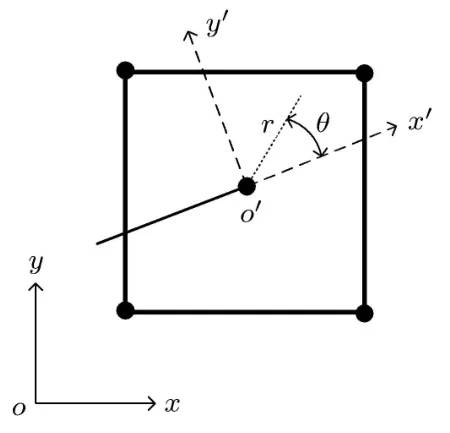
图3 包含裂纹尖端单元的裂纹尖端局部坐标系

1.2 控制方程

和传统有限元法控制方程的推导类似，扩展有限元法的控制方程也可以根据虚功原理得到.设含裂纹体结构的虚位移列阵为δu，由虚位移引起的虚应变列阵为δε，根据虚位移原理得到

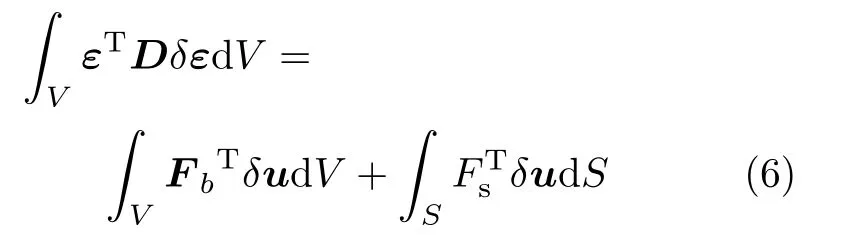
其中,ε为应变列阵，Fb为体力列阵，Fs为面力列阵，D为弹性矩阵.对于平面应力问题

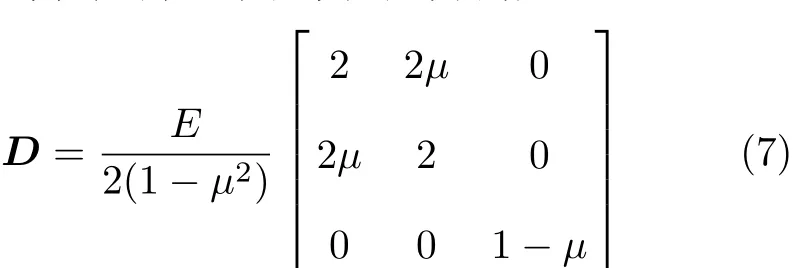
其中E和µ分别为弹性模量和泊松比.若将式(7)中的E和µ分别用和替换，即可得到平面应变问题的弹性矩阵.

将单元位移模式式(1)、式(2)、式(4)带入式(6)，得到含裂纹体结构的扩展有限元法的整体控制方程为其中,K为结构刚度矩阵，u′为节点未知量列阵，P为节点载荷列阵.和传统有限元法不同的是，节点未知量列阵u′中不仅包括节点位移分量ui，还包括式(2)和式(4)中节点增强变量.

和传统有限元法相似，扩展有限元法的结构刚度矩阵K，可其由单元刚度矩阵，按照对号入座的方法集合而成.不同的是在扩展有限元法中，不同种类单元的单元刚度矩阵的规模大小是不同的.以平面四节点等参元为例，在扩展有限元法中，所有单元刚度矩阵中的子矩阵可统一表示为

其中,non,cut和tip分别代表常规单元、裂纹贯穿单元和包含裂纹尖端单元，Bαi为几何子矩阵.

1.3 特殊单元积分

在利用式(9)计算单元刚度矩阵时，涉及到数值积分运算，对于平面四节点等参元，式(9)可以转化为

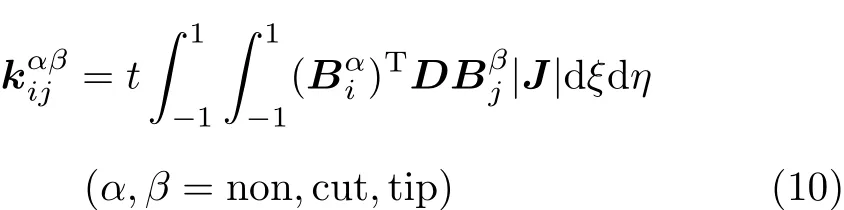
其中,J为描述单元整体坐标 (x,y)和局部坐标(ξ,η)间导数关系的雅可比矩阵的行列式.对于常规单元，积分式(10)计算和有限元法相同，采用高斯积分，取4个积分点就可以满足精度要求.

对于非常规单元，积分式(10)是不连续函数的积分，可以将含裂纹的单元沿着裂纹所在位置分割成若干个四边形子域，在每个子域进行4个积分点的高斯积分，再将各子域内的积分相加，得到整个单元的积分，具体分割方案如图4所示.

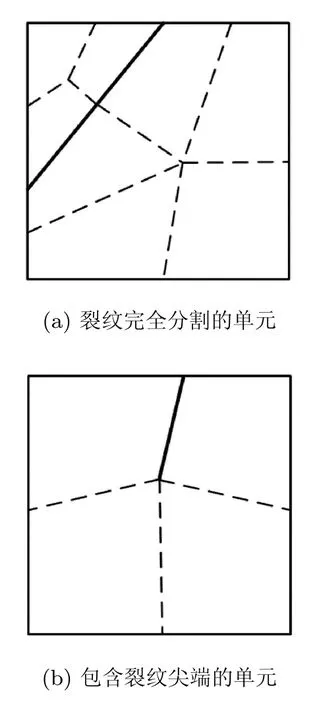
图4 非常规单元的分割方案

2 应力强度因子的位移外推法

2.1 应力强度因子

图5为含裂纹的无限大板及其坐标系.I型和II型裂纹应力强度因子[19]分别为

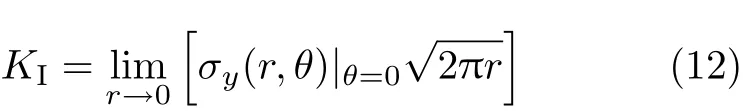
和

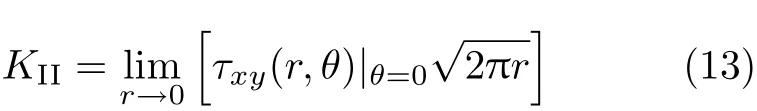
裂纹尖端附近的位移场[19]为

其中

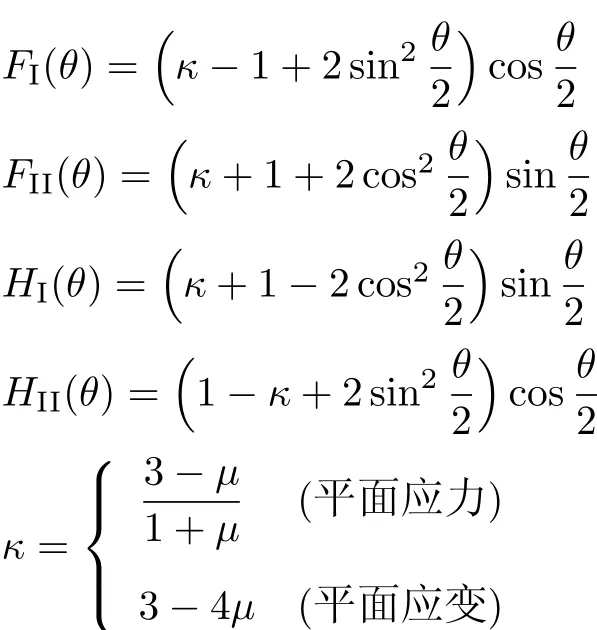
图5 无限大板内裂纹及坐标系

2.2 位移外推法

根据式(14b)，可知当θ=π且r→0时

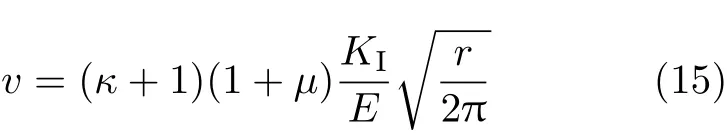
因此，I型裂纹的应力强度因子还可以定义为

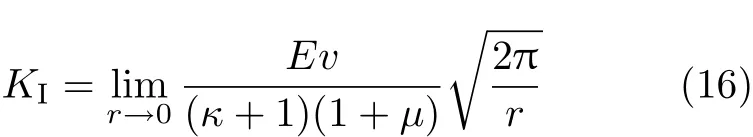
根据式(16)，利用

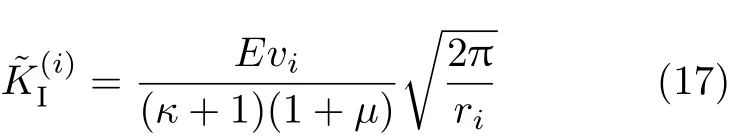
根据式(16)的定义，可知式(18)中等号右端的系数C2即I型裂纹的应力强度因子KI的近似值，因此可以将式(18)改写为

根据式(17)和式(19)，可得到所有数据点的偏差平方和为

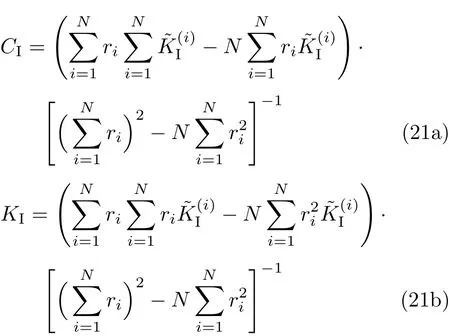
式(21b)即为I型裂纹应力强度因子位移外推法的计算公式.

根据式(14a)，可知当θ=π且r→0时，

因此，II型裂纹的应力强度因子可以定义为

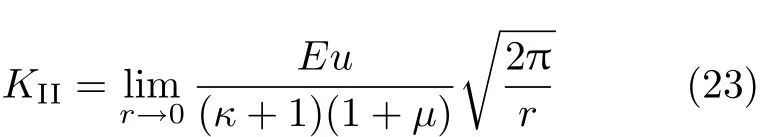
根据II型裂纹的应力强度因子的定义式(31)，利用

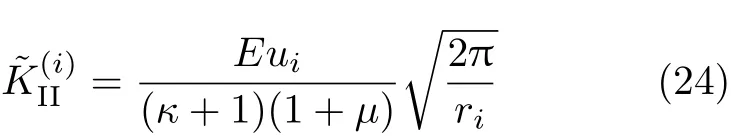
与式(19)分析过程相似，可以设

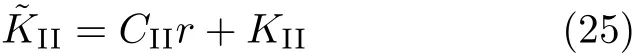
并利用最小二乘法可以得到

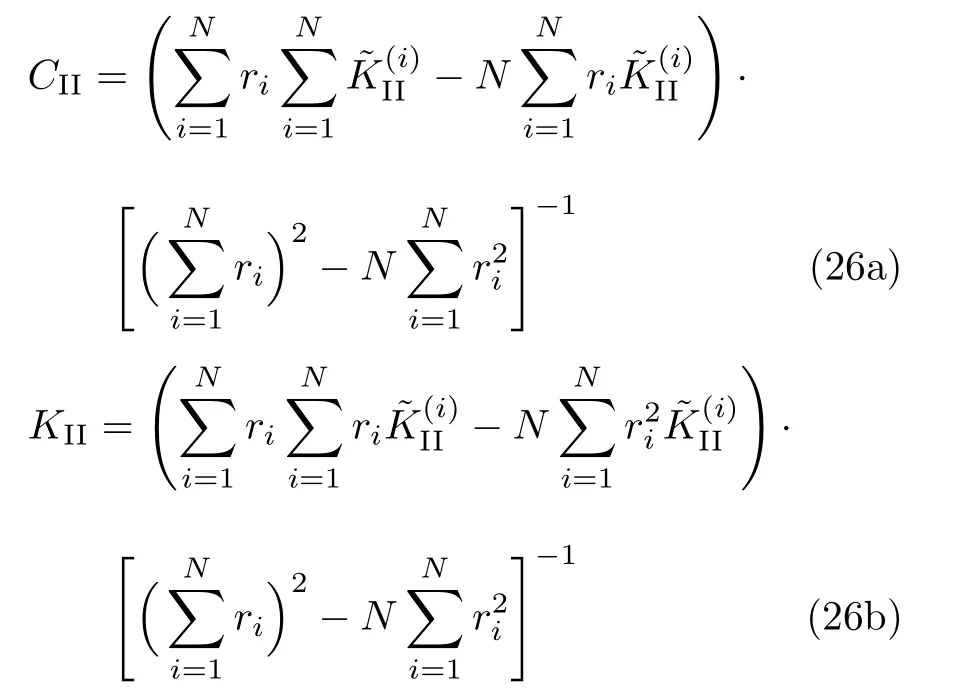
式(26b)即为II型裂纹的应力强度因子位移外推法的计算公式.

3 数值算例

利用MATLAB编写计算程序，对平面裂纹问题用扩展有限元法进行计算.基于扩展有限元法的计算结果，分别利用本文介绍位移外推法和文献[18]介绍的相互作用积分法，对平面裂纹的应力强度因子进行计算.图6为有中心裂纹的有限宽板，其宽和高分别为2w和2h，裂纹长度为2a，在上下两端承受均匀拉伸应力σ，根据对称性，在扩展有限元模拟时可取右半部为计算对象，计算中用到几何尺寸、材料参数和外载荷列于表1中，其中E和µ为弹性模量和泊松比.与有限元法相比较，用扩展有限元法计算裂纹问题的结果与网格的关系不大，不必在裂纹尖端处加密网格.为保证数值精度，在数据拟合时，极半径r的取值范围不能过大，通常取单元边长的5～15倍即可.

图6 有中心裂纹的有限宽板

表1 计算模型的几何尺寸、材料参数和外载荷

图7为扩展有限元法的计算模型，其中长度单位为m，中间的粗实线代表裂纹所在位置，水平方向和竖直方向的单元数量分别为50和101，单元类型为平面应力四节点等参元.边界条件为：x=0的左侧边的水平位移u=0；在裂纹下侧离裂纹垂直距离最短的、右侧4个节点的竖直位移v=0.外力边界条件为：在y=1和y=-1的上下两边，施加σ=10MPa拉伸静载荷.

图8为根据节点位移分量，绘制的扩展有限元法计算模型的变形图，为便于观察与分析计算模型的变形规律，图中的节点位移分量被放大了2000倍.不难发现计算模型的变形图所反映的变形规律，符合计算模型中的位移边界条件和外载荷条件，因此根据扩展有限元法计算出的节点位移符合实际情况.

图9为根据节点位移幅值，绘制的计算模型位移幅值云图，其中的位移幅值单位为m.可以看出计算模型的位移幅值，关于y=0描述的水平线具有对称性，这符合计算模型的位移边界条件和外力边界条件所决定的变形规律.

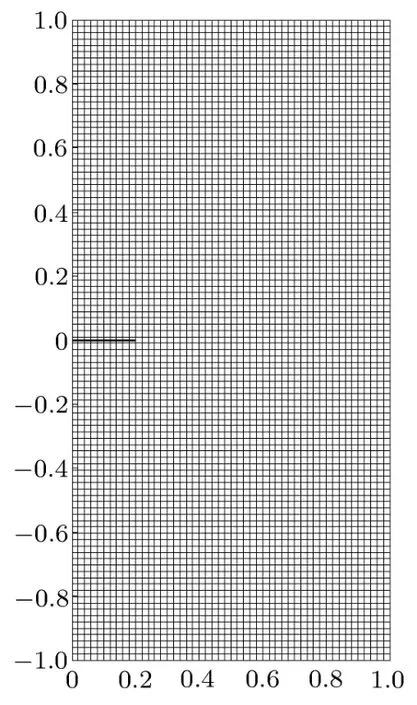
图7 扩展有限元法的计算模型

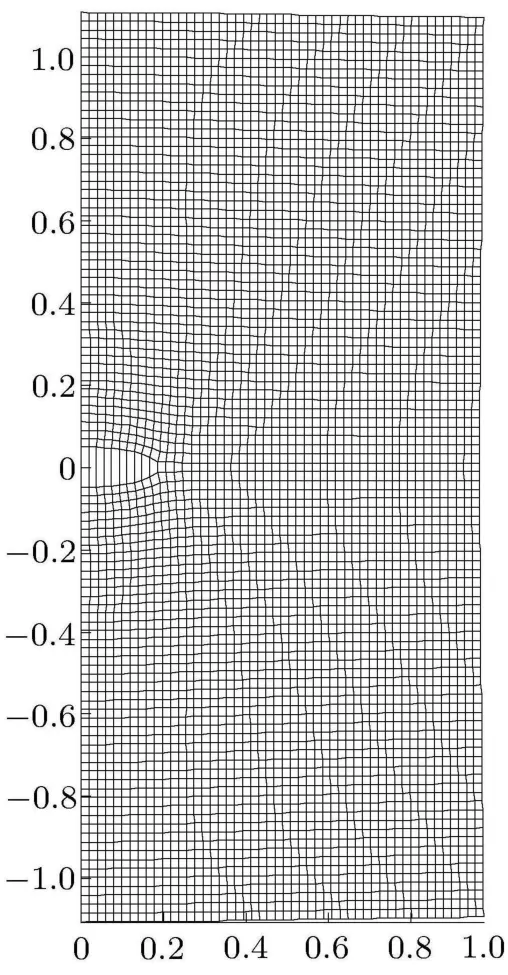
图8 计算模型的变形图

图10为根据节点竖向位移分量，绘制的计算模型竖向位移云图，其中竖向位移单位为m.可以看出计算模型的竖向位移，关于y=0描述的水平线具有反对称性，这符合计算模型的位移边界条件和外力边界条件所决定的变形规律.

图9 计算模型的位移幅值云图

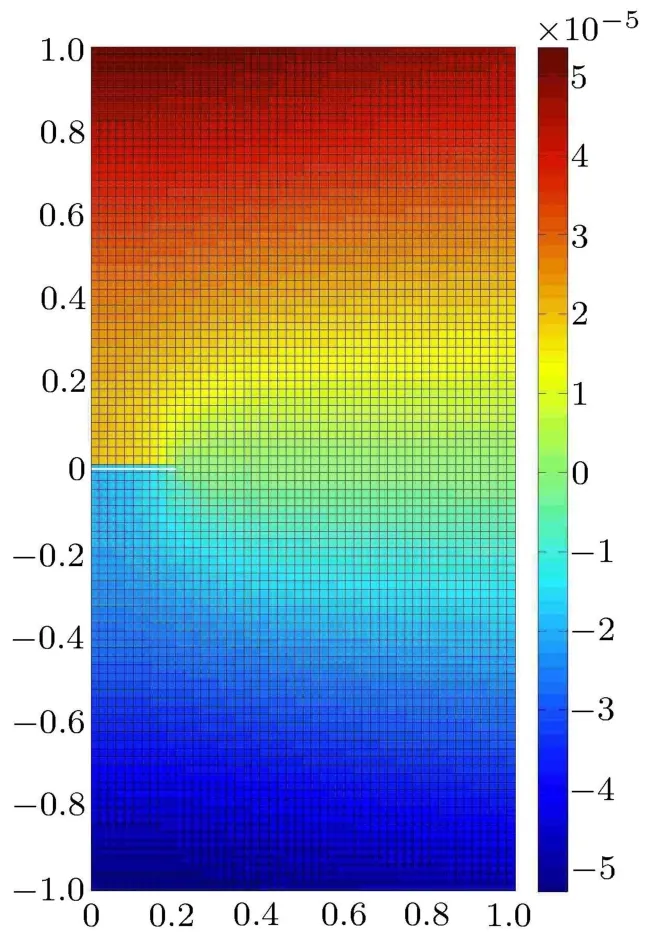
图10 计算模型的竖向位移云图

图 11为利用扩展有限元法计算出裂纹面附近节点竖向位移，通过MATLAB编写位移外推法计算程序，得到位移外推法数据拟合曲线，其中的星号标出的点为利用式(24)构造的数据点虚线为利用式(26)和式(29)拟合的曲线，曲线纵坐标截距即为利用式(29b)计算出的I型裂纹的应力强度因子，具体结果列于表2中.

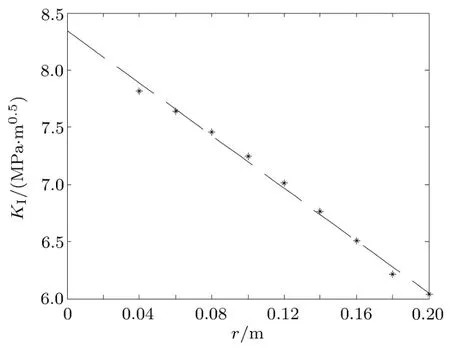
图11 位移外推法的拟合曲线

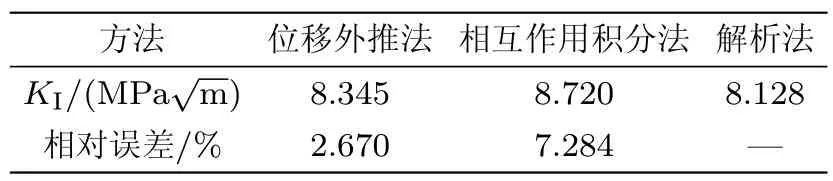
表2 不同方法的计算结果

结合前面扩展有限元法的结算结果，利用MATLAB编写相互作用积分法的计算程序，计算I型裂纹的应力强度因子，结果也列于表2中.为便于比较两种数值算法的精度，利用文献[19]中的解析公式

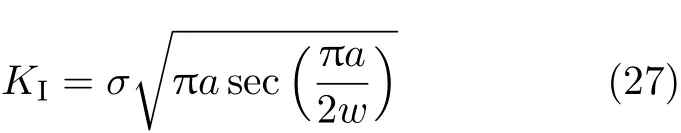
计算I型裂纹的应力强度因子，并计算两种数值方法与解析法的相对误差，结果均列于表2中.比较两种数值算法与解析法计算结果的相对误差，可以发现位移外推法的计算精度高于相互作用积分法的计算精度.而位移外推法的求解过程和程序设计，比相互作用积分法的求解过程和程序设计简单很多.因此本文建立的基于扩展有限元的位移外推法，能够更高效和准确地计算平面裂纹的应力强度因子.

4 结论

介绍了扩展有限元法基本原理，阐述了平面裂纹问题的四节点等参元单元的位移模式，推导了扩展有限元法的控制方程，介绍了特殊单元的数值积分方法.基于最小二乘法和扩展有限元法的计算结果，建立了应力强度因子位移外推法的计算公式.利用MATLAB编写了相关计算程序，对平面裂纹问题用扩展有限元法进行了计算.结合扩展有限元法的计算结果，分别利用位移外推法和相互作用积分法，对平面裂纹的应力强度因子进行了计算.数值计算与解析结果的对比表明,位移外推法比相互作用积分法能更方便和准确地计算平面裂纹的应力强度因子.

1范天佑.断裂理论基础.北京:科学出版社,2003:73-112

2 Belytschko T,Black T.Elastic crack growth in f i nite elements with minimal remeshing.International Journal for Numerical Method in Engineering,1999,45(5):601-620

3 Moes N,Dolbow J,Belytschko T.A f i nite element method for crack growth without without remeshing.International Journal for Numerical Method in Engineering,1999,46(1): 131-150

4 Mose N,Belytschko T.Extended f i nite element method for cohesive crack growth.Engineering Fracture Mechanics, 2002,69(7):813-833

5余天堂.含裂纹体的数值模拟.岩石力学与工程学报,2005,24: 4432-4439

6方修君,金峰,王进廷.基于扩展有限元法的粘聚裂纹模型.清华大学学报(自然科学版),2007,47(3):344-347

7方修君,金峰.基于ABAQUS平台的扩展有限元法.工程力学,2007,24(7):6-10

8懂玉文,余天堂,任青文.直接计算应力强度因子的扩展有限元法.计算力学学报,2008,25(1):72-77

9宋娜,周储伟.扩展有限元裂尖场精度研究.计算力学学报, 2009,26(4):544-547

10余天堂.摩擦接触裂纹问题的扩展有限元法.工程力学,2010, 27(4):84-89

11茹忠亮,朱传锐,张友良等.裂纹问题的扩展有限元法研究.岩土力学,2011,32(7):2171-2176

12杜修力,金浏,黄景琦.基于扩展有限元法的混凝土细观断裂破坏过程模拟.计算力学学报,2012,29(6):940-947

13茹忠亮，申葳，赵洪波.基于扩展有限元法的钢筋混凝土梁复合断裂过程模拟研究.工程力学，2013,30(5):215-220

14傅玉珍,张华,谈政.基于扩展有限元的巴西圆盘动态裂缝扩展分析.四川建筑科学研究,2014,40(2):47-54

15师访,高峰,杨玉贵.正交各向异性岩体裂纹扩展的扩展有限元法研究.岩土力学,2014,35(4):1203-1210

16盛茂，李根生.水力压裂过程的扩展有限元数值模拟方法.工程力学，2014,31(10):123-128

17江守燕，杜成斌，顾冲时等.求解双材料界面裂纹应力强度因子的扩展有限元法.工程力学，2015,32(3):22-27

18庄茁，柳占立，成斌斌等.扩展有限单元法.北京：清华大学出版社，2012

19薛世峰，侯密山.工程断裂力学.东营：中国石油大学出版社，2011

(责任编辑:刘希国)

DISPLACEMENT EXTRAPOLATION METHOD FOR STRESS INTENSITY FACTOR BASED ON EXTENDED FINITE ELEMENT METHOD1)

ZHOU Bo2)XUE Shifeng
(College of Pipeline and Civil Engineering,China University of Petroleum,Qingdao 266580,Shandong,China)

The element displacement modes of the extended f i nite element method for plane crack problems are discussed in this paper.The governing equations for the extended f i nite element method are derived based on the principle of virtual work.The numerical integration technique is adopted for special elements.The displacement extrapolation method is formulated to calculate the stress intensity factor based on the least square method.The numerical computation programs are developed by using the MATLAB,and the numerical calculations are carried out by the extended f i nite element method for the problem of plane crack.Based on the results of the extended f i nite element method,the stress intensity factors of plane crack are calculated by the displacement extrapolation method and the interaction integral method,respectively.Numerical results show that with the displacement extrapolation method,the stress intensity factors can be obtained more easily and precisely than the interaction integral method.

extended f i nite element method,stress intensity factor,displacement extrapolation method,interaction integral method

O346,TB115

：Adoi：10.6052/1000-0879-16-413

2016–12–20收到第1稿，2017–02–05收到修改稿.

1)国家自然科学基金(11472309)和中石油重大专项(2012-ZG-002)资助项目.

2)周博，教授.E-mail:zhoubo@upc.edu.cn

周博,薛世峰.基于扩展有限元的应力强度因子的位移外推法.力学与实践,2017,39(4):371-378

Zhou Bo,Xue Shifeng.Displacement extrapolation method for stress intensity factor based on extended f i nite element method.Mechanics in Engineering,2017,39(4):371-378