基于解耦滑模控制的桥式吊车系统的抗摆控制

于涛，杨昆，赵伟

（1.辽宁工业大学机械工程与自动化学院，辽宁锦州121001；2.北京印刷学院信息工程学院，北京102600）

基于解耦滑模控制的桥式吊车系统的抗摆控制

于涛1，杨昆1，赵伟2

（1.辽宁工业大学机械工程与自动化学院，辽宁锦州121001；2.北京印刷学院信息工程学院，北京102600）

针对欠驱动桥式吊车系统的抗摆控制问题，提出一种新型的解耦滑模控制算法。相比于传统解耦滑模控制算法，该控制算法采用可导的中间变量来定义系统的第二层滑动面，并利用等效控制关联增益法来调整解耦滑模控制器的切换增益；不但解决解耦滑模控制器等效控制的求取问题，而且能够有效降低解耦滑模控制器的抖振幅度。应用Lyapunov方法和Barbalat引理证明系统各层滑动面的渐近稳定性，并通过数值仿真实验验证所提出的控制算法的有效性。与已有控制算法的对比结果表明，该控制算法具有较好的控制性能和抖振抑制特性。

桥式吊车；欠驱动；抗摆控制；解耦滑模控制

0 引言

桥式吊车是工业领域中一种非常重要的起重运输机械，在码头、车间、仓库等工业场所应用广泛。桥式吊车在吊运过程中不可避免地会出现负载摆动现象，导致其产生的主要因素是台车的加减速和来自外界的干扰。负载摆动现象会给工业生产带来极大危害，如损坏货物、伤害人员等。同时由于这种摆动现象的存在，也会降低桥式吊车的吊运效率。基于桥式吊车系统这一特征，其抗摆控制问题受到了控制领域研究者的广泛关注。

目前，桥式吊车系统的抗摆控制方法主要有部分反馈线性化控制[1]、自适应PID控制[2]、无源性控制[3]、迭代学习控制[4]、信息融合控制[5]、轨迹跟踪控制[6]、智能控制[7-8]、滑模控制[9]等。桥式吊车是一种典型的欠驱动系统，文献[10]针对此类系统提出一种解耦滑模控制方法。但其控制器的等效控制含有中间变量的导数，而饱和函数型中间变量是不可导的，因此对于传统解耦滑模控制方法[10-12]而言，系统的等效控制不能求得。针对此问题，文献[10-12]将中间变量的导数项视为干扰项，但由于该导数项并不存在，导致切换增益的选取变得较为困难。一般而言，需要选取较大的切换增益，但同时也会加剧系统抖振。

针对传统解耦滑模控制方法存在的问题，本文提出了一种新型的解耦滑模控制方法，并基于该控制方法设计了桥式吊车系统的抗摆控制器。该控制器能够保证闭环系统的稳定性，并且可以减轻控制系统的抖振。仿真实验结果验证了该控制器的有效性。

1 桥式吊车系统的动力学模型

桥式吊车系统的结构如图1所示，负载通过长度为l的绳索悬挂在台车上，台车和负载在垂直平面（X-O-Y平面）内运动。设M和m分别为台车和负载的质量，u为作用在台车上的控制力，x为台车相对于原点O的水平位移，θ为绳索相对于垂直方向摆动的角度。

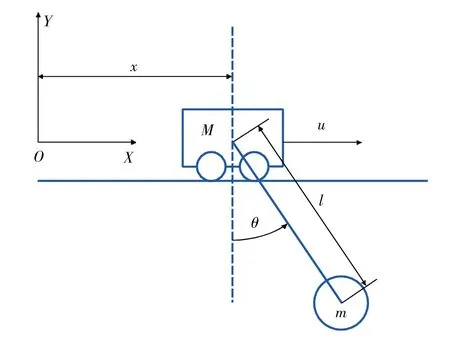
图1 桥式吊车系统的结构

忽略各种摩擦和绳索长度的变化，利用拉格朗日方程可得桥式吊车系统的动力学模型为

式中g为重力加速度。

由式（1）可见，桥式吊车系统是一个具有2个自由度和1个控制输入的欠驱动机械系统。

定义状态矢量X=[x，x˙，θ，θ˙]T，则系统动力学模型的状态空间形式为

式中xi（t）为系统的第i个状态变量，各非线性函数的表达式分别为

2 抗摆控制器设计

对于式（2）所示的桥式吊车系统，根据其状态构成将整个系统划分为如下2个二阶子系统：

对子系统A，定义第一层滑动面s1为

式中：xd——台车的目标位置；

c1——正常数。

对于桥式吊车系统的抗摆控制，负载的摆角和角速度的期望目标值均为零（即θd=θ˙d=0）。因此，设计子系统B的第一层滑动面s2为

式中c2为正常数。

为建立2个子系统滑动面s1和s2之间的联系，利用子系统B的滑动面s2来构造一个可导的中间变量：

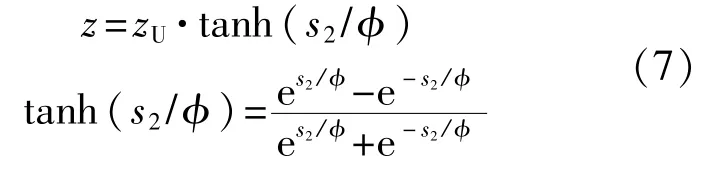
式中0〈zU〈1，φ为正常数。

将中间变量z嵌入子系统A的滑动面s1中，可得系统的第二层滑动面为

对式（7）求导，可以得到：

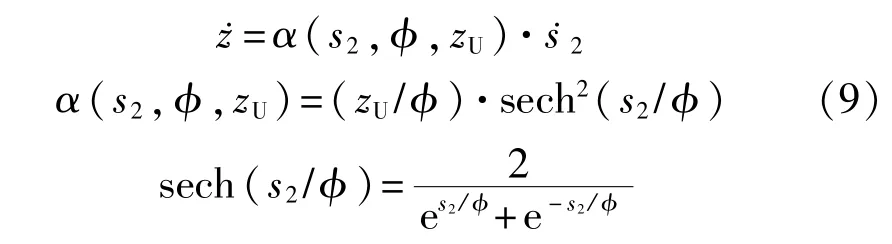
对式（8）求导，并由式（9）可得：

由等效控制法可得，系统在滑动面S上的等效控制为

定义系统的控制输入为

式中usw为系统的切换控制。

采用Lyapunov稳定性理论来求取系统的切换控制，选取Lyapunov函数：

对V求关于时间的导数，由式（10）～式（12）可以得到：

为确保系统的稳定性，令：

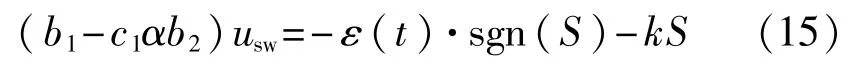
式中：k——正常数；

ε（t）——正的时变切换增益。由上式可得，系统的切换控制为

由式（16）可见，系统的抖振幅度由切换增益ε（t）来决定。为削弱滑模控制系统的抖振，本文采用等效控制关联增益法[13]来调节控制器的切换增益。定义时变切换增益ε（t）为

式中：ε0——正常数；

η={sgn（S）}eq——sgn（S）经低通滤波后得到

的平均值。

式中σ为滤波时间常数。

由式（11）和式（16）可得，系统的控制输入为

由式（15）可见，与文献[13]采用的等效控制关联增益法相比，本文设计的控制律中增加了控制项-kS。由式（17）可知，系统的抖振幅度正比于增益ε0。因此在控制律式（19）中，选取较大的增益k和较小的增益ε0，有利于实现系统的快速趋近并削弱系统的抖振。

3 稳定性分析

定理1：对于式（2）所示的桥式吊车系统，如果分别按式（5）、式（6）和式（8）设计系统的各层滑动面，并且采用式（19）所示的滑模控制律，那么系统的第二层滑动面S是渐近稳定的。

证明：将式（16）代入式（14），可以得到：

积分式（20），可以得到：

由上式进一步可得：

由式（17）和式（18）可知ε（t）∈L∞，又由式（22）可知S∈L∞，进而由式（20）可知从而有又由式（23）可知S∈L1，S∈L2，因此根据Barbalat引理[14]有

定理2：对于式（2）所示的桥式吊车系统，如果分别按式（5）、式（6）和式（8）设计系统的各层滑动面，并且采用式（19）所示的滑模控制律，那么系统的第一层滑动面s1和s2都是渐近稳定的。

对上式求导，可以得到：

由式（4）和式（6），可以得到：

由于参数zU的大小并不影响整个系统的稳定性，因此可以构造2个不同的滑动面：

式中zU1和zU2为任意小于1且不相等的正常数。不失一般性，这里进一步假设：

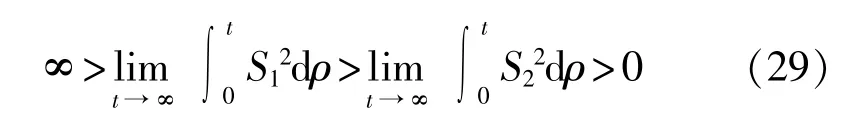
由式（28）和式（29），可以得到：

定理1中已经证明S1∈L1，从而由上式进一步可得：

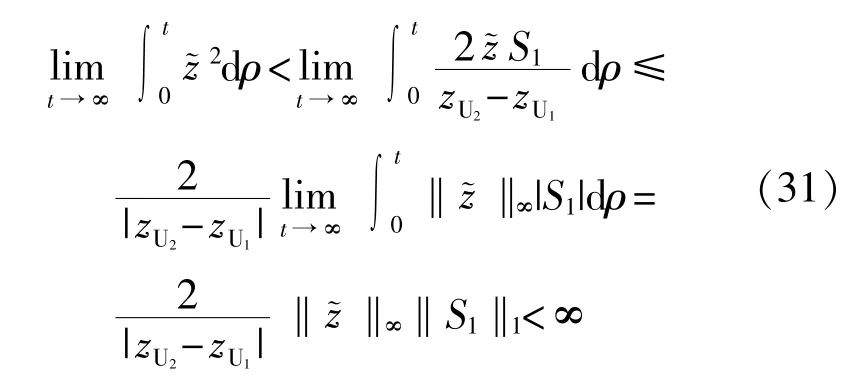
4 仿真验证

为验证本文提出的控制方法的有效性，在Matlab环境下进行数值仿真实验。仿真中，桥式吊车系统的各参数按文献[9]分别取：M=1 kg，m=0.8 kg，l=0.305 m，g=9.8m/s2。设系统的初始状态：x0=0，θ0=0，设台车的目标位置：xd=1m。本文设计的控制器各参数分别取：c1=0.63，c2=3.9，zU=0.79，φ=0.35，ε0=0.1，σ=0.02，k=9.8。

本文提出的控制方法的仿真实验结果如图2～图4所示。图2为台车位移和负载摆角的变化曲线，可以看出，在本文设计的控制器作用下系统的稳定时间为4.7s。具体而言，台车在4.7s已无超调地到达了目标位置，并且在4.5s实现了负载的抗摆控制，最大负载摆角为0.09rad。图3为控制输入的变化曲线，可以看出控制器只有很小幅度的抖振。图4为各层滑动面的收敛曲线，可以看出各层滑动面均能快速地趋近于0。

为进一步检验本文提出的控制方法的控制性能，选取文献[2]提出的控制方法与其进行对比分析。文献[2]设计的控制器各参数分别取：η1=0.05，α1=0.01，η2=0.02，α2=0.01。

文献[2]提出的控制方法的控制效果如图5所示，可以看出，在文献[2]设计的控制器作用下系统的稳定时间为5.7s。具体而言，台车到达目标位置的时间为4.3s，实现抗摆控制的时间为5.7s，最大负载摆角为0.12rad。由此可见，与文献[2]提出的控制方法相比，本文提出的控制方法在实现系统快速稳定和抑制负载摆动方面均显示出优越性。

为进一步检验本文提出的控制方法的抖振抑制特性，选取文献[10]提出的传统解耦滑模控制方法与其进行对比分析。文献[10]设计的控制器各参数分别取：λ1=0.74，λ2=4，Gf2=0.92，Gs2=1.8，Gf1=0.75。

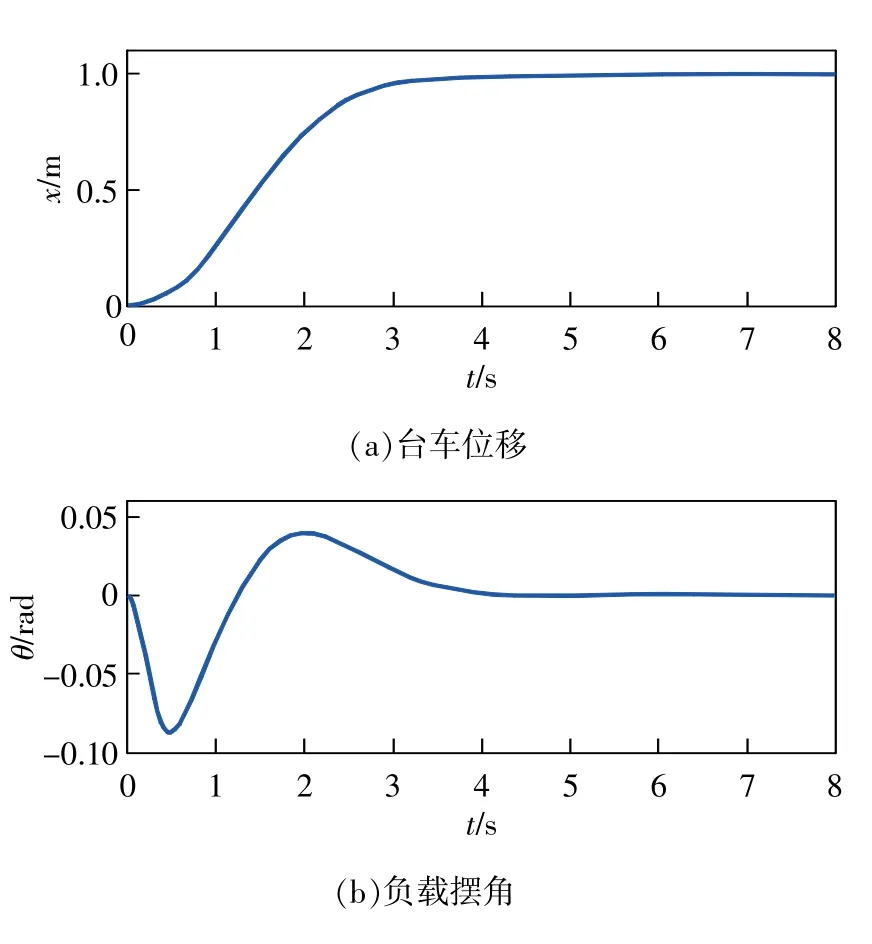
图2 台车位移和负载摆角的变化曲线

图3 控制输入的变化曲线

图4 系统各层滑动面的收敛曲线

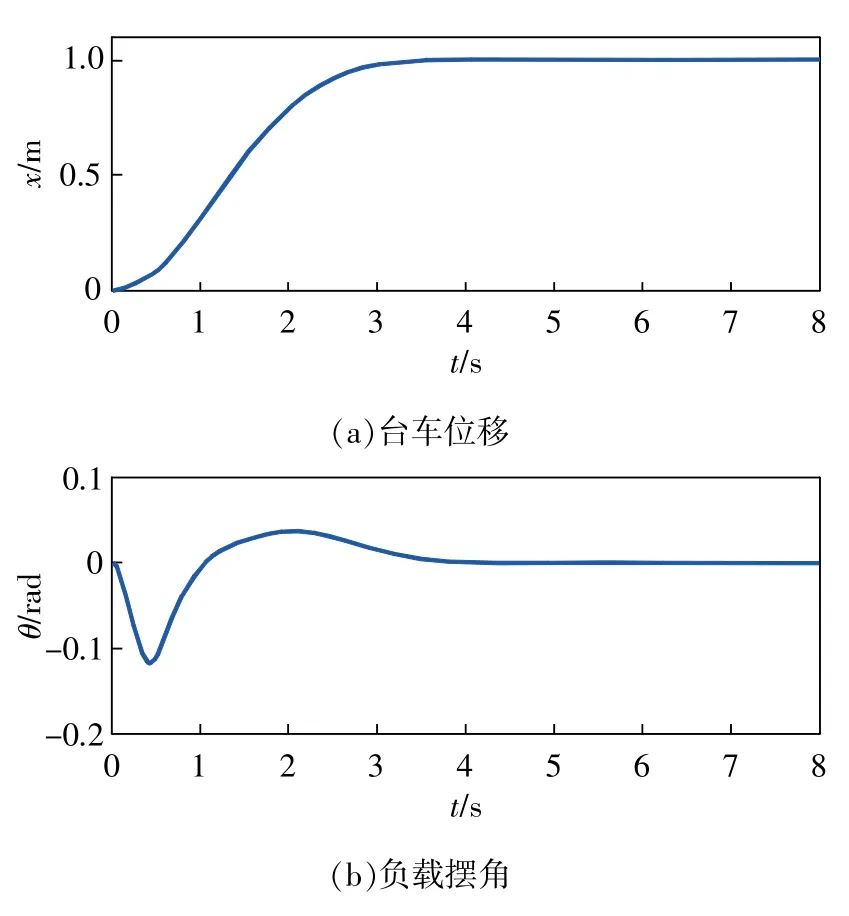
图5 文献［2］提出的控制方法的仿真结果

文献[10]提出的控制方法的控制效果如图6所示。由图6（a）和图6（b）可以看出，在文献[10]设计的控制器作用下系统的稳定时间为5.2s。具体而言，台车到达目标位置的时间为3.9s，完成抗摆动作的时间为5.2s，最大负载摆角为0.1rad。由此可见，本文提出的控制方法在实现系统快速稳定和抑制负载摆动方面均优于文献[10]提出的控制方法。进一步对比图6（c）和图3可以看出，虽然本文设计的控制器仍然存在很小幅度的抖振，但与文献[10]设计的控制器相比，本文提出的控制方法显著地降低了滑模控制系统的抖振幅度。

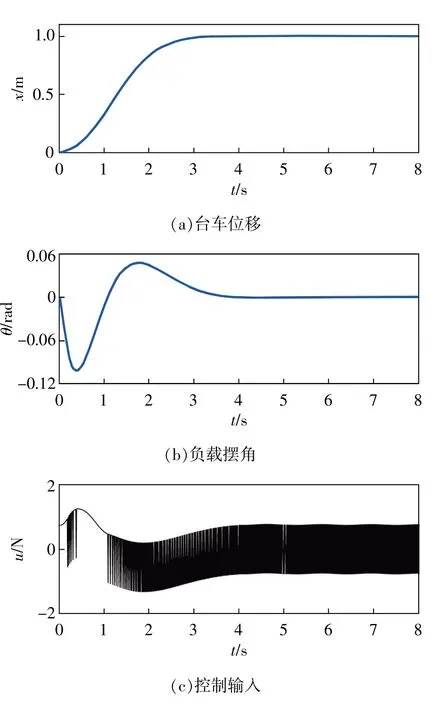
图6 文献［10］提出的控制方法的仿真结果

5 结束语

本文研究了欠驱动桥式吊车系统的抗摆控制问题，提出了一种具有时变切换增益的解耦滑模控制方法。通过引入可导的双曲正切函数型中间变量，该控制方法从本质上避免了传统解耦滑模控制中等效控制不能求取的问题。针对变结构控制系统的抖振问题，该控制方法采用了等效控制关联增益法来调节控制器中的时变切换增益。仿真实验结果不仅验证了理论分析的正确性和所提出的控制方法的有效性，并且表明该控制方法具有良好的控制性能和抖振抑制特性。此外，本文所提出的控制方法也为高阶欠驱动机械系统的控制提供了一种有效和可行的解决方案。

[1]LE A T，KIM G H，KIM M Y，et al.Partial feedback linearization control of overhead cranes with varying cable lengths[J].InternationalJournal of Precision Engineering and Manufacturing，2012，13（4）：501-507.

[2]李众峰，徐为民，谭莹莹，等.欠驱动桥式吊车自适应PID控制[J].计算机测量与控制，2013，21（6）：1522-1524.

[3]SUN N，FANG Y，ZHANG X.Energy coupling output feedback control of 4-DOF underactuated cranes with saturated inputs[J].Automatica，2013，49（5）：1318-1325.

[4]栗三一，余发山，卜旭辉，等.桥式起重机位置跟踪及防摆的迭代学习控制[J].电子测量与仪器学报，2014，28（2）：184-191.

[5]胡洲，王志胜，甄子洋.带输入饱和的欠驱动吊车非线性信息融合控制[J].自动化学报，2014，40（7）：1522-1527.

[6]孙宁，方勇纯，陈鹤.欠驱动桥式吊车消摆跟踪控制[J].控制理论与应用，2015，32（3）：326-333.

[7]SMOCZEK J.Evolutionary optimization of interval mathematics-based design of a TSK fuzzy controller for antiswaycranecontrol[J].International Journal of Applied Mathematics and Computer Science，2013，23（4）：749-759.

[8]RANJBARI L，SHIRDEL A H，ASLAHI-SHAHRI M，et al.Designing precision fuzzy controller for load swing of an overhead crane[J].Neural Computing and Applications，2015，26（7）：1555-1560.

[9]王伟，易建强，赵冬斌，等.基于稳定性分析的一类欠驱动系统的滑模控制器设计[J].信息与控制，2005，34（2）：232-235.

[10]MAHMOODABADI M J，MOSTAGHIM S A，BAGHERI A，et al.Pareto optimal design of the decoupled sliding mode controller for an inverted pendulum system and its stability simulation via Java programming[J].Mathematical and Computer Modeling，2013，57（5/6）：1070-1082.

[11]MAHMOODABADI M J，MOMENNEJAD S，BAGHERI A.Online optimal decoupled sliding mode control based on moving least squares and particle swarm optimization[J].Information Sciences，2014，268（6）：342-356.

[12]韩京元，田彦涛，孔英秀，等.板球系统自适应解耦滑模控制[J].吉林大学学报（工学版），2014，44（3）：718-725.

[13]LEE H.Chattering suppression in sliding mode control system[D].Columbus：The Ohio State University，2007.

[14]韩正之，陈彭年，陈树中.自适应控制[M].北京：清华大学出版社，2011：21-27.

（编辑：商丹丹）

Anti-sway control of overhead crane system based on decoupled sliding mode control

YU Tao1，YANG Kun1，ZHAO Wei2
（1.College of Mechanical Engineering and Automation，Liaoning University of Technology，Jinzhou 121001，China；2.School of Information Engineering，Beijing Institute of Graphic Communication，Beijing 102600，China）

A novel decoupled sliding mode control algorithm is proposed for anti-sway control of an underactuated overhead crane system.Different from traditional decoupled sliding mode control algorithm，the proposed control algorithm uses a differentiable intermediate variable to define the second-layer sliding surface of the system and utilizes the equivalent-control-dependent gain method to adjust the switching gain of the decoupled sliding mode controller.This algorithm can not only solve the derivation problem of the equivalent control of the decoupled sliding mode controller，but also reduce the chattering level of the decoupled sliding mode controller effectively.The asymptotic stability of sliding surface at each layer is proven by applying Lyapunov method and Barbalat's lemma，and numerical simulation results are provided to demonstrate the validity of the proposed control algorithm.Compared with the existing control algorithms，the results show that the proposed control algorithm has better control performance and chattering suppression characteristic.

overhead crane；underactuated；anti-sway control；decoupled sliding mode control

A

1674-5124（2017）08-0095-06

2016-12-10；

2017-02-05

辽宁省自然科学基金指导计划项目（201602379）；辽宁省教育厅科学技术研究一般项目（L2015241）

于涛（1980-），男，天津市人，讲师，博士，研究方向为机器人运动分析与控制、滑模控制理论与应用。

10.11857/j.issn.1674-5124.2017.08.020