基于数据融合的脉冲涡流厚度测量方法

张绍旺，黄坚，宋学青，马建民，殷春，田露露

（1.云南省计量测试技术研究院，云南昆明650228；2.电子科技大学自动化工程学院，四川成都611731）

基于数据融合的脉冲涡流厚度测量方法

张绍旺1，黄坚1，宋学青1，马建民1，殷春2，田露露2

（1.云南省计量测试技术研究院，云南昆明650228；2.电子科技大学自动化工程学院，四川成都611731）

在脉冲涡流检测中，通常使用响应信号的特征值，如峰值时间、峰值等来测量材料的厚度或缺陷的深度。该文提出一种新的测量方法对几何参数和材料电磁参数进行分离，实现厚度的测量。把被测对象的厚度被划分为一系列的标准厚度，每累加一次厚度，就会有一个对应频率的激励信号。由于脉冲激励信号拥有丰富的频率信号，可以用来作为厚度的扫描信号。通过对这些信号的分析，当扫描信号对应的厚度大于等于被测厚度时，该信号和参考值有很大区别，可以进行厚度测量。另外，为提高检测精度，引入数据融合的方法来综合数据信息，从而提高方法性能。

脉冲涡流；厚度测量；无损检测；数据融合

0 引言

目前，越来越多的学者对脉冲涡流无损检测技术进行研究，主要用于探测、定位和描述金属材料内部的缺陷[1-5]。其中脉冲涡流检测（pulsed eddy current testing，PECT）应用于缺陷检测，材料属性检测以及缺陷重构[6-8]。在产业中为了安全以及经济环保，会使用脉冲涡流厚度检测技术对一些复杂或大型设备如核电站和火力发电站等进行持续定期的检查，防止一些潜在的危险发生[9-10]。

目前，已经有很多学者在金属板厚度测量方面做了研究。据研究发现，很多研究方法都需要经过以下步骤：1）需要对很多同材料不同厚度的金属样板进行测量实验；2）使用一种响应曲线特征来描述或刻画不同的厚度；3）通过有限个特征点描绘一个拟合曲线来进行厚度拟合测量。这种一般的测量方法是一种非常耗时的研究过程，因为它需要对很多参考样件进行大量的测量实验。

本文提出一种基于数据融合方式的厚度测量方法，只需要一种参考样件和一个标准厚度的样件进行一次测量，就可以对同一种材料的不同进行测量。利用硬件的高速性可以一次采集多个信号，运用数据融合算法提高测量算法的精度。

1 电磁分析与数据融合方法

1.1 电磁理论分析

涡流的趋肤效应是涡流检测技术的理论基础，趋肤厚度[11]描述为

式中：δ——趋肤深度；

f——单频激励频率；

σ——电导率；

μ——磁导率。

图1为趋肤效应的示意图，当涡流越趋近与材料表面时，涡流密度会越来越大。

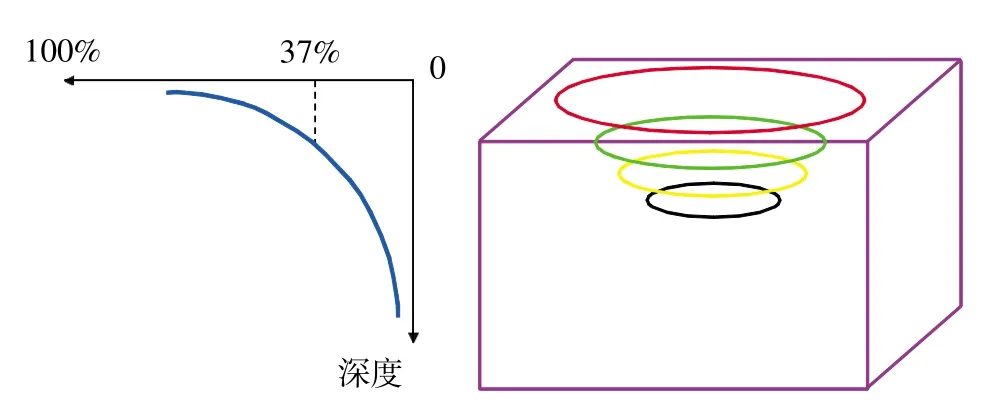
图1 涡流的趋肤效应

图2 涡流检测探头原理示意图

图2为涡流检测探头原理示意图。当对线圈通交变电流I1时，可以感生出交变磁场B1。由麦克斯韦理论知，在导体内部就可以产生涡流I2。

如果加载的激励频率足够高，使得其趋肤深度小于被测试件的厚度，那么对于在被测试件和参考试件中产生的涡流分布就会是一样的（参考试件厚度比任意被测试件都厚），如图3所示。其中试件a为被测试件，厚度为ta，试件b为参考试件，厚度为tb，且tb＞ta。

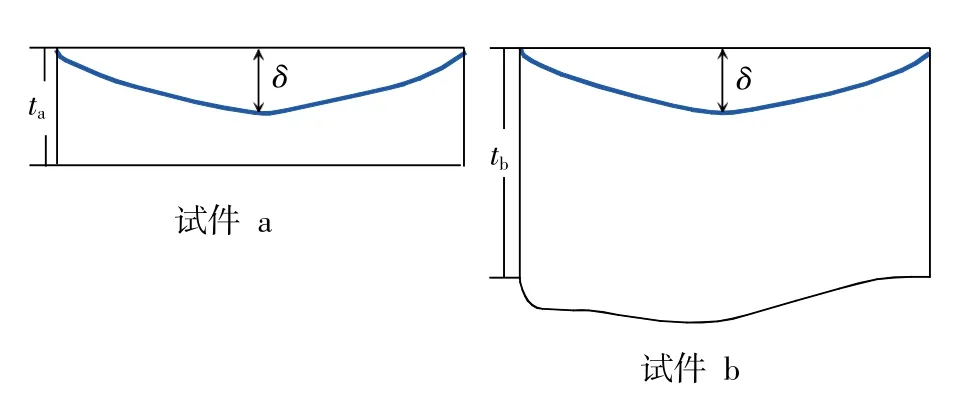
图3 不同厚度的趋肤效应对比

另一方面，趋肤深度δ会随着加载激励信号频率的降低而增大，当大于被测试件的厚度时（如ta），此时由试件a和b产生的感应磁场信号会发生改变。特别的是当刚好大于或等于被测厚度时，认为趋肤深度和ta相等。因此可以利用这个特征来计算和测量金属板的厚度。

根据趋肤效应式（1）可得到等式（2）：

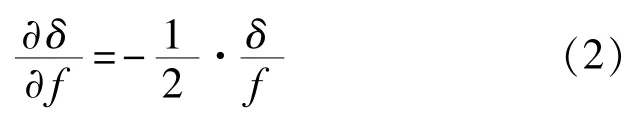
因此，对于每次厚度值可以根据下式描述：

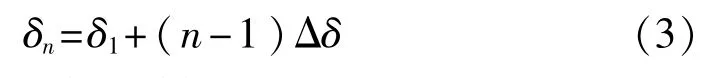
式中：δn——第n次趋肤深度；

δ1——初值；

n——自然数。

因此，对应于δn的激励频率为

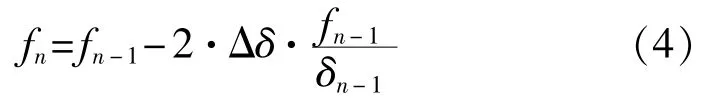
其中fn是第n个厚度所需要的激励频率。

根据式（3）和式（4）可以得到激励频率的一个通项关系：

为了可以准确地测量厚度，这里设定扫描步长为0.01mm，同时初始频率为f1。将扫描步长和初始频率带入式（5）式可以得到：

其中的初始化值δ1和f1可以通过测量一个标准的厚度试件获得。因此，在扫描过程中，激励频率需要按照式（6）的法则进行变化，通过这样规律的变化递减频率，可以使得测量厚度按照设定的厚度测量步长Δδ进行逐级增大直到测量到被测试件的厚度，且不确定度为±Δδ。

本文所研究的测量对象为PECT系统，根据Xie及其团队研究发现，PECT系统是一个线性系统，其响应信号可以认为是多种单频信号响应的叠加[12]。为了进一步提高精度，使用曲线拟合的方式将这一系列的离散点转换成连续的，如图4所示[13]，且能够有显式方程描述，其通式为

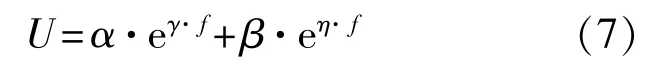
式中：U——拟合后的曲线函数；

α、β、γ、η——拟合参数；

e——自然底数；

f——频率。

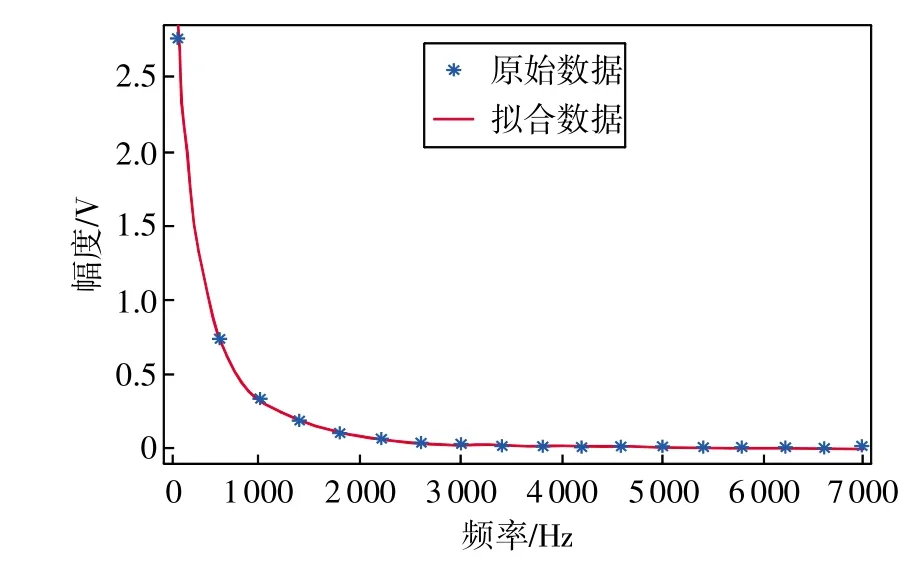
图4 拟合曲线

在实际研究中，检测信号是感应磁场，为了计算这个临界频率点，定义如下磁场变换关系：

式中：ΔB——涡流感生出的磁场信号；

Bref——测量参考试件（试件b）的值；

B——测量值（对应试件a）。

如果ΔB在频率fc处的值为零，定义该频率为扫描停止频率。将该频率带入式（6），可以得到扫描得到的频率对应的编号n。再通过式（3）则可以算出此时的厚度值，即试件的厚度。

1.2 数据融合方法

数据融合即采用一种方法，将多个数据进行融合，得到数据中差异或共性特征的方法。本文中的数据融合方法是建立在主成分分析（principal component analysis，PCA）方法之上的融合方法。

首先，PCA使用通过线性变换达到数据降维的算法，如下式所示：

其中X为多元变量，Xi为随机变量，Y是变换后得到的随机变量，Ω是线性变换矩阵。线性变换矩阵公式为

其中Var（*）表示计算方差。

实际上，线性变换矩阵是由矩阵X的特征向量所组成的，且按照特征值从大到小的顺序排列，即特征向量为γ1，γ2，···，γp，对应的特征值满足λ1＞λ2＞···＞λp。由此，第一主成分为γ1TX，γ2TX则为第二主成分，以此类推。

假设Xi是系统检测到的信号，i表示为第i次检测到的信号。由此多元随机变量可描述为下式：

将以上检测到的测量信号集合X带入到PCA算法中，就可以得到一个p维向量集合，如下式所示：

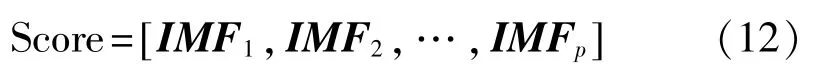
其中IMFi为第i模态分量，即第i个主成分数据。第一模态分量的贡献值高达99%，由此，IMF1可以用来代替检测到的数组集合X。

2 实验平台搭建

PECT测试平台主要包括脉冲信号激励源系统、检测探头1个（包括激励线圈和霍尔传感器）、三维定位平台和PC机。实验使用的平台如图5（a）所示。为了检测到PEC响应信号，在激励探头底部安装了一个霍尔传感器，其结构如图5（b）所示。由于三维位移平台的驱动，探头会在试件上移动。霍尔传感器紧贴着样件，采集到的涡流感应磁场即为检测信号。

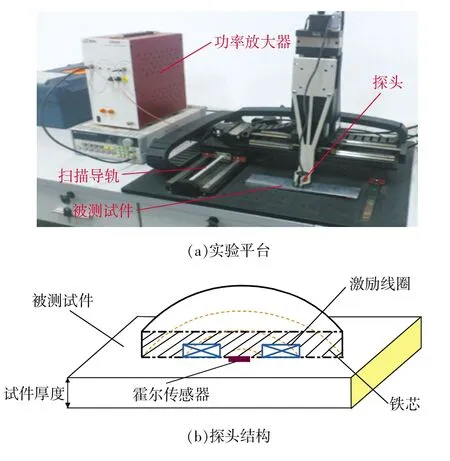
图5 PECT系统的实验平台和探头结构

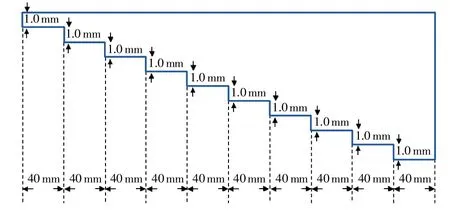
图6 样件示意图

实验中使用的样件如图6所示。其中有10个阶梯型的厚度，分别是总厚度的100%、90%、80%、70%、60%、50%、40%、30%、20%、10%，总厚度为10mm。

3 结果分析

图7为原始数据和融合数据的全貌图及细节图，可以清楚看到，对同一个厚度检测时，信号都会存在不同程度的差异。融合后的数据位置处于所有检测数据的靠近中间位置。对于不同信号产生的差异进行了特征提取，达到了滤波的效果。

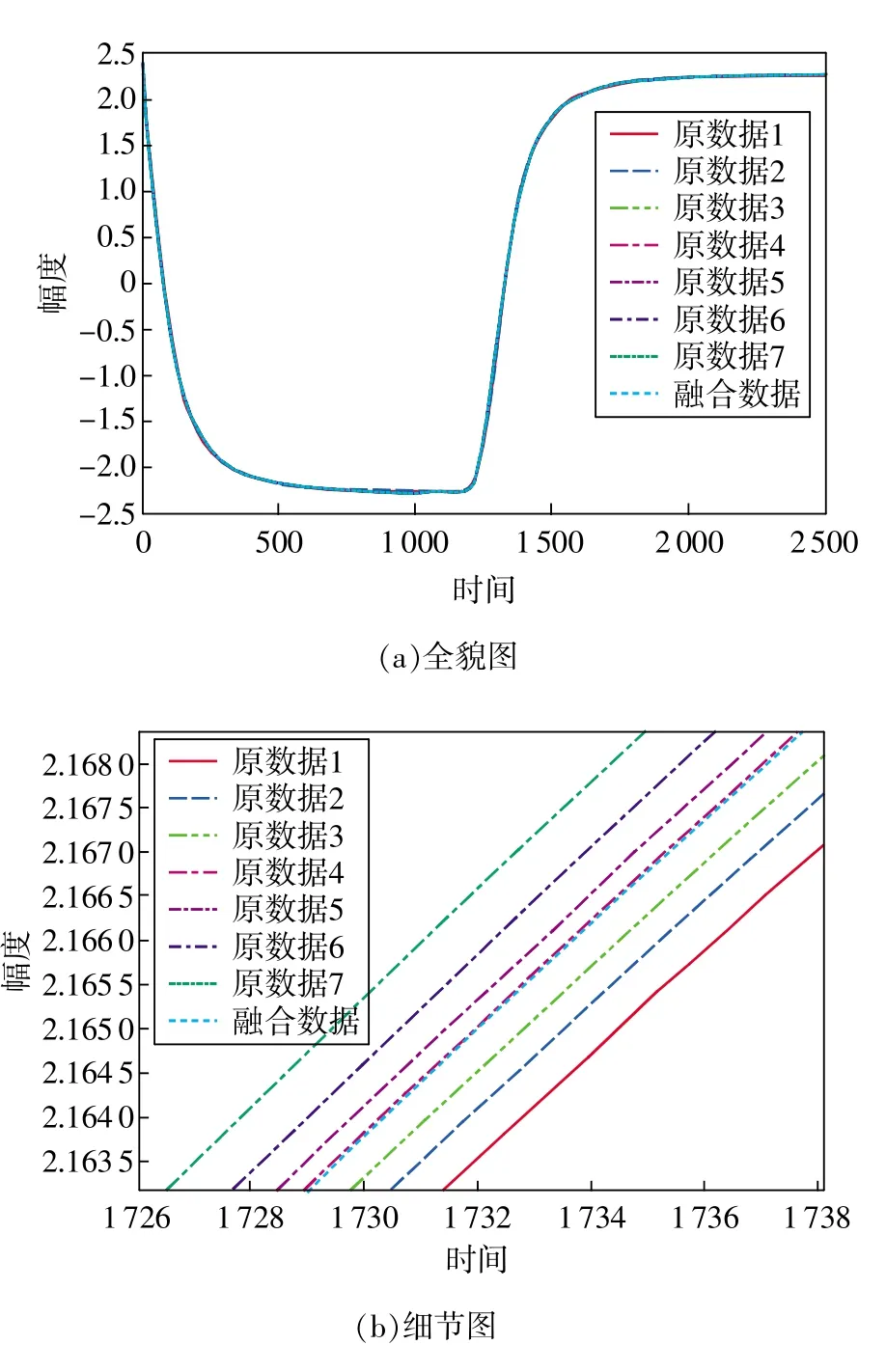
图7 原始数据和融合数据全貌及细节图

在本设计中，激励信号为200 Hz的方波，前端使用了一个2kHz的低通滤波器，因此ΔB（f）测量值有效的区间为FFT变换后的频率值在200～2000Hz之间。对于不同的厚度，ΔB（f）在不同频率时的值不同，如图8所示。

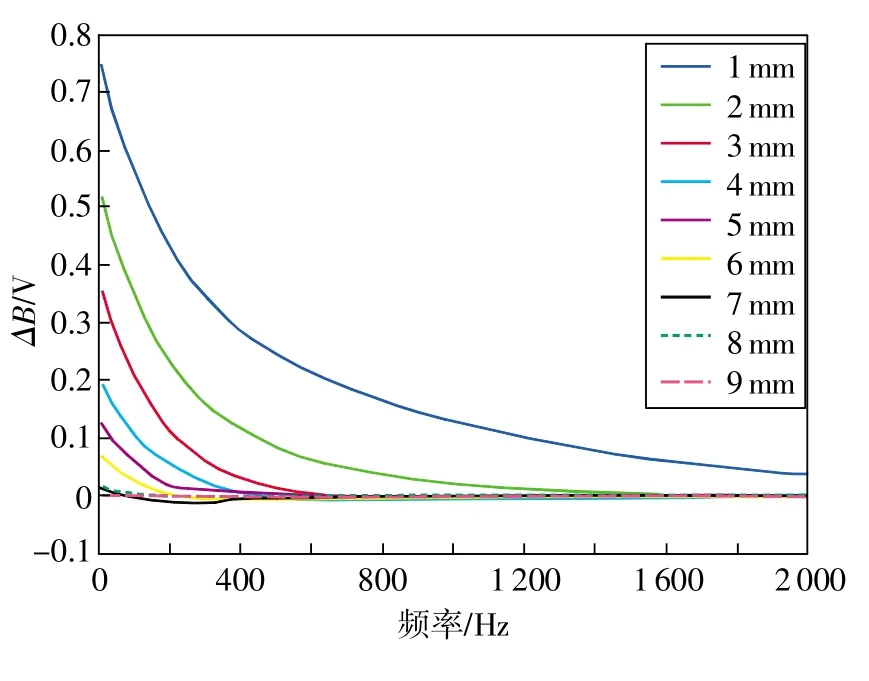
图8 ΔB与频率之间的关系

由于系统硬件会自动的把2000Hz以上的频率成分滤去，因此算法中的初始化值δ1和f1为测量2mm标准试件时获得。当δ1为2mm时，f1为1.610 kHz。为了使测量不确定度为0.2mm，取Δδ=0.01mm。

图9展示了算法在运算过程中扫描次数和收索到的特定厚度的频率关系。由图可知，对于薄厚度的试件，收索步数很少。

图9 扫描次数与频率之间的关系

表1为对不同厚度进行测量的结果。表中结果显示，测量结果的测量误差在0.04mm左右。需要注意的是，由于系统截止频率的原因，7，8，9mm没有被测量。

表1 测量结果

图10展示了每一个厚度所对应的畸变频率。可以看出，在测量1 mm厚度时，畸变频率被截止在了2kHz，这是由于算法自动筛选的结果。若希望测量1mm以下的厚度，需要提供2000Hz以上的频率激励。另一方面，厚度大于6mm时，所需的激励频率低于200Hz，这些都是系统认为不合理的。因此，在本次研究中，该系统可以在2～6mm厚度内进行有效地测量，其实测曲线与参考曲线拟合地很好。

图10 不同厚度下畸变频率

图11为测量值和参考值的对比图。可以看出，其最大误差为0.07mm，远小于设定的误差（0.2mm）。

图11 测量值和参考值的对比

结果显示，测量精度可以根据扫描步长Δδ来确定。同时，在计算中，所有的测量值都是以初始值为基准，因此选择初始值非常重要。本方法的提出可以增加整个系统的工作效率，并且不需要测量被测件的电磁参数值，简化了测量过程。

4 结束语

在本文中，一种基于数据融合的PECT测量系统的厚度测量方法被提出。该方法将被测试件厚度分为诺干个设定厚度，每个厚度的叠加都对应一个特定的频率。根据FFT变换，一系列的激励信号可以有效地被提取出来，每一个特定的频率对应的趋肤深度都可以是设定步长的整数倍，根据这个关系可以由步长Δδ计算出厚度值；同时测量厚度的精度可以根据步长来描述，这样可以使得精度可控，达到高精度测量。

[1]TIAN G Y，LI Y，MANDACHE C.Study of lift-off invariance for pulsed eddy-current signals[J].IEEE Transactions on Magnetics，2009，45（1）：184-191.

[2]PREDA G，HANTILA F I.Nonlinear integral formulation and neural network-based solution for reconstruction of deep defects with pulse eddy currents[J].IEEE Transactions on Magnetics，2014，50（2）：113-116.

[3]关佳.基于脉冲涡流无损检测方法的结构缺陷识别实验研究[D].成都：电子科技大学，2013.

[4]杨宾峰.脉冲涡流无损检测若干关键技术研究[D].长沙：国防科学技术大学，2006.

[5]PARK D G，ANGANI C S，RAO B P C，et al.Detection of the subsurface cracks in a stainless steel plate using pulsed eddy current[J].Journal of Nondestructive Evaluation，2013，32（4）：350-353.

[6]杨宾峰，罗飞路，曹雄恒，等.飞机结构腐蚀检测中的脉冲涡流无损检测技术[J].测试技术学报，2005（1）：27-29.

[7]周德强，吴佳龙，王俊，等.碳纤维增强复合材料冲击缺陷脉冲涡流无损检测仿真与试验研究[J].传感技术学报,2015，28（5）：671-676.

[8]ABIDIN I Z，TIAN G Y，WILSONJ，et al.Quantitative evaluation of angular defects by pulsed eddy current thermography[J].NDT&E International，2010，43（7）：537-546.

[9]KIM J W，LEE S H，PARK C Y.Experimental evaluation of the effect of local wall thinning on the failure pressure of elbows[J].Nuclear Engineering&Design，2009，239（12）：2737-2746.

[10]王三胜，易忠，侯化安，等.脉冲涡流无损检测技术及其用于航空航天材料缺陷检测的研究进展[J].航天器环境工程，2015，32（3）：307-312.

[11]KRAUSE H J，KREUTZBRUCK M V.Recent developments in SQUID NDE[J].Physica C&Its Applications Superconductivity，2002，368（1）：70-79.

[12]XIE S，CHEN Z，TAKAGI T，et al.Efficient numerical solver for simulation of pulsed eddy-current testing signals[J].IEEE Transactions on Magnetics，2011，47（11）：4582-4591.

[13]TIAN S，CHEN K，BAI L，et al.Frequency feature based quantification of defect depth and thickness[J].Review of Scientific Instruments，2014，85（6）：910-917.

（编辑：李刚）

Data fusion and pulsed eddy current method based for measuring the thickness

ZHANG Shaowang1，HUANG Jian1，SONG Xueqing1，MA Jianmin1，YIN Chun2，TIAN Lulu2
（1.Yunnan Institute of Measuring and Testing Technology，Kunming 650228，China；2.School of Automation Engineering，University of Electronic Science and Technology of China，Chengdu 611731，China）

Many features,just like the time of peak and peak value,of eddy current response signal are used to detect the specimen thickness or crack in pulsed eddy current testing.In this paper,it proposed a new thickness measuring method to separate the geometrical parameters and electromagnetic parameters.In the research,the thick of the specimen is broken into a series of unit thick and the excited signal would be control when the measuring thickness added one unit thick.As the pulsed eddy current signal has rich of frequency components,they could be used as the scanning signal of corresponding thickness.By analyzing the response signal,when the thickness that should be measured is bigger than the thickness that the scanning signal is corresponded,the scanning signal is very different to the reference signal.It can be utilized to measure the thickness by using the difference information.In order to improve the detection accuracy,it imported a data fusion method to combine the data information.By using the data fusion method,the property of this eddy current based thickness measuring method is increased deeply.

pulsed eddy current（PEC）；thickness measuring；nondestructive testing；data fusion

A

1674-5124（2017）08-0028-05

2017-04-12；

2017-05-25

张绍旺（1964-），男，云南曲靖市人，高级工程师，硕士，主要从事计量管理及测量技术研究。

10.11857/j.issn.1674-5124.2017.08.007