冬枣压缩特性实验与计算仿真研究
彭俊,谢洪起,冯亚利,傅隆生,2,*,VÁZQUEZ-ARELLANO Manuel,李 瑞
(1.西北农林科技大学机械与电子工程学院,陕西 杨凌 712100;2.农业部农业物联网重点实验室,陕西 杨凌 712100;
3.霍恩海姆大学农业工程研究所,德国 巴符 斯图加特 70599)
冬枣压缩特性实验与计算仿真研究
彭俊1,谢洪起1,冯亚利1,傅隆生1,2,*,VÁZQUEZ-ARELLANO Manuel3,李 瑞1
(1.西北农林科技大学机械与电子工程学院,陕西 杨凌 712100;2.农业部农业物联网重点实验室,陕西 杨凌 712100;
3.霍恩海姆大学农业工程研究所,德国 巴符 斯图加特 70599)
为了研究冬枣果实在收获、分选、运输及贮藏过程的力学特性,对冬枣果实进行压缩实验和有限元仿真,分析不同成熟度白熟期和脆熟期冬枣在不同压缩方向下的弹性模量以及接触应力。压缩实验结果表明:白熟果实的破裂力大于脆熟果实;二者的压缩曲线相似,横向压缩曲线有较明显的生物屈服点,纵向压缩时没有明显的屈服点。横向压缩时,白熟果实的平均弹性模量计算值与仿真值分别为3.527 MPa和3.263 MPa,平均误差为11.38%;脆熟果实的平均弹性模量计算值与仿真值分别为3.131 MPa和2.877 MPa,平均误差分别为12.96%。纵向压缩时,白熟和脆熟果实的弹性模量计算值与仿真值平均误差分别为26.24%和27.66%。压缩应力云图显示:上压头接触面的最大应力大于与固定底板接触面的最大应力;横向压缩时,上下表面的接触应力呈现对称分布;相同的压缩方向,白熟果实的计算最大应力和仿真最大应力都大于脆熟果实;最大应力的计算值和仿真值的误差较大,最小平均误差为26.24%。研究结果可为冬枣运输、分级及贮藏过程中选择合适的包装设计和摆放方式提供理论参考。
冬枣;压缩特性;弹性模量;有限元仿真
彭俊, 谢洪起, 冯亚利, 等. 冬枣压缩特性实验与计算仿真研究[J]. 食品科学, 2017, 38(17): 20-25. DOI:10.7506/ spkx1002-6630-201717004. http://www.spkx.net.cn
PENG Jun, XIE Hongqi, FENG Yali, et al. Experimental and simulation studies on mechanical properties of jujube (Zizyphus jujuba Mill. cv. Dongzao)[J]. Food Science, 2017, 38(17): 20-25. (in Chinese with English abstract) DOI:10.7506/spkx1002-6630-201717004. http://www.spkx.net.cn
枣(Zizyphus jujuba Mill.)为鼠李科枣属植物,是我国最古老的果树之一,已有3 000多年的栽培历史。枣树由于抗逆性强、早果速丰、营养丰富、经济和社会效益显著等特点而被广泛种植[1]。冬枣作为鲜食枣的一种,具有很高的营养价值,VC含量尤其丰富,有“百果之王”和“活维生素丸”的美誉[2]。
冬枣皮薄肉脆,在收获、运输及分选过程中,由于碰撞易产生机械损伤。随着我国农业劳动力转移加速,收获季节时雇工困难问题愈发突显,果实的机械化收获是发展趋势。但是,机械化收获不可避免会产生损伤,因此研究减少或避免机械损伤是有必要的。在类似研究中,需要首先解析果实的物理和生物力学特性。研究果实的生物力学特性,主要是运用压缩实验和力学计算方法,如对杨梅[3]、枣[4-6]、苹果[7-8]、苹果梨[9]、哈密瓜[10-11]、番茄[12-14]和荔枝[15]的压缩力学特性的研究;也采用有限元方法对番茄[16-19]、龙眼[20]、荔枝[21-22]、西瓜[23]、葡萄[24]、苹果[25-28]和咖啡[29]等进行力学特性研究。这些研究结果为如何减少果实在收获、加工、贮藏、包装和运输等过程中的机械损伤提供了理论依据。但对于冬枣目前鲜见相关报道。
本实验研究不同成熟期(白熟期和脆熟期)冬枣的弹性模量和压缩接触应力。利用压缩实验获得不同方向的力学特性曲线,运用理论计算和仿真分析的方法解析冬枣的弹性模量和压缩接触应力。通过理论计算值和仿真值对比,明确理论公式在冬枣果实压缩中的适用性和局限性,为在不同压缩类型下计算果实压缩特性提供一个参考方向。研究结果将为设计制造有关生产、加工和处理等机械设备提供理论参考,给冬枣收获力学模型的建立和有限元仿真提供参数来源。
1 材料与方法
1.1 材料
实验冬枣产自陕西省大荔县,共120 个样本,其中白熟期果实60 个(20 个购于2015年10月,编号为:B1~B20;40 个购于2016年10月,编号为:B21~B60)和脆熟期果实60个(20个购于2015年10月,编号为:C1~C20;40个购于2016年10月,编号为:C21~C60)。
1.2 仪器与设备
HY0580万能实验仪(最大压力为2 000 N,分辨率为0.001 N) 衡翼精密仪器有限公司;MakerBot Digitizer 3D扫描仪(精度±2 mm) 北京威控睿博科技有限公司。
1.3 方法
1.3.1 果实压缩实验
测量果实质量和尺寸,尺寸包括3 个方向:长(果蒂至花萼方向)、宽(果实赤道长轴方向)、厚(果实赤道短轴方向)。
压缩实验采用万能实验仪HY0580测定。果实压缩实验的压头采用刚性圆柱压头,下压板固定不动,上压头垂直向下平行压缩,下压速率为10 mm/min。压缩方向分为果实纵向压缩和横向压缩,即压缩果实的长度方向和宽度方向,其中样本B1~B10、B21~B40、C1~C10和C21~C40进行横向压缩,如图1a所示;样本B11~B20、B41~B60、C11~C20和C41~C60进行纵向压缩,如图1b所示。

图 1 冬枣的横向压缩和纵向压缩实验Fig. 1 Compression test in transverse and vertical directions
1.3.2 果实压缩的有限元仿真
果实压缩的有限元仿真采用ANSYS 15.0软件对果实的压缩过程进行模拟分析。首先运用3D扫描仪扫描果实的外形轮廓,生成果实表面点云,如图2a所示;再通过CATIA软件(V5-6R2014,Dassault Systemes S.A.)将点云转化为曲面,如图2b所示;最后由曲面生成实体模型,如图2c所示。
将三维实体模型导入有限元软件,生成有限元模型,按照真实压缩条件添加上、下压板。根据果实在压缩实验中所受的力和约束设置果实在仿真环境中的边界条件,果实与压板之间采用刚性表面接触,如图3所示。材料类型选用线弹性材料,材料属性中枣果密度用以上测量的数据,白熟果实的泊松比取0.394,脆熟果实的泊松比取0.383[30]。

图 2 枣3D模型创建过程Fig. 2 Procedure of creating a 3D digital model for jujube fruits

图 3 有限元模型压缩变形图Fig. 3 Deformation from fi nite element model
将仿真计算的数据与实际压缩的数据进行对比,当二者结果符合时,以仿真计算中输入的弹性模量为果实在压缩实验中的弹性模量。因此,弹性模量的计算与仿真步骤如下:1)测量样本基本物理参数,进行压缩实验并记录果实所受的力F以及果实的变形量δ;2)建立被压果实有限元模型,按照实验条件设置边界条件,弹性模量定义为EF运行计算得出果实的变形量δF;3)如δF>δ,则下次仿真的输入弹性模量E=EF+ΔE,其中ΔE根据δ、EF和δF定义为ΔE=|δ-δF|EF/nδF(n≥2);如δF<δ,则下次仿真的输入弹性模量为E=EF-ΔE;4)重复步骤3)直到δF=δ,则果实弹性模量E=EF。
2 结果与分析
2.1 枣果压缩曲线分析
白熟期和脆熟期的果实受到不同方向压力作用时,力与变形的曲线图如图4所示。生物屈服点是应力应变曲线中,应力开始较少或应变不再增加的点。由图4可知,白熟期和脆熟期的枣果纵向压缩曲线趋势相似,都无明显的生物屈服点(bioyield point)出现,当压力达到破裂点(rupture point)时果实发生破裂。横向压缩时曲线有较为明显的生物屈服点,该点之后的曲线比其之前的曲线变化较为平缓,当压力达到第2个峰值时果实破裂,白熟期果实破裂力要大于脆熟期果实破裂力。白熟果实在破裂点前的曲线近似直线,脆熟期果实在屈服点前的曲线近似直线。在弹性范围内,相同的作用力下,白熟期果实的变形要小于脆熟期果实的变形,即白熟期果实的刚度大于脆熟期果实。

图 4 冬枣果实压缩的力-变形图Fig. 4 Force-deformation curves of jujube fruits
2.2 果实压缩弹性模量与最大应力计算
由于枣果实形状不规则,在压缩过程中难以运用材料力学理论计算果实的应力和应变,不能直接获得果实的弹性模量。但可以通过其他接触理论计算得出,例如,付威等[5]根据布森聂接触理论计算骏枣和灰枣在压缩过程中的弹性模量,美国农业工程师协会(American Society of Agricultural Engineering,ASAE)的行业标准运用赫兹接触理论计算果实的压缩弹性模量和最大接触应力[31]。本实验将运用ASAE行业标准的方法计算果实弹性模量和最大应力。
果实压缩时,其赫兹接触半径可由果实接触点的曲率半径表示,横向压缩弹性模量通过式(1)计算出压缩弹性模量。压缩的最大接触应力发生在接触面的中心处,即果实与压板最先接触点处,由式(2)计算得出。
式中:E为压缩弹性模量/MPa;Smax为最大接触应力/MPa;F为作用力/g;v为泊松比;D为变形/mm;RUmin和RUmax分别为果实上表面的压缩接触点的最小和最大曲率半径/mm;RLmin和RLmax分别为果实下表面的压缩接触点的最小和最大曲率半径/mm;KU和KL是由上、下表面接触点的曲率半径决定的常数;C1和C2分别是与接触面积有关的常数,其数值根据cosθ的值查表1后线性差值得出,其中cosθ由式(3)确定。
式中:Rmin和Rmax分别是接触点的最小和最大曲率半径/mm。

表 1 KU、KL、C1、C2与cosθ值对应表Table 1 Values of KU, KL, C1and C2for various values of cosθ
由于扫描果实模型有很高的精度,故实际计算过程中,果实的上下接触点的曲率半径用扫描模型上对应的点的曲率半径代替。扫描模型上的接触点的曲率半径由CATIA软件中的曲率分析功能测量得出,其最大、最小曲率半径的测量如图5所示。

图 5 果实曲率半径测量Fig. 5 Measurement of curvature radius
2.3 果实压缩仿真数据分析
弹性模量是材料在弹性变形范围内应力与应变的比值,赫兹接触方程亦假定变形为小变形及材料在弹性范围内压缩,为了获得冬枣果实的弹性模量,故在果实弹性变形范围内进行研究。果实横压时,模拟载荷选择破裂点的载荷;果实竖压时,模拟载荷选择生物屈服点的载荷。

表 2 弹性模量的计算值与仿真值Table 2 Comparison of elastic moduli between simulation and calculation by the ASAE standard
如表2所示,横向压缩和纵向压缩时,白熟期果实的计算弹性模量和仿真弹性模量的均值都比脆熟期果实的大,与图4压缩曲线中得出的白熟果实刚度大于脆熟果实刚度的结论一致。由于果实成熟度越高,果实肉质越松软,果实刚度越小,研究结果表明果实越成熟,其压缩弹性模量越小。
横向压缩时,白熟期果实的弹性模量计算值与仿真值平均误差为11.38%,其中弹性模量计算均值为3.527 MPa,仿真均值为3.263 MPa。脆熟期果实的弹性模量计算值与仿真值的平均误差为12.96%,其中弹性模量计算均值为3.131 MPa,仿真均值为2.877 MPa。纵向压缩时,计算值与仿真值误差较大,白熟果实弹性模量计算值与仿真值平均误差为26.24%,脆熟果实的为27.66%,且纵向压缩弹性模量大于横向压缩弹性模量。产生误差的原因可能是:在弹性模量理论计算时,下底面接触点非单点接触,而是多点接触,甚至环形面接触,所以用ASAE标准的单点接触计算公式存在误差,导致在有限元分析过程中的接触面与理论计算的接触面不相符。

表 3 最大应力的仿真值与计算值Table 3 Comparison of maximum stress between simulation and calculation by the ASAE standard
果实的最大应力如表3所示,最大应力的计算值和仿真值的误差较大。横向压缩时,白熟果实的最大应力计算均值为0.822 MPa,最大应力仿真均值与计算均值误差为25.81%;脆熟果实的最大应力计算均值为0.947 MPa,最大应力仿真均值与计算均值误差为31.86%。
纵向压缩时,白熟果实最大应力计算值的均值为1.128 MPa,最大应力仿真均值与计算均值误差为42.14%。脆熟果实最大应力计算均值为1.042 MPa,最大应力仿真值与计算值误差为30.43%。相同的压缩方向,白熟果实计算最大应力和仿真最大应力都大于脆熟果实的最大应力。


图 6 果实B3横向压缩的应力云图Fig. 6 Von Mises stress contours of sample B3 under transverse compression
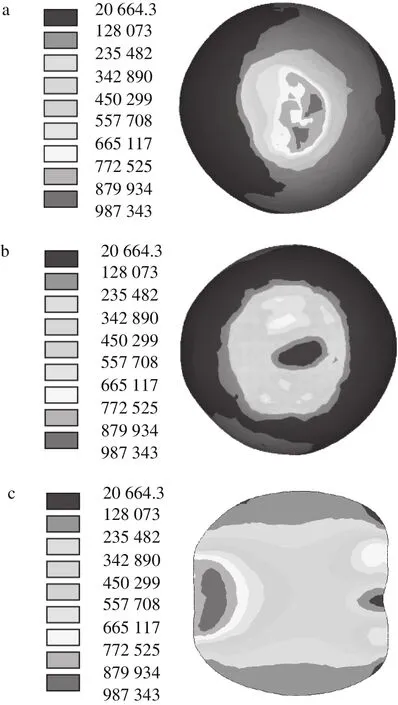

图 7 果实B14纵向压缩的应力云图Fig. 7 Von Mises stress contours of sample B14 under vertical compression
果实横向压缩和纵向压缩的应力云图如图6、7所示,果实上表面应力大于下表面应力,即与压头接触点应力大于与固定底板接触点应力,这与实验时果实在上压头处先破裂流出组织液的结果一致。横向压缩时,上下接触点的应力关于果实中心轴线对称分布。纵向压缩时,上下接触点的应力不呈现对称分布,最大应力出现在果蒂部位。
计算值与仿真值比较接近,因此在研究果实生物力学特性时,有限元仿真也是一种可采取的方法,相比传统力学实验和复杂的理论计算,模拟仿真更方便快捷。仿真结果可为果实收获,运输及包装提供数据参考。纵向压缩时的应力只集中出现在花萼处,果蒂处未出现应力集中,这可为减少包装和运输过程中的机械损伤提供依据。
3 结 论
白熟期果实和脆熟期果实在相同压缩方向的压缩曲线趋势相近,纵向压缩曲线没有明显的生物屈服点,横向压缩曲线有较为明显的生物屈服点。在弹性范围内,白熟期果实的刚度大于脆熟期果实的刚度。
果实横向压缩时,ASAE标准计算弹性模量值和仿真弹性模量值的平均误差较小;果实纵向压缩时,计算弹性模量值和仿真弹性模量值的平均误差较大。因此,计算果实的横向压缩弹性模量时,可采用ASAE标准;但在计算果实的纵向压缩弹性模量,采用ASAE标准时不能忽略果实果蒂部分的凹凸面。纵向压缩弹性模量大于横向压缩弹性模量,研究结果可为冬枣运输及贮藏过程中选择合适的包装条件和摆放方式提供参考依据。
上压头接触面的最大应力大于固定底板接触面的最大应力,横向压缩时,上下接触点的应力呈现对称分布。计算的最大应力值和仿真值的平均误差较大,故用ASAE标准预测凸面形状果实的最大接触应力有待进一步研究。
[1] 樊保国. 枣果的功能因子与保健食品的研究进展[J]. 食品科学, 2005, 26(9): 569-573.
[2] 武之新, 武婷. 冬枣优质丰产栽培新技术[M]. 北京: 金盾出版社, 2007: 1-7.
[3] 马晓丽, 陈晓英, 闫语丝, 等. 杨梅果的机械损伤试验和生物力学特性[J]. 农业工程学报, 2012, 28(16): 282-287.
[4] 王伟, 杨红英, 黄新成, 等. 红枣果肉力学特性试验研究[J]. 江苏农业科学, 2015, 43(6): 404-406.
[5] 付威, 何荣, 坎杂, 等. 红枣力学特性的试验研究[J]. 石河子大学学报: 自然科学版, 2013, 31(4): 518-522.
[6] LI R, PENG J, SUN S, et al. Determination of selected physical and mechanical properties of Chinese jujube fruit and seed[J]. Agricultural Engineering International: CIGR Journal, 2016, 18(3): 294-300.
[7] 李小昱, 王为. 苹果压缩特性的研究[J]. 西北农业大学学报, 1998, 26(2): 112-115.
[8] 姬伟, 李俊乐, 杨俊, 等. 机器手采摘苹果抓取损伤机理有限元分析及验证[J]. 农业工程学报, 2015, 31(5): 17-22.
[9] 杨晓清, 陈忠军, 朱丽静. 苹果梨静载机械特性的研究[J]. 食品科学, 2007, 28(8): 90-93.
[10] 杨晓清, 王春光. 河套蜜瓜机械特性与静载损伤关系的研究[J]. 农业工程学报, 2008, 24(3): 31-37.
[11] SEYEDABADI E, KHOJASTEHPOUR M, SADRNIA H. Predicting cantaloupe bruising using non-linear finite element method[J]. International Journal of Food Properties, 2015, 18(9): 2015-2025. DOI:10.1080/10942912.2014.951892.
[12] 王荣, 焦群英, 高永毅. 番茄力学特性的研究[J]. 农机化研究, 2003(4): 56-59.
[13] 李智国, 刘继展, 李萍萍. 机器人采摘中番茄力学特性与机械损伤的关系[J]. 农业工程学报, 2010, 26(5): 112-116.
[14] GLADYSZEWSKA B, CIUPAK A. Changes in the mechanical properties of the greenhouse tomato fruit skins during storage[J]. Technical Sciences, 2009, 12(2): 1-8.
[15] 陈燕, 蔡伟亮, 邹湘军, 等. 荔枝鲜果挤压力学特性[J]. 农业工程学报, 2011, 27(8): 360-364. DOI:10.3969/j.issn.1002-6819.2011.08.063.
[16] 吕胜权, 吴杰, 冯哲. 加工番茄静压内部应力的有限元分析[J]. 食品与机械, 2013, 29(5): 3-5.
[17] KABAS O, CELIK H K, OZMERZI A, et al. Drop test simulation of a sample tomato with fi nite element[J]. Journal of the Science of Food and Agriculture, 2008, 88(9): 1537-1541. DOI:10.1002/jsfa.3246.
[18] LI Z, WANG Y. A multiscale finite element model for mechanical response of tomato fruits[J]. Postharvest Biology and Technology, 2016, 121: 19-26. DOI:10.1016/j.postharvbio.2016.07.008.
[19] LI Z, LI P, YANG H, et al. Mechanical properties of tomato exocarp, mesocarp and locular gel tissues[J]. Journal of Food Engineering, 2012, 111(1): 82-91. DOI:10.1016/j.jfoodeng.2012.01.023.
[20] 卿艳梅, 李长友, 黄汉东, 等. 龙眼力学特性的有限元分析[J]. 农业机械学报, 2011, 42(6): 143-147.
[21] 陈燕, 蔡伟亮, 邹湘军, 等. 荔枝的力学特性测试及其有限元分析[J].农业工程学报, 2011, 27(12): 358-363.
[22] MARQUEZCARDOZO C J, CARTAGENAVALENZUELA J R, CIROVEL-SQUEZ H J. Physicochemical characteristics and finite element simulation of fi rmness in soursop fruits (Annona muricata L. cv. Elita) during postharvest[J]. Dyna, 2012, 79(172): 141-147.
[23] 王芳, 王春光, 杨晓清. 西瓜的力学特性及其有限元分析[J]. 农业工程学报, 2008, 24(11): 118-121.
[24] 王荣, 焦群英, 魏德强, 等. 葡萄的力学特性及有限元模拟[J]. 农业工程学报, 2005, 21(2): 7-10.
[25] AHMADI E, BARIKLOO H, KASHFI M. Viscoelastic fi nite element analysis of the dynamic behavior of apple under impact loading with regard to its different layers[J]. Computers and Electronics in Agriculture, 2016, 121: 1-11. DOI:10.1016/j.compag.2015.11.017.
[26] CELIK H K, RENNIE A E W, AKINCI I. Deformation behaviour simulation of an apple under drop case by fi nite element method[J]. Journal of Food Engineering, 2011, 104(2): 293-298. DOI:10.1016/ j.jfoodeng.2010.12.020.
[27] KIM G W, KIM M S, SAGARA Y, et al. Determination of the viscoelastic properties of apple fi esh under quasi-static compression based on finite element method optimization[J]. Food Science and Technology Research, 2008, 14(3): 221-231. DOI:10.3136/fstr.14.221.
[28] KIM G W, DO G S, BAE Y, et al. Analysis of mechanical properties of whole apple using fi nite element method based on three-dimensional real geometry[J]. Food Science and Technology Research, 2008, 14(4): 329-336. DOI:10.3136/fstr.14.329.
[29] TINOCO H A, OCAMPO D A, PENA F M, et al. Finite element modal analysis of the fruit-peduncle of Coffea arabica L. var. Colombia estimating its geometrical and mechanical properties[J]. Computers and Electronics in Agriculture, 2014, 108: 17-27. DOI:10.1016/j.compag.2014.06.011.
[30] JITPREEDAKORN R, BOONKRACHANG N, JARIMOPAS B. Mechanical properties of jujube as related to maturity[J]. Agricultural Science Journal, 2008, 39(3): 331-334.
[31] ASABE. Compression test of food materials of convex shape: S368.4 DEC2000 (R2008)[S]. 2008: 580-587.
Experimental and Simulation Studies on Mechanical Properties of Jujube (Zizyphus jujuba Mill. cv. Dongzao)
PENG Jun1, XIE Hongqi1, FENG Yali1, FU Longsheng1,2,*, VÁZQUEZ-ARELLANO Manuel3, LI Rui1
(1. College of Mechanical and Electronic Engineering, Northwest A & F University, Yangling 712100, China; 2. Key Laboratory of Agricultural Internet of Things, Ministry of Agriculture, Yangling 712100, China; 3. Institute of Agricultural Engineering, University of Hohenheim, Stuttgart 70599, Germany)
Compression test and fi nite element method (FEM) simulation were conducted to investigate the compression properties of jujube fruits (Zizyphus jujuba Mill. cv. Dongzao) at different ripening stages. The study aimed at reducing mechanical damage at harvest and during postharvest sorting, transportation and storage. The elastic moduli and contact stress of jujubes harvested at the white maturity and crisp maturity stages were measured under compression in two directions. From the experiment data, it was observed that the rupture force of white maturity fruits was greater than that of crisp maturity fruits in both transverse and vertical compression directions. The force-deformation curves of white maturity and crisp maturity fruits were similar, with obvious bioyield point under transverse compression rather than under vertical compression. Under transverse compression, elastic modulus predicted by the standard established by the American Society of Agricultural Engineering (ASAE) was in agreement with that evaluated by FEM simulation. The average apparent elastic modulus of white maturity fruits predicted by the ASAE standard and evaluated by FEM simulation were 3.527 and 3.263 MPa, respectively with an average relative difference of 11.38%, while those of crisp maturity fruits predicted by the ASAE standard and evaluated by FEM simulation were 3.131 and 2.877 MPa, respectively with an average relative difference of 12.96%. However, there was a larger difference between the elastic modulus predicted by the ASAE standard and that determined through FEM simulation under vertical compression, which was 26.24% and 27.66% for white and crisp maturity fruits, respectively. These results can provide a theoretical basis for packaging design and stacking for transportation, grading and storage.
Dongzao jujube; compression properties; elastic modulus; fi nite element method
10.7506/spkx1002-6630-201717004
TS255
A
1002-6630(2017)17-0020-06引文格式:
2016-07-02
国家自然科学基金青年科学基金项目(31301242);中国博士后科学基金项目(2015M572602);陕西省重点研发计划一般项目-农业领域(2017NY-164);西北农林科技大学国际科技合作种子基金项目(A213021505)
彭俊(1991—),男,硕士研究生,研究方向为果实的生物力学特性及其应用。E-mail:jxpengjun@nwafu.edu.cn *通信作者:傅隆生(1984—),男,副教授,博士,研究方向为农业智能化技术与装备。E-mail:fulsh@nwafu.edu.cn

