低速长航时无人机垂直突风过载分析
李建华,刘凯,李平坤,李锋
(中国航天空气动力技术研究院 彩虹无人机科技有限公司,北京 100074)
低速长航时无人机垂直突风过载分析
李建华,刘凯,李平坤,李锋
(中国航天空气动力技术研究院 彩虹无人机科技有限公司,北京 100074)
低速中空长航时无人机的升力非线性较强,利用标准离散突风模型和连续紊流模型计算得到的突风过载差别较大。针对该问题,本文采用改进的离散突风模型求解突风载荷,即直接求解突风条件下原始的运动学方程,并在运动历程中考虑非线性升力的影响。结果表明:改进的离散突风模型计算得到的突风载荷明显低于标准离散突风模型所得的载荷,更贴近无人机的实际情况,且改进的离散突风模型与连续紊流模型的计算结果也相近。
中空长航时;无人机;突风载荷;离散突风;连续湍流
0 引 言
基于长时间监视和打击任务需求,低速中空长航时无人机发展迅速。由于对长航时和载荷能力的需求,低速中空长航时无人机通常具有高升阻比、巡航速度低(巡航升力大)、翼载较小等技术特点。上述特点致使该类无人机在遭遇突风时会产生很大的突风过载,且低速中空长航时无人机一般不作急剧的机动飞行,相对于机动载荷,其最严重的载荷状态通常由突风载荷决定。因此,在多数情况下,突风载荷将作为结构设计或强度分析的依据,合理确定突风载荷对结构初始设计和确保飞行安全具有重要意义。
突风载荷包括离散突风和连续紊流载荷,对应的分析方法有离散突风模型和连续紊流功率谱模型。离散突风模型基于可能遭遇的最大过载思想[1],模型概念直观清晰、形式简单、所需参数较少;连续紊流模型基于功率谱概率设计思想,考虑各频率对载荷的影响,使用弹性模态并计及结构弹性效应,更适用于对弹性飞机及部件的过载分析。目前,虽然发达国家越来越重视对连续紊流突风的研究,但仍保留离散突风的要求,许多国家的适航标准和飞机公司要求须同时对离散突风和连续突风进行分析[2]。
低速长航时无人机通常采用大展弦比机翼,其升力线斜率大,翼载和飞行速度较低(相对于高速长航时飞机而言)。在相同的突风标准下,会造成突风载荷大(尤其是离散突风模型)。同时,离散突风模型和连续紊流模型的计算结果相差较大,在未开展真实飞行载荷谱测试的设计阶段,会给设计载荷系数的选取带来困难[3]。
标准的离散突风模型基于升力线性假设,而低速长航时无人机的升力存在较强的非线性。本文从突风条件下的运动学方程出发,通过直接求解原始的运动学方程,在运动历程中考虑实时非线性升力的影响,研究离散突风模型和连续紊流模型所得离散突风载荷的差别;分别采用国军标(或飞机适航标准)的离散突风计算方法和本文采用的改进的计算方法以及功率谱分析方法,对某低速长航时无人机离散突风和连续突风过载进行计算,给出该无人机初始阶段的设计过载。
1 离散突风模型
标准(国军标[4]和飞机适航标准[5])的离散突风模型一般选取“1-cos形”突风模型作为离散突风输入,将飞机简化为质点跟随突风的沉浮运动,采用突风减缓因子经验公式计算突风过载。标准规定的突风形状为
(1)
式中:Uds为某高度下的突风速度;s′为飞机进入突风区的距离;H为突风梯度,一般取为25倍平均气动弦长。
纵向垂直突风载荷系数的计算公式为
(2)
式中:Δn为由于突风引起的过载增量;Kg为突风缓和系数,其表达式为经验公式;ρ0为零高度空气密度;V为飞机当量空速;Cla为飞机升力线斜率;W为飞机质量;S为机翼参考面积;μg为质量参数;ρ为计算高度的空气密度;g为重力加速度。
标准的离散突风模型完全基于线性假设,升力线斜率作为常数处理,通常能够满足常规飞机的使用要求。为了获得高续航因子(巡航高升力和高升阻比),低速长航时无人机采用大弯度高升力翼型,这种翼型在距离巡航攻角不远处就易发生分离,造成升力强非线性,本文所用飞机的升力曲线如图1所示。同时,因无人机飞行速度较小,相对于常规飞机,在相同的突风强度下会造成更大的瞬时攻角,若按线性处理则会造成计算得到的突风过载偏大。研究发现,某些状态下采用标准离散突风模型得到的突风过载远大于“最大升力过载”,不符合物理规律。

图1 升力系数曲线
针对上述问题,本文从离散突风条件下原始的运动学方程出发,结合已知的无人机升力分布,采用实时攻角下真实的升力线斜率代替标准模型中的定值,但要利用实时升力线斜率,还需要得到实时攻角。要实现上述目的,可以从原始方程出发,通过数值方法求解整个运动历程,在运动历程中带入实时升力线斜率。下文将给出运动方程的推导过程,与之相似的推导过程可参见文献[2]和文献[6]。
突风状态下的运动学方程(减去平衡态)为
(3)
式(3)左边第二项表示由于沉浮运动带来的升力变化;右边表示突风带来的升力变化。
将式(3)进行微元处理,并考虑运动过程中的非定常效应和突风穿越过程,非定常气动力可用Wagner函数和Küssner函数表示,再利用卷积积分方法,则突风状态下的运动方程变为
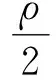
(4)
式中:Kw(t)和KG(t)分别为Wagner函数和Küssner函数。
引入突风模型,通过求解方程(求解方法详见文献[7])可以得到突风条件下不同时刻的位移和攻角,进而可得加速度和过载增量,不同时刻的突风过载为

(5)
2 连续紊流模型
功率谱模型使用频谱法把大气湍流环境描述为连续随机过程,目前大部分标准采用Vonkarman突风模型,大气紊流的功率频谱密度为

(6)
式中:φ为功率谱密度;σ为突风速度均方根值;Ω为折算频率;L为紊流尺度。

(7)
式中:Uσ为限制突风速度。
要得到准确的连续湍流响应函数和功率谱,需要进行包含刚体运动、弹性自由度、操纵和增稳系统的动力学分析[8-9]。在初始设计阶段,动力学分析过于复杂,所需的大量输入参数也很难给出。K.L.Peele[1]将飞机作为刚体考虑,给出了连续湍流突风响应的评估方法,所需参数也大幅减少,虽然在使用上具有一定限制,但在无人机初始设计阶段或对于飞机刚性较强的无人机仍然适用;且涉及的组合参数都被图表化,方便计算出无人机的连续突风载荷,具体公式及求解过程详见文献[1-2]。
3 突风过载计算分析
分别利用标准离散突风模型和离散突风改进算法以及功率谱模型计算某低速长航时无人机两种飞行状态的突风过载,所需的初始计算参数及结果如表1所示。
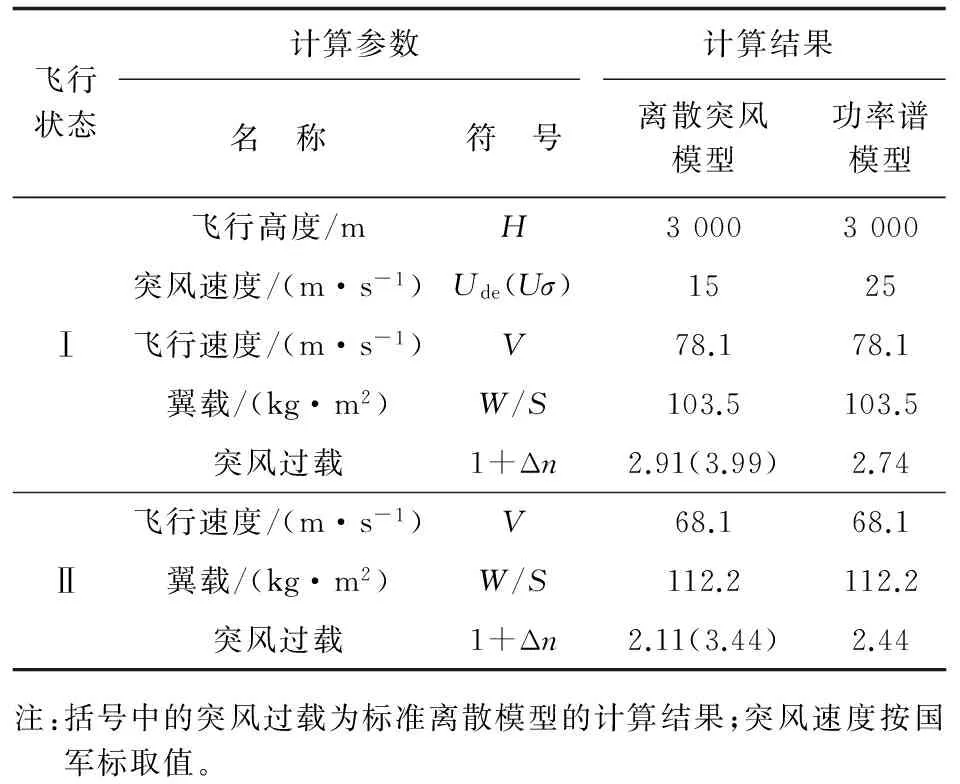
表1 突风载荷计算参数及结果
针对无人机两种不同的飞行状态,采用标准突风模型得到的最大突风过载分别为3.99(状态Ⅰ)和3.44(状态Ⅱ),而直接利用最大升力分析得到的“最大升力过载”分别为3.90(状态Ⅰ)和2.87(状态Ⅱ),可以看出,利用标准突风模型得到的过载值明显偏大,且不符合物理规律。其原因是,标准突风模型完全基于线形假设,采用固定的升力线斜率参数;而低速长航时无人机的升力存在较强的非线性,致使计算得到的突风载荷值偏离实际情况;改进的突风模型,由于考虑了突风运动过程的非线性影响,采用该模型计算所得的突风过载明显小于标准突风模型,两种状态的最大突风过载分别为2.91(状态Ⅰ)和2.11(状态Ⅱ)。
对比离散突风模型和连续湍流功率谱模型得到的突风过载,发现采用标准突风模型和功率谱模型得到的最大突风过载差别较大,载荷增量Δn相差71.8%;而采用改进的离散突风模型,其最大突风过载和连续紊流功率谱模型的最大过载接近,最大突风载荷增量偏差仅为9.8%。进一步分析可知,国军标离散突风模型完全基于线形假设和经验拟合曲线,对升力线线型、飞行速度和突风速度依赖性强;而连续紊流模型,考虑的参数更多一些,且考虑了不同频率的影响,标准的Von karman突风模型,其不同频率分别对应不同的突风速度,在大部分频率范围内其输出载荷功率谱能反映该频率下的实际载荷,故在低速长航时无人机上连续紊流模型得到的载荷谱更接近真实情况。而改进的离散突风模型,其回归到求解最原始的动力学方程,在运动历程中带入真实的攻角信息,相对于原始模型得到的载荷也更加贴近实际载荷。在未对飞机真实的载荷谱进行充分研究之前,一般要求同时对离散突风和连续突风进行分析,两种模型得出的最大突风过载相吻合,该结果利于无人机初始设计载荷的提出和初始结构方案的设计。
4 结束语
针对离散突风模型和连续紊流模型得到的突风过载差别较大,结合低速长航时无人机升力非线性较强的特点,本文从突风条件下原始的运动学方程出发,对离散突风模型的求解方法进行适当改进,改进后的方法计算得到的结果明显低于标准离散突风模型所得的载荷,更贴近无人机的实际情况,且离散突风与连续紊流模型计算结果相近。这对低速长航时无人机初始设计载荷的提出和结构方案设计具有重要意义。
[1] Peele K L. A method for estimating some longitudinal and lateral rigid-body responses of airplanes to continuous atmospheric turbulence[R]. NASA TND-6273, 1971.
[2] Frederic M H. Gust loads on aircraft: concepts and applications[M]. USA: AIAA Education Series, 1988.
[3] 詹光, 孙颖. 某高空长航时飞机垂直突风过载计算分析[J].飞机设计, 2007, 27(6): 7-9. Zhan Guang, Sun Ying. Computation of longitudinal gust load for a HALE vehicle[J]. Aircraft Design, 2007, 27(6): 7-9.(in Chinese)
[4] GJB67A-2008军用飞机强度和刚度规范[S]. 北京: 国防科学技术工业委员会, 2008. GJB67A-2008 Military airplane structural strength specification[S]. Beijing: COSTIND, 2008.(in Chinese)
[5] 中国民用航空局. CCAR-25-R4运输类飞机适航标准[S]. 北京: 中国民用航空局, 2011. Civil Aviation Administration of China. CCAR-25-R4 Airworthiness standards: transport category airplanes[S]. Beijing: CAAC, 2011.(in Chinese)
[6] Pratt K G, Walter G W. A revised gust-load formula and a re-evaluation of v-g data taken on civil transport airplanes from 1933 to 1950[R]. Technical Report Archive & Image Library NACA-TR-1206, 1953.
[7] Houbolt J C, Kordes E E. Structural response to discrete and continuous gusts of an airplane having wing bending flexibility and a correlation of calculated and flight results[R]. Technical Report Archive & Image Library NACA-TR-1181, 1954.
[8] 杨秋艳, 王育林. 飞机连续阵风载荷计算方法应用研究[J]. 飞行力学, 2008, 26(4): 65-68. Yang Qiuyan, Wang Yulin. Research and application of the continuous gust loads analysis method for aircraft[J]. Flight Dynamics, 2008, 26(4): 65-68.(in Chinese)
[9] 刘晓明, 万少杰, 熊峻江, 等. 民机飞行载荷谱编制方法[J]. 北京航空航天大学学报, 2013, 39(5): 621-625. Liu Xiaoming, Wan Shaojie, Xiong Junjiang, et al. New approach for generating flight load spectrum of civil aircraft[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(5): 621-625.(in Chinese)
(编辑:马文静)
Computation of Longitudinal Gust Load for a Low Speed Long Endurance UAV
Li Jianhua, Liu Kai, Li Pingkun, Li Feng
(Rainbow UAV Technology Co., Ltd., China Academy of Aerospace Aerodynamics, Beijing 100074, China)
There is a significant gust-loads difference between the normal discrete-gust model and continuous-turbulence model because of the strong lift nonlinearity of a low speed medium altitude long endurance(MALE) UAV. To solve this problem, an improved discrete-gust model is adopted, namely, the kinematic equation of gust load is solved and the nonlinear lift is also considered during the moving course. Result indicates that the gust load obtained by the improved method is smaller than that by normal discrete-gust model, and which is close to the actual gust load. At the same time, the gust load is accordance with that computed by continuous-turbulence model.
medium altitude long endurance(MALE); UAV; gust load; discrete-gust; continuous-turbulence
2017-01-11;
2017-03-07
李建华,ssanliren@126.com
1674-8190(2017)03-304-04
V211.3
A
10.16615/j.cnki.1674-8190.2017.03.009
李建华(1977-),男,硕士,高级工程师。主要研究方向:无人机总体、气动设计。
刘 凯(1979-),男,高级工程师。主要研究方向:无人机总体设计。
李平坤(1977-),男,硕士,研究员。主要研究方向:无人机飞行控制、总体设计。
李 锋(1961-),男,博士,研究员。主要研究方向:流体力学、无人机总体设计。

