双基前视SAR的Chirp Scaling成像算法

文/王波 佴俊

双基前视SAR的Chirp Scaling成像算法

文/王波 佴俊

双基协同前视可以突破单基SAR无法实现正前视成像的瓶颈。本文在基于级数反演理论推导获得任意构型双基SAR二维频谱精确表达式的基础上，提出了一种适用于平飞等速前视双基SAR的Chirp Scaling成像算法，该算法通过沿距离向补充多普勒补偿来提升距离徙动矫正精度，获得很好的聚焦效果。计算机仿真结果验证了本文算法的有效性。

双基地 合成孔径雷达 前视 级数反演 成像算法

1 引言

在现代高科技的局部战争中，空对地精确打击的地位日益重要，高分辨率前视成像是实现空对地精确打击亟待解决的关键技术之一。实波束能够前视成像，但过低的分辨率远不能满足精确制导的要求。单基SAR技术和DBS技术能够在正侧视和斜视模式下获得高分辨率图像，但无法实现平台飞行方向正前方的高分辨率成像。双基SAR系统依靠灵活的构型，使得接收平台正前方观测区域的等距离线和等多普勒线准正交，进而能够实现高分辨率前视图像，这在空对地精确打击和飞机着陆等方面均具有十分重要的应用前景。此外，相对于单基SAR而言，收发平台分置的双基SAR系统在平台安全性、抗干扰性能以及目标识别等方面具有显著的优势。

2 基于级数反演的二维频谱

为了更好的描述点目标的斜距历程，我们重新引入了相关参量，重新构建了任意构型双基SAR的空间几何关系，如图1所示。发收平台的直线运动，速度方向具有任意性，速率分别为VT和VR。在合成孔径中心时刻，发收平台到点目标的斜距分别为R0T和R0R，斜视角分别为θ0T和θ0R。

设合成孔径中心时刻为方位参考时刻，根据几何关系，该点目标斜距历程可以表示为

双基SAR回波信号经过距离向傅里叶变换后可表示为

其中fτ为距离向频率，TS为合波束对应的合成孔径时间，γ为线性调频信号的调频率，TP为发射信号脉冲宽度。通过方位向傅里叶变换可以得到点目标回波信号的二维频谱

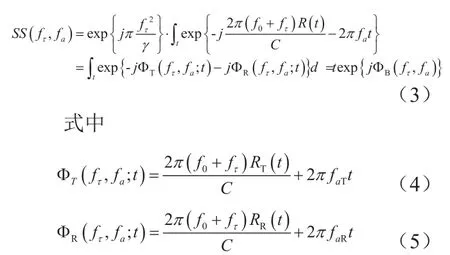
各类频域成像算法的精确程度在很大程度上决定于定目标回波信号二位频谱的精确程度。在双基SAR系统中，点目标的斜距为发收平台到点目标的斜距之和，斜距历程的表达式具有双根号形式，这就致使在方位相傅里叶变换的推导过程中，无法直接利用驻定相位原理来推导出点目标二维频谱的解析表达式。Neo提出的MSR方法[4]能够获得任意构型双基SAR的精确二维频谱，具有普适性

图1：任意构型双基SAR几何关系

图2：距离多普勒域中距离徙动示意图

图3：平飞前视双基SAR几何构型

3 平飞等速前视双基SAR的CS成像算法

在距离多普勒域中进行CS处理，完成差分距离徙动校正，CS操作的相位为

表1：平行前视双基SAR仿真参数

表2：前视双基SAR点目标质量评估

CS操作后，通过距离向傅里叶变换得到二维频域的信号，在二维频域乘以距离补偿因子完成距离聚焦处理和一致距离徙动校正。距离补偿因子可以表示为

上式中，第一项完成距离向聚焦和二次距离压缩，这里忽略了二次距离压缩项的距离空变。第二项完成一致距离徙动的校正，与单基SAR的CS算法相比，该项的形式有所不同，这是由于距离徙动以及CS因子表达式不同而决定的。

完成距离补偿后，对信号进行距离向逆傅里叶变换，然后在距离多普勒中乘以方位补偿因子完成方位向聚焦和残余相位补偿。方位补偿因子可表示为

其中，第一项完成方位向聚焦和方位向位置校正，第二项补偿CS操作引起的残留相位。第一项中的对应的具体表达式为

平飞前视双基SAR系统中，根据式，零时刻斜距为R0的点目标的距离徙动所对应的时延为

以参考点距离徙动所对应的时延作为参考时间，时延差为

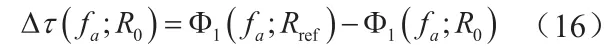
在参考多普勒频率处的时延差为

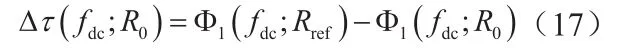
本文采用一种简单的数值计算方法来求解CS因子，该过程由以下几个步骤组成：

（1）在观测场景内选取一个参考矢量Q，沿该矢量方向均匀的布置若干个点目标，覆盖整个场景。

（2）计算每个点目标在零时刻所对应收发斜距以及斜视角，然后根据式（2）计算每个点目标斜距历程所对应的各项系数。

参考矢量Q的选择在理论上应该是任意的。根据梯度理论，有如下结论：参考矢量垂直于多普勒梯度矢量在地面的投影分量时，多普勒中心频率的变换最小。本文参考矢量的选择就是基于这一结论。

图5给出了CS处理前后，场景内点目标斜距的变化。横坐标为零时刻的斜距差，纵坐标为CS后点目标位置的变化量，单位为距离单元。该图能够说明两点问题：

（1）即使本文选择了最佳的参考矢量，但多普勒中心频率在场景内的变化仍然较大，使得点目标零时刻的斜距差与多普勒中心频率处对应的斜距差不相等，两者之间的差距超过了一个距离单元，因此CS因子的计算应该以参考多普勒频率处对应的斜距差作为拟合时候的自变量；

图4：平行等速前视双基SAR的CS算法流程

图5：CS处理前后斜距的变化

图6：距离徙动拟合误差

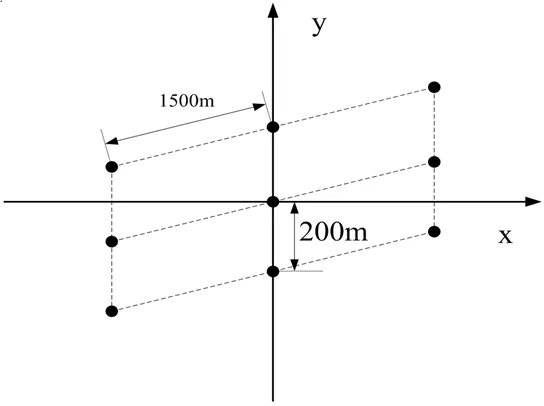
图7：双基前视SAR仿真场景

图8：双基前视SAR全场景成像结果

（2）通过CS操作进行补余距离徙动校正，点目标在距离向的位置由参考频率多普勒频率时刻所对应的斜距所决定，不再是该点目标在零时刻的斜距，当两者之间的差距超过一个距离单元时，在方位聚焦时应该对多普勒参数进行插值，然后逐距离门更新多普勒参数，提高方位向的聚焦精度。

本文在计算CS因子的时候采用的是线性拟合的方法。线性拟合后，在距离多普勒与中，残留的距离徙动量如图6所示。测绘带宽度为3km，最大的残留距离徙动量为0.35m左右，小于半个距离分辨单元，不会影响方位向的聚焦。

4 仿真实验

为了验证本文所提方法的有效性，我们进行一组前视双基SAR的仿真实验。仿真过程中，没有考虑天线方向图加权。仿真参数如表1所示。空间几何构型如所示。仿真是场景坐标系中布置的点阵如图7所示，图中的斜线代表参考矢量。在参考矢量上，两个点目标之间的距离为1500m。本次实验采用的仿真参数所对应的参考矢量的斜率接近于零，所以测绘带宽度接近3000m。竖线相连的三个点目标到收发平台的最短斜距和相等，满足方位平移不变性，成像后处于同一距离门。

点目标成像后的二维等高图、方位剖面图和距离剖面图如图9所示。第一行的各项指标与图8中左上角的点目标对应，第二行与中间的点目标对应，第三行与右下角的点目标项对应。由于前视SAR系统中，即使选择了合适的参考矢量，多普勒参数随距离的变化还是较为显著，导致最后的频谱扭曲严重，对点目标图像的质量评估带来困难，所以本文在仿真过程中，特意提高了距离向采样率，以适应频谱在距离向的扭曲。

左上、中间和右下三个点目标成像质量的评估结果表2所示。由于频谱扭曲严重以及插值方法和精度的限制，右下角点目标的距离向指标评估结果有些偏差，这一点也在其距离向剖面图上有所发应。

5 结论

本文提出了一种适用于前视双基SAR精确聚焦成像的CS算法。考虑到前视双基SAR系统多普勒参数随距离的剧烈变化这一特性，本文选择了一个最佳的参考矢量以减小多普勒中心频率的变化，提出了一种更为精确的CS因子计算方法，分析了沿距离向更新多普勒参数时插值的必要性。仿真结果表明，本文提出的CS算法能够实现前视双基SAR的精确聚焦成像。

图9：双基前视SAR点目标成像结果

[1]Cardillo G.P..On the Use of the Gradient to Determine Bistatic SAR Resolution.Proc.APS Int. Symp.,1990：1032-1035.

[2]Espeter T.,Walterscheid I.,Klare J. et al.Bistatic Forward-Looking SAR：Results of a Spaceborne-Airborne Experiment[J].IEEE Trans.Geosci. Remote Sens.,2011,8(04)：765-768.

[3]Walterscheid I.,Espeter T.,Klare J.,et al.Potential and Limitations of Forward-Looking Bistatic SAR[C]. Proc.IGARSS,2010：216-219.

[4]Neo Y.L.,Wong F.H.and Cumming I. G..A Two-Dimensional Spectrum for Bistatic SAR Processing Using Series Reversion [J].IEEE Geosci.Remote Sens.Lett.,2007,4(01)：93-97.

[5]Wong F.H.,Cumming I.G.and Neo Y. L.. Focusing Bistatic SAR Data Using the Nonlinear Chirp Scaling Algorithm [J].IEEE Trans.Geosci.Remote Sens.,2008,46(09)：2493-2505.

[6]Loffeld O.,Nies H.,Peters V.,et al. Models and Useful Relations for Bistatic SAR Processing [J].IEEE Trans.Geosci.Remote Sens.,2004, 42(10)：2031-2038.

[7]Wang R.,Loffeld O.,U1-Ann Q.,et al.A Bistatic Point Target Reference Spectrum for General Bistatic SAR Processing [J].IEEE Geosci.Remote Sens.Lett.,2008,5(03)：517-521.

[8]Wang R.Loffeld O.Neo Y.L.,et al. Extending Loffeld’s Bistatic Formula for the General Bistatic SAR Configuration[J].IET Radar Sonar Navig.,2010,4(01)：74-84.

[9]Liu B.C.,Wang T.and Bao Z..An Analytical Method of Updating the Range Derivatives and a Simple Image Registration Method for the MSRBased Range Doppler Algorithm [J]. IEEE Trans.Geosci.Remote Sens., 2010,7(04)：831-835.

[10]李燕平,邢孟道,井伟,等.一种双基SAR的SR-ECS成像算法[J].自然科学进展,2008,18(03)：323-333

[1 1]Z h o n g H.a n d L i u X..A n Effective Focusing Approach for Azimuth Invariant Bistatic S A R P r o c e s s i n g [J].S i g n a l Processing,2010,90(01)：395-404.

作者单位 南京电子技术研究所 江苏省南京市 210039

王波（1983-），男，湖北省武汉市人。工学硕士。工程师。主要研究方向为雷达系统技术。

佴俊（1979-），男，江苏省扬州市人。大学本科学历。工程师。主要研究方向为机载雷达总体技术和机载雷达售后服务综合管理。