持续攻击下的无标度网络修复策略研究

李一刚，王向东

（沈阳工业大学 信息科学与工程学院，辽宁 沈阳110870）

持续攻击下的无标度网络修复策略研究

李一刚，王向东

（沈阳工业大学 信息科学与工程学院，辽宁 沈阳110870）

针对随网络演化的持续性攻击，并且节点不可修复的情况，本文提出了一种加入限制参数的连边补偿修复方法。通过仿真实验验证了这种修复策略能够保证网络在演化过程中一直保持较好的连通性，能够保证网络中有百分之八十五以上的节点保持联通。并且在网络进行修复之后，不改变网络的无标度结构特性。

复杂网路；无标度网络；持续性攻击；攻击策略；修复策略

随着复杂网络的研究和发展，现今很多领域上的网络都可以看作是复杂网络。比如：internet网络[1]，电力系统网络[2]，交通网络[3]，军事网络[4]，自然网络[5]，社会关系网络[6]，生物网络[7]等。这些网络在各个领域中都起着十分重要的作用，因此对这些网络的研究十分必要。

在现实中的网络，大多为无标度网络。在无标度网络中，大多数的节点只有少量的连接度，而少数节点拥有大量的连接度。由于这种无标度网络的这种无标度特性，使得其对于随机的攻击有一定的抗毁性，但是对于蓄意有针对性的攻击十分脆弱[8]。一旦针对无标度网络发起了蓄意的攻击，将会对网络的连通性造成极大的损伤。因此对无标度网络在蓄意攻击下的修复策略研究十分必要。目前对复杂网络的修复研究，大多都是基于被攻击节点可修复的情况进行修复的[9-15]。这些研究将不同领域中的网络抽象为复杂网络，将修复人员及资源抽象为网络的修复因子，并且按照一定的策略分配，得出每个节点被修复的概率，从而按照这种概率对网络进行修复。其中的分配策略大致可分为平均分配策略和按照度进行重点分配的策略，并且得到了不同的修复效果。

需要注意的是，以上的修复策略都是在被攻击节点可修复的情况下修复的。然而在实际中，有很多被攻击节点不可被修复或者被攻击断掉的连边不可修复的情况。比如：攻击强度大，使得被攻击节点被摧毁；资源不冗余，无法调配多余的资源对故障节点进行修复；节点的修复需要较长的修复时间周期，针对故障节点修复无法立刻恢复网络连通性。在诸如此类的情况下，如果无法及时的恢复网络的连通性或功能，将会造成极大的影响和危害。所以，研究被攻击节点无法被修复的情况下的修复策略是有意义的。对网络的攻击除了一次性的攻击以外，还可能是持续的。这种持续可以是随着复杂网络演化同时进行的，长期的攻击。比如，对交通网络进行攻击，炸毁了其主要的交通线路，并在交通网络演化了一定时间后，再次攻击。这种攻击显然是持续的，并且被攻击的目标不容易被修复。针对这种攻击方式，本文研究了无标度网络，在随着网络演化课持续的攻击下，被攻击节点无法进行修复时的修复策略。除此之外，本文还研究了在本文的修复策略下，修复后的网络的无标度特性以判断修复后的网络是否还有攻击前网络的结构特点。

1 攻击模型

1.1 初始网络

文中的初始网络是由n个节点构成的无标度网络。该网络是不断演化的，每次演化网络中加入一个新节点。这个新节点根据网络中原有节点的度，择优建立m条连边。式（1）表示了这种择优策略：

其中，P（i）为第 i个节点被选中的概率；k（i）为网络中第i个节点的度；K为网络中所有节点度之和。

1.2 攻击策略

文中的攻击策略是持续性的，蓄意的攻击。被攻击的节点将断掉一部分边，并且这些连边无法被重新修复。对网络的攻击随着网络的演化同时进行，网络每演化一步，都根据概率r来判断是否进行攻击。每一次攻击会攻击x个节点，其中x是（0，X]中的随机整数。对于每一个被攻击的节点，会有一个攻击成功的概率r’。每一个被成功攻击的节点，都会断掉一部分边。本文中，这个被攻击断的边的比例设定在[0.5，1]，也就是说，被攻击的节点最少断掉其原有连边的一半，最多则断掉了其原有的所有连边。

1.3 修复策略

由于本文中的攻击是不可修复的，因此，因攻击而断掉的边没有重新连接的可能。针对这种情况，本文采用的是连边补偿的方法，即被攻击节点连接的相邻节点，与网络中的其他节点建立新的连边。本文中用网络中最大子网络的节点个数和整个网络所有节点个数的比值来表示最大连通子图在网络中所占的比例，从而用来评价网络的连通性。这里需要考虑的是，如果每一次修复，令被攻击节点的原所有相邻节点都建立新的连边，会造成过度修复，在实际中可能会造成资源的浪费或者由于资源不足根本无法实现。因此，本文中提出了两个体现网络结构特征的限制参数，来作为网络修复的标准。这两个参数分别为：

1） M=Max（k）/L；

2） LCG=lcg/L；

其中，Max（k）代表在攻击发生之前，网络中最大节点度，lcg表示当前状态下，网络中最大连通图所含有的节点个数。L表示网络中所有连边的数量。以这两个比值作为体现网络结构状态的标准，并按照不超过这个标准的强度进行修复。这两个参数分别代表了网络中最大度数和最大连通图节点个数与网络中连边数量之间的比值关系。因为本文中的修复策略是利用建立新的连边的方法进行补偿的，所以过度修复也就是说建立了过多条的新连接边。当M或LCG较小时，说明L相对较大，即网络中的连边偏多。因此在修复时，只有在现在的此时的M和LCG值大于标准值时，才进行修复，用这种方法来避免过度修复。并且本文通过仿真还发现，加了这两个参数的修复策略还可以使得修复后的网络与原网络有同样的无标度特性。

具体的修复步骤如下：

1）由10个全连通的初始节点，按照无标度网络的演化机制，生成初始的无标度·1网络，含有n个节点，并计算此时的M值。网络如果在不受到攻击的情况下，LCG会趋于一个定值，因为在不受攻击的情况下，根据无标度网络的择优演化机制，网络在节点数足够多时，会达到全连通的状态。设每次网络增加m条边，则当演化到节点数足够多时，因此，LCG会随着网络演化趋于一个定值。这里将所研究的网络中的这个定值记作LCG。将M和LCG作为之后网络修复的标准；

2）网络开始演化，每次演化增加一个新的节点，并根据网络中节点的度择优建立m条新的连边，设网络中第i个节点度为k（i），K为网络中所有节点度之和，则节点被选中建立新连边的概率为P（i）=k（i）/k；

3）在演化的同时，按照概率r来判断是否发生攻击。若发生攻击，则在（0，X]区间内选取随机整数x，并按照节点度由高到低选取x个节点进行攻击。对每个节点的攻击会按照概率r’来判断攻击是否成功。若攻击成功，被选中的节点会被攻击断掉一部分比例的边并且无法修复，这个比例本文中选取[0.5，1]之间的随机值；

4）当攻击发生时，立即进行修复。修复时，被攻击节点的相邻节点中，失去边的相邻节点依次进行修复。 比如，被攻击节点为 N（i），其相邻节点为 N（1），N（2），N（3）…，攻击后，N（1），N（2），N（3）与 N（i）的连边被切断，此时对 N（1），N（2），N（3）依次进行修复。每次修复前计算当前的M值记作M’，以及当前网络的LCG值，记作LCG’。当此时的网络同时满足M’＞M和LCG’＞LCG时，给被修复节点择优建立一条新的连边，择优策略同上文提到的已节点度高低作为标准的择优策略。该节点修复完成后，对下一个失去边的相邻节点进行同样的判断和修复过程，直至所有失去变得相邻节点都判断和修复完成；

5）网络每次演化都会判断是否进行攻击，以及攻击后是否进行修复，当网络演化为N个节点的网络时，演化结束。

1.4 网络结构特性研究

文中的无标度网络修复策略研究，在以提高网络连通性为目标的同时，还兼顾了网络的结构特征。无标度网络的度分布对于高度数服从幂律分布，即：p（k）=λk-α。 其中 λ 为比值系数，k 为节点的度，α 为幂律分布指数，p（k）为节点度为k的概率。可以看出，无标度网络的幂律分布中，α是网络结构特性的表征，现实网络中，不同的无标度网络因其现实意义不同，α值也不完全相同。本文的研究为保证该修复在提高网络连通性的同时还可以保证网络的结构特征还符合修复前的网络。因此研究了在这种修复策略下，α值是否与原网络α值相近。

2 仿真分析

文中以演化的无标度网络为研究对象，对网络进行与网络演化同时的持续性蓄意攻击，使用连边补偿的修复策略进行了仿真实验。

初始网络为n=100的无标度网络，每演化一次，加入一个新节点并择优建立两条新的连边，即m=2，因此LCG=1/m=0.5。发生攻击的概率为r=0.5，每次攻击节点的个数x为（0，5]的随机整数，对每个目标节点攻击的成功概率r’设为0.4。每一个被成功攻击的目标节点都会按照随机比例切断一些连边，这个比例是在[0.5，1]内随机选取。修复策略则与上文所述相同。用网络最大连通图即最大连通图的节点个数与网络中总节点个数的比值来描述修复的效果。图1为不加修复策略，网络演化受到攻击时的仿真结果图。

图1 无修复策略网络连通性仿真图

其中，横坐标为随着网络演化，网络的总节点的个数，纵坐标为最大连通图所含节点个数与总节点个数的比值。

图2为加入本文的修复策略之后，修复效果图。

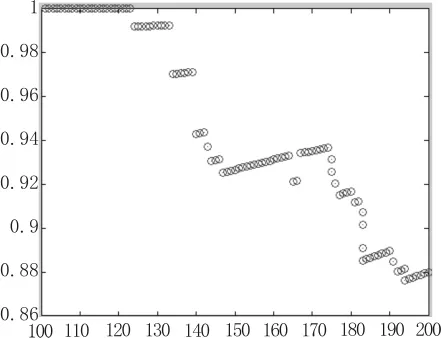
图2 有修复策略的网络修复效果图

可以看出，在不加修复的情况下，这种攻击会是网络的连通性受到较大的破坏，并且有较大的波动；但是在本文的修复策略下，网络的连通性得到了较大的提升，并且相对稳定。

无标度网络的度分布对于高度数的节点满足幂律分布，即 p（k）=λk-α。 现将其两边取对数，得：lnp=lnλ-αlnk。这表明，将p作为纵坐标，k作为横坐标，在双对数坐标系下，高度数节点的度分布曲线应该是近似一条直线的。其中-α为其斜率。因此，我们对网络在遭受的攻击前的度分布曲线和在遭受攻击并按照文中的修复策略进行修复后的度分布曲线进行了仿真分析，得出图3；对网络在遭对网络在遭受的攻击前的度分布曲线和在遭受攻击但是修复策略中没有引入两个限制参数（L和LCG）的度分布曲线进行仿真分析，得出图4。

图3 含限制参数的度分布曲线

图4 无限制参数的度分布曲线

其中，横坐标为k，纵坐标为p（k）。因为对于高度数的节点，这种幂律分布是近似的，所以在双对数坐标下的曲线也只能是近似直线。曲线1为在攻击发生前，原初始无标度网络的度分布曲线，图3中的曲线2为在网络随着演化承受攻击并按照本文的策略修复下的度分布曲线，图4中的曲线2为在网络随着演化承受攻击但是修复策略中没有引入限制参数（M和LCG）的度分布曲线。

图3中，若将量曲线高度数的部分近似看作直线，则两条曲线的斜率很接近，可以认为网络的结构特性没有改变；图4中，两条近似直线的斜率则相差很多，可以认为网络的结构特性发生了变化。可知，加入了两种限制参数，除了可以避免过修复，还可以保证修复后的网络与原网络具有几乎同样的无标度特性。

3 结 论

文中提出了在演化的蓄意攻击下，利用连边补偿并引入限制参数的修复策略通过仿真实验，可知该策略可以有效的提高网络的连通性并且不改变原网络的无标度特性。在不加修复的情况下，网络的连通性可被攻击最低达到0.4左右，并且最大连通图比值不稳定；在加入修复后，可使网络的连通性提升，使其最低也可达到0.85左右，并且可以保证整个过程网络连通的稳定性。另外在修复后，通过双对数坐标下的度分布曲线可看出，该加入了限制参数M和LCG的修复策略不改变网络的无标度结构特点。这表明这种修复策略不仅有理论意义，还有一定的实际价值。

[1]Gan C，Yang X，Liu W，et al.Propagation of computervirusboth acrossthe Internetand external computers:A complex-network approach[J]. Communications in Nonlinear Science&Numerical Simulation，2014，19（8）:2785-2792.

[2]TIAN Xu，JIE Chen，YUE He，etal，Complex network propertiesofchinese powergrid[J].International Journal of Modern Physics B，2012，18（17-19）:2599-2603.

[3]Hu MB，Ling X，Jiang R，et al.Dynamical hysteresis phenomena in complex network traffic[J].Physical Review E Statistical Nonlinear&Soft Matter Physics，2009，79（4 Pt 2）.

[4]XU Yu-Zhang，L Zhu，L Zhang.Information diffusion model of military communication network based on complex network theory[J].Journal of Military Communications Technology，2015.

[5]SM Shekatkar，G Ambika.Complex networks with scale-free nature and hierarchical modularity[J].European Physical Journal B，2015，88（9）:1-7.

[6]M Williams，J Burry，A Rao.Understanding social behaviors in the indoor environment:a complex network approach[J].Acadia Design Agency，2014:671-680.

[7]Yeh，Trai-Ming，Chuang，Yung-Chun.Multiobjective identification of controlling areas in neuronal Networks[J].IEEE/ACM Transactions on Computational Biology&Bioinformatics，2013，10（3）:708-720.

[8]刘涤尘，冀星沛，王波，等.基于复杂网络理论的电力通信网拓扑脆弱性分析及对策 [J].电网技术，2015，39（12）:3615-3621.

[9]胡斌，黎放.多种攻击策略下无标度网络修复策略[J].系统工程与电子技术，2010，32（1）:86-89.

[10]刘中华，胡兵，吴荣华.基于修复策略的舰艇编队复杂网络系统可靠性研究 [J].计算机科学，2012，39（6A）：139-141.

[11]狄鹏，黎放，胡斌.网络中心战模型修复策略研究[C]//Proceedings of International Conference on Broadcast Technology&Multimedia Communication，2010.

[12]王甲生，吴晓平，陈泽茂，等.修复策略下典型拓扑结构复杂网络抗毁性研究[J].海军工程大学学报，2015，27（4）：75-79.

[13]蒋勇，赵作鹏.多属性加权模糊贝叶斯的复杂网络故障自修复技术[J].计算机应用研究，2015，32（8）:2378-2381.

[14]王正武，周振宇，胡静.基于节点修复效果的故障路网修复策略[J].长沙理工大学学报：自然科学版，2014，11（4）:25-31.

[15]郑力明，李晓冬，罗建禄，等.复杂网络中修复策略研究[J].电子设计工程，2014，22（2）:140-142.

A repair strategy for scale-free network under the progressive intentional attack

LI Yi-gang，WANG Xiang-dong
（School of Information Science and Engineering，Shenyang University of Technology，Shenyang 110870，China）

To repair the scale-free network under the progressive and intentional attack which the attacked nodes and links couldn't be repaired，in this paper we propose a repair strategy base on the link compensation method with the limit parameters.We show this kind of repair strategy could keep the network has a stable connectivity.It could keep over 85%of the network nodes connected.Beyond that，this kind of repaired strategy won't change the scale-free structural characteristic of the primary network before attack and repair.

complex networks； scale-free networks； progressive attack； repair strategies

TN91

A

1674－6236（2017）17-0181-04

2016-07-16稿件编号：201607120

李一刚（1992—），男，朝鲜族，朝鲜人，硕士研究生。研究方向：复杂网络。