丰盈经历 理解算理
杨武昌


培养学生的计算能力是小学数学教学的核心任务之一。计算能力强弱的重要标志是对计算过程的深刻理解。理解计算过程不光要知道怎样计算,更重要的是要明确为什么要这样计算,这实质上是一个算理问题。“两位数乘两位数(不进位)笔算乘法”这一内容安排在人教版三年级数学下册第四单元。这部分知识是在学生已经掌握了“乘数是一位数笔算乘法”及“用整十数乘”的基础上进行教学的,它是学生进一步学习乘数是三位数乘法的基础。“乘数是一位数笔算乘法”的算理和算法都将直接迁移到两位数乘两位数中来。因此,学生对算理和算法的理解和探索并不会感到困难。本节课除了让学生理解两位数乘两位数笔算乘法的算理、掌握其算法以外,还承担着计算与应用两个任务。那么,在本课教学中,如何使计算教学与数学应用和谐交融,有机结合呢?
一、情境创设,支撑理解
小学数学课程标准强调,计算应使学生经历从现实生活中抽象数和简单的数量关系,在具体的情境中理解,并应用所学的知识解决问题的过程,避免将运算与应用割裂开来。教学中,教师要根据学生认知发展水平和已有的知识经验,选择学生感兴趣的事物、活动,用蕴含数学信息的故事、游戏、图片,创设各种生动形象的、与教材内容有关的教学情境,拓宽学生数学学习的视野,以激发学生学习兴趣,引导他们积极主动地参与到学习中去。
如,“两位数乘两位数(不进位)笔算乘法”的教学伊始,充分利用课本资源,借助多媒体课件创设这样一个学生熟知的情境:妈妈带小红去书店买课外书,每本14元,一共买了12本。一共要付多少钱?从而引导学生得出14×12的数学算式。通过这样创设简单、有效的情境不仅让学生从具体的生活问题中自然引出数的计算,改变枯燥的呈现方式,而且丰富了学生的学习过程,从而使学生感受到数学在实际生活中的应用价值。然而,计算教学的情境不是随便乱用,只有创设相当合适的教学情境,才会起到相得益彰的作用。如果创设的教学情境与学生的生活实际太远,或者情境的数学价值不大,学生便有可能毫无目的地发散出去。
二、数形结合,促进理解
在小学数学教学中,教师要从形对于数的直观性、数对于形的深刻性这两方面,发挥数形结合的作用。由此,数形结合既是研究、探索数学的一种思想方法,又是帮助学生理解、解释数学的一种教学方式与教学手段。在“两位数乘两位数(不进位)笔算乘法”的教学中可以借助数形结合,降低学生学习难度,帮助学生更好理解知识,架起算理与算法之间的桥梁,使抽象思维和形象思维有效地结合起来,从而帮助学生深刻地理解算理。
如,在“两位数乘两位数(不进位)笔算乘法”的教学中可结合上述情境创设的基础上,充分利用“点子图”帮助学生理解笔算过程中每一步的意义,使算理和算法达到有机融合。
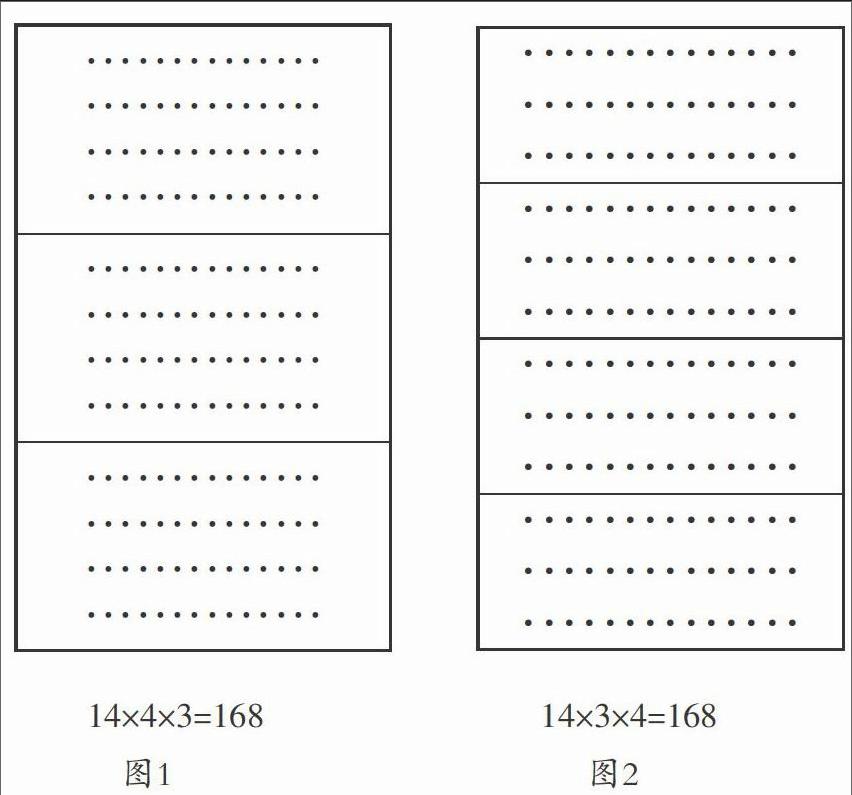
1. 把上下分成三个部分,每个部分都是14×4,再把三个部分相加得168(如图1)。
2. 把上下分成四个部分,每个部分都是14×3,再把四个部分相加得168(如图2)。
3. 把左右分成三个部分,前两部分都是12×5,第三部分是12×4,再把它们相加得168(如图3)。
4. 把上下分成两个部分,上部分是14×2,下部分是14×10,两个部分相加得168。(如下图4)。
……
当然,在交流14×12计算问题时,由于学生的认知建构和解决问题的视角不同,常常会出现不同的算法,教师要尊重学生的个性化算法,鼓励学生对同一个计算问题进行不同的算法思考,通过交流,体验算法的多样化。教师要善于引导学生通过对不同计算方法和点子图的分析比较、归纳和分类,多中选优、择优而用,掌握解题的策略。与此同时,教师可提出如下问题:“你的方法与他的方法不同在哪里?”“你认为他的方法怎么样?”“谁的方法更好些?”“用他的方法去做一做,你有什么想法?”提倡在算法多樣化的基础上关注算法的优化。上述教学中,通过运用点子图将学生的思考从直观的分一分、算一算,引导学生有意识地思考。这样既尊重算法的多样,呵护个性算法,又在尊重算法多样的前提下帮助学生完成对多样算法的优化,构建共性算法——“先分后合”,进而达到对算理的深层理解和对算法的切实把握。
三、理法通融,强化理解
《义务教育数学课程标准(2011年版)》指出:“学生获得知识,必须建立在自己思考的基础上,学生应用知识形成技能,离不开自己的实践;学生只有在获得知识技能的活动过程中,才能在数学思考、问题解决和情感态度方面得到发展。”理解“两位数乘两位数(不进位)笔算乘法”是本课的重点和难点。众所周知,算理是运算正确的前提和依据。算理和算法是计算教学中不可分割的两个方面,算理解决“为什么这样算”的问题,算法是算理的具体化,解决“怎样算”的问题。因此,计算教学中,教师要着力引导学生运用已有的知识技能去体验,让他们在具体的思考和探究中理解算理、掌握算法,从而实现算理与算法的有机融合,促进计算能力的不断提高。
如,教学“两位数乘两位数(不进位)笔算乘法”例1时,首先,引导学生结合点子图,让学生自主探究“14×12”怎样算?学生出现多种方法:(1)先算4套要多少钱,再算12套要多少钱;(2)先算3套要多少钱,再算12套要多少钱;(3)先算10套和2套各多少钱,再合起来;(4)用竖式计算。交流时,重点引导学生对(3)的理解,让学生有意识地先说2套是14×2=28,再交流10套是14×10=140,最后合起来是28+140=168。接着引导学生交流用竖式计算,努力架设算理直观与算法抽象之间的桥梁,可先引导学生思考第一层算的是什么?表示什么?第二层呢?表示什么?接下来的呢?(逐步板书如下:)
14
×12
28 ……14×2=28→2个14是28(2套的钱)
140 ……14×10=140→10个14是140(10套的钱)
168 ……28+140=168→12套的钱
然后,引导学生小结:刚才先算什么?第一个乘数与第二个乘数个位上的数相乘,算出了2套的钱。再算什么?与第二个乘数十位上的数相乘,算出了10套的钱,最后相加,算出12套的钱。
接着再让学生计算13×52,24×23。并引导学生观察,这些算式有什么共同的地方?通过观察比较,发现并规范竖式计算的简便写法。
最后,再引导学生交流:为什么新的算法第二个积的末尾要与十位对齐?为什么新的算法要把两次乘得的积分上下两层来写?
由此看出,教学中为学生架设了三座桥梁。第一,通过有意识交流第(3)种解法,为笔算算法的算理做好铺垫;第二,通过问题“算的是什么,表示什么”,引导学生把视角投向竖式计算的实际情境中,数形对应,使学生直观地理解算理,并在直观算理的支撑下,逐步抽象出算法。第三,安排学生尝试计算,并引导学生观察、比较“这些算式有什么共同的地方?”进而简化竖式。这样,学生充分体验了从算理到算法的演变过程,学生学得轻松、理解得更加深刻。
纵观这一内容的教学,对于学生而言,理解算理、建构算法往往是一个艰难的过程。因此,教师在引导学生理解算理和算法时,要注意沟通具体直观和抽象概括之间的联系;在引导学生感悟算理和算法时,要提供充分的时间和空间,让学生丰富体验、加深认识;在链接算理与算法时,要尊重学生的理解和选择,因势利导,有针对性地引导学生进行分析比较、反思交流等。只有这样,才能真正使学生达到算理、算法和技能的有机融合,学生也才能知算理、晓算法;以算理、释算法;依算理、用算法。从而提升学生的数学思维,同时为学生以后学习“两位数乘两位数(进位)笔算乘法”“三位数乘两位数笔算乘法”等提供有益的思维支持。

