二元fcc无序合金的晶格常数和体弹模量的第一性原理计算方法探究

刘继琼 鲁晓刚,2

(1.上海大学材料科学与工程学院，上海 200444；2.上海大学材料基因组工程研究院，上海 200444)

二元fcc无序合金的晶格常数和体弹模量的第一性原理计算方法探究

刘继琼1鲁晓刚1,2

(1.上海大学材料科学与工程学院，上海 200444；2.上海大学材料基因组工程研究院，上海 200444)

通过建立特殊准随机结构(SQS)，采用第一性原理VASP程序，用两种不同的弛豫方法分别对二元fcc Ni- X (X=Al,Au,Cu,Ga,Mo,Pt,Ta,W)无序合金的晶格常数和体弹模量随成分的变化进行了计算。这两种弛豫方法分别是离子弛豫法和体积弛豫法。最终计算结果表明，两种计算方法所得的晶格常数和体弹模量非常相近。因此在计算二元无序合金的晶格常数和体弹模量时，可以只做体积弛豫。这不仅大大简化了计算步骤，而且能够保持点阵的对称性，为计算二元合金的体积和体弹模量提供了准确高效的计算方法。

第一性原理 晶格常数 体弹模量 VASP SQS 离子弛豫 体积弛豫

晶格常数和体弹模量是材料的基本物理性质，对了解材料基本性质，进行热力学动力学计算[1]，及研究材料相变[2]有十分重要的意义，必须准确确定其随成分的变化规律。基于密度泛函理论[3]的第一性原理计算被广泛应用于材料的物理性质计算中，通常第一性原理方法多用于计算有序晶体的物理性质。而实际上，很多固溶体并不具有严格的有序结构。因此，1990年Zunger[4- 6]等提出了特殊准随机结构(SQS)的计算方法，即通过构建一个有序结构超胞(一般包括8～32个原子)，模拟A1-xBx的随机无序结构。本文采用16个原子的SQS[7]结构，对fcc Ni- X(X=Al, Au, Cu, Ga, Mo, Pt, Ta, W)合金在不同成分固溶时的晶格常数和体弹模量分两种弛豫方法进行计算，探究了不同弛豫方法对计算结果的影响。

1 计算方法简介

本文采用基于投影缀加平面波(PAW)[8]赝势的第一性原理计算方法，计算主要通过Vienna的第一性原理计算软件包—VASP[9]完成。采用交换关联广义梯度近似(GGA)[10]由Perdew、Burke及Ernzerhof(PBE)[11]进行参数化。布里渊区采用Monkhorst- Pack的K点网格(15×15×15)[12]，截断动能为400 eV。

本文选取16个原子的SQS模型。通过SQS建立5种晶胞结构，分别模拟无序合金AxB1-x5个不同的成分点：x=0.062 5, 0.25, 0.50, 0.75, 0.937 5。对于每一个成分采用两种弛豫方法进行计算。

第一种方法为离子弛豫法。计算分两步：第一步做离子弛豫，体积随晶格常数的改变而改变，采用Methfessel- Paxton smearing 方法；第二步计算利用第一步计算的波函数做静态计算，采用Blöchl修正的正四面体方法。第二种方法为体积弛豫法，即直接对一系列晶格常数点做静态计算。

每一个成分点的两种计算方法所得的不同的晶格常数和其对应的能量再通过MATLAB做Spline拟合，得到晶格常数- 能量曲线，曲线最低点即为该成分的平衡晶格常数，曲线二阶偏导即为该成分固溶体稳定存在时的体弹模量。

2 计算结果与讨论

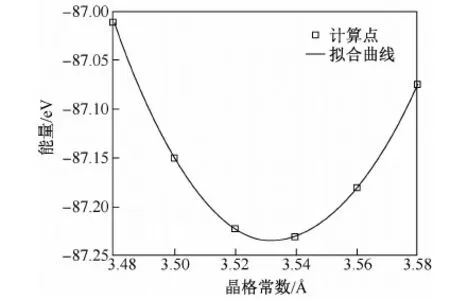
图1 fcc Ni- Al合金在Ni摩尔分数为0.937 5时，离子弛豫计算方法及MATLAB拟合得到的晶格常数- 能量曲线

图2 fcc Ni- Al合金在Ni的摩尔分数为0.937 5时，体积弛豫计算方法及MATLAB拟合得到的晶格常数- 能量曲线

下面以fcc Ni- Al合金在Ni的摩尔分数为0.937 5时为例。图1和图2分别为两种不同的弛豫方法计算拟合后得到的晶格常数- 能量曲线。

表1为MATLAB拟合得到的各成分下的晶格常数和体弹模量。由于没有计算点处的成分数据，故表1均只列出第一性原理计算值，只在图3中标出部分可测量点作为计算值佐证。图中a3为fcc Ni- Al合金的部分晶格常数试验数据。

图3 fcc Ni-Al合金两种计算方法所得晶格常数和体弹模量的比较(a3为试验值[13])

表2～表8是fcc Ni- X(Au, Cu, Ga, Mo, Pt, Ta, W)合金的晶格常数和体弹模量的比较结果。

表1 fcc Ni- Al合金两种弛豫计算方法的结果比较

表2 fcc Ni- Au合金两种弛豫计算方法的结果比较

表3 fcc Ni- Cu合金两种弛豫计算方法的结果比较

表4 fcc Ni- Ga合金两种弛豫计算方法的结果比较

表5 fcc Ni- Mo合金两种弛豫计算方法的结果比较

表6 fcc Ni- Pt合金两种弛豫计算方法的结果比较

表7 fcc Ni- Ta合金两种弛豫计算方法的结果比较

表8 fcc Ni- W合金两种弛豫计算方法的结果比较

从图3、表1～表8中可以看出，两种计算方法所得的晶格常数和体弹模量非常相近，因此对于计算二元无序合金的晶格常数和体弹模量时，可以只做体积弛豫。

3 结论

在计算二元无序合金的晶格常数和体弹模量时，只需对其体积做弛豫，即每一个不同的晶格常数点做静态计算即可。这不仅大大简化了计算步骤，而且能够保持点阵的对称性，为计算二元合金的体积和体弹模量提供了准确高效的计算方法。

致谢:

感谢上海市科委“重大工程用关键材料的集成计算材料工程开发”(项目号：14521100603)的支持。

[1] 吴春峰, 李慧改, 郑少波, 等. 二元合金热力学模型——Miedema模型[J]. 上海金属, 2011，33 (4): 1- 5.

[2] 徐祖耀. 纳米材料的相变[J]. 上海金属, 2002, 24(1): 11- 20.

[3] KOHN W, SHAM L J.Self- consistent equations including exchange and correlation effects[J].Physical Review, 1965, 140(4): A1133- A1138.

[4] ZUNGER A, WEI S H, FERREIRA L G, et al. Special quasirandom structures[J]. Physical Review Letters, 1990, 65(3): 353.

[5] WEI S H, FERREIRA L G, BERNARD J E, et al. Electronic properties of random alloys: Special quasirandom structures[J]. Physical Review B, 1990, 42(15): 9622- 9649.

[6] HASS K C, DAVIS L C, ZUNGER A. Electronic structure of random Al 0.5 Ga 0.5 As alloys: Test of the “special- quasirandom- structures” description[J]. Physical Review B, 1990, 42(6): 3757- 3760.

[7] WOLVERTON C. Crystal structure and stability of complex precipitate phases in Al- Cu- Mg- (Si) and Al- Zn- Mg alloys[J]. Acta Materialia, 2001, 49(16): 3129- 3142.

[8] BLÖCHL P E. Projector augmented- wave method[J]. Physical Review B, 1994, 50(24): 17953- 17979.

[9] KRESSE G, FURTHMüLLER J. Efficient iterative schemes for ab initio total- energy calculations using a plane- wave basis set[J]. Physical Review B, 1996, 54(16): 11169- 11186.

[10] PERDEW J P, CHEVARY J A, VOSKO S H, et al. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation[J]. Physical Review B, 1992, 46(11): 6671- 6687.

[11] PERDEW J P, BURKE K, ERNIERHOF M, et al. Generalized gradient approximation made simple[J]. Physical Review Letters,1996,77(18):3865- 3868.

[12] MONKHORST H J, PACK J D. Special points for Brillouin- zone integrations[J]. Physical Review B, 1976, 13(12): 5188- 5192.

[13] ELLNER M, KOLATSCHEK K, PREDEL B. On the partial atomic volume and the partial molar enthalpy of aluminium in some phases with Cu and C113 Au structures[J]. Journal of the Less- Common Metals, 1991,170(1):171- 184.

收修改稿日期：2016- 03- 08

Lattice Constant and Bulk Modulus of Binary Fcc Disordered Alloys Studied by the First- Principles Calculations

Liu Jiqiong1Lu Xiaogang1,2

(1. School of Materials Science and Engineering, Shanghai University, Shanghai 200444, China;2. Materials Genome Institute, Shanghai University, Shanghai 200444, China)

By establishing the Special Quasirandom Structures(SQS), the lattice constant and bulk modulus of fcc Ni- X (X=Al,Au,Cu,Ga,Mo,Pt,Ta,W) disordered alloy were calculated using the first- principles calculation program- VASP. Two kinds of different relaxation methods were used: ion relaxation method and volume relaxation method. By comparing the final computation results, it was found that the lattice constant and bulk modulus calculated by the two methods were very close. The volume relaxation scheme kept the lattice symmetry and provided a simpler and efficient way to calculate the volume and bulk modulus of binary alloys.

first- principles calculations, lattice constant, bulk modulus, VASP, SQS, ion relaxation, volume relaxation

上海市科委“重大工程用关键材料的集成计算材料工程开发”(No.14521100603)

刘继琼，女，主要研究方向为第一性原理计算与摩尔体积优化，Email：1242514900@qq.com

鲁晓刚，男，教授，主要研究方向为计算热力学、相变动力学模拟、多尺度集成计算、金属材料设计，Email：xglu@shu.edu.cn