基于模糊支持向量机的非平衡数据分类
陈辉辉,白治江
(上海海事大学 信息工程学院,上海 201306)
基于模糊支持向量机的非平衡数据分类
陈辉辉,白治江
(上海海事大学 信息工程学院,上海 201306)
支持向量机(SVM)作为一种有效的机器学习技术可以很好地处理平衡数据集,然而除了对噪声点和野点敏感以外,SVM在非平衡数据分类时会偏向多数类(负类)样本,从而导致少数类(正类)的分类精度变差。为了克服以上问题,提出了一种改进的模糊支持向量机(FSVM)算法。新算法在设计模糊隶属度时,不仅考虑样本到其所在类中心的距离,还考虑了样本的紧密度特征。实验结果表明,相对于标准SVM及已有的FSVM模型,新方法对于非平衡且含有噪声的数据集有更好的分类效果。
非平衡数据集;模糊支持向量机;模糊隶属度;样本紧密度
0 引言
支持向量机(SVM)是建立在统计学习中的VC维理论和结构风险最小化原则基础上的一种机器学习方法,因其在解决局部极小、维数灾难以及实现全局最优等问题上具有较好的泛化能力,已被普遍应用于各种样本集的分类问题中[1-2]。然而,标准的SVM不仅对噪声点或野点敏感,而且在处理非平衡数据集时,其决策面往往会向少数类(正类)偏移,从而导致对少数类(正类)的识别精确率降低。
目前,用SVM对非平衡数据集分类问题的研究主要集中在算法和数据两个层面。在算法层面,主要是对SVM训练模型进行改进以提高少数类的分类精度。VEROPOULOS K[3]提出了一种Biased支持向量机(BSVM)算法,在对样本的训练过程中赋予少数类(正类)较大的惩罚参数来保证少数类(正类)样本尽可能被分对,从而提高少数类(正类)的分类精度。FREUND Y和SCHAPIRE R E[4]在Boosting算法的基础上提出了一种改进的Adaboost算法,该算法在前一次分类结果的基础之上更新样本的权值,减少已被正确分类的权值,同时增加错分样本的权值,从而提高对不平衡数据集的分类性能。在数据层面,主要利用过采样技术和欠采样技术对数据集进行重采样。过采样主要包括随机过采样、SMOTE[5]算法等。文献[6]在SMOTE算法的基础之上,提出了一种基于混合重采样的SMOTE算法——HB_SMOTE算法。过采样方法虽然能够提高分类精确率,但是有可能增加算法复杂度。欠采样方法主要有随机欠采样、聚类欠采样等。采用欠采样虽然可以降低算法复杂度,但在删除样本时会造成样本信息缺失从而影响分类的精确性。
1 支持向量机简介
给定训练集(X,Y)={(xi,yi),i=1,2,…,n},其中xi表示样本,yi表示样本xi的标签,yi∈{1,-1}。针对非线性可分的数据,引入了非线性映射Φ:xi→Φ(xi),将训练样本xi映入高维空间。选取适当的核函数k(xi,yj)=Φ(xi)·Φ(xj)。引入松弛变量ξi≥0,i=1,2,…,n以及惩罚因子C。标准支持向量机(SVM)以如下形式表示:
s.t.yi(ωTΦ(xi)+b)≥1-ξi,ξi≥0,i=1,2,…,n
(1)
求解优化问题(1)的对偶问题:

(2)
假设对偶问题(2)最优解为α*,则最优超平面的法向量为:
(3)

(4)
由此可以得到决策函数为:
(5)
2 模糊隶属度的设计
在模糊支持向量机中模糊隶属度有着至关重要的作用,因为它决定了样本点对超平面的贡献度。目前,有很多方法来设计模糊隶属度函数,但是至今为止也没有一个统一的标准。文献[11]采用了根据距离来设计模糊隶属度的方法,把样本到其所属类的中心距离作为依据。文献[12]采用了S型模糊隶属度函数,把样本到其所属类的中心距离看做是一种非线性的关系。Lin Chunfu等人[6-7]学者提出了一个依据类中心来设计模糊隶属度的方案,使样本点对分类的影响随着样本点到其类中心距离的增大而减小,从而来降低噪声点或野点的影响。在文献[13]中模糊隶属度被定义为:
(6)

但是,这些设计方法都仅仅是将样本到其所在类中心的距离作为设计模糊隶属度的主要依据,对处于类中心的样本点赋予较大值的模糊隶属度,但是对于不平衡的数据集,这些设计仍存在把噪声样本作为正常样本来处理的可能性,从而导致分类结果的精确度降低。文献[14-15]提出了一种根据样本紧密度特征来设计模糊隶属度的方法,采用基于K近邻原则来设计样本紧密度,对于每一个训练样本xi,找到距离其最邻近的K个点,对于一个正类样本定义其样本的紧密度为:

(7)
同理,针对一个负类样本xi,它的紧密度可以定义为:
(8)
本文给出了一种设计模糊隶属度的新方案,在设计模糊隶属度时,不仅考虑样本到其所在类中心的距离,还考虑了样本的紧密度特征。结合样本到类中心的距离(公式(6))以及样本的紧密度(公式(7)、(8))来设计模糊隶属度,本文定义模糊隶属度如下:
(9)
其中,α∈[0,1],在本文中k的取值设为5。
3 惩罚因子的设计
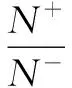
4 基于非平衡数据分类的模糊支持向量机算法
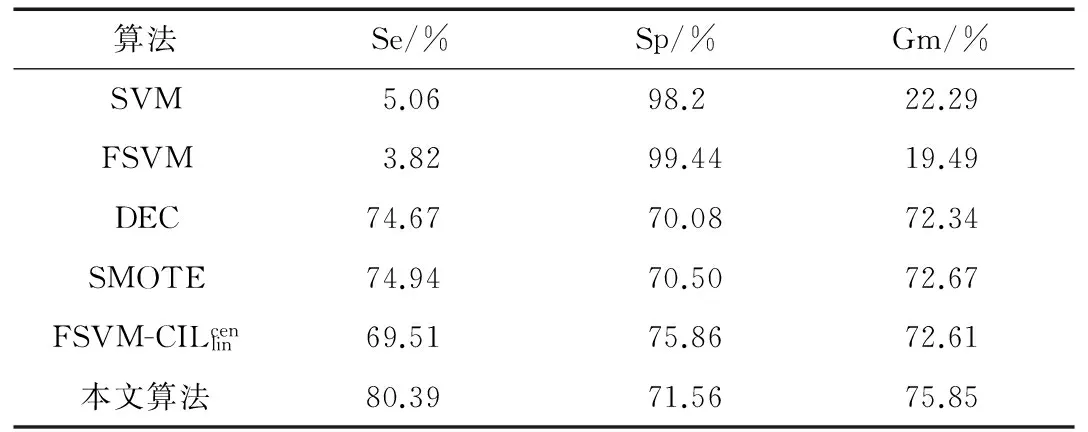
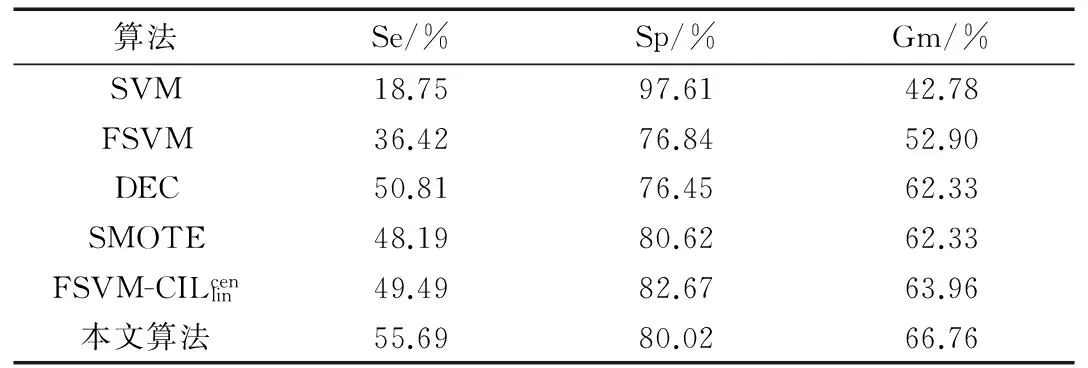
模糊支持向量机是在支持向量机的基础之上,依据样本在分类过程中的作用不同,为不同的样本赋予不同的模糊隶属度,以此来增大算法对噪声点或者野点的消除作用,提升分类结果的精确度。对于二分类问题,给定的训练集(X,Y)就转化成为模糊训练样本集(X,Y,S)={(xi,yi,si),i=1,2,3,…,n},其中xi是训练样本集,yi∈{1,-1}是样本标签,si(0 s.t.yi(ωTΦ(xi)+b)≥1-ξi,ξi≥0,i=1,2,…,n (10) 于是问题(10)的对偶问题如下: (11) 5.1 评价指标 表1 混淆矩阵 矩阵[13]如表1所示。 表1中的TP、FN、FP和TN分别表示分类正确的正类样本、不正确的负类样本、不正确的正类样本和正确的负类样本的数目,其中TP+FN=N+,FP+TN=N-。 然而,对于非平衡数据集的分类而言,已经不适合使用分类正确率来对实验结果评定,而是采用非平衡数据分类中的敏感性Se、特异性Sp和几何平均值Gm来进行评价,它们的定义如下: 其中,Se代表分类器预测正类样本的能力,Sp代表分类器预测负类样本的能力,Se和Sp的值越大表示分类效果越好。Gm表示分类器在非平衡数据集上的性能。 5.2 实验及结果分析 为了验证所提算法的合理性和有效性,从UCI机器学习数据库选择了5种不平衡的数据集来进行实验。由于数据集可能有几种类别,对于类别不是两类的就先把数据集都变为两类,选择其中某类当作正类,剩下的所有类合并作为负类。对Abanole数据集选择类标为15的当作正类,对Yeast数据集选择类标为5的当作正类,对Ecoli数据集选择类标为2的作为正类,对Haberman数据集选择类标为2的当作正类,对PimaIndians数据集选择类标为1的当作正类。这5种数据集的详细描述详如表2所示。 表2 数据集描述 表3 Abanole数据集在不同算法下的分类情况 表4 Yeast数据集在不同算法下的分类情况 表5 Ecoli数据集在不同算法下的分类情况 表6 Haberman数据集在不同算法的分类情况 表7 PimaIndians数据集在不同算法下的分类情况 针对不平衡数据集的分类,本文提出了一种改良的模糊支持向量机算法,在设计模糊隶属度时,不仅考虑样本到其所在类中心的距离,还考虑了样本的紧密度特征,以此来降低噪声点对分类结果的影响,同时结合DEC算法,从而更好地解决不平衡数据集的分类问题。最后,通过对5种不同数据集进行实验,验证了该算法的有效性。但是该算法在提高不平衡数据集分类精度的同时,也在一定程度上增加了算法的复杂度,如何在提高分类精度的同时降低算法的复杂度将是下一步研究的重点。 [1] CORTES C,VAPNIK V.Support-vector networks[J].MachineLearning,1995,20(3):273-297. [2] 程然.最小二乘支持向量机的研究和应用[D].哈尔滨:哈尔滨工业大学,2013. [3] VEROPOULOS K,CAMPBELL C,CRISTIMANINI N.Controlling the sensitivity of support vcetor machines[C].Proceedings of the International Joint Conferences on Artificial Intelligence,1999,4:55-60. [4] FREUND Y,SHAPIRE R E. A decision theoretic generalization of on line learning and an application to boosting[J].Jounal of Computer and System Sciences, 1997,119-139. [5] 郑文昌,陈淑燕,王宣强.面向不平衡数据集的SMOTE-SVM交通事件检测算法[J].武汉理工大学学报,2012,34(11):58-62. [6] 郭亚伟.基于混合重采样的非平衡数据SVM训练方法[J].微型机与应用,2016,35(12):52-54. [7] Lin Chunfu,Wang Shengde.Fuzzy support vector machines[J]. IEEE Transactions on Neural Networks,2002,13 (2):464-471. [8] 赵克楠,李雷,邓楠.一种构造模糊隶属度的新方法[J].计算机技术与发展,2012,22(8):75-77. [9] Qin Chuandong,Liu Sanyang,Zhang Shifang.Balanced fuzzy support vector machines based on imbalanced data sets[J].Computer Science, 2012,39(6):188-212. [10] BATUWITA R,PALADE V. FSVM-CIL:fuzzy support vector machines for class imbalance learing[J].IEEE Transactions on Fuzzy Systems,2010,18(3):558-571. [11] 练秋生,张伟.基于图像块分类稀疏表示的超分辨率重构算法[J].电子学报,2012,40(5):920-925. [12] 边肇祺,张学工.模式识别(第2版)[M].北京:清华大学出版社,2000. [13] 秦传东,刘三阳,张市芳.基于不平衡数据分类的一种平衡模糊支持向量机[J].计算机科学,2012,39(6):188-190. [14] 周广千,徐蔚鸿,杨志勇.一种新的模糊支持向量机算法[J].微计算机信息,2010,26(3):217-218. [15] 唐浩,廖与禾,孙峰,等.具有模糊隶属度的模糊支持向量机算法[J].西安交通大学学报,2009,43(7):40-43. [16] VEROPOULOS K,CAMPBELL C,CRISTIANINI N. Controlling the sensitivity of support vector machines[C]. International Joint Couference on Ai,1999:55-60. Imbalanced data classification based on FSVM Chen Huihui, Bai Zhijiang (Information Engineering College, Shanghai Maritime University, Shanghai 201306, China) As an effective machine learning technology, support vector machine (SVM) can effectively handle the balanced datasets. However, aside from being sensitive to the noise points and outliers, SVM tends to bias towards the majority(negative) class in an imbalanced data set and this leads to a poor classification accuracy of minority(positive) class.In this paper, an improved fuzzy support vector machine (FSVM) algorithm is proposed to deal with these problems. When designing the fuzzy membership in the new algorithm, we take into consideration not only the distance from the sample to the center of its class but also the tightness of the samples. The experimental results show that compared to the standard SVM algorithm and the other FSVM models, the new method has better performance in the imbalanced and noise-containing datasets. imbalanced datasets; FSVM; fuzzy membership degree; tightness of a sample TP18 A 10.19358/j.issn.1674- 7720.2017.16.016 陈辉辉,白治江.基于模糊支持向量机的非平衡数据分类[J].微型机与应用,2017,36(16):56-59. 2017-02-20) 陈辉辉(1992-),男,硕士,主要研究方向:信息处理与模式识别。 白治江(1962-),男,博士,副教授,主要研究方向:模式识别、人工智能。
5 实验与实验结果分析










6 结论

