改进的矢量阵常规波束形成算法

俞育新马伯乐

（1.海军舟山地区装备修理监修室舟山316000）（2.92721部队舟山316000）

改进的矢量阵常规波束形成算法

俞育新1马伯乐2

（1.海军舟山地区装备修理监修室舟山316000）（2.92721部队舟山316000）

为提高矢量阵方位估计能力，介绍一种改进的矢量阵常规波束形成算法（IVACBF）。该方法首先利用声压，振速对各向同性噪声的抑制能力，给出一种矢量阵联合信息处理法（NVACIP），并得到对应的空间功率谱；最后，与(p+vc)vc法的空间谱进行合成，实现目标的方位估计。理论分析表明，这种算法的旁瓣抑制与抗左右舷模糊能力更强，噪声影响更低。最后的仿真与实测数据证明，相比于长阵列形式的常规波束形成（LACBF）与(p+vc)vc法，IVACBF算法可以获得更低的旁瓣与更窄的主瓣，从而改善了矢量阵方位估计能力。

矢量阵；常规波束形成；左右舷模糊

Class NumberTB565.1

1 引言

波束形成是利用加权求和方法实现传感器阵列抑制干扰，增强目标信号的一种处理手段［3，12］。根据权值的不同，波束形成分为常规波束形成（CBF）与MVDR波束形成两种。该类算法由于无需对信源数的先验知识，已成为目标DOA盲估计的有效算法。

声矢量水听器是由两或三个正交的方向振速传感器与一个可选的声压传感器构成。这种结构可以使声矢量传感器同时测量某点处的声压与振速信息［4］。因此，声矢量传感器对水声信号的感知要比传统标量（声压）水听器更精确［5］。同时单个矢量水听器具有不依赖频率的单边指向性和抗各向同性噪声能力。正是由于以上这些优势，相比于声压阵，矢量阵的目标探测性能要更优越。多年来，包括声矢量阵（direction of arrival，DOA）估计在内的矢量水听器目标方位估计，已经得到了大量研究［6～13］。其中文献［12～13］充分利用了声压振速对各向同性噪声的抑制能力，提高了信噪比。特别是文献［12］在信噪比改善基础上，给出了一种声压与组合振速的数据组织形式，提高了矢量水听器的抗左右舷模糊与旁瓣抑制能力。

为了获得分辨率更高的方位估计。本文首先依据文献［12～13］的原理给出一种新的矢量阵联合信息处理法，然后将该处理法的波束形成与文献［12］的空间谱进行合成。最后无论是理论分析还是仿真与实测结果都证明，本文的改进常规波束形成具有更好的角度分辨能力与单边指向性。

2 信号接收模型与基本假设

本文的信号与噪声的基本假设为

1）本文的信号假设为远场平面波；并且不同方位信号间独立；

2）本文的噪声为各向同性噪声场；噪声满足高斯分布；

3）信号与噪声间统计独立；

4）本文阵列形式为均匀线阵；

5）本文的传感器为二维矢量水听器。

假设一个半波间隔均匀线阵，如图1所示。

阵列由N个矢量传感器构成，阵元间距为d；信号入射方向与阵列法线成θ；设k个信号，则阵列接收信号模型为

其中阵列流形A(θ)为

α(θ)为声压阵的方向矢量，对于第j个目标有：

其中：λ为信号的波长，D(θ)为单个矢量水听器的方向矢量，本文仅考虑二维矢量传感器，对于第j个目标，其值为

式（1）中信号矢量S(t)为

噪声矢量N(t)为

对于本文研究的二维矢量传感器阵列，各阵元中的振速噪声功率一致，都是声压水听器噪声功率的一半。

3 两种矢量阵常规波束形成算法

本节将介绍矢量阵长阵列形式与文献［12］的(p+vc)vc两种常规波束形成算法。

3.1 矢量阵长阵列形式CBF算法（LACBF）

LACBF算法的基本思路是按照式（1）的接收数据直接套用CBF算法得到的。首先得到式（1）的协方差矩阵：

然后进行空间搜索得到空间功率谱：

其中：β(θ)是形式与α(θj)⊗D(θj)一致的导向矢量，θ为导向角度。在功率谱图中功率值最强的导向角即为目标方位。以单个目标为例，式（8）可表达为

其中：RLACBFS为对应的信号部分协方差矩阵；P(θ)等于声压阵信号部分的空间功率谱；θd=θ-θ0为目标方位角与导引角之差；RLACBFN噪声协方差矩阵，其表达式为

谱φ(θ)为

3.2 基于联合信息处理的矢量阵CBF算法（(p+vc)vc）

文献［12］的(p+vc)vc法充分利用了声压振速通道对各项同性噪声的抑制能力，从而减少了噪声影响。本小节对该算法不再详细论述，直接给出其空间功率谱表达式。与上文一样，假设单目标情况，于是(p+vc)vc的空间功率谱为

其中：R(p+vc)vcCBFS为对应的信号部分协方差矩阵；R(p+vc)vcCBFN为对应的噪声部分协方差矩阵；η(θ)为形式与α(θj)一致的导向矢量。由本节的介绍可见，两种矢量阵常规波束形成的信号部分，实际是声压阵常规波束形成与一个方向因子的合成。为更好提高角度分辨率，下节将给出一种改进的矢量阵常规波束形成（IVACBF）。

4 改进的矢量阵常规波束形成（IVACBF）

该算法的基本思路是利用一种新的矢量阵联合信息处理法（NVACIP）得到一个空间功率谱，然后将该功率谱与(p+vc)vc算法进行合成，得到一个合成方位谱。

4.1 一种新的矢量阵联合信息处理法（NVACIP）

首先给出两个电子旋转阵列：

由式（13），（14）与声压阵得到三个协方差矩阵：

以单个目标为例，可得到式（15）各矩阵的信号部分为：

其中θd为导引角θ与真实角度的差值；Rs的表达式为

其中s为声压阵的接收信号，并且Rs的维度为N×N。而对于式（15）各矩阵噪声部分为

根据矢量阵各通道间对各向同性噪声抑制的特性，式（18）可写为

而噪声部分矩阵为0矩阵。最后对矩阵Res进行空间搜索得到NVACIP空间功率谱为

由式（26）可见，NVACIP空间功率谱也是一个由方向因子与声压阵空间功率谱的合成谱，但与式（9），（12）不同，式（26）无噪声项干扰。

4.2 改进的矢量阵常规波束形成（IVACBF）

为获得更好的方位估计效果，将NVACIP空间功率谱与(p+vc)vc功率谱进行合成得到IVACBF算法的空间功率谱为

其中上述三个噪声矩阵的维度为N×N。然后将上述的三个协方差矩阵做如下运算，得到一个矩阵为

式（24）对应的信号部分矩阵为

同理可得：

其中：GIVACBF(θ)与GNVACIP(θ)的表达式为

从式（27）可见，本文的合成空间功率谱的信号部分是一个方向因子与一个声压阵空间功率谱平方的合成，并且噪声项也受到NVACIP方向因子的调制。下节将分析本文三种矢量阵常规波束形成的性能。

5 算法性能分析与比较

为说明IVACBF算法在方位估计方面的优势，本节将从旁瓣抑制，噪声调制与抗左右舷模糊三方面分析比较三种矢量阵常规波束形成算法的性能。

5.1 旁瓣抑制能力分析

由文献［12］的分析可见，矢量阵常规波束形成优于声压阵的原因在于方向因子的调制。因此定义归一化方向因子绝对值为调制度，于是得到本文三种算法的方向因子的调制度为

仍以单目标为例，GLACBF(θ)，G(p+vc)vc(θ)的表达式为

由式（28）～式（32）可见，只有当θd=0时H1(θ)，H2(θ)，H3(θ)的值才达到1，在其余情况下都小于1，也就是说只有导引角与目标方位角一致时无调制，在其它角度时方向因子抑制了旁瓣的空间功率大小。正是由于这种额外调制作用，矢量阵常规波束形成的旁瓣低于声压阵，从而提高了角度分辨力。图2给出了本文三种方向因子的抑制度图（设目标方位90°）。

由图2可见，椭球体越窄说明抑制度越大，越有利于旁瓣的抑制。由此可见除了目标角度90°外，本文三种方向因子抑制度的关系为

同时，从式（27）可见，IVACBF信号部分的空间功率谱是方向因子与声压阵空间功率谱平方的合成，因此这又更有利于旁瓣的抑制。

5.2 噪声调制能力分析

由式（9），式（12）与式（27）的表达式可见，噪声的存在会造成旁瓣的升高，这势必影响角度的分辨力。然而，本文算法噪声可以受到NVACIP方向因子的调制。式（27）可写为

同样，通过GNVACIP(θ)绝对值归一化的表达式可见，除了导引角与方位角重合情况，其余角度处，噪声功率都会受到抑制，而另两个算法的噪声是定值。由此可见，本文的IVACBF算法可以很好的在旁瓣位置抑制对应的噪声，从而有利于角度的分辨。

5.3 抗左右舷模糊能力分析

矢量阵优于声压阵的另一个方面是抗左右舷模糊能力，仿照文献［12］的分析方法，定义左右舷模糊抑制增益为

其中：D'为模糊角度抑制度与真实角度抑制度之比。图（3）给出了目标角度为[0，360]的本文三个算法抗左右舷模糊能力示意图。

由上图可见，IVACBF算法可以在更多的角度处形成强抑制，具有更好的单边指向特性。由本节的分析可见，IVACBF算法可以得到更好的旁瓣抑制，并且对噪声影响可以起到相应的抑制力，同时具有更好的单边指向性。下节将给出相应的仿真与实测数据证明本文算法的有效性。

6 仿真与实测结果比较

为证明本文算法的有效性，本节将给出相应的仿真与实测结果比较。

仿真1本仿真将给出单目标情况下三种矢量阵常规波束形成算法的方位估计能力比较。仿真条件为：4元矢量阵；目标方位60°；信号为窄带信号；快拍数100；信噪比0db。图（4）给出了三种算法的空间功率谱图。从图中可见，相比于LACBF算法，(p+vc)vc由于噪声减小与方向因子的作用，其旁瓣更低，主瓣更窄，更有利于角度的分辨。然而本文的IVACBF算法的估计性能又更优于(p+vc)vc算法，其最低旁瓣之差为38db，高于(p+vc)vc算法10db，高于LACBF为9db。并且，从图4可见，本文算法仍具有良好的单边指向性。

半功率波束宽度（HPBW）是衡量波束形成角度分辨力的重要指标。图5给出了本文三种算法HPBW的比较图；信噪比为-8-10db，100次蒙特卡洛试验。从图5可见，(p+vc)vc算法由于噪声影响的减小在低信噪比情况下，其HPBW要小于LACBF，随着信噪比的提高，两者的HPBW都减小，然而在方向因子的作用下，(p+vc)vc的半功率波束宽度仍略小于LACBF，这与文献［12］的分析一致。然而，本文的IVACBF算法由于方向因子的作用无论在何种信噪比下，其HPBW是三种算法中最低的。由此可见，IVACBF的角度分辨力要优于LACBF与(p+vc)vc算法。

仿真2本仿真将给出双目标情况下空间功率谱图的比较结果。两个非相干目标方位为60°与105°，其余仿真条件与上文一致。图6给出了三种矢量阵常规波束形成的方位功率谱。从图中可见，IVACBF最小旁瓣差值为39db，(p+vc)vc为28db，LACBF为10db，因此本文算法在双目标情况下，其旁瓣仍然很低，并且具有较好的单边指向性。

实测数据分析：实验数据来自某次湖试，基阵是由三个二维矢量水听器构成的均匀线阵，阵元间距0.5m。采样频率96kHZ，目标信号为一个频率为1500HZ的单脉冲信号。数据长度1s，目标方位大致在130°左右。图7给出了本文三种波束形成的空间功率谱图。从图中可见，IVACBF最小旁瓣差46db，(p+vc)vc差值为28db，LACBF差值为19db。由此可见对于实测数据本文的IVACBF算法的旁瓣抑制力更强，更有利于目标角度的估计。同时，在模糊角度处，本文算法的抑制效果要优于另外两种方法。同样为更清晰比较角度分辨力，表1给出了三种算法实测数据的HPBW。由表1可见，本文的IVACBF算法的HPBW要窄于LACBF16°，同时窄于(p+vc)vc算法14°。

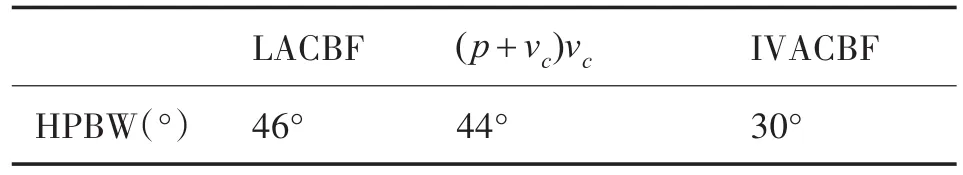
表1 HPBW值表

实测数据验证表明，本文的IVACBF算法的旁瓣更低，主瓣更窄，更有利于目标方位估计，同时具有良好的抗空间模糊能力。

7 结语

为进一步提高矢量阵方位估计能力，本文首先给出一种联合信息处理法（VACSP）然后得到对应的空间功率谱，并与(p+vc)vc算法的空间功率谱合成，实现目标的方位估计。理论分析可见，本文的这种算法具有更尖锐的方向因子抑制能力，同时由于合成的作用，可以得到声压阵空间功率谱平方，从而更进一步抑制旁瓣。而且VACSP的方向因子，对噪声具有一定的调制能力，从而减小了噪声的影响。在抗空间模糊方面，本文的IVACBF算法可以在更多的方位角上获得模糊角度的强抑制。最后的仿真与实测数据均证明了，IVACBF算法可以获得更窄的主瓣和更低的旁瓣，并且很好抑制模糊角度。因此，本文算法为矢量阵的应用提供了较有价值的参考。

［1］Harry L.Van Tress.Optimum array processing［M］.NewY⁃ork：John Wiley&Sons，Inc，2002：17-37.

［2］Zhang Y，Ye Z，Liu C.An efficient DOA estimation meth⁃od in multipath environment［J］.Signal Processing，2010，90（2）：707-713.

［3］Kumazawa T，Oka F，Kashizaki T.High accuracy DOA estimation of electromagnetic pulses using analogue signal processing［J］.IEEE Transaction on Fundamentals and Materials，2010，130（5）：514-522.

［4］Xionghu Zhong，A.B.Premkumar.Partical Filteringap⁃proaches for multiple acoustic source detection and 2-D direction of arrival estimation using a single acoustic vec⁃tor sensor［J］.IEEE Transactions on signal processing，2012，60（9）：4719-4733

［5］P.Palanisamy，N.Kalyanasundaram，P.M.Swetha Two-dimensional DOAestimation of coherent signals us⁃ing acoustic vector sensor array［J］.Signal Processing 2012，92：19-28.

［6］Nehorai A，Paldi E.Acoustic vector sensor array process⁃ing［J］.IEEE Transactions on Signal Processing，1994，42（9）：2481-2491.

［7］Abdi A，Guo H H.Signal correlation modeling in acoustic vector arrays［J］.IEEE Transactions on Signal Processing，2009，57（3）：892-903.

［8］Zou N，Nehorai A.Circular acoustic vector-sensor array for mode beamforming［J］.IEEE Journal on Signal Pro⁃cessing，2009，57（8）：3041-3052

［9］P.palanisamy，N.Kalyanasundaram，P.M.Swetha.Two-di⁃mensional DOA estimation of coherent signals using acous⁃tic vector sensor array［J］.Signal Processing，2012，92，19-28.

［10］V.N.Hari，G.V.Anand，A.B.Premkumar.Narrowband signal detection techniquesin shallow ocean by acous⁃tic vectorsensor array［J］.signal processing，2013（23）：1645-1661

［11］付金山，李秀坤.声矢量阵DOA估计稀疏分解理论研究［J］.哈尔滨工程大学学报，2013，34（3）：280-286.

［12］姚直象，余贵水，贺富强.矢量阵改进常规波束形成［J］.兵工学报，2011.32（2）：176-180.

［13］白兴宇，杨德森，赵春晖.声矢量阵远程定向技术（一）—新的协方差矩阵生成方法［J］.信号处理，2006，22（3）：374-378.

Improved Vector Array Conventional Beamforming Algorithm

YU Yuxin1MA Bole2
（1.Repair Representative Office of Navy in Zhoushan，Zhoushan316000）（2.No.92721 Troops of PLA，Zhoushan316000）

With the purpose of improving the bearing estimation capacity of vector array，this paper presented an improved vector array conventional beamforming algorithm（IVACBF）.This algorithm constructs a new processing method of vector array based on co-information（NVACIP）by suppressing noise ability of pressure and velocity；and obtains corresponding space power spectrum；then combines with(p+vc)vcto get bearing estimation of target.According to the analysis of theory，the algorithm pre⁃sented by this paper has a better sidelobe suppressing and left-right ambiguity suppressing ability and the influence of noise could be reduced.At last，the simulation and real measured data show，compared to long-array conventional beamforming（LACBF）and (p+vc)vc，IVACBF could have lower sidelobe and narrower mainlobe to improve bearing estimation capacity of vector array.

vector array，conventional beamforming，left-right ambiguity

TB565.1

10.3969/j.issn.1672-9730.2017.08.009

2017年2月10日，

2017年3月21日

俞育新，男，高级工程师，研究方向：舰载武器系统。马伯乐，男，工程师，研究方向：舰水下目标特性识别和信息感知。