赡养经济、延迟退休与经济增长——基于中国退休制度改革

张 释 文

(对外经济贸易大学 保险学院， 北京 100029)

赡养经济、延迟退休与经济增长
——基于中国退休制度改革

张 释 文

(对外经济贸易大学 保险学院， 北京 100029)

通过家庭赡养结构引入附带人力资本的世代交叠模型以探究寿命延长、赡养结构、劳动强度等因素对个人退休决策的影响。模型中强调中国等亚洲文化独有的“双向利他性”，即考虑家庭内部父辈对子女的教育投资及子女对父辈的回馈这样的赡养结构。数值模拟部分讨论了不同退休制度情况下经济增长情况的差异。个人退休决策由人均寿命、赡养依赖、劳动相对于资产的价值、折算系数和老年劳动强度的下降程度等共同决定；延迟退休会带来经济增长，而经济增长幅度随人均寿命增加而减少，随赡养依赖程度增加而增加。

赡养经济；延迟退休；弹性退休

一、引 言

随着我国人口寿命的延长、人均受教育年限的提高和养老金支付压力的增大[1]，延迟退休年龄大势所趋。2013年11月，中国共产党第十八届中央委员会第三次全体会议通过的《中共中央关于全面深化改革若干重大问题的决定》正式提出“研究制定渐进式延迟退休年龄政策”的指导性意见，拉开了退休年龄制度实质性改革的序幕。

国外对于个人退休决策及其经济效应的研究比较丰富。学者们己经就长寿、资产组合、收入以及社会保障给付等对劳动者退休年龄的影响做了丰富的理论分析和实证研究，比如，Hu[2]和Bloom[3]等通过构建连续时间一般均衡框架发现寿命延长有延迟退休的作用，从而增加个人的物质资本或者提高储蓄率；Lambrecht等构建了基于利他性的代际转移OLG分析框架，但没有考虑代际转移的动机[4]。近几年，相关研究逐步从退休决策的内涵延伸至退休制度的经济效应，Zhang等人将利他性人力资本投资引入OLG模型，认为推迟强制退休年龄将有利于长期经济增长[5]。Gustman等研究了当前经济衰退对退休年龄人口的影响，用一个结构性的退休模型模拟表明婴儿潮时期出生的人在自由选择退休年龄时更倾向于推迟退休[6]。Van和Hendrik论述了雇主对推迟退休年龄的看法，并阐述了欧盟国家鼓励提高老年人劳动参与率的原因[7]。Janine获取了荷兰老年工人对延迟退休的态度变化[8]。Gonzalez-Eiras和Niepelt从公共投资驱动型经济的视角出发，认为推迟强制退休年龄将阻碍长期经济增长[9]。

相比之下，国内研究稍显不足，且缺乏解释力。曾燕、郭延峰和张玲建立了一般均衡框架下长寿风险的两期OLG延迟退休模型，指出长寿风险暴露下延迟退休是个人最优决策，同时提出了改固定退休制度为弹性退休制度的建议[10]，但遗憾的是没有考虑人力资本投资以及退休决策的经济效应。胡仕强通过构建一般均衡框架研究长寿风险、投资组合与最优退休决策之间的关系，提出对现有养老金体制进行改革和完善，使之更有利于资本累积的建议[11]。孙佳佳和吴铮对问卷调查数据进行线性回归，证明了年龄、收入、受教育程度和工作性质等因素对个人退休决策有决定性作用，但其问题在于对关键变量的选取缺乏必要的理论依据，主观性较大[12]。

纵观国内对于退休决策的相关研究，表明在当前环境下，延迟退休符合劳动者的最优退休决策，因而学者们倾向于将大众对延迟退休的反对态度归结为非理性原因[13]。研究普遍采用国外主流框架，研究重点关注长寿、养老保险制度和人口结构等因素，却忽略了对中国传统家庭结构—赡养经济的考量。在中国这样一个家庭养老依然占重要地位的国家，赡养经济对生命周期储蓄、社会养老保险制度的替代性作用对国人的退休决策起着重要的作用。目前，国内有关赡养经济的研究比较少见，如刘庆彬和郝胜龙通过假设赡养的不确定性讨论了保险、最优投资结构和国家经济体的最优增长方式[14]。同时，现有研究对人力资本投资的关注不足，从政策层面来看，所有研究都未能详细地分析退休决策和退休制度及其对资本积累、经济增长的影响。

因而在借鉴前述研究成果的基础上，本文从中国的家庭赡养结构出发，利用经典的OLG模型，通过双向利他性假设将赡养经济引入个人退休决策分析框架，并解释其经济效应，以期对未来的退休年龄制度改革有所裨益。

二、模型建立

基于Lambrecht等[4]、Zhang和Zhang[5]、Gonzalez-Eiras和Niepelt等[9]的设定，继续采用离散时间结构，以便在其基础上扩展人力资本投资的方式并引入赡养性特征。

1.个体行为

假设模型存在无穷期，且存在无数生存3期(童年期、青年期和老年期)的同质代表性个体。每个代表性个体在童年期不参与劳动，在青年期和老年期各有一单位的劳动时间禀赋。个体以概率1从儿童期成长到青年期，以概率1在青年期养育一个孩子，但从青年期到老年期存活概率为p∈(0,1)，p值的增加代表死亡率下降或者预期寿命的延长。为简化分析，假设人口测度为1，则任意时点的总人口为:2+p[5]。

假设个体在青年期和老年期均面临实物消费C和闲暇消费L的分配，其权衡取决于个体对于闲暇的偏好程度，用闲暇系数η(0,1)表示。在老年期，代表性个体自由选择退休时间，用ρ表示个体进入老年时期后继续供给劳动力的时间，则1-ρ为退休时段，存活至老年期的个体的退休年龄为2+ρ。通过这种方式定义退休有着现实的考量：一般情况下，个体在青年时期能够承受的劳动强度普遍较高，但是在老年期则往往由于身体的衰弱使得劳动强度下降(用折算系数λ表示残留的劳动能力)，当劳动强度下降至无法满足任何工作需求时退出劳动力市场。

在模型中，经济的赡养性特征体现为“双向反复博弈”，即青年期个体对后代和父辈具有双重利他性。

2.人力资本

涉及人力资本投资的相关研究大致可分为两类，一类是利己性投资[15]，教育投资的目的在于增加代表性个体本身后期的收入，因利己性的教育投资而损失的工资收入在人生的后期将得到补偿；另一类是利他性投资[5]，父代由于利他性而对孩子的人力资本进行投资，父代的人力资本投资无法得到补偿。首先，纯粹的利己性投资并不符合中国的现状[16]，同时，现有文献中利他性投资动机并不全面，这种文化概念的背后是寄希望于后代可以奉养老年期的自己，也就是所谓的“养儿防老”[17]，因而利他性投资同样可以得到补偿，其动机在于赡养经济。根据王跃生的观点，中国有大约39%的家庭依靠家庭赡养关系，本文的假设符合实际意义，对后代人力资本进行的投资和向后代索取赡养费用的权衡是赡养经济的关键因素[18]。

从赡养经济的角度出发，假设人力资本投资兼具利他性和利己性，利他性体现为父辈将对后代进行的人力资本投资将提高后代的收入水平，且后代的收入水平将进入父辈的效用函数。利己性体现为两个方面：一是赡养经济——老年人口将按照自身需求向成年的后代索取赡养费用；二是人力资本投资具有扩散效应，人力资本投资提高青年人人力资本的同时，随着社会平均人力资本的提高，父辈的人力资本也会随之增长[19]，投资不仅能提高后代的收入水平，同时也能提高父辈在老年期的工资水平。

借鉴Becker、Murphy和Tamura、杨建芬[16]的研究，假设任意一期的社会平均人力资本水平取决于上一期父辈对子代的教育投资和上一期的人力资本水平。本文选择Cobb-Douglas生产技术作为上一期人力资本和教育投资组合生成下一期社会平均人力资本的方式，即：

(1)

3.物质资本

现有一个资本市场将储蓄投资于物质资本，在青年期，个体将为满足老年期的消费进行生命周期储蓄，储蓄St进入资本市场后以物质资本Kt的形式投入生产。投资基金将储蓄St投资于生产部门并在下期得到Rt+1St的收益，其中R代表本利率。假设年金市场完全竞争，则年金基金将维持在0利润，所有能够活到老年的个体将得到储蓄St产生的投资收益Rt+1St/p。Rt+1/p即为家庭每单位投资的回报率，当利率一定时，投资收益率与生存率成反比，即生存率上升会使资产收益下降。

4.最优个体行为

假设代表性个体的效用函数采用对数形式，代表性个体的最大化问题可以表述为：

MaxUt=lnCt+ηlnLt+βp[lnDt+1+ηln(1-ρ(1-Lt+1) ) ]+γlnIt+1

(2)

S.T.It=(1-Lt)Wtht-Bt=Ct+Et+St

(3)

Dt+1=(Rt+1St)/p+(1-Lt+1)Wt+1ht+1ρλ+Bt+1

(4)

It+1=(1-Lt+1)Wt+1ht+1-Bt+1

(5)

由(1)～(5)可以得到最优的个体行为。其中，Ct表示t期青年个体的实物消费，Lt表示t期的闲暇，η为对闲暇的偏好，β为折算系数，1-ρ(1-Lt+1)表示老年期的总闲暇，It表示t期青年的可支配收入，由于青年收入的一部分将按老年人的需要作为赡养费一次性交付给老年人，因此，γ实际上作为赡养系数衡量了老年人对于赡养经济的依赖程度。Wtht为有效工资，(1-Lt+1)Wt+1ht+1ρλ代表老年期所能获得的总工资收入。Bt和Bt+1分别为青年人向老年人支付的赡养费和老年人收到的赡养费。其中，(1)式显示了存在赡养经济和不存在赡养经济两种情况。代表性个体效用最大化的一阶条件如下：

(6)

(7)

(8)

(9)

将(9)带入(8)可得：

(10)

(10)式表明，当存在赡养经济时，教育投资的回报率等同于对实物投资的回报率；当不存在赡养经济时，教育投资的回报率小于实物投资的回报率。这意味着赡养经济构成了人力资本投资的动力，赡养经济的存在使得父辈与后代存在着双向重复博弈的关系，即父辈由于对后代具有依赖性，从而具有增加后代收入(对后代进行人力资本投资)的动机，因而在生命周期的实物投资和人力资本投资之间存在取舍；但当不存在赡养经济时，人力资本投资的收益率将会低于物质资本投资，父辈就失去了对后代进行人力资本投资的动机。

5.生产方式

假设经济体仅生产单一的同质商品，并采用Cobb-Douglas生产函数描述物质资本和人力资本参与生产的过程：

Y=FKδH1-δ,F>0

(11)

其中，δ代表生产中资本的份额，F为技术水平。其中，H为考虑人力资本和人口死亡率的有效总劳动力供给，满足：

Ht=(1+pρλ)(1-Lt) ht

(12)

通过最大化企业的利润可以得到生产的边际条件：

(13)

(14)

其中，kt为人均有效资本存量。可以知道，劳动力市场、资本市场和产品市场的均衡条件为：

Kt=St-1

(15)

Yt=Ct+St+Et+Dt

(16)

于是得到青年期的可支配收入和老年期人口的消费：

(17)

(18)

即延迟退休对青年期的可支配收入和老年期人口的消费都有增加作用，其中，老年期人口在面临死亡时，经过理性考虑选择把所有收入都花掉，即老年期的花费也就是老年期人口的可支配收入。青年期人口可支配收入与老年期人口可支配收入加总得到社会全部生产总值，即在一定范围内单纯考虑延迟退休有利于经济增长。

三、动态均衡

1.最优退休决策

首先，寻找最优退休决策的显式解，并分析其决定因素。结合(3)、(13)、(17)得到退休时点：

(19)

即代表性个体最优退休时点由生存概率p、赡养性特征γ、有效劳动的相对价值1-δ、折算系数β和老年劳动强度的下降程度λ共同决定。值得注意的是，与Zhang等人的研究不同，上式中并未出现个体对闲暇的偏好因素η，这主要是因为Zhang等人的研究将老年的闲暇等同于退休时段[5]，而本文除了将闲暇假设为退休时段外，还假设闲暇存在于青年期和老年期劳动力供给期间，因而老年劳动力供给对闲暇不敏感。

由(19)可知，个人最优退休年龄随经济的赡养性特征的增大而下降，赡养经济将带来提前退休。赡养经济对退休决策的影响包含3个方面：由人力资本投资引致的老年工资的增加会延迟退休；赡养费用的增加对老年劳动力供给有替代作用，老年人对子女赡养的依赖越强烈越不愿意延迟退休，社会上对延迟退休的抵触情绪将越大；根据现阶段我国人力资本投资的水平和人口结构，延迟退休将成为大势所趋。

个人最优退休时点随生存率的增大而延迟，长寿将带来延迟退休，这与一系列有关长寿与延迟退休的相关研究[10]的结论一致；人口预期余命的增加，老年期人口的死亡率下降，仅靠子女赡养不足以维系老年人原有生活水平，寿命的延长会迫使老年人工作更长时间。个人最优退休时点随人力资本的相对价值1-δ的增大而延迟，高工资将带来延迟退休；这一结论与日本现在的情况相符，年龄越大代表经验越丰富，体现在模型中老人的人力资本相对价值就大于年轻人，老年人的高工资对年轻人有挤出效应。个人最优退休时点随老年人劳动强度λ的增加而前移，老年人劳动能力的增加带来提前退休。老年人劳动强度λ的增加从而使老年期获得的总工资增加，当工资的增加额刚好可以覆盖老年人由于寿命延长而增加的生活费用时，老年人选择退出劳动力市场。

2.平衡增长路径

求解动态最优得到该经济的平衡增长路径及均衡时kt的表达式：

(20)

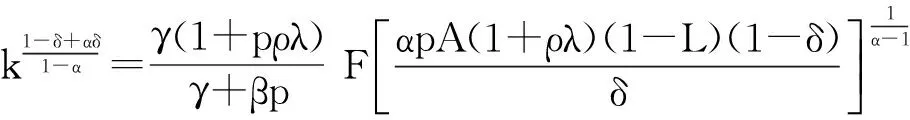
(21)

通过均衡时kt的表达式可以得到均衡消费、均衡储蓄、均衡人力资本投资等借以描绘该经济在均衡时的状态，数值模拟部分主要用到(21)式，其他不做赘言。

四、数值模拟

表1为ρ由效用最大化均衡决定的值变动至强制规定ρ=0.2时经济的增长情况，其中负数代表经济开始出现负增长。总体而言，相较于自由退休制度，强制退休制度导致人均产出减少。横向比较来看，随着p的增大强制退休导致人均产出下降，经济衰退且产出下降的幅度越来越大。ρ=0.2代表严格强制退休即退休年龄较早，可见随着人们预期余命的延长，严格强制退休制度对经济的扭曲作用越大。随着赡养性特征γ的变大，强制退休对人均产出的负面影响越来越小。在γ足够大时，p足够小的情况下，经济甚至出现正增长趋势。以2015年我国人口平均寿命76岁为参照，生存概率大致为0.81，相较于非强制性退休，强制退休制度下人均产出增长为负，即经济衰退。人均产出下降的幅度随寿命延长而增加，随赡养依赖程度增加而减少。

由表2延迟退休的经济效应可知，ρ由0.2到0.7时人均产出的变化情况，即延迟退休情境下经济的变化情况。整体而言，相较于严格强制退休制度，延迟退休后人均产出增长为正，即延迟退休促进经济增长。随着p的逐渐增大，人均产出增量逐步降低，但仍可维持在14%至15%左右。随着γ的增加，人均产出增幅不断扩大。延迟退休会带来经济增长，增长幅度随寿命增加而减少，随赡养依赖程度增加而圹大，在我国平均寿命范围内，延迟退休带来的经济增幅在15%左右。

表1 严格强制退休制度下稳态人均产出变化率

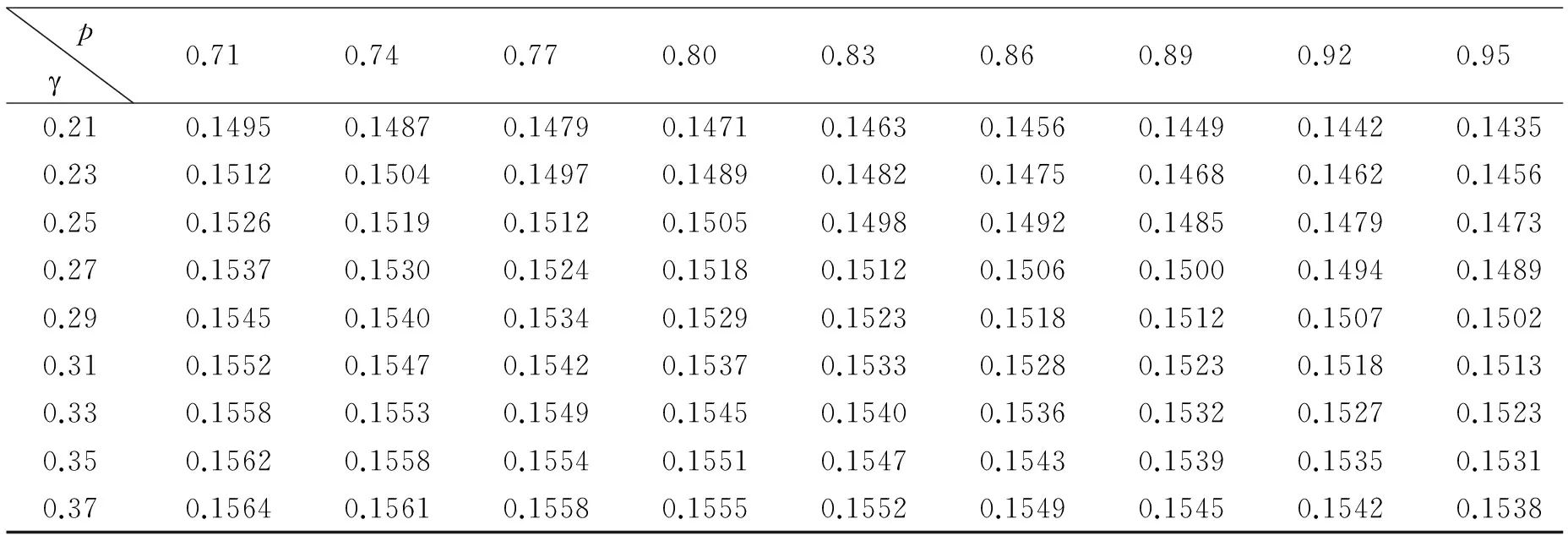
表2 延迟退休的经济效应

五、结 论

本文的主要结论有两个：(1)个人退休决策由人均寿命、赡养依赖、劳动相对于资产的价值、折算系数和老年劳动强度的下降程度共同决定；(2)延迟退休会带来经济增长，经济增长幅度随寿命增加而减少，随赡养依赖程度增加而增加。

从OLG模型部分可知随着人均寿命的延长，延迟退休将成为必然。老年期人口的死亡率下降，仅靠子女赡养不足以维系老年人原有生活水平，寿命的延长会迫使老年人工作更长时间。但在高赡养依赖的国家，老年人对子女赡养的依赖越高越不愿意延迟退休，社会上对延迟退休的抵触情绪越大。首先“养儿防老”可能成为退休制度改革的阻力，建议在推行退休制度改革的同时完善我国的社会保障制度，发展社会养老，鼓励护理医疗、临终关怀、社区养老、养老服务时间银行[20]等养老服务建设与完善，使老年人不必惧怕“老无所依”，同样可以安享晚年，减少对子女的赡养依赖。同时应着眼于改变传统观念，现今社会老龄化持续深化，高龄劳动力与青年劳动力同样重要。鼓励老年人积极参加企业培训，掌握新技术新方法，更好满足岗位需求，从根本上改变老年人的退休观念。

其次，个人最优退休时点随人力资本的相对价值的增大而延迟，高工资将带来延迟退休。因而建议在推行延迟退休制度的同时可以适当提高延迟期间老年人的工资待遇，使老年人享受投资收入的同时也不放弃劳动收入。但同时应注意老年人高工资对青年劳动力的挤出效应，对此从支持教育投资、改善人力资本投资结构、鼓励青年人创业等方面进行改善。

最后，数值模拟的结果可以证明我国延续千年的家庭养老传统实际上是有利于经济发展的，宣传弘扬我国的传统文化，增强青年人的家庭责任感有利于我国的社会建设和经济发展。

[1] 潘锦棠. 提高退休年龄不能成为弥补养老金“缺口”的主要手段[N]. 上海企业, 2012-12-24(01).

[2] HU S C. Demographics, productivity growth and the macroeconomic equilibrium[J]. Economic Inquiry,1995,33(4):592-610.

[3] BLOOM D E,CANNING D,GRAHAM B. Longevity and life-cycle savings[J]. The Scandinavian Journal of Economics,2003,105(3):319-338.

[4] LAMBRECHT S,MICHEL P,THIAULT E. Capital accumulation and fiscal policy in an OLG model with family altruism[J]. Journal of Public Economic Theory,2006,8(3):465-486.

[5] ZHANG J,ZHANG J S. Longevity, retirement, and capital accumulation in a recursive model with an application to mandatory retirement[J]. Macroeconomic Dynamics,2009,13(3):327-348.

[6] GUSTMAN A L,STEINMEIERT L. The social security early entitlement age in a structural model of retirement and wealth[J]. Journal of public Economics,2005,89(2):441-463.

[7] HENDRIK P V D,HENKENS K,SCHIPPERS J. Dealing with older workers in Europe:acomparative survey of employers attitudes and actions[J]. Journal of European social policy,2009,19(1):47-60.

[8] Dam V K,VORST J V D,BEATRICEIJM,etal. Employees intentions to retire early:a case of planned behavior and anticipated work conditions[J]. Journal of Career Development,2009,35(3):265-289.

[9] GONZALEZ-EIRAS M,NIEPELT D. Ageing, government budgets,retirement,and growth[J]. European Economic Review,2012,56(1):97-115.

[10] 曾燕,郭延峰,张玲. 基于长寿风险与 OLG 模型的延迟退休决策[J]. 金融经济学研究,2013,28(4):83-93.

[11] 胡仕强. 长寿风险,投资组合与退休决策[J]. 财经论丛，2013，(1):54-60.

[12] 孙佳佳,吴铮. 个人退休决策的影响因素研究[J]. 湖北社会科学,2009,(5):51-54.

[13] 李青. 渐进式延迟退休年龄政策研究[J]. 桂海论丛,2014,30(2):122-125.

[14] 刘庆彬,郝胜龙. 利用世代交叠模型对赡养经济中养老不确定性问题的理论研究[J]. 统计研究,2011,28(10):84-90.

[15] ECHEVARRIA C A. Life expectancy, schooling time, retirement, and growth[J]. Economic Inquiry,2004,42(4):602-617.

[16] 杨建芳,龚六堂,张庆华. 人力资本形成及其对经济增长的影响[J]. 管理世界,2006,(5):10-18.

[17] BOLDRIN M,JONES L E. Mortality, fertility, and saving in a Malthusian economy[J]. Review of Economic Dynamics,2002,5(4):775-814.

[18] 王跃生.中国家庭代际关系的理论分析[J]. 人口研究, 2008,4(1)：13-21.

[19] 杨丹妮,文雁兵. 利己动机,利他偏好与包容性增长——嵌入“家长式利他”的 OLG 模型分析[J]. 浙江社会科学,2013，(12):37-43.

[20] 张晨寒,李玲玉. 时间银行:居家养老服务模式的新探索[J]. 河南师范大学学报(哲学社会科学版)，2016，(5)：80-85.

Family Support Economy, Delayed Retirement and Economic Growth——Based on China’s Retirement Reform

ZHANG Shiwen

( School of Insurance, University of International Business and Economics, Beijing 100029, China )

Based on the overlapping-generations with altruistic individuals model, this paper tries to explain the factors affecting the timing of retirement, such as life expectancy, family support structure and labor productivity. The model highlights the importance of “Two-side Altruism” in Chinese and other Asian cultures,parents invest in children’s education and children return the kindness by supporting their parents.The data simulation demonstrates the economic growth under different retirement systems. Individual retirement timing is determined by longevity, family support structure, share of labor, time discount and relative labor productivity of the old. Moreover, delayed retirement will increase the economic growth rate, which declines with the increasing longevity but increases with the growing family support.

family support economy; delayed retirement; flexible retirement

10.19525/j.issn1008-407x.2017.03.008

2016-10-09;

2016-12-06

国家留学基金委资助项目(201506640020)

张释文(1989-)，女，辽宁大连人，对外经济贸易大学保险学院博士研究生，主要从事风险管理、劳动经济学研究，E-mail：shi_wen_zhang@yeah.net。

F243

A

1008-407X(2017)03-0055-06