较大雷诺数下方柱绕流的数值模拟

肖 姚， 秦 浩,2， 宋文武,2， 胡 帅

(1．西华大学 能源与动力工程学院，成都 610039；2．西华大学 流体及动力机械教育部重点实验室，成都 610039)

较大雷诺数下方柱绕流的数值模拟

肖 姚1， 秦 浩1,2， 宋文武1,2， 胡 帅1

(1．西华大学 能源与动力工程学院，成都 610039；2．西华大学 流体及动力机械教育部重点实验室，成都 610039)

基于k-ωSST模型和γ-Reθ转捩模型，分析了雷诺数为1.4×104和2.2×104时二维方柱的流场特征，计算方柱的阻力系数和斯特劳哈尔数Sr，并对方柱平均流场的速度剖面进行分析，综合考虑不同湍流模型的计算成本及计算精度.结果表明：γ-Reθ转捩模型比k-ωSST模型计算结果更加精确且所需计算成本较小；γ-Reθ转捩模型能较好地预测方柱尾缘近壁回流区的位置和大小，且能较好地观测流场在方柱尾缘的再附着现象;在求解实际大雷诺数工程问题中γ-Reθ转捩模型为优秀的湍流模型.

方柱绕流； 数值模拟； 阻力系数； 湍流模型； 时间步长

钝体绕流广泛存在于流体机械、动力工程和石油工程等领域中，如汽轮机叶片、换热器管群及海洋钻井平台等均涉及钝体绕流问题.钝体绕流所引起的振动会造成设备工作不稳定，当振动频率与结构的固有频率相接近时会产生共振，影响结构的使用性能，振动严重时甚至会对结构造成破坏性损坏.方柱绕流存在复杂的涡结构，而涡的脱落对于方柱所受的升力和阻力均有较大影响.因此，深入研究方柱绕流对解决工程实际中相关问题有着重要意义.

为了准确高效地计算出方柱流场的分布以及了解涡的形成与脱落规律，很多学者对方柱绕流开展了研究工作[1-10].如Durao等[1]在水洞中利用多普勒激光测速仪(LDV)研究了方柱在雷诺数为1.4×104时的绕流问题，结果表明随着湍流的波动，在颤振速度最大区域的能量可达总能量的40%.Lyn等[2]基于LDV实验测试了雷诺数为2.2×104时方柱的流场，得出方柱尾缘的速度分布规律以及涡的分布与大小.张伟等[3]采用粒子图像测速仪(PIV)和k-ωSST模型研究了雷诺数为2.2×104时的方柱绕流流场，得出k-ωSST模型计算结果与实验数据吻合较好.Bouris等[4]利用大涡模型数值模拟了小雷诺数(Re=250)时的二维方柱绕流，通过优化网格质量得出二维方柱的大涡模拟结果与实验数据吻合较好.梁思超等[6]基于分离涡(DES)模型研究了雷诺数为4×104时方柱绕流中马蹄涡系统的发展过程.Franke等[7]采用k-ε涡黏模型和雷诺应力模型研究了雷诺数为2.2×104时的二维方柱流场,结果表明2种模型均不能较好的与实验结果吻合.谢志刚等[8]基于大涡模型,利用精细的边界研究雷诺数为2.2×104时的方柱绕流，其结果可以媲美密网格的结果.

研究者们从实验、数值模拟和理论分析3个方面同时研究了方柱的流场，然而实验结果与数值模拟还存在一定的差异.文献[7]的研究结果与实验结果相差较大，k-ε涡黏模型计算出的Sr和阻力因数CD均偏小；文献[3]的结果虽然与文献[2]的实验结果吻合较好，但其计算结果与实验结果在近方柱的尾流区存在一个明显的跳跃，其对尾流区未能准确预测；文献[4]的计算结果较好，但计算的雷诺数较小且由于该湍流模型计算成本较高，将其应用在实际工程中不现实.实际工程多涉及大雷诺数下涡街的形成与脱落，为此需在考虑成本的情况下得出适合于工程大雷诺数的湍流模型.γ-Reθ转捩模型[11]基于k-ωSST输运方程、间歇系数γ方程和动量厚度雷诺数Reθt方程，相比k-ωSST模型，该模型可以较好地捕捉流场分离过程和湍流强度的变化.笔者基于Fluent软件分析方柱在不同Re下的流场，通过对比分析方柱的Sr、阻力系数CD、升力系数CL和流场的速度剖面等参数来对比不同湍流模型的评估结果.

1 数值方法

1.1 控制方程

二维黏性不可压牛顿流体运动的基本控制方程为连续性方程和Navier-Stokes方程：

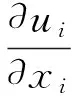
(1)

(2)

1.2k-ωSST模型

k-ωSST模型基于Menter[12]研究成果,该湍流模型在多种流态下较standardk-ω和BSLk-ω湍流模型更加精确和可靠，其表达式如下：

Gk-Yk+Sk

(3)

Gw-Yw+Dw+Sw

(4)

式中：Gk、Gw分别代表湍动能和w的产生；Γk、Γw分别为k和w的有效扩散率；Yk、Yw分别为由湍动产生的耗散率；Sk、Sw为源项.

1.3γ-Reθ转捩模型

Menter等[11]提出了γ-Reθ转捩模型，该湍流模型由k-ωSST输运方程、间歇系数γ方程和动量厚度雷诺数Reθt方程组成，其中间歇系数γ用来描述边界层的状态，并控制过渡点下游湍动能的生成项，式(5)为间歇系数无量纲输运方程的守恒形式.动量厚度雷诺数Reθt通过捕获非局部影响的湍流强度来控制由边界层内间歇系数的增长和当地涡量雷诺数构成的转捩触发准则，其表达式如下：

(5)

(6)

式中：μt、σθ、σγ为模型系数;Pγ1、Eγ1代表转捩源项;Pγ2、Eγ2分别为破裂系数和再附着系数;Pθ为源项.

1.4 方柱几何模型与网格划分

图1 方柱流场计算域

图2 网格划分

采用Fluent软件进行数值模拟，设定初始条件:u1=U0，u2=0；方柱入口定义为速度边界条件，来流为均匀速度U0；出口定义为自由流边界条件，方柱壁面与计算域边界定义为无滑移壁面.

2 结果与讨论

2.1 湍流模型对比

首先以文献[1]和文献[2]的实验结果作为数值模拟的参照对象，计算不同Re下各湍流模型最佳的模拟时间步长，得出方柱阻力系数和升力系数的时程曲线，将升力系数时程曲线进行快速傅氏变换(FFT)得到涡街脱落频率f.其中阻力系数CD、升力系数CL及Sr的定义分别为：

(a) 方柱上壁面Y+

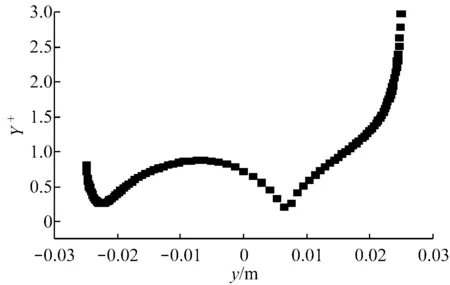
(b) 方柱尾缘壁面Y+

(7)

式中：FD和FL分别为方柱所受的阻力和升力.

表1 不同Re下方柱绕流的Sr和

(a) k-ω SST模型

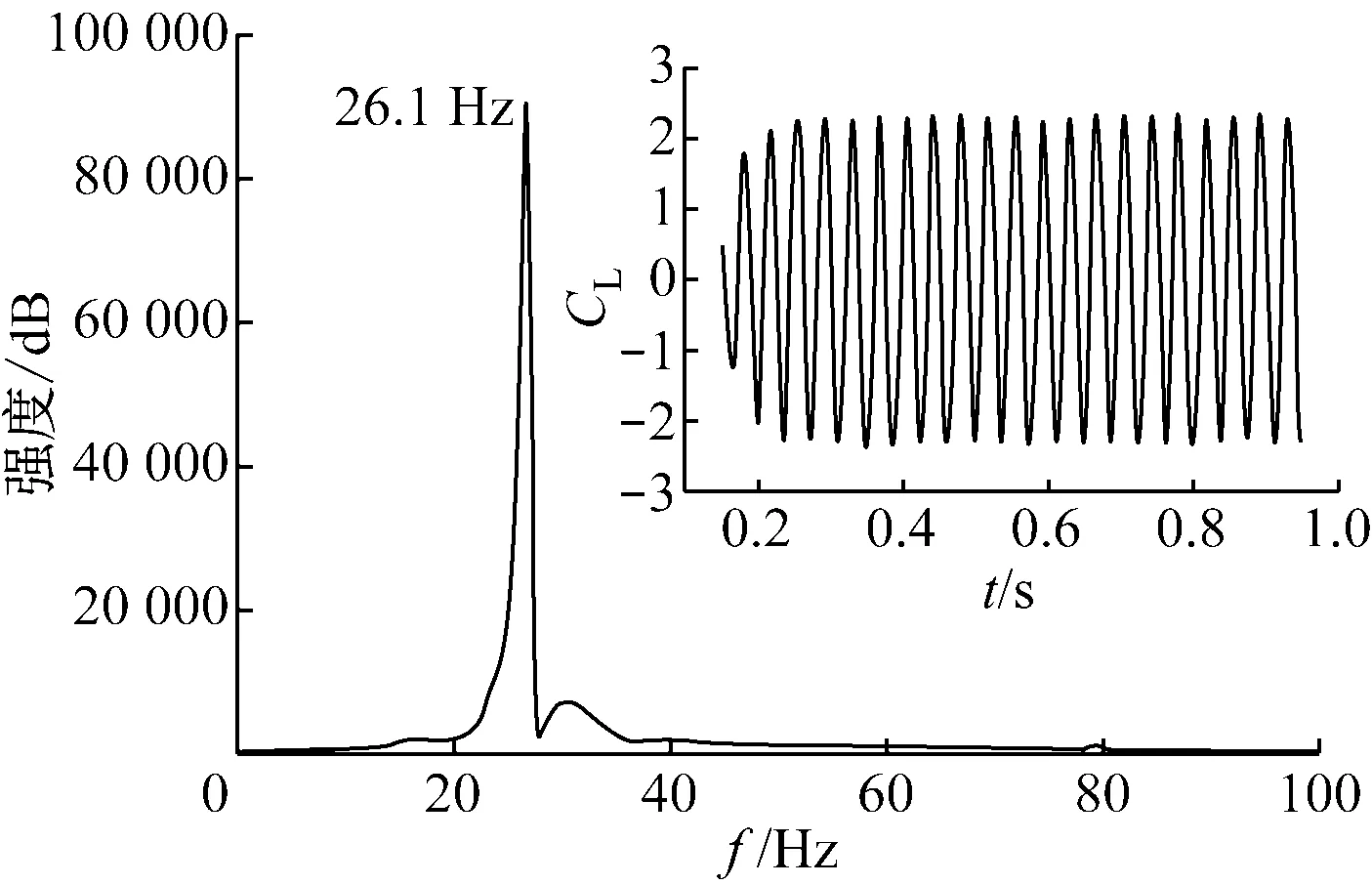
(b) γ-Reθ转捩模型

2.2 流场分析

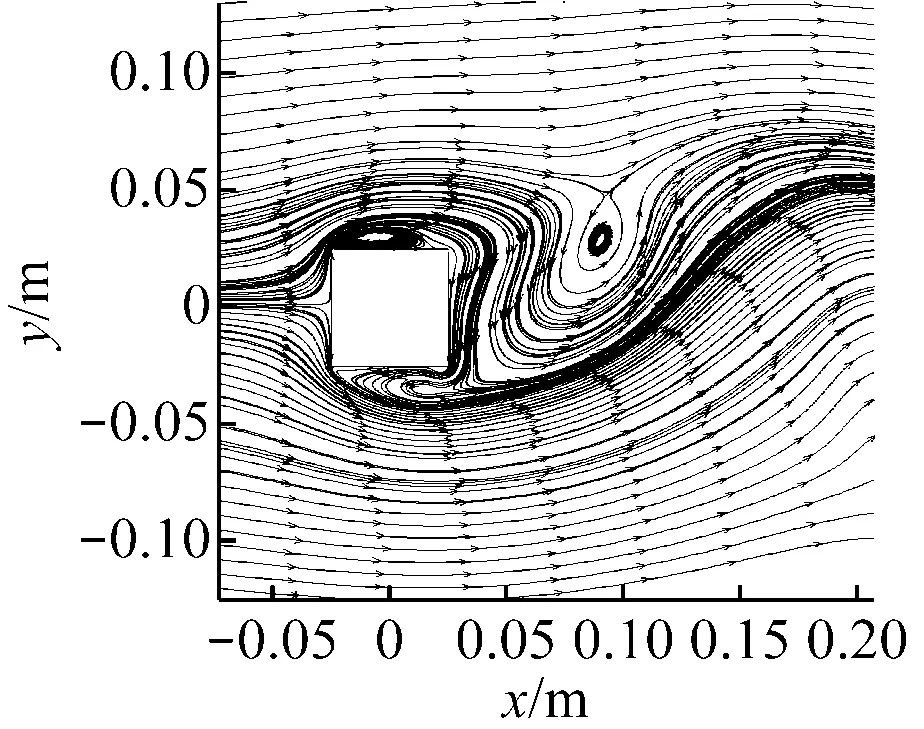
由第2.1节可知γ-Reθ转捩模型可以较好地评估实际工程大Re下的流场变化，为了与实验进行对比，下文只分析Re为2.2×104时方柱尾缘涡的脱落过程.图5为方柱平均流场速度分布曲线与水平湍动能变化曲线.从图5(a)可以看出，2种湍流模型计算结果在方柱前缘的速度场与文献[1]的实验结果吻合.在1.8

(a) 水平速度剖面

(b) 竖向速度剖面

(c) 水平剖面湍动能

综上，γ-Reθ转捩模型与三维大涡模拟结果以及实验结果较为接近，但由于尾流近壁回流区是三维流动，本文结果还存在一定的偏差.

2.3 尾涡脱落

由表1可知，雷诺数为2.2×104时采用γ-Reθ转捩模型计算得出的方柱涡脱落频率为17 Hz，周期为0.059 s.图6给出了Re为2.2×104时方柱尾缘涡脱落的半个周期过程，其中τ为时间.从图6可以看出，在方柱前缘-0.05 m左右流场开始分离，并在方柱两侧产生回流区，在方柱尾缘也有短暂再附着现象.在这半个周期内尾涡从方柱尾缘上方逐渐形成，并在尾缘扩大，在一定程度时涡开始脱落，其形成尾涡的大小与方柱的特征长度相近.

(a) τ=0 s

(b) τ=0.000 2 s

(c) τ=0.000 4 s

(d) τ=0.000 6 s

(e) τ=0.000 8 s

(f) τ=0.001 s

(g) τ=0.001 2 s

(h) τ=0.001 4 s

(i) τ=0.001 6 s

(j) τ=0.001 8 s

图6 方柱尾涡脱落过程

Fig.6 Shedding process of vortex from the square cylinder

3 结 论

(1) 与其他湍流模型相比，γ-Reθ转捩模型可以精确地评估大Re下方柱的Sr、CD和CL.

(2) 与相关实验结果对比，γ-Reθ转捩模型与实验结果的速度剖面吻合较好，可以较好地预测方柱尾缘回流区的大小和位置，计算结果与三维大涡模拟结果较为接近.

(3)γ-Reθ转捩模型可以准确地分析方柱壁面涡的形成与脱落过程以及流场再附着现象，很好地揭示了绕流的流动机理.

[1] DURAO D, HEITOR M V, PEREIRA J C F. Measurements of turbulent and periodic flows around a square cross-section cylinder[J]. Experiments in Fluids, 1988, 6(5): 298-304.

[2] LYN D A, EINAV S, RODI W, et al. A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder[J]. Journal of Fluid Mechanics, 1995, 304: 285-319.

[3] 张伟, 葛耀君. 方柱绕流粒子图像测速试验与数值模拟[J]. 同济大学学报(自然科学版), 2009, 37(7): 857-861, 892.

ZHANG Wei, GE Yaojun. Particle image velocimetry study and numerical simulation of turbulent near wake of square cylinder[J]. Journal of Tongji University(Natural Science), 2009, 37(7): 857-861, 892.

[4] BOURIS D, BERGELES G. 2D LES of vortex shedding from a square cylinder[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 80(1/2): 31-46.

[5] 李慧君, 王炯. 基于水平圆管外加装排液板降膜流动的数值模拟[J]. 动力工程学报, 2016, 36(4): 265-270.

LI Huijun, WANG Jiong. Numerical simulation of falling film flow on horizontal circular tubes with drainage strips[J]. Journal of Chinese Society of Power Engineering, 2016, 36(4): 265-270.

[6] 梁思超, 张晓东, 康顺, 等. 方体绕流的DES模拟及其旋涡结构分析[J]. 工程热物理学报, 2015, 36(3): 535-540.

LIANG Sichao, ZHANG Xiaodong, KANG Shun, et al. DES simulation of the flow around a cube and analysis of the vortex structure[J]. Journal of Engineering Thermophysics, 2015, 36(3): 535-540.

[7] FRANKE R, RODI W. Calculation of vortex shedding past a square cylinder with various turbulence models[M]//DURST F, FRIEDRICH R, LAUNDER BE, et al. Turbulent Shear Flows 8.Berlin Heidelberg:Springer, 1993.

[8] 谢志刚, 许春晓, 崔桂香, 等. 方柱绕流大涡模拟[J]. 计算物理, 2007, 24(2): 171-180.

XIE Zhigang, XU Chunxiao, CUI Guixiang, et al. Large eddy simulation of flows around a square cylinder[J]. Chinese Journal of Computational Physics, 2007, 24(2): 171-180.

[9] OKAJIMA A. Strouhal numbers of rectangular cylinders[J]. Journal of Fluid Mechanics, 1982, 123: 379-398.

[10] SAMANI M, BERGSTROM D J. Effect of a wall on the wake dynamics of an infinite square cylinder[J]. International Journal of Heat and Fluid Flow, 2015, 55: 158-166.

[11] MENTER F R, LANGTRY R B, LIKKI S R, et al. A correlation-based transition model using local variables—Part I: model formulation[J]. Journal of Turbomachinery, 2006, 128(3): 413-422.

[12] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605.

[13] BREUER M, POURQUIÉ M. First experiences with LES of flows past bluff bodies[C]//Proceedings of the 3rd International Symposium of Engineering Turbulence Modelling and Measurements. Amsterdam,Holland:Elsevier,1996: 177-186.

[14] SAHA A K, MURALIDHAR K, BISWAS G. Experimental study of flow past a square cylinder at high Reynolds numbers[J]. Experiments in Fluids, 2000, 29(6): 553-563.

Numerical Simulation of the Flow Around a Square Cylinder at Higher Reynolds Numbers

XIAOYao1,QINHao1,2,SONGWenwu1,2,HUShuai1

(1.School of Energy and Power Engineering, Xihua University, Chengdu 610039, China; 2. Key Laboratory of Fluid and Power Machinery, Ministry of Education, Xihua University, Chengdu 610039, China)

Based on thek-ωSST model andγ-Reθtransition model, a study was conducted on the flow characteristics around a square cylinder respectively at the Reynolds number of 1.4×104and 2.2×104, so as to calculate the drag coefficient and Strouhal number of the square cylinder, analyze its average velocity profiles, and finally to find out the calculation cost and precision of different turbulent models. Results show that compared withk-ωSST model, theγ-Reθtransition model is more superior in calculation precision and cost, which is more effective in predicting the position and magnitude of the recirculation region behind the square cylinder, and in analyzing the reattachment of separated flows on side walls near the rear corner, and therefore is a practical model for engineering applications at high Reynolds numbers.

flow around square cylinder; numerical simulation; drag coefficient; turbulent model; time step

1674-7607(2017)08-0679-06

O357

A

470.10

2016-08-04

2016-10-24

流体及动力机械教育部重点实验室开放基金资助项目(szjj2016-003);西华大学自然科学重点基金资助项目(Z1510418);国家自然科学基金资助项目(51408505)

肖 姚(1990-)，男，四川资阳人，硕士研究生，研究方向为流体机械. 秦 浩(通信作者)，男，讲师，博士，电话(Tel.)：13547904041;E-mail:qh.email.@foxmail.com.