基于反向传播算法的崇阳溪流域洪水流量预报

金保明，李 芸，张 烜，高兰兰，周传争，付晓雷

(1.福州大学土木工程学院，福建福州350116；2.云南省水文水资源局，云南昆明650106)

基于反向传播算法的崇阳溪流域洪水流量预报

金保明1，李 芸2，张 烜1，高兰兰1，周传争1，付晓雷1

(1.福州大学土木工程学院，福建福州350116；2.云南省水文水资源局，云南昆明650106)

基于反向传播算法原理，采用试错法确定BP模型的隐含层节点数，并加入动量项，选取崇阳溪流域建阳水文站洪水流量过程及其上游武夷山水文站、支流麻沙水文站相应洪水流量过程资料，同时考虑建阳站前期流量的自回归影响，建立建阳站最速下降动量反向传播洪水流量预报模型。计算结果表明，模型预测精度符合要求，可以作为流域预测洪水的方法之一，为流域防汛会商和指挥调度提供依据。

洪水预报；流量；BP算法；神经网络

河道洪水预报是一个比较复杂的问题，除了采用传统的预报方法外，也可采用反向传播算法建立非线性的神经网络洪水预报模型进行预报。神经网络应用于洪水预报的初期，一般是对最基本的反向传播网络直接应用。之后，有人针对反向传播算法存在的问题提出改进的方法，包括自适应调整学习率法[1]、附加动量法[2]、弹性BP算法[3]、LM算法[4]等。基于反向传播算法的神经网络由于其具有良好的自组织性、自适应性和容错性，为非线性系统的建模和预测提供了方便，在洪水流量预报方面具有独特的优势。例如，戴会超等[5]建立了具有洪峰识别的宜昌站洪水流量过程反向传播模型；Qing Hua Luan等[6]基于反向传播算法，依据上游沙县、洋口、七里街的流量与区间雨量建立了十里庵洪水预报模型；陈田庆等[7]寻求基于反向传播神经网络的马斯京根模型参数动态估计方法；胡健伟等[8]设计出基于反向传播算法的洪水预报模型；韩通等[9]提出引入K最近邻算法用于洪水预报实时校正并采用BP算法实时校正，结果表明前者对确定性系数改善最优，后者对洪峰误差校正更精确；Liu Wen-Cheng等[10]采用反向传播算法和遗传算法神经网络对台湾北部淡水河的水位进行预测，均取得较好的效果。因此，反向传播神经网络应用于流域洪水预报的效果较好，适用性比较强。本次采用最速下降法并加入动量项修正权值与偏置值，建立流域反向传播洪水预报模型，并以崇阳溪流域为实例进行研究。

1 最速下降动量反向传播算法

反向传播算法应用于有样本资料的流域进行洪水预报可以起到很好效果。其主要通过多层网络实现，第一层输入有关资料(如洪水流量或雨量等)，采用有关的学习法则进行训练，输出的结果作为下一层的输入，继续向前传播；将最后一层输出结果与实际结果进行比较，得出误差(一般采用均方误差)；接着运用链式法则和雅可比矩阵推求敏感性，将敏感性从最后一层通过网络逐层被往回传播到第一层；然后采用有关方法更新每一层的权值和偏置值；反复迭代训练，最终使实际输出结果与模型计算的结果之差足够小，其误差最小的模型就是所要建立的模型。

1.1 信息传播过程

反向传播网络(简称BP网络)是一种多层前向的神经网络，其中某一层的输出表示为[11]

am+1=fm+1(wm+1am+bm+1),m=0,1,…,M-1

(1)

式中，w、b、M分别为网络的权值向量、偏置值向量和层数。

第一层从外部接收输入：a0=p。其中，p为输入向量。最后一层输出为整个网络的输出：a=aM。

1.2 性能指数和敏感性

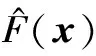
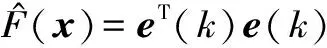
(2)

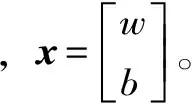
第m层网络输入是该层权值和偏置值的函数

(3)

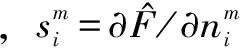
1.3 最速下降动量反向传播法

该算法是最速下降反向传播算法的变形，表示为[11]

Δwm(k)=γΔwm(k-1)-(1-γ)αsm(am-1)T

(4)

Δbm(k)=γΔbm(k-1)-(1-γ)αsm

(5)

式中，α为学习速度；γ为动量系数(0≤γ<1)；Δw、Δb分别为权值和偏置值矩阵的变化量。由于使用了动量项，可以在保证算法稳定前提下提高学习速度，同时可以加速收敛进程。

BP网络不同层的敏感度之间存在如下关系

(6)

式中，n为第m+1层网络输入矩阵。最后一层，即当m=M时

(7)

因此，各层各个元素的敏感度均可以从t与a间的误差通过网络一步一步反向递推至第一层。即

(t-a)→sM→…→s2→s1

(8)

算法过程主要包括：①信息正向传播过程。运用式(1)通过网络将输入向前传播。②误差反向传播过程。运用式(7)和式(6)计算各层各个元素的敏感度、并通过网络将敏感性反向传播，运用式(4)和式(5)更新权值和偏置值。③完成训练和收敛过程。重复以上步骤进行反复训练，直到网络输出的误差小于给定的值ε，或迭代运算达到规定的次数，训练便终止，最终确定的权值和偏置值等参数就可用于模型的模拟。

2 洪水流量预报模型

2.1 流域概况

崇阳溪为闽江上游建溪流域的主要支流，建阳水文站为其主要控制站，位于建阳市城区，站址以上流域面积4 848 km2，其洪水流量主要由崇阳溪、麻阳溪两条支流洪水组合而成，上游设有武夷山水文站、麻沙水文站，集水面积分别为1 078、787 km2(见图1)。建阳水文站多年平均流量188 m3/s，实测最大流量8 380 m3/s(出现时间1998年6月22日)。每年汛期由于北方冷空气南下与西南暖湿气流相遇，往往产生雨区广、雨量多、强度大、历时长的锋面大暴雨，造成洪涝灾害。20世纪80年代以来相继发生了9场大暴雨洪水。

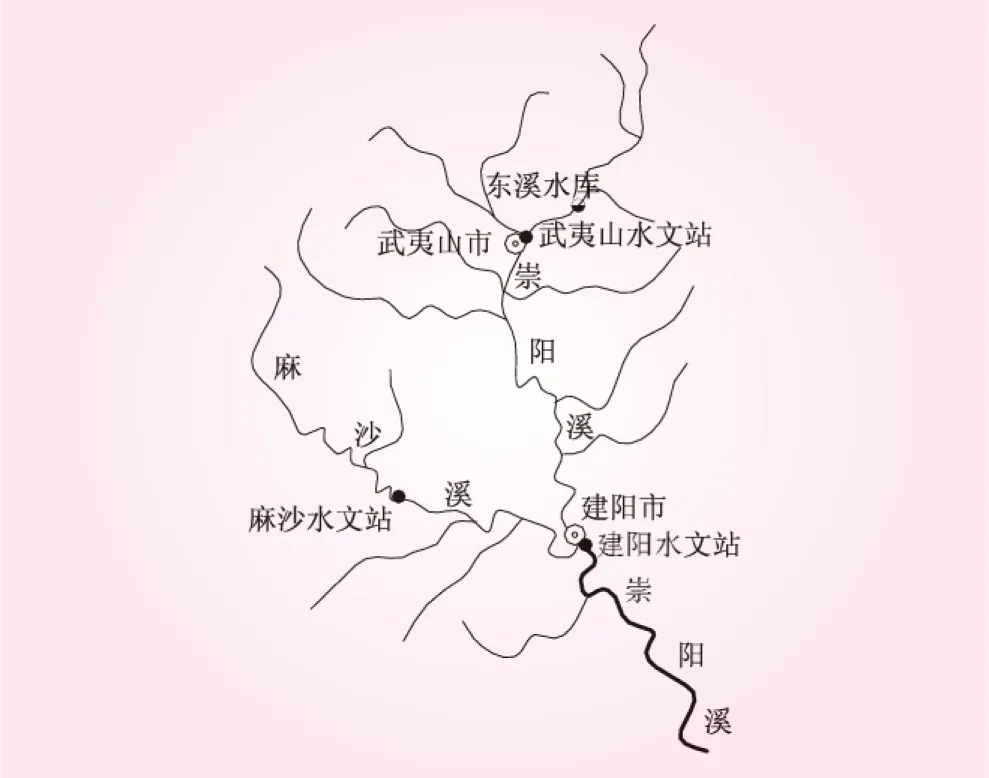
图1 崇阳溪流域水系示意

2.2 模型的构建

崇阳溪干流的洪水流量主要由崇阳溪、麻阳溪两条支流洪水组合而成，相对来讲崇阳溪干流的洪水流量与崇阳溪支流的洪水流量相关系数较大，与麻沙溪支流的洪水流量相关系数较小。由于缺乏支流站点到干流站点的区间入流量资料，此次分析时考虑了建阳站前期流量的自回归影响，以弥补缺乏区间入流可能造成计算结果误差偏大的不足。因此，以上游崇阳溪支流武夷山水文站前τ1小时洪水流量Q1(t-τ1)、麻沙溪支流麻沙水文站前τ2小时洪水流量Q2(t-τ2)、下游崇阳溪干流建阳水文站前T小时洪水流量Q(t-T)作为模型的输入，下游崇阳溪干流建阳水文站相应洪水流量Q(t)为输出，采用最速下降动量反向传播算法建立崇阳溪流域洪水流量预报模型，其中网络的有关参数通过试算优化得出。用简化的河道洪水流量预报模型[12]表示为

Q(t)=f[Q1(t-τ1),Q2(t-τ2),Q(t-T)]+ε(t)

(9)

式中，Q(t)、Q(t-T)分别为建阳站t、t-T时刻的洪水流量，m3/s；Q1(t-τ1)为武夷山站t-τ1时刻的洪水流量，m3/s；Q2(t-τ2)为麻沙站t-τ2时刻的洪水流量，m3/s；τ1、τ2分别为武夷山站、麻沙站至建阳站的洪水传播时间；T为考虑建阳站流量自回归影响的某一时间间隔，一般T>τ1且T>τ2；ε为模型误差；f为从输入空间到输出空间的非线性映射。

依据反向传播算法原理及其在水文水资源应用的有关研究表明：对于一个三层网络，如果在第二层(即隐含层)采用S形传输函数、在第三层(输出层)采用线性传输函数，只要第二层中设置了足够的神经元，就几乎能以任意精度逼近任何非线性映射[13-14]。因此网络采用三层结构(输入层、隐含层和输出层)。输入层包括三个节点：Q1(t-τ1)、Q2(t-τ2)、Q(t-T)；输入层至隐含层函数采用双曲正切S型函数，隐含层至输出层采用线性函数；输出层一个节点Q(t)。

2.3 样本数据处理

选取1959年至2012年间崇阳溪流域建阳水文站及其支流崇阳溪武夷山站、麻沙溪麻沙站42场洪水流量过程资料进行分析。其中，1959年至2002年36场洪水过程资料作为训练样本，2005年至2012年6场洪水过程资料作为检验样本进行验证。

由于不同站点的流量变化幅度不一样，为了取得比较好的收敛效果，常对训练样本中的流量资料进行标准规格化。即分别将三个水文站点的洪水流量数据转变成[-1，1]范围的值

y=2×(Q-Qmin)/(Qmax-Qmin)-1

(10)

式中，Q、Qmax、Qmin分别为训练样本各站的流量值、最大值、最小值；y为标准规格化后的值。

最后对网络输出的结果采用式(11)进行反归一化处理求得建阳站的相应洪水流量

Q=0.5×(y+1)×(Qmax-Qmin)+Qmin

(11)

2.4 模型参数的计算

由于输入层节点、输出层节点以及网络层数均可依据实际情况确定，因此模型结构取决于隐含层节点数。本次采用试错法确定。首先确定隐含层节点数的大致范围，构建不同节点数的反向传播网络，分别进行调试计算，并对所有网络计算结果进行分析比较，从中选取最佳的节点数。本次隐含层节点数分别采用3、4、5、6、7、8、9七种方案进行试算，经对比发现采用6个节点数的方案最优，因此最终确定建阳水文站最速下降动量反向传播洪水流量预报模型采用3- 6-1的结构。此外经过调试，网络的学习速率取0.02，动量系数取0.6，训练90000次后训练样本的平均均方误差为0.0023。最后得到各层间连接的权值及偏置值。

输入层至隐含层权值

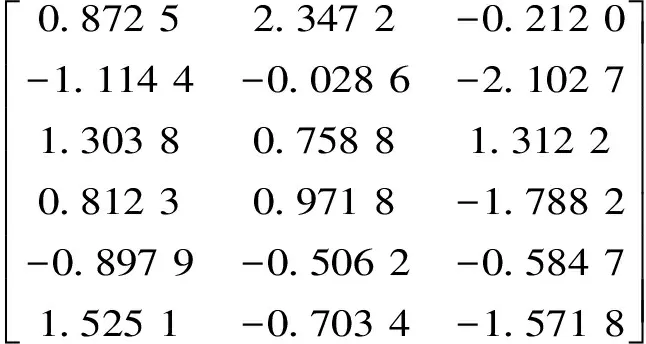
输入层至隐含层偏置值

隐含层至输出层权值[0.058 0 -0.330 3 0.223 8 0.213 2 -0.629 6 -0.669 6]；隐含层至输出层偏置值[0.483 1]。

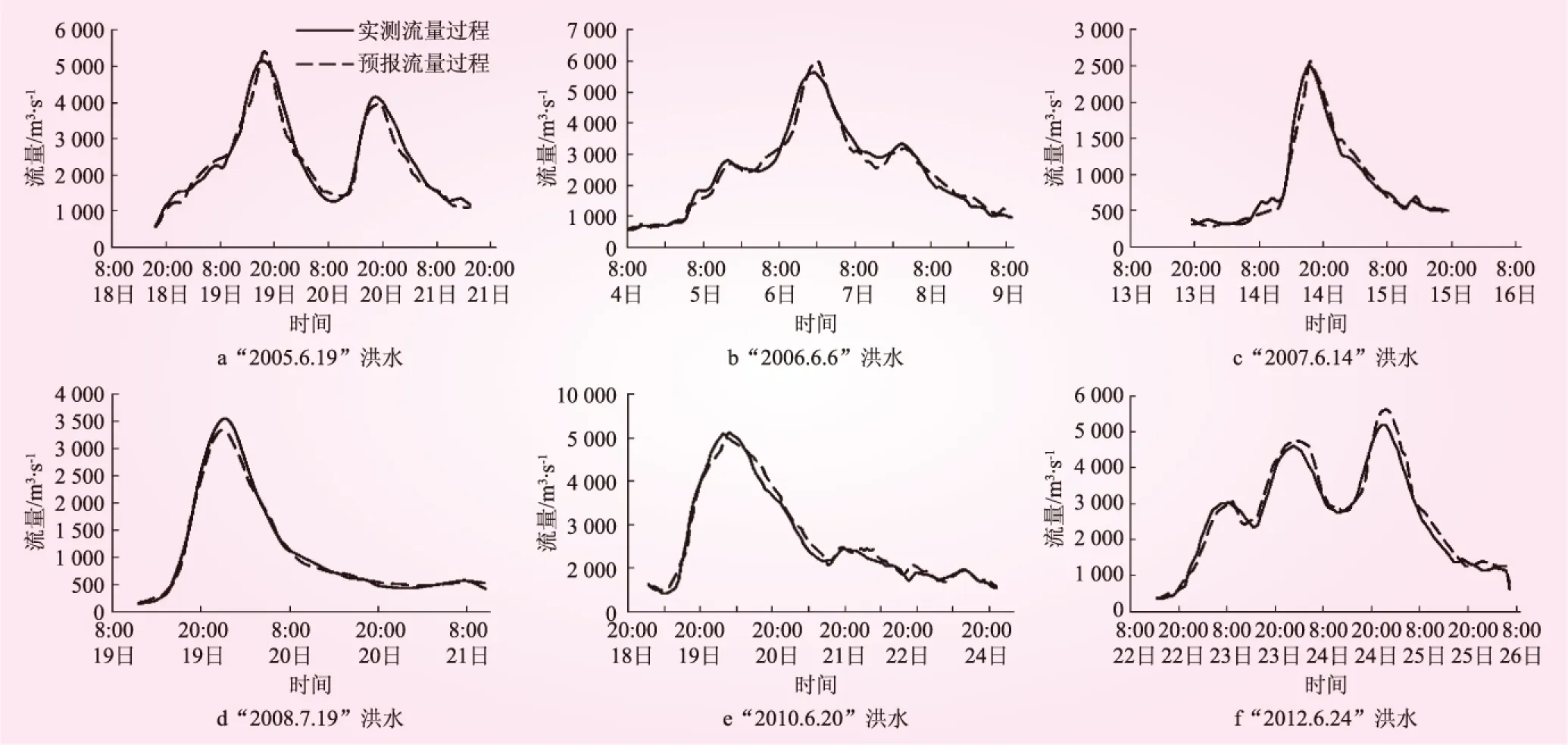
图2 建阳站各场次洪水流量预报过程线

2.5 模型预报结果

采用2005年至2012年的6场洪水资料作为检验样本模拟预测建阳水文站的洪水流量过程，各场次实测和预测洪水流量过程线见图2。

对于每场洪水，采用洪水过程线中所有流量数据点绝对误差绝对值的平均值和相对误差绝对值的平均值、以及模型的确定性系数评价洪水流量预报模型的精度，详见洪水流量预报过程误差统计表1。同时，对每场洪水的洪峰流量预报误差进行统计分析，详见表2。

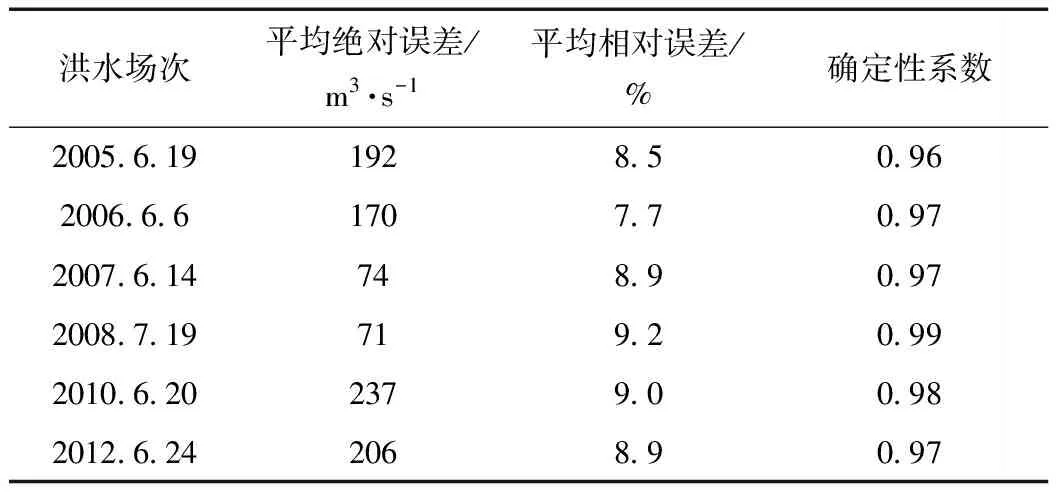
表1 建阳水文站最速下降动量反向传播洪水流量过程预报误差统计

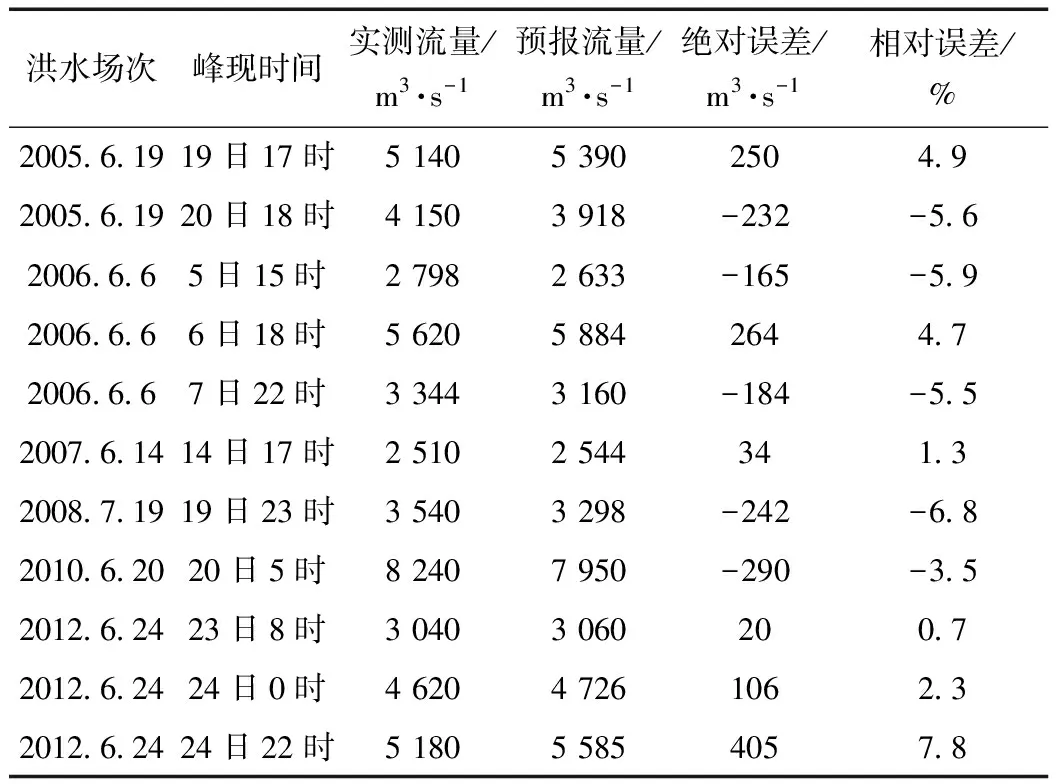
表2 建阳水文站最速下降动量反向传播洪峰流量预报误差统计

从表1可看出，建阳站6场洪水过程预报的平均相对误差在10%以内，确定性系数均在0.9以上；从表2可看出，各次洪峰流量预测值与实测值相对误差也在10%以内，说明模型预测的精度符合要求。

3 结 语

选取系列较长且具有代表性、可靠性和一致性的流量资料，综合分析网络模型的结构，采用试错法确定模型的隐含层节点数，率定和计算模型的相关参数，并加入动量项进行滤波处理，建立了建阳水文站最速下降动量反向传播洪水流量预报模型。应用结果表明，该模型所需求的输入数据为上游有关水文站点的流量资料、下游水文站的前期流量，操作灵活简便，计算速度快，预报准确度较好，是一种比较实用的洪水预报方法。如果能够收集到流域上下游水文站点区间洪水流量资料和雨量资料，代替下游水文站的前期流量，其预报精度和实效性会更好。在实际工作中，可以充分利用流域内洪水预警系统中的测报资料作为输入，采用上述模型进行预报，将预报输出与其他洪水预报方法的结果进行比较，互为验证；然后根据雨情水情的发展，适时修正预报，为流域防洪减灾服务。

[1]范磊, 张运陶, 程正军. 基于MATLAB的改进BP神经网络及其应用[J]. 西华师范大学学报, 2005, 26(1)： 70- 73．

[2]徐敬, 王秀坤, 胡家升. 基于神经网络的无源多传感属性数据关联[J]. 系统仿真学报, 2003, 15(1)： 127- 129．

[3]苏高利, 邓芳萍. 论基于MATLAB语言的BP神经网络的改进算法[J]. 科技通报, 2003, 19(2)： 130- 135．

[4]郭军. BP神经网络算法研究[D]. 武汉： 华中科技大学, 2005．

[5]戴会超, 何文社, 曹叔尤. 基于误差修正的BP神经网络模型在河道洪水预报中的应用[J]. 水电能源科学, 2006, 24(1)： 69- 71．

[6]QING Hualan, YAO Cheng, ZHA Xinima. Test on flood prediction-model using artificial neural network for Shiilian Hydrologic Station on Minchiang, China[J]. Applied Mechanics and Materials, 2011, 39: 555- 561．

[7]陈田庆, 解建仓, 张刚, 等. 基于BP神经网络的马斯京根模型参数动态估计[J]. 水力发电学报, 2012, 31(3)： 32- 38．

[8]胡健伟, 周玉良, 金菊良. BP神经网络洪水预报模型在洪水预报系统中的应用[J]. 水文, 2015, 35(1)： 22- 25．

[9]韩通, 李致家, 刘开磊, 等. 山区小流域洪水预报实时校正研究[J]. 河海大学学报： 自然科学版, 2015(3)： 208- 213．

[10]LIU Wencheng, CHUNG Chuanen. Enhancing the predicting accuracy of the water stage using a physical-based model and an artificial neural network-genetic algorithm in a river system[J]. Water (Switzerland), 2014, 6(6)： 1642- 1661．

[11]HAGAN M T, DEMUTH H B, BEALE M H. 神经网络设计[M]. 戴葵, 等译. 北京： 机械工业出版社, 2002．

[12]金保明. BP神经网络在闽江十里庵流量预测中的应用[J]. 水电能源科学, 2010, 28(9)： 12- 14

[13]MINNS A W, HALL M J. Artificial neural networks as rainfall-runoff models[J]. Hydrological Sciences Journal, 1996, 40(1): 399- 417．

[14]HORNJK K M, STINCHCOMBE M, WHITE H. Multilayer feedforward networks are universal approximators[J]. Neural Networks, 1989, 2(5): 359- 366．

(责任编辑 陈 萍)

Research on Flood Flow Forecast of Chongyang River Watershed Based on Back Propagation Algorithm

JIN Baoming1, LI Yun2, ZHANG Xuan1, GAO Lanlan1, ZHOU Chuanzheng1, FU Xiaolei1
(1. College of Civil Engineering, Fuzhou University, Fuzhou 350116, Fujian, China;2. Hydrology and Water Resources Bureau of Yunnan Province, Kuiming 650106, Yunnan, China)

Based on the principle of Back Propagation algorithm, the number of hidden layer nodes of BP model is determined by trial and error method and the momentum item is added, the steepest descent momentum Back Propagation Neural Network forecast model is established for the flood flow process of Jianyang Hydrological Gauging Station in Chongyang River Watershed. The model uses corresponding flood flow processes of two hydrological gauging stations in the branches of Chongyang River, which are Masha Station in Masha River and Wuyishan Station in Chongyang River, and at the same time, the autoregressive flood flow of Jianyang Hydrological Station is also considered. The results show that the forecast accuracy of model meets application requirements. The forecast model could be used as one of flood flow prediction method and the scientific basis for flood control and flood preparation of watershed．

flood forecasting; flow; Back Propagation algorithm; neural network

2017- 02- 13

福建省自然科学基金资助项目(2016J01734)；河海大学水文水资源与水利工程科学国家重点实验室开放基金面上项目(2015490311)

金保明(1970—)，男，福建浦城人，高级工程师，博士，主要从事水文水资源等方面的研究．

TV124；P338

A

0559- 9342(2017)08- 0022- 04