梯级水电站群联合优化调度函数的逐步回归模型

徐 斌，卢庆文，钟平安，郭 乐，田向忠

(1.河海大学水文水资源学院，江苏南京210098；2.中国长江三峡集团公司，湖北宜昌443133；3.安徽省佛子岭水库管理处，安徽六安237272)

梯级水电站群联合优化调度函数的逐步回归模型

徐 斌1，卢庆文1，钟平安1，郭 乐2，田向忠3

(1.河海大学水文水资源学院，江苏南京210098；2.中国长江三峡集团公司，湖北宜昌443133；3.安徽省佛子岭水库管理处，安徽六安237272)

针对梯级水电站群联合优化调度函数识别中存在的线型选择及变量筛选问题，采用逐步回归模型筛选关键作用变量并建立回归调度函数方程，以保证调度函数的简洁、有效性。将模型应用于金沙江与三峡四库梯级系统提取消落期系统联合优化调度函数，从四库梯级联合优化调度样本中通过逐步回归调度函数辨识溪洛渡、三峡水库协同消落机制并检验了模型精度。结果表明：在率定来水样本条件下，逐步回归调度函数拟合误差均在3%以内，拟合精度较高；在检验来水样本条件下，与多元线性回归调度函数相比，逐步回归调度函数对应总发电效益平均增加1.67亿元(0.69%)。由于逐步回归调度函数剔除了次要因素干扰，相较于多元线性回归调度函数泛化能力更优，具有更高实用价值。

梯级水电站群；水库优化调度；调度函数；逐步回归

0 引 言

水库优化调度技术利用优化理论指导水库实际调度，具有显著经济效益[1-2]。在水库中长期调度中，受限于预报技术条件以及信息采集条件，降雨、径流等关键信息的预测结果仍具有高度不确定性，导致水库调度成为不完全信息条件下的序贯决策问题。不完全信息下水库调度决策问题有显式随机优化方法和隐随机优化方法[3- 4]两类解决办法。显式随机优化方法将径流过程假定为已知分布的随机过程并离散化，然后寻求统计意义最优的调度策略，该法的关键在于确定径流的随机描述方式及离散方法[5]，当离散场景数过多时由于计算规模庞大导致“维数灾”问题。隐随机优化方法[5]先生成若干径流样本序列，然后对于每一组径流样本采用确定型优化模型求解相应的最优调度策略，再从大量径流、决策样本中提取相应的调度函数关系。调度函数以仅考虑面临时刻及以前的已知信息或状态变量为自变量，规避了使用具有高度不确定性的预报信息，该方法关键在于选定合适的自变量以及函数形式。相对于显式随机优化方法[7]，调度函数更为直观有效[8]。

截至目前，关于调度函数线型构造及自变量选取已有大量研究成果。其中，线型构造可分为显函数与隐函数两种。显式调度函数中以多元线性函数构型研究最多，如周研来[9]等、刘攀[10]等以多元回归分析分别建立大渡河梯级水库群、清江梯级水库群联合优化调度函数，并验证了调度函数有效性；许银山[11]等采用聚合分解的思想将大规模水库水电站群进行等效聚合并求解相应优化模型，然后采用逐步回归模型识别水库群调度规则。隐函数中以神经网络模型最具代表性，如缪益平[12]等建立神经网络模型模拟凤滩电站调度函数并比较了与常规回归方法的差异，刘宇[13]等针对神经网络应用于调度规则提取时的隐层节点参数率定问题展开研究。然而，神经网络模型参数众多、结构复杂，往往存在自由参数过多而导致模型拟合精度高但泛化能力差的“过拟合”问题。同样，线性调度函数的自变量选择也存在类似问题，大量干扰变量的引入将导致模型泛化能力降低。因此，因子(自变量)筛选对于提高模型辨识能力至关重要。

本文运用逐步回归理论从备选因子集中筛选对决策变量起显著作用的主要影响因子及其阶次，然后建立逐步回归模型提取梯级水库群联合优化调度函数。通过应用于金沙江下游至三峡四库梯级水电站群系统，以系统消落期联合优化调度结果为样本，验证了逐步回归调度函数拟合精度及泛化性能的优越性。

1 水库群联合优化调度函数

水库群联合优化调度函数，即水库群联合优化调度决策变量与已知变量的关系函数。相较于水库群联合优化调度模型，调度函数能更直观反映最优决策与主要影响变量的相互关系，进而揭示联合调度机理。一般而言，水库群联合调度函数可表述为如下结构

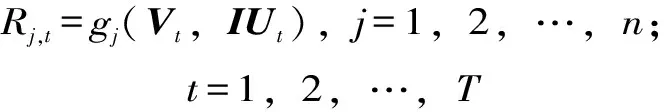
(1)

式中，Vt=[V1，t，V2，t，…，Vn，t]T、IUt=[Iu1，t，Iu2，t，…，Iun，t]T分别为系统各库在时段t的蓄量、区间入流向量，其中，Vj，t为j库t时段初蓄水量，m3；IUj，t为j库t时段平均区间入流(第一级水库即入库流量)；gj(·)即各库相应函数映射关系。

式(1)表明，由于水库群联合补偿机制作用，各库放水决策变量不仅取决于本库蓄量状态以及区间来水量，且与其余库相应时段状态变量及区间来水量有关。此外，自变量对决策变量贡献关系可能因补偿机制的差异而各异，即多项自变量间存在主次关系。次要变量的引入可能因为变量之间相关关系造成信息冗余或信息干扰，影响决策者对关键作用机制的辨识。因此，如何遴选关键作用变量以凸出调度函数直接作用机制对于提高调度函数辨识度和泛化能力具有关键作用。以水库群联合优化调度模型[9]求解所得优化调度样本为输入，本文采用逐步回归理论进行关键因子筛选以及调度函数拟合。

2 逐步回归理论

逐步回归理论采用自变量对因变量的方差贡献作为指标筛选自变量集中的显著变量。通过逐个引入显著变量、剔除次要变量直至模型中仅包含对因变量有显著影响的变量为止。

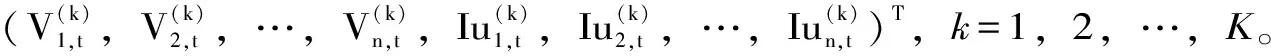
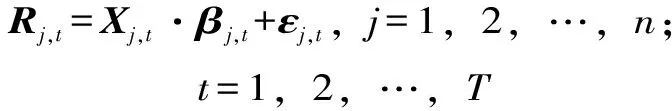
(2)

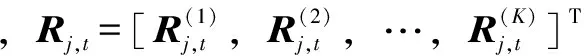
逐步回归模型即从式(2)中优选对决策变量具有显著影响的因子进行回归分析。每一步只挑选一个因子，则逐步回归进行到第l步的基本步骤如下：

(1)分别对2n个因子计算其方差贡献(偏回归平方和)以衡量自变量各因子重要性。

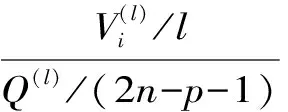
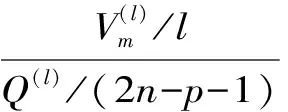
(4)引入以及剔除因子后，令l←l+1，利用矩阵变换法计算l步的回归系数，转步骤(2)。重复进行直至方程中既不能引入也不能剔除因子为止。

通过逐步回归分析，得到的方程中只包含对决策变量有显著影响的因子。利用复相关系数评价逐步回归模型的水库联合调度规则函数拟合精度。

3 算例分析

以金沙江下游至三峡四库即溪洛渡、向家坝、三峡和葛洲坝梯级为例进行研究。该四库梯级巨型综合水利枢纽兼有防洪、发电、拦沙、改善航运条件、保障环境和经济社会供水等多个目标。其中，发电是四库调度目标中主要效益指标之一：金沙江四库梯级总装机容量约6 500万kW，是我国西电东送工程体系中重要组成部分。枢纽由中国三峡集团公司梯级调度中心统一调度，研究该梯级枢纽联合优化调度规则对于指导梯级实时调度、提高调度效益具有重要实践意义与经济价值。

以逐步回归模型辨识梯级四库消落期(12月至次年6月)调度规则。针对四库实际运行限制以及各库调节性能、开发功能和水力联系等条件，构造联合优化调度样本计算条件如下：

(1)消落期末(6月底)各库均控制消落至汛限水位。此外，考虑消落期初不同水库蓄水状态，设置溪洛渡、三峡不同组初始库容条件。

(2)将1940年～2013年共74年逐月长系列实测径流资料排频分为丰水年组、平水年组和枯水年组3种来水系列，从各年组中各挑选一代表年作为验证来水系列，以除去典型三年的71年来水系列作为率定系列，输入联合优化调度模型并生成联合优化调度样本。

3.1 三峡四库梯级消落期联合调度函数

采用逐步回归模型对联合优化调度样本逐月进行调度规则拟合。因葛洲坝水库调节性能低，对于月径流过程调节无需调度规则。不同时段联合优化调度函数及对应控制规则如下：

(1)消落期初(12月～次年2月)溪洛渡、向家坝发电流量仅与溪洛渡当月入库有关，两库对应12月调度函数为R1，1=IU1，1-0.68、R2，1=1.01IU1，1-0.69；1月调度函数为R1，2=0.72IU1，2+531、R2，2=0.73IU1，2+531；2月调度函数为R1，3=0.56IU1，3-0.22V1，3+3351、R2，3=0.57IU1，3-0.22V1，3+3352；

(2)3月、4月溪洛渡放水依溪洛渡入流呈分段线性特征：当溪洛渡入库不足最小下泄流量要求，则按最小下泄流量控制；否则，溪洛渡放水需兼顾三峡水库蓄量与三峡区间入流大小实施适量补偿。同期，三峡发电流量主要受最小下泄流量(6 000 m3/s)约束限制。具体函数规则如下：3月溪洛渡、三峡调度函数分别为

R3，4=6 000；

R3，5=6 000。

(3)消落期末(5月、6月)溪洛渡放水与其当前可用水量(V1，t+IU1，t·Δt)呈正比；同期三峡放水同时与溪洛渡当前可用水量(V1，t+IU1，t·Δt)及三峡当前可用水量(V3，t+IU3，t·Δt)正向关联。即5月～6月三峡、溪洛渡呈协同消落[13]状态。

以6月份调度函数及联合优化调度样本数据为例，溪洛渡、三峡调度函数平面与联合优化调度样本拟合关系如图1所示。

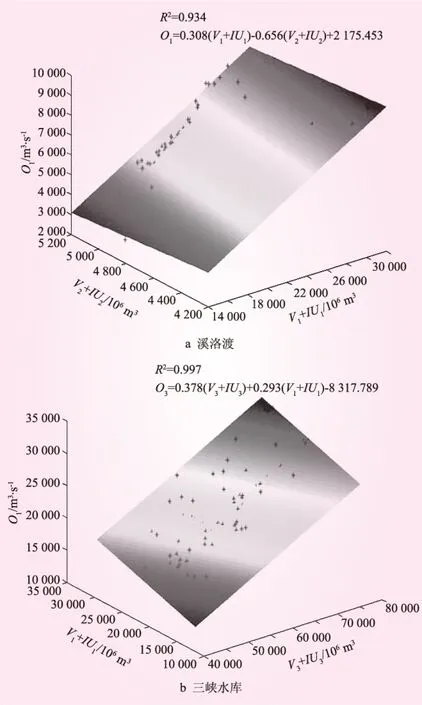
图1 溪洛渡、三峡水库联合优化调度函数与联合优化调度样本

从图1可见：采用逐步回归调度函数计算的出库流量数据与联合优化调度样本的相对误差较低，且绝大部分点据均匀分布在调度函数曲面附近。逐步回归调度函数与样本拟合度高。

3.2 调度函数泛化能力校验

逐时段拟合的联合优化调度函数所得发电流量与原联合优化调度样本中的发电流量存在拟合误差。由水量平衡方程及梯级水电站群的水力联系可知，在应用于指导实时调度时发电水量误差将逐时段传递并影响下游水库入库水量。因此，调度函数的拟合误差将造成实时调度策略与理论最优调度策略偏离，导致调度函数调度策略对应的系统效益低于理论最优调度策略所得系统效益。

可见，采用拟合精度指标无法评估调度函数在应用于指导实际调度过程中的有效性。针对上述问题，本文分别以逐步回归调度函数、线性回归调度函数作为调度指导规则，以验证来水系列中丰、平、枯三种典型年来水条件下，采用两种调度函数的调度方案与联合优化调度样本调度方案蓄量的差异，检验、比较调度函数泛化能力[5]。

图2、3分别为丰水年、枯水年下溪洛渡、三峡两库在两种调度函数下调度过程与联合优化调度蓄量过程对比图。由结果可知，两种调度函数对应调度策略均不同程度偏离联合优化调度样本调度方案过程，由于剔除干扰因子影响，逐步回归调度策略距联合优化调度策略偏离程度更小，泛化能力更强。其中，在消落期末(5月、6月)调度函数调度策略与联合优化调度策略偏离程度最高，反映拟合误差的累积效应影响。

对联合优化调度、逐步回归调度函数以及多元线性回归调度函数对应三种调度策略在不同来水典型年下的调度效益结果进行比较，具体见表1。

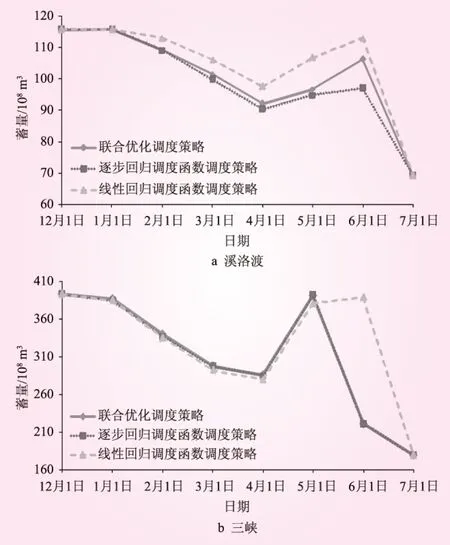
图2 丰水年水库调度蓄量过程对比

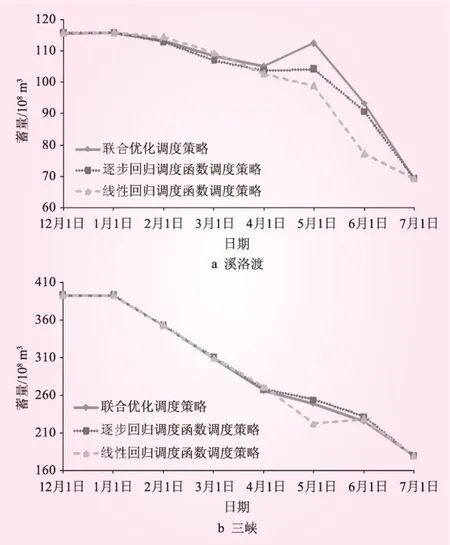
图3 枯水年水库调度蓄量过程对比

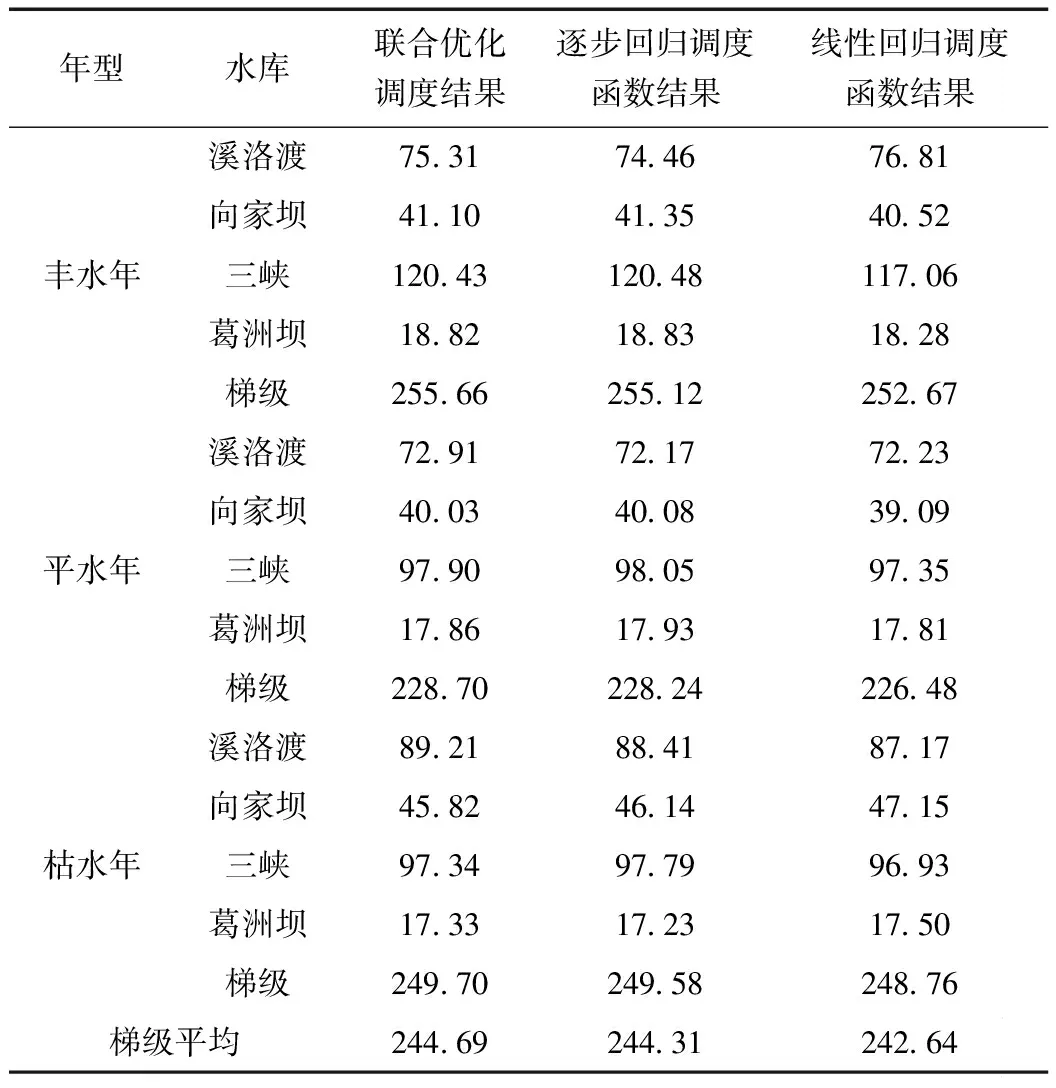
表1 不同调度模式下梯级四库调度发电效益 亿元

从表1可以看出：

(1)较联合优化调度结果，逐步回归调度函数对应系统总发电效益在丰、平、枯水年型下效益分别降低0.54亿(0.21%)、0.47亿(0.2%)、0.12亿元(0.05%)，平均降低0.38亿元(0.15%)。结合图2a和图3a可知，逐步回归调度函数计算得溪洛渡出库流量结果偏高，使消落期2月～5月期间水位过程低于同期联合优化调度水位过程，进而导致溪洛渡水库水头效益受损。在三种年型下，相较于联合优化调度结果，逐步回归调度函数调度结果中对应溪洛渡效益损失分别为0.85亿、0.74亿、0.8亿元，是导致梯级总发电效益降低的主要原因。

(2)与线性回归调度函数调度结果相比，逐步回归调度函数对应系统总发电效益在丰、平、枯水年型下效益分别增加2.45亿(0.96%)、1.75亿(0.77%)、0.82亿元(0.33%)，平均增加1.67亿元(0.69%)。效益增加机制因年型而异，丰水年型下，因为逐步回归调度函数调度策略在5月底加快对三峡水库的消落，减少了6月份三峡、葛洲坝弃水进而增加了对应库发电水量，使三峡、葛洲坝分别增加效益3.42亿、0.55亿元；枯水年型，由于抬高溪洛渡、三峡运行水位分别使两库增发不蓄电能，效益增益分别为1.23亿、0.86亿元。

由此可见，由于逐步回归调度函数剔除次要因素对调度规则的干扰，能更准确地反映库群联合调度机制，综合效益高于多元回归调度函数对应结果。

4 结 论

本文采用逐步回归模型提取水库群联合优化调度函数，通过因子筛选、剔除与因变量关系不显著的干扰因子，使调度函数直观揭示联合优化调度机制。以金沙江与三峡四库梯级消落期联合优化调度结果为样本，通过逐步回归模型识别各库消落期逐月调度函数，并验证调度函数拟合效果以及泛化能力。结果表明，相较于联合优化调度样本，在典型来水条件下，逐步回归调度函数对应系统总发电效益平均降低0.38亿元(0.15%)；与线性回归调度函数调度结果相比，逐步回归调度函数对应系统总发电效益平均增加1.67亿元(0.69%)。

[1]钟平安, 徐斌, 张金花. 水电站发电优化调度遗传算法的改进[J]. 水力发电学报, 2011(5): 55- 60．

[2]赵铜铁钢. 考虑水文预报不确定性的水库优化调度研究[D]. 北京: 清华大学, 2013．

[3]LEE J, LABADIE J W. Stochastic optimization of multireservoir systems via reinforcement learning[J]. Water Resources Research, 2007, 43(11): 59- 68．

[4]LABADIE J W. Optimal operation of multireservoir systems: state-of-the-art review[J]. Journal of Water Resources Planning and Management. 2004, 130(2): 93- 111．

[5]XU B, ZHONG P, ZAMBON R C, et al. Scenario tree reduction in stochastic programming with recourse for hydropower operations[J]. Water Resources Research. 2015, 51(8): 6359- 6380．

[6]陈洋波. 水电站水库隐性随机优化调度研究[J]. 水利学报, 1998(2): 27- 30．

[7]CELESTE A B, BILLIB M. Evaluation of stochastic reservoir operation optimization models[J]. Advances in Water Resources. 2009, 32(9): 1429- 1443．

[8]姜瑾, 张永永.基于改进调度函数的梯级水库群联合调度研究[J]. 水力发电, 2013, 39(9)： 76- 79.

[9]周研来, 梅亚东, 杨立峰, 等. 大渡河梯级水库群联合优化调度函数研究[J]. 水力发电学报, 2012(4): 78- 82．

[10]刘攀, 郭生练, 张文选, 等. 梯级水库群联合优化调度函数研究[J]. 水科学进展, 2007(6): 816- 822．

[11]纪昌明, 苏学灵, 周婷, 等. 梯级水电站群调度函数的模型与评价[J]. 电力系统自动化, 2010(3): 33- 37．

[12]缪益平, 纪昌明. 运用改进神经网络算法建立水库调度函数[J]. 武汉大学学报： 工学版, 2003(1): 42- 44．

[13]刘宇, 钟平安, 张梦然, 等. 隐层节点数经验公式在水库调度规则提取中的应用效果评价[J]. 水电能源科学, 2012(11): 42- 44．

[14]符芳明, 钟平安, 徐斌, 等. 金沙江下游与三峡梯级水库群协同消落方式研究[J]. 南水北调与水利科技, 2016(4): 29- 35．

(责任编辑 焦雪梅)

Stepwise Regression Model for Extracting Joint Optimal Operation Rules of Cascade Hydropower Stations

XU Bin1, LU Qingwen1, ZHONG Ping′an1, GUO Le2, TIAN Xiangzhong3
(1. College of Hydrology and Water Resource, Hohai University, Nanjing 210098, Jiangsu, China;2. China Three Gorges Corporation, Yichang 443133, Hubei, China;3. Foziling Reservoir Management Office, Anhui Province, Liuan 237272, Anhui, China)

To solve the problems of curve type selection and variables selection existing in the recognition of optimal operation rules for cascade hydropower stations, the stepwise regression model is introduced to filter key variables and establish regression operation function equation. The model is applied to extract the joint optimal operation rules of downstream Jinsha River and Three Gorges Cascade reservoirs system during drawdown season, and the joint operation mechanism between Xiluodu and Three Gorges reservoirs is identified by the model with the input data samples from the joint optimal operation policies. The accuracy of model is also tested. The results show that: (a) the calibration errors of rules are less than 3% compared with the calibrating data samples, so the calibration precision is higher; and (b) comparing with the multiple linear regression rules without variables selection, the total benefit of power generation obtained by the stepwise regression rules will increase 167 million Yuan (0.69%) in average under the test samples. Since the stepwise regression rules can eliminate the influences of insignificant factors, it has better forecasting ability than the multiple linear regression rules and is more effective in guiding reservoir operation．

cascade hydropower station; reservoir optimal operation; operation rule; stepwise regression

2016- 11- 30

国家自然科学基金项目(51609062、51579068)；国家重点研发计划项目(2016YFC0400909)；中央高校基本科研业务费专项资金资助项目(2015B28414)

徐斌(1986—)，男，湖南长沙人，讲师，博士，主要从事水资源规划与管理研究．

TV697

A

0559- 9342(2017)08- 0099- 05