基于服务损失函数的集装箱码头泊位—岸桥联合调度优化
王智灵,刘桂云,刘明涛
(宁波大学海运学院,宁波 315211)
发展战略与项目管理
基于服务损失函数的集装箱码头泊位—岸桥联合调度优化
王智灵,刘桂云*,刘明涛
(宁波大学海运学院,宁波 315211)
面对不确定环境、多样性和差异化服务需求,集装箱码头亟需改进和优化调度方法,提高码头作业效率和客户满意度。针对集装箱码头泊位与岸桥的资源分配问题,通过添加缓冲时间来吸收不确定因素对调度计划产生的影响,引入多元服务质量损失函数建立以偏离最优靠泊位置、岸桥移动损失及在港时间损失为目标的优化模型,利用改进的遗传算法对模型进行求解,并通过试验算例证明了模型及算法的有效性。
不确定环境;服务损失;泊位与岸桥;客户满意度;遗传算法
集装箱港口间的竞争日益激烈,要在竞争中取得优势,必须使港口的物流作业系统化、合理化,为船舶的装卸提供一个良好的物流作业平台,最有效途径是优化港口资源的分配与调度。泊位和岸桥是集装箱码头稀缺与瓶颈资源,其协同作业效能决定了码头的整体作业能力。因此,合理的安排泊位与岸桥,制定有效的作业调度计划能够提高集装箱码头的作业效率和服务质量,增加客户满意度,同时降低码头的运营成本,提升竞争力。
集装箱码头运作过程中存在许多不确定因素与难以预料的突发事件,使得作业不能正常运作,例如船舶到港时间的变动、岸桥操作时间的不确定等因素。因此不确定环境下的泊位与岸桥联合调度问题的研究更加接近实际情况。Lu[1]等针对连续、动态不确定性泊位的调度问题,设计了前馈调度方案并改进反馈方案,利用启发式算法进行了求解。陈秋双等[2]针对不确定环境下集装箱码头的扰动管理问题对作业过程中的不确定因素分类,运用随机变量、模糊集等进行数学描述,阐述鲁棒调度模型的建立和求解技术。Han等[3]考虑船舶到港时间的不确定性,建立了离散型的泊位与岸桥联合调度模型,通过遗传算法和抽样仿真求解得出鲁棒性的调度计划。杨春霞[4]针对固定靠泊和柔性靠泊两种靠泊方式,以最小化船舶在港时间和码头生产成本为目标,设计了一种基于可变调度深度改进型的混合重调度策略。孙彬等[5]提出一种在不确定环境下基于鲁棒反应式策略的离散型泊位和岸桥调度方法,设计了一种基于CNP协商机制的岸桥实时调度模型,提高系统的抗干扰能力。桂小娅[6]考虑船舶到达时间的不确定性,建立了确定条件和不确定性条件下的前摄-反映两阶段调度模型,运用双层循环迭代算法进行求解。粱承姬等[7]针对船舶到港时间和装卸作业时间随机问题,建立了以船舶在港总时间、偏离偏好泊位的惩罚时间及延缓时间之和最小为目标的混合整数规划模型,提出一种启发式靠泊的改进遗传算法进行求解。
企业在生产、经营过程中,产品的质量问题给企业带来大量的损失,目前关于质量损失的研究集中在加工制造业中零件质量的有形损失。艾延廷等[8]针对轴承组建装配问题,以装配质量损失最小为目标,建立了基于信噪比的多元装配质量损失模型,采用遗传算法进行求解。匡芬[9]等基于质量损失函数构建了加工过程的产品特性与任务载荷要求、过程特性与生产能力的关系模型,定量评估加工过程中各种随机因素对可靠性的影响。Yadav等[10]综合考虑了质量损失问题、全寿命周期等问题,构建多目标优化的复杂质量损失函数模型。彭和平等[11]将多重相关质量损失函数应用于公差设计中以降低生产成本。
按照Aytug[12]中的分类,现有的不确定性调度方式包括完全反应调度、前馈—反馈调度和鲁棒性调度。完全反应调度在计划中不考虑随机性,随着执行过程采用调派规则进行实时调度。前馈—反馈调度是指在已有调度方案基础上,当不确定性发生时,对方案进行调整的方式。鲁棒性调度在制定计划时考虑不确定性,以求最小化主要不确定因素对实际运行结果带来的影响。在鲁棒性调度中,通过添加缓冲时间来吸收不确定性的方法运用十分广泛,但对于在不确定条件下的泊位与岸桥联合调度问题,通过添加缓冲时间方式的鲁棒性调度研究很少。
在码头作业中,最常见的两种不确定因素是船舶到达时间和岸桥的操作时间。因此本文从这两种不确定因素出发,通过添加缓冲时间吸收不确定因素,建立基于客户满意度的不确定环境下泊位与岸桥联合调度模型,增强调度方案的鲁棒性。引入多元服务质量损失函数作为目标函数来度量码头服务质量的损失,具体的服务损失包括船舶在港时间的损失、偏离最佳靠泊位置的损失以及岸桥移动损失,建立在保障船舶总体满意度条件下,码头服务损失最小的调度模型并采用改进的遗传算法进行求解,使调度结果更优。
1 多元服务质量损失函数
在衡量客户满意度水平时,引入田口质量损失函数。田口玄一[13]将质量损失定义为产品产出后对社会的损失,包括直接损失和间接损失。质量特性值偏离目标值越大,造成的损失就越大。为了定量描述产品质量损失,田口提出了“质量损失函数”的概念,并以信噪比来衡量设计参数的稳健程度。田口质量损失函数用一个二次损失函数来估计当产品质量特性值偏离目标值时的产品质量损失。令L(Y)为由质量指标Y偏离目标值而引起的经济损失,m为顾客目标值。若L(Y)在Y=m存在二阶导数,则L(Y)在Y=m附近按泰勒级数展开,可以近似地表示为

式中:Y=m时损失最小且为零,即L(m) = L′(m) = 0,损失函数可以表示为

式中:K为质量损失系数,其中K = L"(m)/2!,不依赖Y的常数。
由于二次质量损失函数式(2)中的质量损失系数K是由服务质量特性所造成的经济损失所决定,然而确定该经济损失是非常困难的,田口选择一个使质量损失函数对所采用的单位不敏感的质量损失系数,令并提出了无量纲的标准化质量损失函数

式中:TU、TL分别为产品质量特征的公差上下限。
标准化的质量损失函数是无量纲,所以质量损失函数可以相加求和。集装箱码头客户服务损失具有田口损失函数的特性,故多元服务质量损失函数可表示为

2 问题描述
在集装箱码头的实际运作中,多种不确定因素会影响船舶泊位与岸桥调度,主要表现在船舶到达时间和岸桥装卸作业的不确定性等。针对不同特点的不确定性的描述,最常用的方法有两种:一种是不确定性参数服从概率分布,即通过分析运营数据统计出参数所服从的概率分布,通常情况下采用随机变量描述调度系统的不确定性,如各作业任务执行时间的不确定性和任务到达时间的不确定性。另一种是不确定性参数处于某一区间,即通过统计分析运营数据,整理出参数所处的某个区间,用区间表示参数的不确定性。本文综合这两种方法处理泊位与岸桥调度中的不确定性。假设船舶的实际到港时间服从以计划到港时间为均值的均匀分布,即为船舶到港时间的变动范围。同时,装卸作业时间Bi也是服从岸桥平均作业时间为均值的均匀分布。
为了增加调度计划的鲁棒性,通过添加缓冲时间的方法吸收不确定性因素带来的影响,根据船舶到港时间的变动范围来确定缓冲时间的最大值,即φmax= 2α,α为船舶到港时间的标准差,由船舶到港时间的变动范围ΔCi得出。φ存在两种情况,φ > 0表示船舶延迟到港,即实际到港时间在[Ci,Ci+ΔCi]范围内,则给船舶添加的缓冲时间为正数,φ < 0表示船舶提前到港,即实际到港时间在期望到港时间范围内,则添加的缓冲时间为负数。如果缓冲时间添加的足够大,那么能够吸收的不确定性也就比较大,计划的鲁棒性就更强,调度计划的鲁棒性可以用缓冲时间的大小来体现,因此在目标函数中加入了最大化缓冲时间。
考虑动态、连续泊位下的调度问题,泊位是连续岸线,能够有效利用泊位资源。引入靠泊损失,如果偏离最优靠泊位置就会增加作业成本。引入岸桥移动损失,岸桥可在船舶间进行移动装卸,提高装卸利用率,但频繁的移动会增加过多岸桥移动成本。客户的满意度用在港时间损失来衡量,即所有在港船舶在期望时间内离港,损失越小,客户的满意度越高。
3 调度模型
3.1 模型假设
为了更好的建立模型,根据问题的特性和现实约束,提出以下假设:
(1)连续泊位各处均符合船舶靠泊的水深条件;(2)船舶到港后才进行靠泊服务,船舶靠泊和离港操作时间不计;(3)遵循一次靠泊原则且每艘船舶都有自己的最优靠泊位置;(4)岸桥均位于同一轨道上,从左至右依次编号;(5)岸桥移动不能交叉跨越,两台岸桥之间存在安全距离;(6)岸桥的移动时间忽略不计;(7)某一时刻,岸线上所有船舶的贝位从左至右依次编号;(8)每艘船舶都有最小和最大岸桥数的限制。
3.2 符号定义
3.2.1 集合与参数
V={1,...,n},计划期到港船舶集合,用i和j代表不同的船舶编号;Q={1,...,q},码头可用岸桥集合,q为岸桥号,k为岸桥数;T={1,...,t}计划期时间段集合,t为时间段号;Ωi为船舶i的任务量,i∈V;L为码头岸线总长度;li为船舶i的长度,包括前后的安全距离,i∈V;pbi为船舶i的最优靠泊位置,i∈V;Ci为船舶i的计划到港时间,i∈V;Ai为船舶i的实际到港时间,服从以计划到港时间为均值的均匀分布,i∈V;Bi为船舶i单个岸桥的处理时间,服从以平均处理时间为均值的均匀分布,i∈V;Di为船舶i的期望离港时间,i∈V;rimin和rimax为船舶i所需最小和最大岸桥数,i∈V;v为单个岸桥单位时间的作业效率;λ1,λ2,λ3分别为在港时间损失、偏离最优靠泊位置损失、岸桥移动损失的权重。
3.2.2 决策变量
bi为船舶i靠泊位置;bli为船舶i向左偏离最优靠泊位置的偏离差;bri为船舶i向右偏离最优靠泊位置的偏离差;Si为船舶i的开始服务时间;ei为船舶i结束服务的离港时间;xij∈(0,1),若船舶i在空间上完全停靠在船舶j之前则为1,否则为0;Qit为t时刻分配给船舶i的岸桥数量;yitq∈(0,1),若船舶i在t时间内被岸桥q服务则为1,否则为0;changeit为船舶i在t时刻相对于t-1时刻岸桥数目增加的数量;ji为船舶i的延缓时间;σ∈(0,1),若船舶i有k个岸桥服务且延缓时间为t则为1,否则为0;busyit:判断船舶i在t时刻是否处于作业状态;di∈(0,1),若船舶i的离港时间大于期望离港时间则为1,否则为0。
3.3 目标函数
建立如下基于服务损失函数的调度模型,其目标函数为
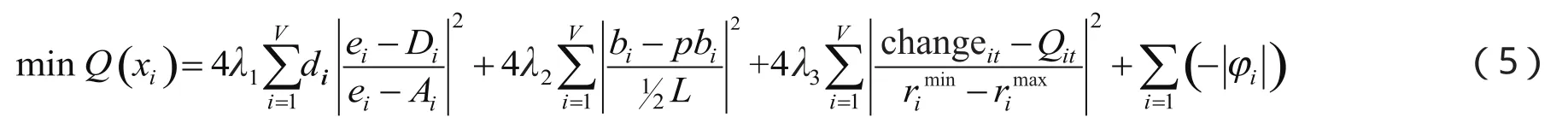
目标函数(5)第一部分,表示顾客的在港时间服务损失,期望离港时间、实际到港时间为船舶在港时间服务质量特征偏差的上下限;第二部分,表示船舶偏离最优靠泊位置的服务损失,考虑到是连续泊位取1/2岸线长度作为靠泊服务质量特征的偏差;第三部分,岸桥的移动损失,每艘船的装卸岸桥有最大最小数量限制,可作为岸桥移动服务质量特征偏差的上下限;第四部分表示添加的延缓时间的绝对值最大。
3.4 约束条件
式(6)边界约束,所有船舶都必须靠泊在码头岸线范围内

式(7)和式(8)确保没有两艘船舶在同一地点同一时刻被服务

式(9)表示船舶到港后才能进行作业

式(10)确保所有船舶的任务量都能得到满足

式(11)表示任意时间段内分配给所有船舶的总数满足码头可用岸桥总数

式(12)表示岸桥只有满足此要求才可开始作业

式(13)定义每艘船任务处理时间

式(14)表示每一岸桥在同一时刻只能为一艘船舶服务

式(15)表示某时刻服务于同一船舶的岸桥数量

式(16)限制分配给同一船舶的岸桥是连续的且不能跨越

式(17)表示船舶在任意时间段内分配到的岸桥数目必须符合码头剩余可用岸桥数量的限制

式(18)定义某一时刻到下一时刻岸桥数量的增加数量

式(19)保证以岸桥作业结束时间为船舶的实际离港时间

式(20)表示延缓时间内船舶的岸桥数不变

式(21)保证船舶任务量能够满足且延缓时间内该船舶还占用泊位和岸桥资源

式(22)和(23)定义决策变量

式(24)定义0-1变量

4 算法求解
4.1 个体编码设计
采用自然数编码方式,染色体的每一列代表服务船舶的相关信息,染色体编码如表1所示。以第二排为例,船舶2的停靠位置为350,分配的岸桥数量为3,添加的缓冲时间为0。
4.2 种群初始化
根据集装箱船舶的到港总数V,采用随机生成1到V间的随机整数。对于连续泊位的问题,泊位是一条连续的岸线,因此设定船舶在岸线上靠泊的位置为船舶的最左端。船舶靠泊位置部分的染色体在[0,L]范围内随机产生。根据各船舶所需的岸桥数目的需求,分配的岸桥数量即岸桥部分的染色体在[rimin,rimax]之间随机产生。添加的缓冲时间部分的染色体虽然也是随机产生,但是受到船舶实际到港时间的约束。船舶实际到港时间服从以计划到港时间为均值的均匀分布,即船舶在[Ci-ΔCi, Ci+ΔCi]时间段内随机到达,船舶有可能提前或者延迟到港。因此缓冲部分染色体的生成步骤为:判断船舶i的到港时间Ai与计划到港时间Ci的关系,若Ai≥Ci,则在[0, φi]随机产生;若Ai≤Ci,则在[-φi,0]随机产生。
4.3 适应度函数
根据目标函数是最小化问题,采用如下公式计算种群中的个体适应度值

式中:c为大于0的数。由于目标函数始终为正值,所以取c=0。通过这个适应度函数可以看出服务损失Q(xi)越小,适应度值f(xi)越大,在选择操作中被选中的概率就越大。

表1 染色体编码说明Tab.1 Chromosome representation
4.4 遗传操作
采用锦标赛法对个体进行选择操作。关于交叉和变异,本文采用算数交叉的方式和逆转变异的方法。改进遗传算法中采用自适应交叉概率Pc和变异概率Pm,当种群个体适应度趋于一致或局部最优解时,交叉和变异概率增加以跳出局部最优解;当群体适用度比较分散时。交叉和变异概率减少以利于优良个体的生存。自适应的交叉和变异的表达式为

式中:Pc1,Pc2,Pm1,Pm2分别为预先定义的参数;f为进行交叉的两个个体中较大的适应度值;f’为变异个体的适应度值;favg为每代种群平均适应度值;fmin为每代种群最小适应度值。
5 算例分析
根据某码头的统计数据设计算例,评价模型和算法的有效性。具体的数据为:码头岸线长度为1 500 m,配有13台岸桥,单个岸桥平均作业效率为30 TEU/(台.时)。计划时间周期为24 h,计划期内到港船舶总数为6艘。船舶具体信息见表2。
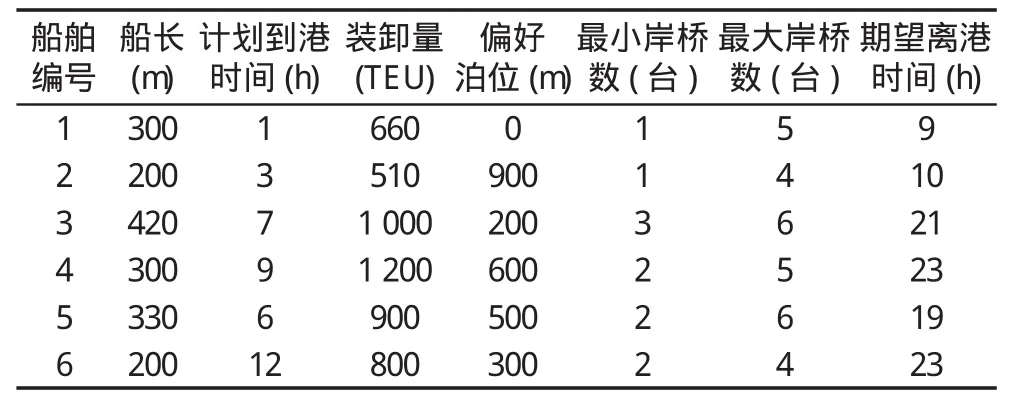
表2 船舶参数数据Tab.2 Data of the ships
为了保证码头作业的安全性,将船舶前后的安全距离取15 m,则船舶li的长度就包含了船长和安全距离。船舶的实际到港时间,服从以计划到港时间为均值的均匀分布,即到港时间服从[Ci-2.5,Ci+2.5]分布,通过计算得出相应的标岸桥的作业时间Bi服从以平均作业时间10.5小时为均值的均匀分布,即[6,15]分布。船舶实际信息如表3所示。

表3 船舶实际信息Tab.3 Actual information of the ships
在进行遗传操作时,选择Pc1=0.7,Pc2=0.3,Pm1=0.1,Pm2=0.07,根据改进的遗传算法计算后输出数据,计算的优化过程如图1所示,调度的结果如表4所示。

图1 算法进化收敛图Fig.1 Convergence of the algorithm

表4 泊位-岸桥调度结果Tab.4 Results of berth and quay-crane scheduling
6 结 论
集装箱码头的调度过程中存在诸多不确定因素,本文研究了在不确定环境下连续泊位与岸桥的联合调度问题,引入了多元服务质量损失函数建立优化模型,并采用改进的遗传算法对模型进行了求解。为验证模型的正确性,结合集装箱码头的统计数据进行了算例分析,得到了当到港船舶为6艘时的调度计划,在合理的时间内得了出了满意的解,使船舶在港总服务损失最小,进而提高客户满意度。计算结果表明,在目标函数中加入最大化的缓冲时间可以吸收作业中的不确定性,使方案更加可行、符合实际。
除此之外,在集装箱码头调度中,还应考虑到集卡、场桥及堆场集成调度等问题,在不确定因素的影响下合理地利用码头的各类资源,充分考虑各环节间的联系,制定合理的联合调度优化策略,这也是下一步的研究方向。
参考文献:
[1] Lu Z, LEE L H, CHEW E P. A decision model for berth allocation under uncertainty [J]. European Journal Research,2011,212(1):54-68.
[2] 陈秋双,杜玉泉,徐亚.不确定环境下集装箱码头的扰动管理[J].物流技术.2010,2(Z1):1-5. CHENG Q S, DU Y Q, XU Y. Disturbance Management of Container Ports under Uncertain Circumstances [J]. Logistics Technology, 2010, 2(Z1):1-5.
[3] Han X, Lu Z, X L, A .procative approach foe simulataneous berth and quay crane scheduling problem with stochasic arrival and handling time. European Journal of Operational Research [J]. 2010,207:1 327-1 340.
[4] 杨春霞.不确定环境下的集装箱码头泊位-岸桥调度优化研究[D].大连:大连海事大学,2011.
[5] 孙彬,孙俊清,陈秋双.基于鲁棒反应式策略的泊位和岸桥联合调度[J].系统工程理论与实践,201(4):1 076-1 083. SUN B, SUN J Q, CHEN Q S. Integrated scheduling for berth and quay cranes based on robust and reactive policy [J]. Systems Engineering-Theory & Practice, 2013, 33(4):1 076-1 083.
[6] 桂小娅.不确定性条件下集装箱码头泊位与岸桥集成调度计划建模与优化[D].上海:上海交通大学,2013.
[7] 粱承姬,吴宇.不确定环境下集装箱码头泊位与岸桥联合调度[J].计算机工程与应用,2015(11):1-9. LIANG C J, WU Y. Simultaneous berth and quay crane scheduling under uncertainty environments in container terminals [J]. Computer Engineering and Applications, 2015(11):1-9. CNKI网络优先出版:2015-11-04, http://www.cnki.net/kcms/detail/11.2127.TP.20151104.1600.002.html
[8] 艾延廷,田晶,高红池.基于多元质量损失与遗传算法的装配质量优化技术研究[J].中国机械程,2012,23(10):1 161-1 164. AI Y T, TIAN J, GAO H C. Study on Assembly Quality Optimization Techniques Based on Multivariate Quality Loss and Genetic Algorithm [J]. China Mechanical Engineering, 2012, 23(10):1 161-1 164.
[9] 匡芬,戴伟,陈亮,等.基于质量损失的加工过程可靠性评估方法研究和应用[J]. 计算机集成制造统,2015,21(6):1 571-1 574. KUANG F, DAI W, CHEN L, et al. Assessment method and applications for reliability manufacturing process based on quality loss [J]. Computer Integrated Manufacturing Systems, 2015,21(6):1 571-1 574.
[10] Yadav O P, Bhamare S, Rathore A. Reliability-based robust design optimization: a multi-objective framework using hybrid quality loss function [J]. Quality and Reliability Engineering International, 2010, 26(1): 27-41.
[11] 彭和平,蒋向前,徐振高,等.基于多重相关特征质量损失函数的公差优化设计[J].中国机械工程,2008,19(5):590-530. PENG H P, JIANG X Q, XU Z G, et al. Optimal Tolerance Design Based on the Quality Loss Function with Multi-correlated Characteristics [J].China Mechanical Engineering, 2008,19(5):590-530.
[12] Aytug H, Lawley M A, McKay K, et al. Ececuting proudution schhdules in the face of uncertainties: A review and some future directions[J]. European Journal of Operational Research,2005,161:86-110.
[13] 田口玄一[日].魏锡禄,王和福译.质量工程学概论[M]. 北京:中国对外翻译出版公司,1985.
Optimization of berth and quay-crane integrated scheduling in container terminal based on service loss function
WANG Zhi-ling, LIU Gui-yun*, LIU Ming-tao
(Faculty of Maritime and Transportation, Ningbo University, Ningbo 315211, China)
With the emergence of the uncertain environment, diversity and difference services, it needs to make an optimization of berth quay-crane integrated scheduling methods in container terminal to improve the efficiency and customer satisfaction. According to the resource allocation problem of berth and quay-crane in container terminal, by adding a buffer time to absorb the impact of uncertain factors on scheduling, based on the multiple service quality loss function, an optimization model was established aiming at the deviation of the optimum berth loss, move loss of quay-crane and ship time loss in port. Moreover, the improved genetic algorithm was used to solve the model, and the validity of the model and algorithm was proved by experiments.
uncertain environment; service loss; berth and quay-crane; customer satisfaction; genetic algorithm
U 651
A
1005-8443(2017)03-0313-07
2016-11-08;
2017-03-20
宁波市自然基金项目(2016A610074);浙江省软科学项目(2015C25039);宁波港口经济圈文化创新团队
王智灵(1991-),女,陕西宝鸡人,硕士研究生,主要从事港口及物流管理方面的研究。
*通信作者:刘桂云(1972-), 女, 满族, 辽宁鞍山人, 博士,教授, 主要从事港口和物流管理方面工作。E-mail: liuguiyun@nbu.edu.cn
Biography:WANG Zhi-ling(1991-), female, master student.

