基于TFPW-DT-ICSS法的渭河水文序列方差变异识别与诊断

张洪波, 张姝琪, 李吉程, 李娇娇

(1.长安大学 环境科学与工程学院,陕西 西安 710054; 2.长安大学 旱区地下水文与生态效应教育部重点实验室,陕西 西安 710054)

基于TFPW-DT-ICSS法的渭河水文序列方差变异识别与诊断

张洪波1,2, 张姝琪1, 李吉程1, 李娇娇1

(1.长安大学 环境科学与工程学院,陕西 西安 710054; 2.长安大学 旱区地下水文与生态效应教育部重点实验室,陕西 西安 710054)

水文变异现象已造成许多地区的水文数据受到“污染”,使得传统水文频率计算举步维艰。同时,水文变异识别方法的异法异解、隐藏效应、自相关性影响、变异信息交叉等问题也困扰着水文变异理论的发展,亟待解决。针对水文变异识别中的序列自相关性影响,提出将去趋势、预置白与ICSS检验法相结合,构建TFPW-DT-ICSS法,对渭河咸阳水文站的径流数据进行方差变异的多点识别，同时应用水文频率计算方法验证变异点的准确性。结果表明：TFPW-DT-ICSS法通过TFPW处理,可缓解序列自相关性对结果的影响；ICSS算法在方差变异检验上可获得较为准确的识别结果,适用于水文序列的方差变异诊断；ICSS算法对数据长度变化的响应不敏感,可实现多序列上的有效识别。研究成果可为变化环境下的水文计算与设计提供数据支持和技术支撑。

水文分析;变异点;自相关;径流;去趋势预置白算法;去趋势算法;迭代累积平方和算法

在气候变化和人类活动的强烈扰动下,水文要素发生了不容忽视的变化,并在全球范围内引发了一系列的水安全与环境安全问题[1],如极端事件与灾害频发、河川径流锐减、地下水枯竭、河道生态系统退化等,其常伴随着重大的经济损失,也使人类的生命安全受到严重威胁[2]。在学术界,这种现象常被称为水文变异,所发生的时间点为水文变异点[3]。所谓的水文变异是指在某种外界扰动下,水文序列特征(某一特征或多个特征)发生本质性的变化,即水文序列变异点前后的水文特性或分布类型存在显著差异,且这种变异并不同于水文学中常讲的水文变化或异常值。水文变化一般强调水文要素在某一平稳状态下呈现随机波动,且所有数据属于同一分布。异常值是指发生在水文时间序列中某一个或几个时刻上的超出原有变化范围的异常现象,剔除异常值后,水文序列仍然满足同一分布的要求;而水文变异与其有着本质的不同。水文变异是打破了原有的平稳状态,进入另一平稳状态或处于持续变化中。水文变异点之后水文序列系统状态有所改变,剔除变异点后序列并不能返回到原有的平稳状态。换句话说，水文变异是总体中的部分连续群体集体发生突变,而异常值是单点或多点突变现象。

由文献[4]可知,同一分布假设是传统水文计算理论的基础。基于该假设,水文现象才具有重现性,对历史水文数据的分析才能用来指导未来的水资源管理。然而当水文变异发生时,水文时间序列将不再满足该假设,而在统计特征上呈现出时变性,这无疑对传统的水文频率计算提出了巨大的挑战。那么,在变化环境下,如何进行水文设计与计算,以往的设计成果和运行策略是否存在潜在风险,这些关乎水利工程安全的问题必须被重新审视与论证。而水文变异的识别则是这一论证过程的关键与前提。

目前,水文变异识别主要包括两大内容,即判断水文序列是否存在变异和识别水文变异点的位置[5]。而识别的对象主要是水文特征,从狭义角度讲,一般包括均值、方差这两大统计参数,其直接影响着水文频率计算中的概率分布(国内一般为P-Ⅲ型),因此均值与方差变异也一直是当前水文变异领域研究的焦点[6-7]；而从广义的角度看,水文特征还包括回归趋势变化、周期变化、水文情势、自相关性、长程记忆性、系统熵值等。虽然已有学者对此作了相应的研究工作,但其并未形成国际上的广泛共识。

水文均值变异的识别一直是水文变异诊断研究领域的主流,许多方法陆续被引入到水文变异研究领域,如参数检验法、非参数检验法、贝叶斯方法、小波分析法等[6-7]。但在方差变异的识别上,国内外各领域中相关的研究方法并不多见。最早对时间序列方差变异点的研究始于HSU等[8]在1974年对证券市场价格平稳帕累托行为的研究,其提出用变方差正态分布模型来替代帕累托分布模型。后来在不同的研究领域陆续出现了贝叶斯比率(Bayes Ratio)、最大似然方法、自回归移动平均模型、迭代累积平方和算法(ICSS)、Sequential Regime Shift Detector(SRSD)等方法,均取得了不错的应用效果[9],但在水文领域的应用甚少。然而,水文序列中方差的变化极其重要,其对供水安全、河道生态保护都意义深远。因此，开展水文序列的方差变异诊断,对提高水文演变的预测能力,进一步认识与理解水文变异可能对人类社会产生的影响,尤其在应对环境变化所带来的潜在威胁上显得尤为必要。

鉴于此,本文将ICSS算法引入到水文序列方差变异识别领域中。但由于该方法假设条件为独立观测变量,且并未对序列中含有趋势的影响做出评估,故本文采用去趋势预置白算法(Trend-Free Pre-Whitening,TFPW)对序列进行预处理,剔除序列的自相关性干扰,再通过去除Pettitt均值跳跃检验的结果实现去趋势(Detrend,DT),最后应用ICSS算法实现方差变异的多点检测。

1 研究区概况与数据来源

渭河发源于甘肃省渭源县鸟鼠山,是黄河的最大支流,流经甘肃、宁夏、陕西3省,干流全长818 km。流域总面积13.84万km2,区内地形、地貌复杂,地势西高东低,西部为黄土丘陵沟壑区,东部为关中平原区。渭河流域地处干旱地区和湿润地区的过渡地带,气候特征鲜明。夏季炎热多雨,集中于6—9月,冬季干燥严寒,降雨稀少。多年平均降雨量572 mm,多年平均气温6～13 ℃,多年平均水面蒸发量660～1 600 mm。渭河水系发达,两岸支流众多,流域多年平均河川径流量100.4亿m3。然而,近几十年来渭河流域水文情势异常,径流面积衰减、泥沙淤积、河道生态退化、干旱频发等问题接踵而至。作为我国重要的粮油产区、“关天经济带”的核心区、“一带一路”建设的重要经济发展区,渭河流域的水安全问题尤为关键。开展渭河流域水文序列方差变异诊断对区域水资源安全与生态环境保护有重大意义。

本文主要选取渭河干流咸阳水文站1934—2009年的径流序列为研究对象,研究数据来源于陕西省渭河流域管理局。咸阳水文站地理位置如图1所示。

图1 咸阳水文站地理位置

2 研究方法

2.1 迭代累积平方和算法

迭代累积平方和(Iterated Cumulative Sums of Squares,ICSS)算法是INCLAN和TIAO[9]于1994年在改进了BROWN等[10]在1975年提出的累积平方和算法[13]的基础上,提出的一种对时间序列中存在的多个方差变异点进行识别的方法。该方法一经提出,便在金融等领域得到了广泛的推广[11]。具体原理如下:

设时间序列为x(t),t=1,2,…,N,令t1=1,t2=N,则序列可表示为x[t1∶t2],且其满足均值为0,方差为σ的分布。ICSS算法的计算过程主要分为两个部分:

1)基于累积平方和统计量的方差变异点检测。

步骤1 统计累积平方和,即:

(1)

步骤2 计算累积递归残差平方检验(CUSUM-SQ)统计量,记为：

(2)

步骤3 将CUSUM-SQ统计量中心化，即:

(3)

2)改进二元分割法。二元分割(Binary Segmentation,BS)法也称二分分段法,多用于图像分割处理与基因检测领域。ICSS算法中,二元分割法经改进后，作为ICSS的一部分,主要用来解决变异点识别中的多点识别问题。实质上,改进二元分割法主要是一种迭代检测的处理方法,通过分段检测和校验，完成多点识别的任务,其具体过程如下[9]:

步骤1 对序列x[t1∶t2]做基于累积平方和统计量的变异点检测,即test(x[t1∶t2]),如果存在变异点,位置记为k*,并转入步骤2a,否则认为该序列无变异点。

步骤2a 令t2=k*,test(x[t1∶t2]),如果存在变异点,位置记为ktop(i),并重复步骤2a,直到无法检测到变异点。其中,i表示步骤2a中的迭代次数。检测完毕后,令kfirst=t2。

步骤2b 用步骤1和2a继续检测步骤2a未检测的区域。令t1=k*+1,test(x[t1∶t2]),如果存在变异点,位置记为kbot(j),并重复步骤2b,直到无法检测到变异点。其中,j表示步骤2b中的迭代次数。检测完毕后,令klast=t1-1。

步骤2c 如果kfirst=klast,则说明原始序列中仅有一个变异点,即k*,算法结束。否则,令t1=kfirst+1,t2=klast,重新构造新序列x[t1∶t2],并重复步骤1和步骤2,直到找到所有时间序列中的变异点,即得到变异点集合CP。

步骤3 将集合CP进行排序,即sort(CP),并构建集合CP=[1,sort(CP),N]。M为集合CP中元素的个数,令m=1∶M,即顺序取值,并对x[CPm-1+1∶CPm+1]进行变异点检测,获得新的CP,重复以上步骤,直到变异点数目不再减少为止。并将此时的集合CP作为多点检测的最终结果。

2.2 去趋势预置白算法

由于ICSS算法要求待检序列为独立序列,因此需要对序列进行去除自相关的操作。目前,常用的剔除序列自相关性的方法主要包括两种:前置移除法和参数修正法。前置移除法常见的方法包括预置白处理(Pre-Whitening)法、去趋势预置白(Trend-Free Pre-Whitening)算法、过度白化(Over-Whitening)法等。本文采用去趋势预置白(Trend-Free Pre-Whitening,TFPW)算法对序列的自相关性进行剔除。TFPW是YUE等于2002年在处理序列自相关性对Mann-Kendall趋势检验[12-13]的影响时提出的一种去除序列自相关的预处理方法[14],在本文中其被用作序列的去趋势和ICSS变异点检测的前序处理。TFPW程序包括去趋势(Trend-Free)和预置白(Pre-Whitening)两个处理过程,可有效降低序列中自相关性对检验结果的影响,避免检验结果失真。具体步骤如下:

设一待检序列为Xt,t=1,2,…,m(m为序列长度),则有:

Yt=Xt-βt,

(4)

(5)

(6)

(7)

2.3 去趋势算法

研究表明,若序列中含有趋势成分可能会影响ICSS的检验结果。因此，在ICSS方差变异点检验之前,需引入Pettitt算法[15]进行均值跳跃检验,并剔除跳跃均值成分,也称去趋势(Detrend,DT),以保证ICSS算法的待检序列均值为零。为了实现均值跳跃变异的多点识别,本文将改进二元分割法(BS)和Pettitt算法相结合,以实现均值跳跃变异的多点检验。

3 结果与分析

3.1 TFPW处理结果

应用TFPW算法对咸阳站年径流序列进行偏自相关检验(Partial ACF),得到序列的各阶偏自相关系数,如图2(a)所示。由图2(a)可知,序列中存在较为明显的长程相关性,分别表现在4阶和19阶。为了进一步剔除自相关性达到ICSS算法的使用要求,先对其进行4阶自相关项的剔除,其结果如图2(b)所示。

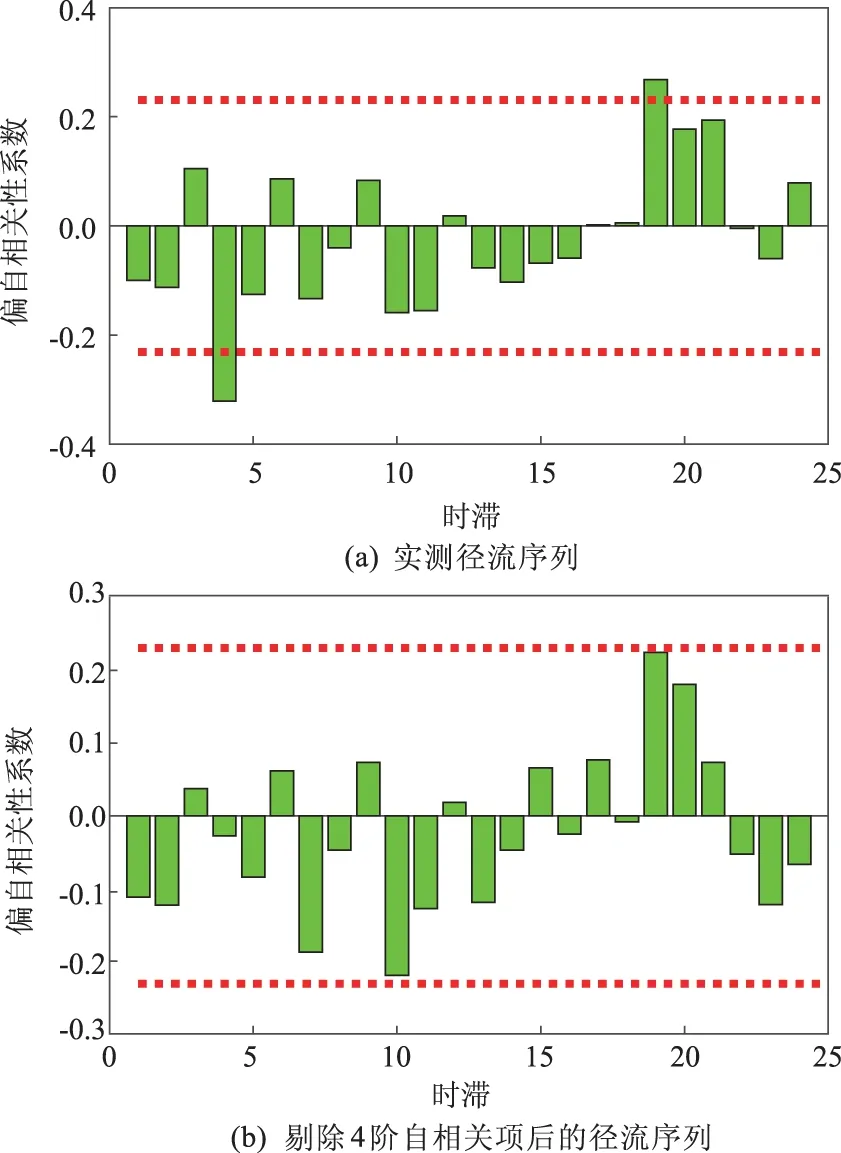
图2 咸阳站径流序列的PACF检测结果

由图2可知,经过4阶自相关项的剔除处理后,序列中的各阶自相关性均呈现不显著状态,故可认为此时的序列满足ICSS算法中数据独立的要求,可用于计算。

3.2 趋势检验与去趋势结果

将去自相关序列代入BS-Pettitt均值跳跃模型进行变异点检测,检测结果如图3(a)所示。结果显示，序列分别在1968年、1993年、2002年发生了显著跳跃变异。根据诊断结果,可将其分为1934—1968年,1969—1993年,1994—2002年,2003—2009年4个数据段。进而逐段消减其各段均值,使整个序列变成一个均值为0的新序列，结果如图3(b)所示,简称为去趋势序列(即扣除均值的干扰)。由图3(b)不难看出，其方差的变化较为明显,但是否有显著变异则需进一步检验。

图3 咸阳站径流序列变化

3.3 方差变异检验

将自相关性和趋势成分剔除后的径流序列代入ICSS算法进行方差变异点的多点检验,来检测统计量变化及变异点位置,检验结果如图4所示。图4表征了方差变异点前后去趋势去自相关序列数据的结构特征。由图4可知：整个去趋势序列中仅存在一个方差变异点,即1985年；变异点后数据的振幅大幅度缩小,极值差仅为原来的1/5；强烈的振幅变化表明变异点前后去趋势去自相关序列发生了较为明显的方差变异,即1985年应该是一个显著的方差变异点。

图4 ICSS检测统计量变化及变异点位置

为了验证该结果的准确性,将方差变异点前后两段数据进行方差标准化,即消除方差差异,再进行ICSS方差变异诊断。结果表明，方差标准化后,无变异点再被检出。遂可以得到结论:1985年为渭河咸阳站径流序列中唯一且显著的方差变异点。

箱图(Box-plot)是一种用作显示一组数据分散程度的统计图。通过箱图可分析出方差变异点前后径流序列的变化，结果如图5所示。由图5可知，变异点之前和变异点之后序列的50%频率所对应的流量值无太大变化，但变异点之后序列的25%频率和75%频率对应流量值之间的变化幅度明显小于变异点之前。

图5 统计量变化及变异点位置

以变异点之前序列的25%频率和75%频率对应的流量值为边界,对变异点后的数据进行频率值统计,结果见表1。由表1可知：在变异点1985年之前,大于25%频率值的年份有17 a,小于75%频率值的年份有16 a；而在1985年之后,大于25%频率值的年份仅有2 a,小于75%频率值的年份为3 a,这意味着河流中原有的枯水年和丰水年大量消失,可能会对河流造床、洪泛区营养补给、河道生物的迁徙等造成不利影响。

表1 变异点前后频率值统计 a

3.4 方差变异对频率计算结果的影响

为了检验方差变异对水文频率计算结果的影响,将去趋势序列加上1934—1968年的年径流均值,并对得到的重构序列分段(1934—1985年和1986—2009年)进行P-Ⅲ曲线的适线,结果如图6(a)和图6(b)所示,同时计算1969—2009年不同频率下的设计值，结果如图6(c)所示。

从图6中不难看出,方差变异导致两段序列的适线形态明显不同,具体表现为丰水期(年际)减小,枯水期(年际)增加,这与图5中所得到的结论完全相符。由此可见,当不考虑方差变异影响时,所选取的设计频率值很可能脱离实际,进而造成设计结果的偏差。而这无疑会对地区水资源供需平衡、水利工程运行安全以及生态保护战略的实施效果产生重大的影响。

图6 咸阳站重构径流数据的P-Ⅲ型适线结果对比

3.5 趋势成分和序列长度对检验结果的影响

众所周知,很多方差变异检验方法很容易受到序列趋势变化的影响。为检验序列中趋势成分对检验结果的影响,将原始序列去除自相关后,直接代入ICSS算法进行方差变异点的识别,结果如图7所示。由图7可知,在趋势成分(均值变化)的影响下,ICSS算法并未有方差变异点被识别出来,可见趋势成分对方差变异检验结果的影响是客观存在的。在ICSS应用中一定要注意提前去除趋势,以保证获得准确的方差变异检验结果。

除此之外,很多变异点检验方法对序列长度都有着一定的要求,对于靠近序列边缘的变异点则很容易被遗漏。为了验证ICSS算法在序列长度上的表现,本文从单侧(序首)逐渐缩短待检序列,并检测其变异结果,直到临近变异点。检验结果如图8所示。由图8可知，当距离变异点小于3个数据时,变异检测结果发生了变化,变异点位置消失。由此可见,ICSS对序列长度的变化并不敏感,当序列边缘与变异点的距离超过3时,即可实现准确识别。

图7 含趋势成分序列的方差变异检验结果

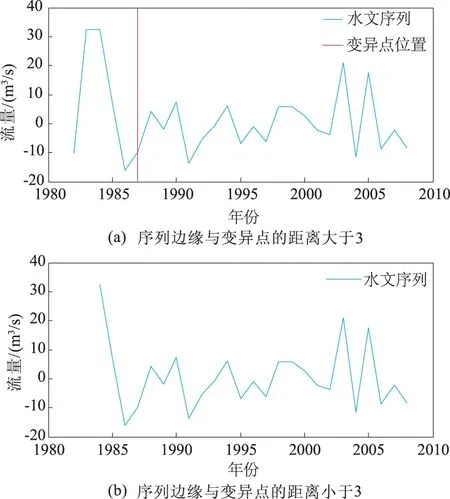
图8 序列边缘与变异点距离不同时的序列方差变异检验结果

4 结语

将方差检验方法ICSS算法引入到水文领域中,提出了TFPW-DT-ICSS耦合算法,用来解决受自相关性和趋势成分影响的水文序列的方差变异诊断问题。经分析与讨论,得出如下结论:

1)ICSS算法可较好地完成水文时间序列的方差变异诊断,但存在两个前提：去趋势与去除序列自相关影响。

2)方差变异与均值变异一样,是客观存在的水文变异现象,且其对频率计算产生的影响不容忽视。如欲由变异点位置确定近天然序列段,则必须在均值变异检测后,进行方差变异检测,以保障均值变异前时间序列未发生方差变异,方可认为其为近天然序列。

3)ICSS算法对序列长度的变化并不敏感,当序列边缘(前序)与变异点的距离超过3时,可实现准确识别。但受变异类型和特征的差异,有效距离可能略有差异,还需进一步分析。

在渭河咸阳站年径流序列方差变异的成因上，笔者认为方差变异的产生主要与流域水土保持治理、下垫面植被变化以及沿岸人们取用水的习惯有关。水土保持建设的影响主要集中在淤地坝和坡面治理上，其拦沙滞水作用使得流域产汇流时间变长，出流过程趋于平缓，反映到径流变化上则呈现出径流序列方差变小。下垫面植被变化的影响与上述作用基本趋同。而人类在河道取用水过程中通常遵循丰水多取、枯水少取的基本思路，这也导致取水过程与来水过程呈现同频变化，削峰填谷作用明显，以致径流序列的波动变小。但受资料所限，定量化的研究仍有困难，有待在未来进一步开展。

[1]MILLY P C D,BETANCOURT J,FALKENMARK M,et al.On critiques of “stationarity is dead:whither water management?”[J].Water Resources Research,2015,51(9):7785-7789.

[2]LIU C,ZHENG H.Changes in components of the hydrological cycle in the Yellow River basin during the second half of the 20th century[J].Hydrological Processes,2004,18(12):2337-2345.

[3]KUNDZEWICZ Z W,ROBSON A J.Change detection in hydrological records:a review of the methodology[J]. Hydrological Sciences Journal,2004,49(1):7-19.

[4]CHOW V T.Handbook of Applied Hydrology[M].New York:McGraw-Hill Book Co.,1964.

[5]CHEN J,GUPTA A K.Parametric Statistical Change Point Analysis:with Applications to Genetics,Medicine,and Finance[M].Boston:Springer Science & Business Media,2011.

[6]周园园,师长兴,范小黎,等.国内水文序列变异点分析方法及在各流域应用研究进展[J].地理科学进展,2011,30(11):1361-1369.

[7]张应华,宋献方.水文气象序列趋势分析与变异诊断的方法及其对比[J].干旱区地理(汉文版),2015,38(4):652-665.

[8]HSU D A,ROBERT B M,DEAN W W.On the stable paretian behavior of stock-market prices[J].Journal of the American Statistical Association,1974,69(345):108-113.

[9]INCLAN C,TIAO G C.Use of cumulative sums of squares for retrospective detection of changes of variance[J].Journal of the American Statistical Association,1994,89(427):913-923.

[10]BROWN,R L,DURBIN J,EVANS J M.Techniques for testing the constancy of regression relationships over time[J].Journal of the Royal Statistical Society,1975,37(2):149-163.

[11]HUANG B N,YANG C W.The impact of settlement time on the volatility of stock market revisited:an application of the iterated cumulative sums of squares detection method for changes of variance[J].Applied Economics Letters,2001,8(10):665-668.

[12]卢璐,王琼,王国庆,等.金沙江流域近60年气候变化趋势及径流响应关系[J].华北水利水电大学学报(自然科学版),2016,37(5):16-21.

[13]李蔚,陈晓宏,吴孝情.中国南方高度城市化地区气象干旱时空演变规律分析:以深圳市为例[J].华北水利水电大学学报(自然科学版),2016,37(3):11-18.

[14]YUE S,PILON P,PHINNEY B,et al.The influence of autocorrelation on the ability to detect trend in hydrological series[J].Hydrological Processes,2002,16(9):1807-1829.

[15]PETTITT A N.A non-parametric approach to the change-point problem[J].Applied Statistics,1979,28(2):126-135.

(责任编辑：张陵)

Detection and Diagnosis of the Change Points in Variance of Hydrological Time Series in the Weihe River Basin Based on TFPW-DT-ICSS Method

ZHANG Hongbo1,2, ZHANG Shuqi1, LI Jicheng1, LI Jiaojiao1

(1.School of Environmental Science and Engineering, Chang′an University, Xi′an 710054, China; 2.Key Laboratory of Subsurface Hydrology and Ecological Effect in Arid Region of Ministry of Education, Chang′an University, Xi′an 710054, China)

Hydrological variation occurring in many areas has caused the "contamination" of hydrological data and made the calculations of traditional hydrological frequency in a difficult position. Although some approaches have been put forward for hydrological variation detection, but many problems such as different solution from various ways, masking effect, autocorrelation impact, information confusion still hold back the development of modern hydrologic analysis theory, and the problems must be resolved. In the paper, for solving the problems caused by autocorrelation impact in the series during recognizing hydrological variation, combined the algorithms of Detrend (DT), Trend-Free Pre-Whitening (TFPW) and Iterated Cumulative Sums of Squares (ICSS), TFPW-DT-ICSS algorithm was constructed to detect the change points in the variance of annual runoff data at Xianyang hydrological station in the Weihe River basin，in TFPW-DT-ICSS algorithm, Iterated Cumulative Sums of Squares algorithm was employed to eliminate the influence of autocorrelation in the series, Trend-Free Pre-Whitening algorithm and Detrend algorithm were used to remove autocorrelation impact and trend components. Moreover, hydrological frequency calculation method was applied to verify the accuracy of the location of change points in the variation. The results show that in TFPW-DT-ICSS algorithm, Trend-Free Pre-Whitening algorithm can relieve the autocorrelation impact in the series, and Iterated Cumulative Sums of Squares algorithm can exactly recognize the change points in the variance in the series. Besides, it is found that the Iterated Cumulative Sums of Squares algorithm is insensitive to the change of the data length, and can do effective recognition almost without length limitation. The results in the paper can provide data and technical support for hydrological computing and design in changing environment.

hydrological analysis; change points; autocorrelation; runoff; Trend-Free Pre-Whitening algorithm; Detrend algorithm; Iterated Cumulative Sums of Squares algorithm

2016-12-09

国家自然科学基金项目(51379014)；陕西省科学技术研究发展计划项目(2014KJXX-54)；中央高校基本科研业务费专项资金(310829152018)。

张洪波(1979—)，男，辽宁康平人，教授，硕导，博士，从事水资源系统工程方面的研究。E-mail:hbzhang@chd.edu.cn。 张姝琪(1994—)，女，山西运城人，硕士研究生，从事水文学及水资源方面的研究。E-mail:1585503936@qq.com。

10.3969/j.issn.1002-5634.2017.04.007

TV123;P333.6

A

1002-5634(2017)04-0047-07