基于模型试验的导管架平台抗冰锥体优化设计

， ， ， ， ， ，

(1.中海石油(中国)有限公司 天津分公司， 天津 300452； 2.天津大学 建筑工程学院， 天津 300072)

基于模型试验的导管架平台抗冰锥体优化设计

关湃1，黄焱2，万军1，杜夏英1，肖辉1，吴景健1，陈希恰1

(1.中海石油(中国)有限公司天津分公司，天津300452； 2.天津大学建筑工程学院，天津300072)

对我国渤海导管架平台对称式和非对称式抗冰锥体在极端条件下的抗冲击性能进行模型试验研究，试验结果表明：非对称式结构抗冰性能更好。在此基础上，对抗冰锥体强度冗余度过大的问题进行结构优化，并通过ANSYS有限元计算，发现优化后的抗冰锥体结构强度满足要求。

导管架平台；抗冰锥体；冰载荷；模型试验；有限元分析；优化设计

0 引 言

近年来，海底油气资源的开发逐渐向高纬度海域转移，一批海洋石油平台在寒冷海作业。海洋平台设立在寒冷海域时，其工程设计的考量与其他海域不同，必须重点考量海冰对结构的作用，需建立合理的抗冰结构。已有研究结果[1]表明：天然海冰的弯曲强度低于其挤压强度，因而冰排发生弯曲破坏的冰载荷要低于同等条件下发生挤压破坏的冰载荷。因此，在寒冷海域的海洋工程结构的水线面处往往采用锥形或斜坡式的设计形式，以达到降低冰载荷的效果。

本文针对渤海海域导管架平台抗冰锥体结构进行研究，基于模型试验探究何种结构形式抗冰效果更有优势，并对结构构成进行相关优化，通过ANSYS有限元软件计算验证优化后的结构是否具有足够的结构强度。

1 抗冰锥体

图1 渤海JZ9-3 CEPD平台

目前，为降低冰载荷对结构的作用，抗冰锥形结构在寒区海洋工程设计中得到了广泛的应用。 1993年，世界上首座浮式锥形钻井平台Kulluk号在加拿大Beaufort海域投入使用，水线面处呈倒锥形。芬兰Bothnia湾内的Kemi-I灯塔上安装了正置式破冰锥体[2-3]。加拿大St Lawrence南湾的Confederation跨海大桥桥墩上安装了不同锥角的两段式正置破冰锥体[4]。我国渤海重冰区的导管架平台上也在桩腿潮差段位置安装了抗冰锥体。渤海某平台的结构形式如图1所示。相对于其他海洋工程结构上采用的单一式抗冰锥体结构来讲，我国渤海重冰区导管架平台安装的是正-倒锥组合体，这是由于水线面处布置紧凑导致设计中不具备充分调整抗冰锥体几何参数的条件[5]。目前，以上、下2部分结构是否对称为标准，渤海导管架平台的抗冰锥体可以分为2类：第1类是以JZ20-2 MUQ平台等为代表的非对称式抗冰锥体；第2类是以JZ9-3 CEPD平台等为代表的对称式抗冰锥体。本文首先对这2类抗冰锥体进行模型试验研究。

2 模型试验

2.1试验条件

图2 试验场景

本文中所有模型试验均是在天津大学冰力学与冰工程实验室内完成的。试验场景如图2所示。 试验中采用的模型冰是第2代尿素模型冰[6]，在缩尺试验中其物理量可以满足模型比尺的要求。试验中选取某平台所处冰区百年一遇单层冰条件，依据Froude和Cauchy相似准则[7]，取1∶10的几何缩尺比。目标冰厚、冰强度值与原型间的对比关系见表1。试验中选取5种冰速工况进行测试，分别为50 mm/s，100 mm/s，200 mm/s，300 mm/s，442 mm/s，其中442 mm/s对应该海域最大冰速。试验中考虑了2种水线面位置条件对试验结果的影响：最高天文潮水位(Highest Astronomical Tide, HAT)和最低天文潮水位(Lowest Astronomical Tide, LAT)。依据以上条件，针对对称式和非对称式的抗冰锥共进行20组试验。

表1 原型冰与模型冰的关键参数

2.2试验模型

试验模型是根据满足渤海某平台潮差段使用要求的2种形式的抗冰锥体，按1∶10的几何缩尺比对试验模型进行加工。抗冰锥体试验模型如图3所示。对称式与非对称式正、倒锥组合体的区别为：正倒锥角有所不同和非对称式锥体整体上移。试验水位条件如图3所示。在模型试验中，通过安装在模型顶部的测力传感器对每组试验中锥体模型上的冰力时程进行测量，并对冰力时程曲线进行统计分析。

图3 抗冰锥体试验模型

2.3试验结果分析

不同冰速下模型试验的冰力值如图4所示，可以看出：冰力极值均出现在最大冰速处。本文主要研究水平方向冰载荷的极值对结构的影响，因此，首先对模型试验水平向冰力极值进行统计，并与API-RP-2N规范推荐的锥体理论极值冰载荷进行对比分析，如图5所示，可以看出：由规范计算的理论极值冰载荷普遍高于试验值。目前，冰工程界普遍认为规范推荐算法较保守，尤其是在倒锥体情况下[8]，这与本试验测试结果一致。但模型1在最高天文潮水位的试验值远高于理论值，通过分析试验现象与冰力时程曲线可知：在模型1最高天文潮的试验过程中，抗冰锥正锥体表面与冰排发生接触，促使冰排向上发生弯曲破坏，但冰排上爬很短的距离后就会遇到直立段的桩腿结构，而此时冰排仍具有较大的能量，与直立段作用时发生挤压破坏，有大量的碎冰沫从接触区域喷出，如图6所示。观察模型1冰力时程曲线(图7)可以得出同样的结论：冰力时程曲线呈现紧密的锯齿状波动形态，这是挤压破坏的特征。观察冰力的均值可以发现：破坏过程中仍然有弯曲破坏的痕迹。由图5还可以看出：模型2在最高天文潮水位试验时的冰力极值远低于模型1的冰力极值，这是因为模型2的锥顶高程提高使得挤压破坏现象很难发生，此时，冰排主要发生弯曲破坏，径向裂纹与环向裂纹的交汇导致冰排的最终破坏，如图8所示。

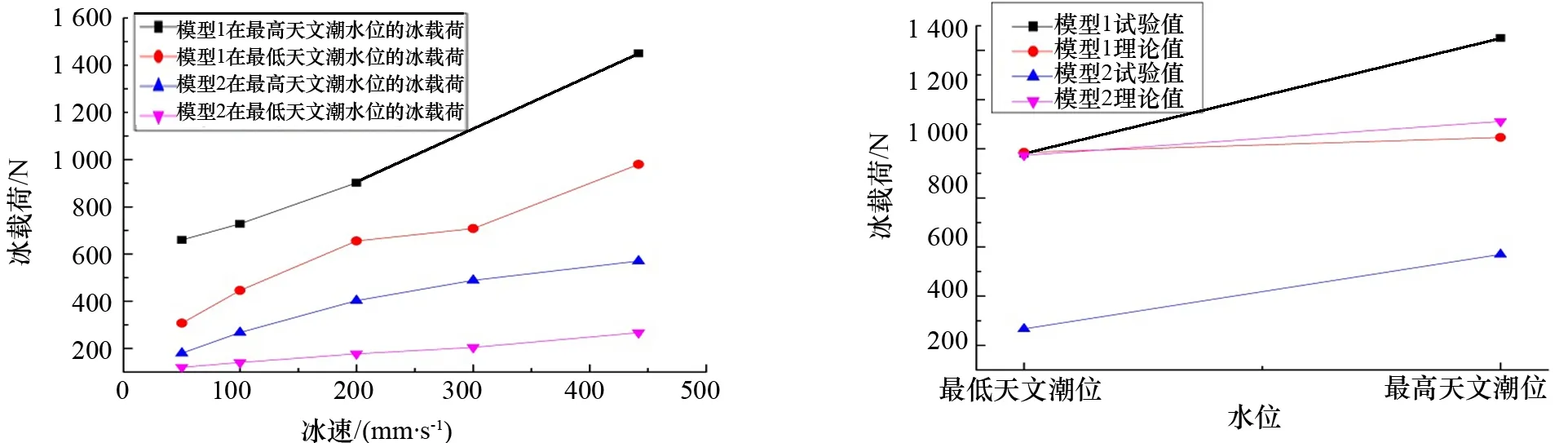
图4 不同冰速下试验冰载荷 图5 极值冰载荷对比

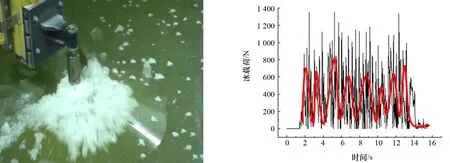
图6 模型1最高天文潮水位试验现象

图8 模型2最高天文潮水位试验现象

在最低天文潮水位试验条件下，模型1和模型2的理论极值冰力水平相当，但试验值相差悬殊。同样通过试验现象及冰力时程曲线分析其中的原因。冰排与模型1倒锥体结构接触后，首先呈现出向下弯曲变形的趋势，冰排内部并未出现径向裂纹，而是在距离冰与结构接触位置大约1.5倍锥体水线面直径的范围内，出现一系列环向裂纹。这些环向裂纹排列紧凑，并且处于相互交汇的状态，但这些环向裂纹的出现并未引发冰排的最终破坏，如图9所示。冰排的最终破坏集中在与倒锥体表面接触的局部位置，同时，这些局部破坏还伴有碎冰沫的涌出。此外，冰排通过倒锥体后保留的水道呈现出与锥体水线面边缘等宽的规则边界，表明冰排的破坏是完全沿着倒锥体水线面边缘出现的。这样的破坏痕迹通常出现在直立柱结构挤压破坏进程中。因此，可以认为冰排并未在锥体的引导下发生有效的弯曲破坏，导致冰排最终破坏的是挤压模式。但从冰力时程曲线(图7)可以发现：这种挤压破坏是区别于直立结构前冰排的挤压破坏。冰排在倒锥体引导下的向下弯曲变形促成了一系列环向裂纹的产生，这些弯曲变形区域内已形成了较大程度的损伤，这将极大降低冰载荷(同条件下挤压破坏冰力极值将达到1 590 N)。模型2的倒锥角度为53°，很好地引导了冰排发生弯曲破坏，冰排在倒锥体前有清晰的环向和径向裂纹，如图10所示，而这些是弯曲破坏的特征。从冰力时程中也可以观察到弯曲破坏的特征，如图11所示，在一个完整的冰力加载-卸载过程中，未出现幅值处于较高水平的连续波动。

图9 模型1最低天文潮水位试验现象 图10 模型2最低天文潮水位试验现象

图11 模型2最低天文潮50 mm/s冰速条件下冰力时程曲线

模型试验研究发现：模型2在抗冰性能上具有优势，主要表现为在最高天文潮水位时为上爬冰排留有一定空间，避免发生挤压破坏；在最低天文潮水位，相对较小的倒锥角可以有效地引导冰排发生弯曲破坏。

3 结构优化及有限元校核

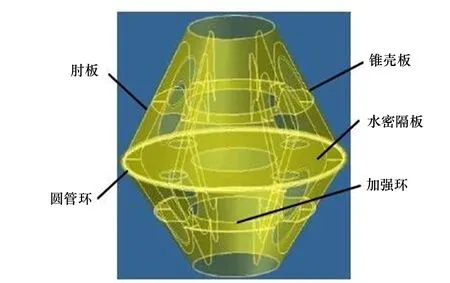
图12 抗冰锥结构组成

图13 抗冰锥有限元模型

模型试验研究发现：模型2具有更好的抗冰性能，因此在本节中选取模型2的结构进行优化及校核。抗冰锥的结构形式如图12所示，结构由锥壳板、水密隔板、加强环、肘板和圆管环组成。但该结构具有较大的冗余度，有必要进行结构优化。研究表明：降低各部分板厚、将肘板简化为角钢加强筋、取消加强环的设置后，结构可以满足强度要求。以渤海某抗冰锥为例，优化前后各构件尺寸见表2。

表2 优化前后构件尺寸 mm

3.1有限元模型

使用ANSYS有限元软件建立模型2的有限元模型，建模过程中使用Shell 63单元对腿柱、锥壳板、角钢加强筋和水密隔板进行模拟；使用Pipe 59单元对圆管环进行模拟。由于抗冰锥处于飞溅区及磨蚀区内，考虑腐蚀、磨蚀的影响，相应地扣除板厚8 mm。抗冰锥材料为DH 32钢，杨氏模量为2.08×1011Pa，泊松比为0.3，密度为7 850 kg/m3，屈服强度为315 MPa。导管架腿柱处定义为全约束。抗冰锥有限元模型如图13所示。

3.2校核工况

考虑3种极端冰载荷计算工况：第1种工况为冰载荷作用在最高天文潮水位(与模型试验相对应)；第2种工况为冰载荷作用在正倒锥交界面处；第3种工况为冰载荷作用在最低天文潮水位(与模型试验相对应)。最高和最低天文潮冰载荷按照模型试验测量值根据模型比尺还原到原型值进行加载，作用在交界面处的冰载荷保守考虑，认为冰排在该条件下发生纯挤压破坏，按照规范推荐直立结构的极值冰力进行加载。具体冰载荷见表3。锥面上冰载荷作用的高度范围为冰的厚度，水平方向范围为锥体迎冰面的180°。冰载荷在水平方向上为余弦分布，在z向上均匀分布，如图14所示。

表3 各工况冰载荷 kN

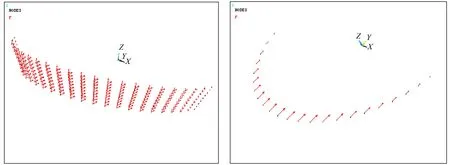
图14 冰载荷加载示意图

3.3校核结果

通过有限元方法计算3种工况的结构强度，如图15所示。许用应力取0.9倍的屈服强度，统计最大等效应力值及其出现的位置。各工况下的安全系数见表4。

结果表明：最大等效应力均出现在锥壳板上，在优化了板厚及肘板形式后，安全系数达到了1.50，非对称式的正倒锥结构具有足够的强度抵御极端冰载荷条件。

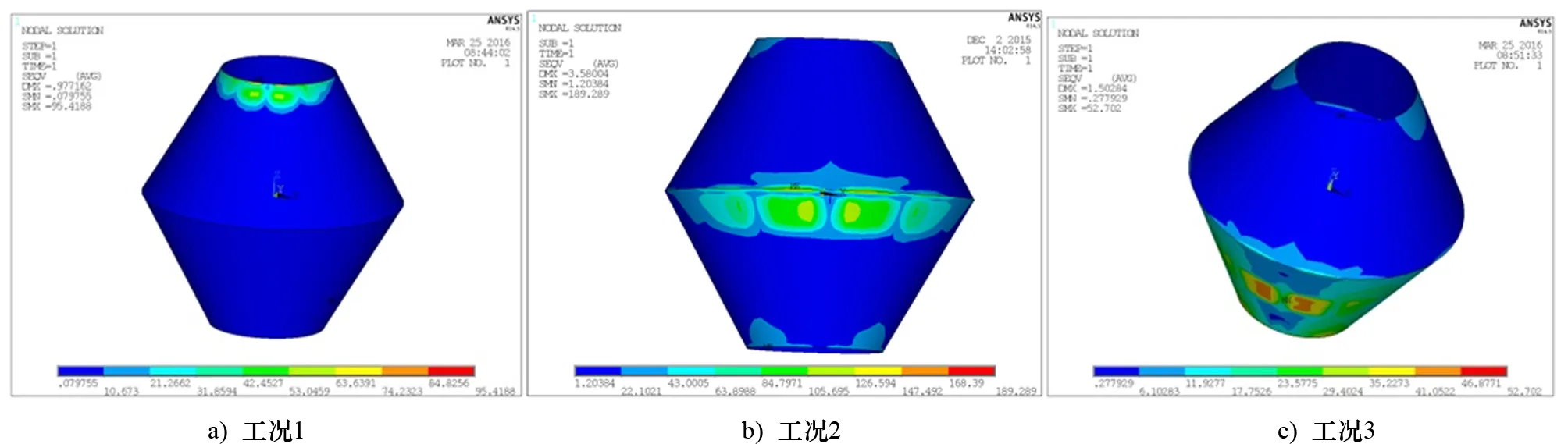
图15 有限元校核结果

表4 校核结果统计

4 结 论

本文对导管架平台抗冰锥结构进行模型试验及数值计算，得到以下结论：

(1) 非对称式的正倒锥组合体比对称式正倒锥组合体降低冰载荷的效果更好。

(2) 在设计中适当提升正锥体顶标高，以留给碎冰爬升的空间可以防止挤压破坏的发生，有效降低冰载荷对结构的作用力。

(3) 设计中尽量保持倒锥角在50°～55°，这样可以更好地引导冰排发生弯曲破坏，有效降低低水位情况下的冰载荷。

(4) 在模型试验的基础上，对非对称式正倒锥组合体进行适当的结构优化，在优化了构件板厚及肘板形式后，结构满足极端冰条件下的设计要求。

[1] RALSTON, T. Ice force Design Considerations for Conical Offshore Structures[C]// Memorial University of Newfoundland, Canada, 1977：741-752.

[2] 田育丰.覆雪水平对冰排与锥形结构相互作用进程的控制机理研究[D]. 天津：天津大学，2013.

[3] ENGELBREKTSON A， JANSON, E. Field Observations of Ice Action on Concrete Structures in the Baltic Sea[J]. Concrete International, 1985(08)： 48-52.

[4] BROWN T G. Confederation Bridge-An Innovative Approach to Ice Forces[C]//The Bridges for the 21st Century Session of the 2006 Annual Conference of the Transportation Association, Canada, 2006.

[5] 史庆增,彭忠.冰力作用下锥体的合理结构形式及在柱体上设计锥体的合理性探讨[J].中国海上油气,2005,17(05):342-346.

[6] 黄焱.冰激海洋平台振动的动力模型试验研究[D]. 天津：天津大学，2004.

[7] 史庆增,黄焱,宋安，等.锥体冰力的实验研究[J].海洋工程，2004，22(01)：88-92.

[8] HUANG Y, MA J J, TIAN Y F. Model Tests of Four-legged Jacket Platforms in Ice:Model Tests and Results[J]. Cold Regions Science and Technology，2013(95)：74-85.

OptimalDesignofJacketPlatforms’Anti-icingConicalStructuresBasedonModelTests

GUAN Pai1, HUANG Yan2, WAN Jun1, DU Xiaying1, XIAO Hui1, WU Jingjian1, CHEN Xiqia1

(1.Tianjin Branch of CNOOC Ltd., Tianjin 300452, China； 2.School of Civil Engineering, Tianjin University, Tianjn 300072, China)

Model tests are taken on symmetrical and non-symmetrical conical structures in extreme ice condition. Model test results show that the anti-icing performance of non-symmetrical conical structures is better. On the basic of model tests, the structural optimization is carried out for the problem that the redundancy of ice conical structures is too large. The strength of the optimized structure is verified to satisfy the strength requirements by the ANSYS finite element analysis.

jacket platform; anti-icing conical structure; ice load; model test; finite element analysis; optimal design

2016-03-29

关 湃(1989-)，男，助理工程师

1001-4500(2017)04-0007-07

F416

： A