一维二组元声子晶体结构参数的传递矩阵法反演研究

张振国，耿晓雯，刘 英，张 恒

（1.中原工学院 材料与化工学院，郑州 450007；2.郑州科技学院 土木建筑工程学院，郑州 450064；3.郑州大学 材料工程学院，郑州 450052）

一维二组元声子晶体结构参数的传递矩阵法反演研究

张振国1，耿晓雯2，刘 英1，张 恒3

（1.中原工学院 材料与化工学院，郑州 450007；2.郑州科技学院 土木建筑工程学院，郑州 450064；3.郑州大学 材料工程学院，郑州 450052）

采用声传递理论及传递矩阵研究方法，从反问题角度对无限周期一维二组元声子晶体进行理论研究和方法设计。从结构参数角度进行带隙研究，并进行计算机模拟。结果表明，可以从反演的角度对带隙进行研究，从结构参数角度研究无限周期的带隙，可以设计具有某个频率范围带隙的声子晶体隔声构件，从而为实际应用开辟一条新的途径。

声学；一维二组元声子晶体；声传递理论；反演；计算机模拟；结构参数

在目前噪声控制的研究中，隔声依然是一个主要的方法，多层板、夹芯复合板等层状复合结构依然是隔声的主要应用手段。截止到目前，对于层状复合结构能够进行定量分析的波动分析法以及能够进行定性分析的基于声子晶体理论的传递矩阵法，均从正问题角度进行研究[1–9]，即已知层状复合结构的材料物理因素(密度、声速、阻抗、刚度等)和结构因素（晶格常数、间距、组分比等），对隔声量和带隙进行研究，目前在理论和应用探索方面均取得较大进展。

然而，工程中最需要的是根据某一个具体的噪声环境进行噪声控制，设计出具有某个频率范围带隙（最大隔声量）的层状复合结构隔声构件。即从反问题角度，从带隙或最大隔声量所对应的频率出发，设计层状复合结构的物理参数与结构参数。鉴于层状复合结构涉及的物理因素与结构因素参数很多，研究起来比较复杂。因此，可以先固定一些因素，如物理因素，从结构参数的角度进行研究。文中即从这一角度针对该问题进行研究。

1 一维二组元声子晶体的模型与仿真计算方法

以一维二组元声子晶体，即由两种材料组成的一维声子晶体的研究为例，设两种不同密度和声速的材料A和B在x方向上交替排列，形成一维周期性复合材料结构[10]，如图1所示。

设该复合材料在各个方向均可无限扩展，没有边界约束。a1和a2分别表示材料A和B在一个原胞周期中的厚度，a=a1+a2为晶格常数，两种材料的密度分别记为ρ1、ρ2，材料A、B声波纵波速度分别用c1、c2表示。

这里只研究声波垂直入射的情况，波矢k与频率f之间的色散关系，即能带结构计算公式为

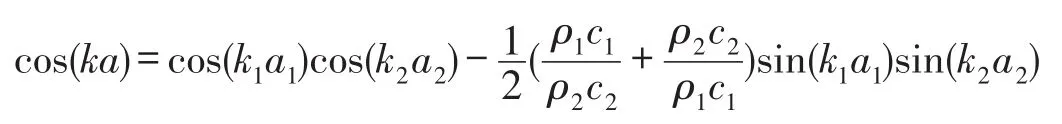
根据上述一维声子晶体能带结构的计算公式，利用matlab编写出相应的计算机程序，可以很方便地完成上述计算，并把计算结果绘制成波矢k与频率f色散关系图供分析对比。图2为钢和橡胶组成的一维声子晶体型复合材料的能带结构。钢和橡胶的材料常数如下：钢中的声速为5 960 m/s，密度为7 850 kg/m3；橡胶中的声速为96 m/s，密度为1 300 kg/m3；声子晶体的晶格常数为a=4 mm，组分比例为a1:a2=1。

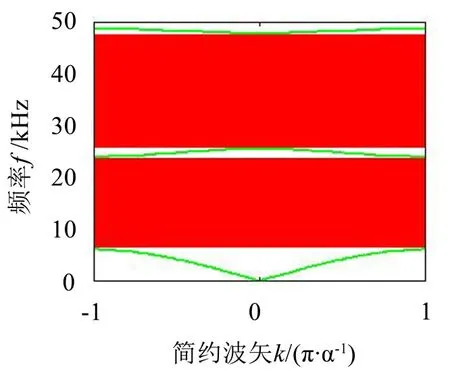
图2 钢与橡胶组成的一维声子晶体的能带结构

2 反演理论及公式的分析

已知一维声子晶体的组元材料密度、声速、晶格尺寸和材料组份，采用编制的计算程序，可以很方便地计算出声子晶体的带隙。然而，工程中最需要的是根据某一具体的噪声环境中噪声控制的需要，设计出具有某个频率范围带隙的声子晶体隔声构件。

2.1 理论分析

根据计算材料学的基本思路，应用等步长扫描法，给出一个可以把带隙作为已知条件来设计有限周期声子晶体型复合材料具体参数的方法。

已知一维声子晶体声波带隙条件下问题求解可归结为求解方程

则上式变成cos(ka)=Φ(f)

(1)对于给定的声子晶体，参数c1、ρ1、c2、ρ2、a、a1、a2已知，任给一个f值，由此式可计算出k值。cos(ka)为余弦函数，值域为[-1，1]，由此必有条件成立。此时，声波可以传播，频率f未在带隙内。

(2)任给一个f值，若有条件|Φ(f)|＞1成立，由于cos(ka)为余弦函数,值域仅为[-1，1]，则解答无意义，声波不可传播，f在带隙内。

2.2 计算方法设计

根据以上理论分析，设计计算方法如下：

(1)计算目标：给定一个频率fb，设计一种声子晶体型复合材料，使fb在其带隙内。

(2)计算方案设计：

1)输入带隙拟包含的频率fb；

2)输入声子晶体材料常数c1、ρ1、c2、ρ2；

3)根据声子晶体安装空间尺寸L，确定声子晶体周期数N和晶胞常数a。

L=Na

4)fb在带隙内的判据。

此时，对于任意一个x，x∈[ ]0，a，由上式的右边可以计算出一个Φ(fb)的值来。

① 输入0、a、h，其中h为步长；

②x=0时，计算Φ(fb)，检验是否大于1。如果是，则输出x=0；

依此类推。

对于任一步扫描，检查x=0+ih是否大于a。如果是，终止扫描。

如果整个数值范围之内都无法输出x值，缩小h值后重新扫描。如果仍然无法输出x值，只能更换材料，重新确定物理参数，再重新开始扫描计算。

|Φ(fb)|小于1，说明存在色散关系，存在相应的Bloch波矢与其对应；|Φ(fb)|大于1，说明不存在色散关系，不存在相应的Bloch波矢与其对应。而|Φ(fb)|的数值取决于材料A的厚度x，即研究材料A的厚度x与Bloch波矢k的关系，即可以确定是否存在带隙。当对应材料A的厚度x存在Bloch波矢k的值时，说明处于通带范围，当没有对应的值时，说明处于带隙频率范围。

3 复合材料设计实例

依然以钢和橡胶组成的一维二组元声子晶体型复合材料为例，来说明怎样用等步长扫描法设计声子晶体的带隙。

如前所述，二种材料的物理参数均已知。取晶格常数为a=4 mm，材料A钢厚度为x。设选择的带隙频率分别为4 000 Hz和7 000 Hz。图3和图4即为根据上述算法得出的材料A-钢厚度与Bloch波矢关系图。

由图3可知，在材料A的厚度范围，均有相应的Bloch波矢与其对应，即|Φ(fb)|小于1。因此，对于晶格常数为a=4 mm的钢和橡胶声子晶体，在整个晶格常数可能的范围内，无法形成带隙。

由图4可知，在材料A的厚度范围，既有相应的Bloch波矢与其对应，也有没有对应的，即|Φ(fb)|可以小于1，也可以大于1。因此，对于晶格常数为a=4 mm的钢和橡胶声子晶体，在材料A厚度为0.8 mm～2.9 mm的范围内，可以在7 000 Hz时产生带隙。

图3 4 000 Hz时材料A厚度与Bloch波矢关系图

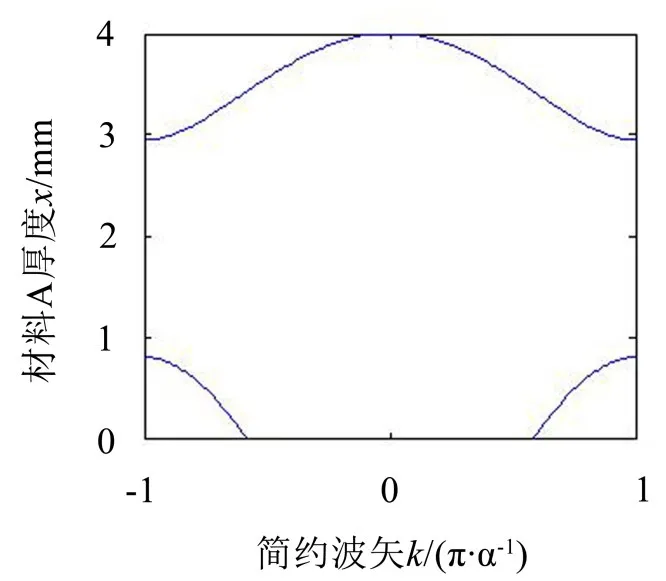
图4 7 000 Hz时材料A厚度与Bloch波矢关系图

4 复合材料能带验证

根据图3和图4可知，当材料A厚度为1.5 mm、材料B厚度为2.5 mm时，在4 000 Hz时不会产生带隙，而在7 000 Hz时会产生带隙。

这可以通过无限周期结构传递矩阵法的模拟计算来验证。图5为用传递矩阵法计算得到的钢与橡胶组成的无限周期一维声子晶体的能带结构图。由图5可知，在4 000 Hz时不会产生带隙，而在7 000 Hz时会产生带隙。

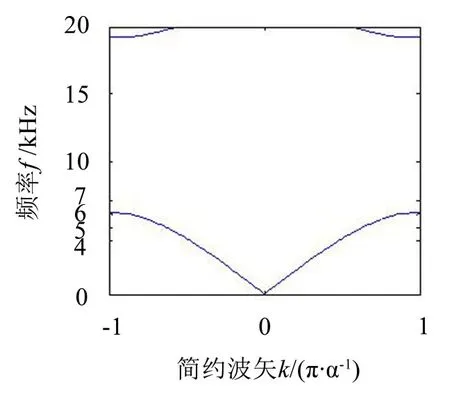
图5 钢与橡胶组成的一维声子晶体的能带结构

5 结语

针对一维二组元声子晶体，在从正问题角度研究带隙的基础上，可以从反问题角度对带隙进行研究。

从结构参数角度进行的研究表明，改变结构参数，会获得具有某个频率范围的声子晶体带隙。因此，可以根据某一个具体的噪声环境，设计出具有某个频率范围带隙（最大隔声量）的层状复合结构隔声构件。

[1]LEGAULT JULIEN,ATALLA NOUREDDINE.Sound transmission through a double panel structure periodically coupled with vibration insulators[J].Journal of Sound and Vibration,2010,329(15):3082-3100.

[2]MU RUI LIN,TOYODA,MASAHIRO,et al.Sound insulation characteristics of multi-layer structures with a microperforated panel[J].Applied Acoustics,2011,72(11):849-855.

[3]KURRA SELMA.Comparison of the models predicting sound insulation values of multilayered building elements[J].AppliedAcoustics,2012,73(6-7):575-589.

[4]陈卫松，邱小军.多层板的隔声特性研究[J].南京大学学报（自然科学），2005，41(1)：91-97.

[5]文钢，董华玉，张晓兵，等.多层均匀材料复合结构的声反射透射特性研究[J].武汉理工大学学报（交通科学与工程版），2008，32(5)：899-902.

[6]YU D L,LIU Y Z,WANG G,et al.Low frequency torsional vibration gaps in the shaft with locally resonant structures[J].Phys.Lett.A,2006,348(3):410-415.

[7]WANG G,WEN X S,WEN J H,et al.Quasi onedimensional periodic structure with locally resonant band gap[J].Journal of Applied Mechanics,2006,73(1):167-170.

[8]郁殿龙，温激鸿，刘耀宗，等.充液周期管路的轴向振动带隙特性[J].机械工程学报，2009，45(9)：36-40.

[9]蔡力，韩小云，温熙森.一维声子晶体振动带隙的带边模式研究[J].机械工程学报，2011，47(9)：90-96.

[10]张振国，刘英，张恒.基于声传递理论的层状一维二组元声子晶体的隔声降噪研究[J].材料导报，2013，27(169)：155-158.

Study on Bandgap of One-dimentional and Two-component Phononic Crystal Based on the Inverse Transfer Matrix Method

ZHANG Zhen-guo1,GENG Xiao-wen2,LIU Ying1,ZHANG Heng3
（1.College of Material and Chemical Engineering,Zhongyuan University of Technology,Zhengzhou 450007,China;2.College of Civil andArchitecture Engineering,Zhengzhou University of Science and Technology,Zhengzhou 450064,China;3.College of Material Engineering,Zhengzhou University,Zhengzhou 450052,China）

Based on sound transmission theory and transfer matrix method,the infinite periodic one-dimentional and two-component phononic crystals are studied in view of inverse problem.The computer simulations are carried out based on the structural parameters of the phononic crystal.The results show that the bandgap of the infinite periodic crystals can be studied in view of the inverse problem with structure parameters.The one-dimentional and two-component phononic crystal sound isolation components with the bandgap in a certain frequency range can be designed with this method.

acoustics;one-dimensional and two-component phononic crystal;theory of sound transmission;inverse problem;computer simulation;structure parameter

TB535

：A

：10.3969/j.issn.1006-1355.2017.04.036

1006-1355(2017)04-0185-03+226

2016-08-15

河南省科技厅国际科技合作项目(144300510063，152102410071)；河南省教育厅基础研究项目(13A430120)

张振国(1969－)，男，长春市人，博士，副教授。主要研究方向为声子晶体与噪声控制。

耿晓雯，女，郑州市人，硕士，讲师。主要研究方向为建筑材料与噪声控制。

E-mail:zhangzg1969@163.com