行星轮系动力学仿真分析与故障诊断
丁 闯,张兵志,冯辅周,任国春
(装甲兵工程学院 机械工程系,北京 100072)
行星轮系动力学仿真分析与故障诊断
丁 闯,张兵志,冯辅周,任国春
(装甲兵工程学院 机械工程系,北京 100072)
目前行星齿轮箱已经在军用和民用装备中广泛应用,研究行星齿轮箱的故障诊断方法意义重大。为了研究行星齿轮传动的故障机理,揭示其故障特征,本文建立了行星齿轮系统的动力学模型,研究了齿轮裂纹对齿轮啮合刚度的影响,得出了齿轮正常、太阳轮裂纹和行星轮裂纹等三种状态下系统的频率特征,总结了故障特征频率;最后试验验证了仿真结果的有效性,得出的故障特征频率可用于行星轮系的故障诊断。
振动与波;行星轮系;动力学模型;啮合刚度;裂纹损伤;特征频率;故障诊断
由于行星传动具有重量轻、体积小、传动比大、承载能力强、传动效率高等诸多优点,因此已被广泛应用于作战飞机、舰船、装甲车辆、自行火炮及风力发电和工程机械等军用和民用装备中。然而,在实际使用过程中,行星传动箱不仅承受重载负荷,且运行工况复杂多变,行星传动中的太阳轮、行星轮和齿圈等关键部件容易出现故障。而行星传动作为传动系中的关键系统,一旦出现问题没有及时发现将导致严重的后果[1]。
目前,国内外学者对定轴齿轮箱故障诊断进行深入研究,揭示了定轴齿轮箱故障的故障机理,提出一系列卓有成效的诊断方法,取得了丰硕的成果。然而行星齿轮箱的结构不同于定轴齿轮箱,其一般由太阳轮、多个行星轮、齿圈、行星架等组成,通常齿圈固定,太阳轮绕中心轴旋转,而行星轮不仅绕各自中心轴自转,同时绕太阳轮中心轴公转,行星排结构如图1所示。

图1 行星排结构
近年来,很多学者陆续对行星齿轮箱的故障诊断进行研究,Kahraman等提出单级行星齿轮系统的纯扭转模型,在考虑有限系统参数的情况下,得到系统的扭转固有频率方程[2];Parker等建立有限元分析模型,采用半解析有限元列式来进一步研究固有频率和振动模态问题[3–4];清华大学孙智民等通过建立封闭行星齿轮传动系统的动力学计算模型,获得系统的动态响应和动载荷系数的频域历程[5];宋轶民等揭示了3K-II型直齿行星齿轮传动的固有特性[6]。从国内外行星齿轮箱动力学建模方面的研究工作可见,现有的动力学模型是建立在很多假设基础之上,而且只是对正常行星齿轮箱系统建模,缺乏对齿轮故障时的建模,因此不能准确全面地反映实际行星齿轮箱的传动特性。且有关研究还停留在初步阶段,应用尚不成熟。
以某型装备行星变速箱某级行星排为对象,建立其动力学模型,揭示行星齿轮传动典型故障机理,分析在太阳轮和行星轮出现裂纹故障时系统的振动响应,在仿真结果的指导下得出行星轮系的故障频率,最后通过试验验证故障频率的正确性,使之可用于故障诊断。
1 行星轮系动力学建模
目前,建立的行星轮系动力学模型可分为数学模型、集中质量参数模型和有限元参数模型三类[7]。集中参数模型建模简单且最常见,在建模过程中,将各构件简化为集中质量,构件之间简化为弹簧和阻尼,从而将整个系统简化为经典的振动系统[8]。集中质量参数模型又可分为纯扭转振动模型和平移-扭转耦合振动模型两类。
Kahraman A于1994年发现,对齿轮传动系统建模时,当支撑刚度(轴承刚度、行星架刚度、齿圈刚度等)大于啮合刚度的10倍时,使用纯扭转振动模型代替平移-扭转耦合振动模型能达到较高的精度,满足实用需求[9]。由于文中所搭建的行星轮系的支撑刚度远大于啮合刚度的10倍,因此采用集中参数纯扭转模型,如图2所示,系统部件包括:太阳轮、行星轮、齿圈及行星架,将齿轮啮合视为弹簧和阻尼,每个部件只考虑扭转方向的振动。
图2中,Kspi、Krpi、Cspi、Crpi分别为太阳轮与行星轮、行星轮与内齿圈之间的啮合刚度和阻尼系数,θs、θpi、θc分别为太阳轮、行星轮和行星架的自转角度,TD、TL分别为输入扭矩和加载扭矩。
在实际运转中,行星齿轮传动以低转速重载荷为主,陀螺效应和离心力作用很小,此模型中不予考虑,根据拉格朗日方程,推导系统的纯扭转动力学方程可得

图2 行星齿轮传动纯扭转模型

方程组中的第1个方程式由对太阳轮进行动力学分析得到,第2个方程式由对每个行星轮进行动力学分析得到,第3个方程式是将N个行星轮和行星架作为一个整体进行动力学分析所得到的,行星轮与行星架之间的作用力为内力,式中的为N个行星轮和将行星轮作为一个整体对于行星架旋转中心的转动惯量,将行星轮和行星架作为整体进行受力分析,此整体共受弹性啮合力Pspi、Prpi、啮合阻尼力Dspi、Drpi以及扭矩TL的作用,而弹性啮合力主要由啮合刚度、支撑刚度(轴承刚度、行星架刚度、齿圈刚度等)决定,由于支撑刚度远大于齿轮啮合刚度,文中重点考虑齿轮啮合刚度及其变化,将行星架等支撑部件作为刚性体。式中,Is、Ipi、Ic分别为太阳轮、第i个行星轮及行星架的转动惯量,N为行星轮的个数,此处N=3,mpi为第i个行星轮的质量,mpirc2为第i个行星轮相对于行星架旋转中心的转动惯量。Pspi、Prpi、Dspi、Drpi分别表示太阳轮与行星轮、行星轮与齿圈之间的弹性啮合力和啮合阻尼力;rbc表示行星架的当量半径;rs、rpi分别为太阳轮和行星轮的基圆半径。
式(1)中含有角位移坐标,为了与弹性啮合力和啮合阻尼力建立关系,将角位移转换为相对线位移,假设太阳轮和行星轮在啮合线上的相对位移为xspi,行星轮与齿圈在啮合线上的相对位移为xrpi,如图3所示。
由图3可知

图3 太阳轮-行星轮和行星轮-齿圈啮合

此时,弹性啮合力Pspi、Prpi、啮合阻尼力Dspi、Drpi可表示为

将式(2)和式(3)代入式(1)并简化,系统动力学方程式(1)可表示为

Ms、Mpi、Mc分别为太阳轮、行星轮和行星架的等效质量。
此行星齿轮传动各部件的零件参数如表1所示。
2 裂纹故障对啮合刚度的影响
在行星齿轮箱故障诊断中,齿轮齿根裂纹是一种常见的故障,若不及时发现,其将扩展成断齿,将产生严重的后果。齿轮裂纹的故障识别一直是研究难点,研究齿轮裂纹故障诊断意义重大。因此,本文研究齿轮裂纹故障对系统响应的影响。
在损伤齿轮的裂纹轮齿进入啮合周期时,在此周期内的啮合刚度和啮合阻尼将发生变化,然而由裂纹引起的啮合阻尼变化对于系统的响应影响相对较小,因此重点考虑裂纹对啮合刚度的影响[10–11]。

表1 行星齿轮系统参数
2.1 正常齿轮啮合刚度
根据材料力学理论[12],啮合刚度和轮齿变形成反比,而在计算轮齿变形时,一般将齿轮轮齿作为悬臂梁处理,如图4所示。

图4 单齿悬臂梁示意图
轮齿变形由轮齿弯曲变形、压缩变形、剪切变形、接触变形以及轮体扭转变形组成[13],可通过以下公式计算:
弯曲变形

式中u为轮齿的横向弯曲变形;M(x)为作用在轮齿上的弯矩,M(x)=Fyx;E为齿轮材料的弹性模量;I(x)为轮齿截面的惯性矩,是x坐标的函数。
压缩变形

式中A(x)为轮齿的横截面积。
剪切变形
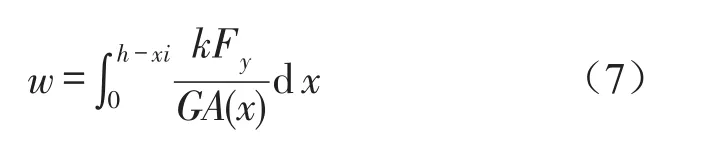
式中G为剪切弹性模量,为弹性模量和泊松比;K为截面形状系数,此处取为1.2[14]。
赫兹接触变形

其中

式中F为啮合力;W为齿宽;k1、k2为在啮合线方向上从啮合点分别到两齿轮中心线的距离;ρ1、ρ2为啮合齿轮的齿面在啮合点处的曲率半径。
使用Sainsot和Velex提出的公式计算基圆柔体变形
综上可得,在力F的作用下,齿轮中心线与啮合线交点A的总变形量为[12]

因此,轮齿任意位置i处的刚度可表示为

对于啮合的一对齿轮,可作为两个不同刚度的弹性元件串联,其啮合刚度为

在啮合过程中,多对齿轮对啮合可作为多个弹性元件并联计算。
2.2 齿轮出现裂纹时的啮合刚度
行星齿轮传动系统在长期工作后,轮齿根部将产生疲劳裂纹,研究发现,当齿根出现疲劳裂纹时,在裂纹处,单齿悬臂梁的横截面积发生改变,影响弯曲变形、压缩变形及剪切变形,引起齿轮啮合时的变形量发生变化,时变啮合刚度也将改变,最终导致传动系统的动态响应发生变化[15]。图5为齿轮轮齿裂纹示意图,齿轮裂纹贯穿整个齿宽,裂纹可使用裂纹位置d、裂纹角度β以及裂纹深度D表示。

图5 齿轮轮齿裂纹尺寸
由式(5)至式(11)通过数值方法计算得到,太阳轮轮齿裂纹故障状态与正常齿轮的啮合刚度对比如图6所示。由图6可知,轮齿出现故障时,系统的时变啮合刚度将会明显降低,且为周期非线性函数。
3 仿真分析
3.1 齿轮处于正常状态时的系统响应
设输入轴的转速为ni,在输出端施加负载M。行星轮、太阳轮、行星架的转频及齿轮的啮合频率可通过下式计算[16]。

图6 裂纹故障与正常齿轮啮合刚度对比
输入轴即太阳轮转频

行星架转频

行星轮转频

齿轮啮合频率

式中Z1为太阳轮的齿数,Z2为行星轮的齿数,Z3为齿圈的齿数。
设输入转速n1=1 200 r/min,将其代入式(12)至 式(15)中 ,可 得fs=20Hz,fH=3.33Hz,fp=5Hz,fm=333.3Hz。设驱动扭矩和负载扭矩分别为50 kN和100 kN,利用四阶龙格-库塔方法求解系统方程式(4)。图7为齿轮处于正常状态时系统的振动响应的时域和频谱图。由频谱图可知,系统响应以啮合频率及其倍频Nfm(N=1,2,3…)为主。

图7 齿轮处于正常状态时系统振动频谱
3.2 齿轮产生裂纹时系统响应
设输入转速、输入扭矩及加载扭矩均不变,太阳轮、行星轮齿根出现裂纹故障且裂纹位置d=5.6 mm、裂纹角度β=80°、裂纹深度D=1 mm。将裂纹参数代入啮合刚度计算公式,并使用四阶龙格-库塔方法求解系统响应,太阳轮出现裂纹、行星轮裂纹时振动信号的时域和频谱如图8(a)、图8(b)所示。
由图8可知,太阳轮和行星轮出现裂纹故障后,时域信号中出现了周期性的冲击信号,且裂纹损伤信号在频域中的啮合频率附近出现大量的边频。为了便于分析,求取两者的包络谱如图9(a)、图9(b)所示。
由图9可知,当太阳轮和行星轮出现裂纹故障时,包络谱结构的调制频率发生了变化,太阳轮、行星轮裂纹故障对应的故障频率分别为N(fs-fH)和N(fp+fH)(N=1,2,3…)。

图8 齿轮产生裂纹故障时系统的振动信号频谱
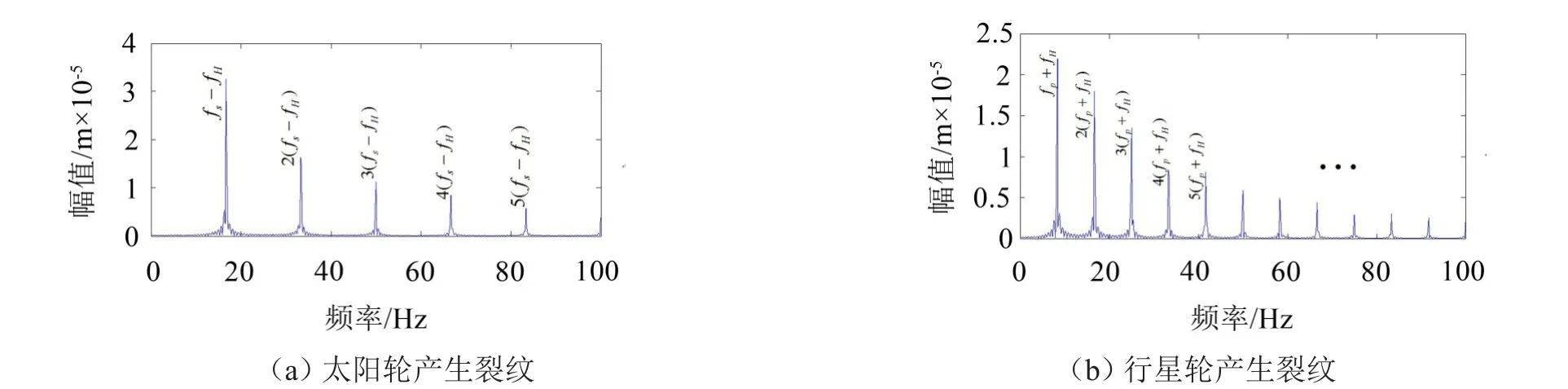
图9 齿轮产生裂纹故障时系统的振动信号包络谱
4 试验验证
分别对行星齿轮箱齿轮处于正常状态、太阳轮轮齿产生裂纹及行星轮轮齿产生裂纹三种状态进行故障模拟试验[15],试验台示意图如图10所示,其中行星齿轮箱中含有单一行星排,太阳轮为输入,行星架为输出。

图10 行星齿轮箱试验台
试验中,振动传感器粘贴在行星齿轮箱的箱体上,齿轮箱输入轴转速即太阳轮转速为1 200 r/min,采集齿轮在正常状态、太阳轮产生裂纹及行星轮产生裂纹时的行星齿轮箱振动信号数据,测试均在相同负载情况下完成。采集到三种状态的振动信号时域图和频域图如图11所示。由系统的时域振动信号可知,系统存在一定的冲击,但振动加速度的幅值明显增大,由于噪声及其他因素的影响,边频带集中在啮合频率和其倍频附近,故障信息并不明显,故障频率很难识别。

图11 三种状态振动信号的时域和频域波形
对三种状态信号求其包络谱,结果如图12所示。由包络谱图可知,在太阳轮发生裂纹故障和行星轮发生裂纹故障时,包络谱中可以找到特征频率分别为分别为仿真结果中的太阳轮故障频率和行星轮故障频率,而在齿轮处于正常状态时的包络谱中此特征频率并不明显。此结果验证了仿真的有效性。
5 结语
建立行星齿轮箱的动力学模型,研究齿轮轮齿裂纹对刚度的影响,分析故障对系统振动响应的影响,得出以下结论:
(1)当行星齿轮传动中的齿轮出现裂纹时,齿轮的时变啮合刚度周期性减小。

图12 齿轮振动信号包络谱
(2)太阳轮、行星轮出现裂纹故障时,系统的振动响应将发生变化。太阳轮发生裂纹故障时,振动信号的包络谱中将出现fs′=mfs±nfH(m,n=1,2,3…,)的频率成分,该频率为太阳轮转频的边频带,变频带之间的距离为fH,即前文描述的太阳轮故障频率;行星轮发生裂纹故障时,振动信号的包络谱中将出现fp′=mfp±nfH(m,n=1,2,3…,)频率成分,频率为行星轮转频的边频带,变频带之间的距离为fH,即前文描述的行星轮故障频率。
(3)由于各齿轮的故障频率不同,故而可根据故障频率定位故障源。
[1]雷亚国,何正嘉,林京,等.行星齿轮箱故障诊断技术的研究进展[J].机械工程学报,2011,47(19):59-67.
[2]KAHRAMAN A.Natural modes of planetary gear trains[J].Journal of Sound and Vibration,2004,173(1):125-130.
[3]AMBARISHA V K,PARKER R G.Nonlinear dynamics of planetary gears using analytical and finite element models[J].Journal of Sound and Vibration,2007(302):577-595.
[4]CHRISTOPHER G.COOLEY,ROBERT G.PARKER.A review of planetary and epicyclic gear dynamics and vibrations research[J].Transactions of the ASME.2014(66):1-15.
[5]孙智民,沈允文,李素有.封闭行星齿轮传动系统的动态特性研究[J].机械工程学报,2002,38(2):44-48.
[6]宋轶民,张俊,张君,等.3K-II型直齿行星齿轮传动的固有特性[J].机械工程学报,2009,45(7):23-28.
[7]巫世晶,王晓笋,胡建正,等.车辆行星传动系统虚拟样机技术研究与实践[J].中国机械工程,2005,16(6):550-553.
[8]程哲.直升机传动系统行星轮系损伤建模与故障预测理论及方法研究[D].长沙:国防科技大学,2011.
[9]程哲,胡茑庆,冯占辉,等.基于动力学仿真的行星齿轮系损伤检测方法[J].振动、测试与诊断,2010,30(4):379-383.
[10]桂勇,韩勤锴,李峥,等.风机行星齿轮系统齿轮裂纹故障诊断[J].振动、测试与诊断,2016,36(1):169-175.
[11]GUO YICHAO,PARKERGROBERT.Analytical determination of back-side contact gear mesh stiffness[J].Mechanism and Machine Theory,2014(78):263-271.
[12]刘鸿文.材料力学[M].北京:高等教育出版社,2004(7):81-83.
[13]李军,昝宝.装机车辆新型变速箱故障诊断研究[J].车辆与动力技术,2015(3):20-24.
[14]付宝连.弹性力学中的能量原理及其应用[M].北京:科学出版社,2004.
[15]孔德文.大型齿轮传动装置动力学及故障诊断技术研究[D].吉林:吉林大学,2008.
[16]冯志鹏,赵镭镭,褚福磊.行星齿轮箱齿轮局部故障振动频谱特征[J].中国电机工程学报,2013,33(5):119-127.
Dynamic Simulation and Fault Diagnosis of Planetary Gear Systems
DIND Chuang,ZHANG Bing-zhi,FENG Fu-zhou,REN Guo-chun
(Department of Mechanical Engineering,Academy ofArmored Force Engineering,Beijing 100072,China)
Nowadays planetary gearboxes have been widely used in military and civilian equipment.Study on fault diagnosis of planetary gearboxes is of important significance.In this paper,a dynamic model of the planetary gear transmission is built to study its fault mechanism and characteristics.The influence of the crack on the meshing stiffness is analyzed.The fault characteristic frequencies are studied under the three conditions,namely normal gear,cracked solar gear and cracked planet gear.Finally,the crack fault experiment is carried out on a test rig,and the results are employed to verify the correctness and effectiveness of the fault detection simulation.The provided feature frequencies can be applied to the fault diagnoses of planetary gear systems.
vibration and wave;planetary gear system;dynamic simulation;meshing stiffness;crack damage;feature frequency;fault diagnosis
TH212;TH213
:A
:10.3969/j.issn.1006-1355.2017.04.028
1006-1355(2017)04-0144-06
2016-12-13
装备预研基金资助项目(9140A27020115JB35001)
丁闯(1989-),男,河南省商丘市人,博士生,主要研究方向为行星齿轮箱状态监测与故障诊断。
冯辅周,男,博士生导师。
E-mail:fengfuzhou@tsinghua.org.cn

