基于Nastran的高速列车车体应力灵敏度分析

范乐天，管全梅，张庆刚，张锦华，孙龙宇

（中车唐山机车车辆有限公司 产品研发中心，河北 唐山 063035）

基于Nastran的高速列车车体应力灵敏度分析

范乐天，管全梅，张庆刚，张锦华，孙龙宇

（中车唐山机车车辆有限公司 产品研发中心，河北 唐山 063035）

随着高速列车种类的增加，对车体断面的适应性设计已进入深入性研究。针对某型动车组项目，基于Nastran通过有限元分析，将目前能调节车体强度等参数的方法（如加筋板、改材质、改壁厚等）的有效性和灵敏度，进行验证和归类，属于动车组车体断面设计领域较深入的一次探究，也为后续全面推进其他领域灵敏度分析提供参考。

高速列车；动车组；车体断面；Nastran；应力；灵敏度

0 引言

随着高速铁路的快速发展，高速动车组列车已成为人们出行的首选。车体强度作为保障运营安全的重要因素，在高速动车组车辆设计时需要着重考虑，在保障车体强度满足要求的同时，通过结构优化设计减少冗余，更好地实现轻量化设计[1-3]。灵敏度分析指一种用来评价因设计变量改变而引起结构响应变化率的方法。灵敏度是指结构的响应对设计变量的导数。在确立结构优化、可靠性评估和参数识别时，结构灵敏度是主要先决条件。20世纪70年代开始，有关灵敏度公式已经在许多文献中被报道[4-5]，为了提高求解效率，许多学者提出了灵敏度的半解析公式[6]。从结构响应的角度考虑，许多学者提出了不同的方法用于发展结构静态响应和结构动态响应的灵敏度计算[7]。白新理等[8]对于静力优化中的灵敏度采用基于有限元方程的解析灵敏度算法，其特点在于灵敏度精度高，计算耗时少；难点在于公式较复杂，程序实现难度大。为了分析不同位置板件厚度对车体性能的影响，采用Hypermesh软件建立某型动车组车体有限单元模型，计算车体整备情况下在主要工况时的应力。基于Nastran软件用数值微分法计算关键位置应力对主要板件厚度的灵敏度。

1 静强度分析

首先，对车体进行静强度计算，并计算应力灵敏度。通过计算分析结果，为响应位置的选取提供依据。

1.1 边界条件设置及计算工况选取

计算仅考虑整备情况。整备状态车体质量即指车体及车体附件（除转向架）质量，整备车体质量取32 t；其中铝合金车体质量约9.68 t，空调质量取1 t，加载时空调质量对应的载荷施加于空调框。计算只考虑落车约束，落车约束条件见图1，约束设置于模拟转向架与车体连接的4个刚性元主节点上：一位端一位侧节点的横向、纵向、垂向位移，一位端二位侧节点的垂向位移，二位端一位侧节点的横向、垂向位移，二位端二位侧节点的垂向位移。

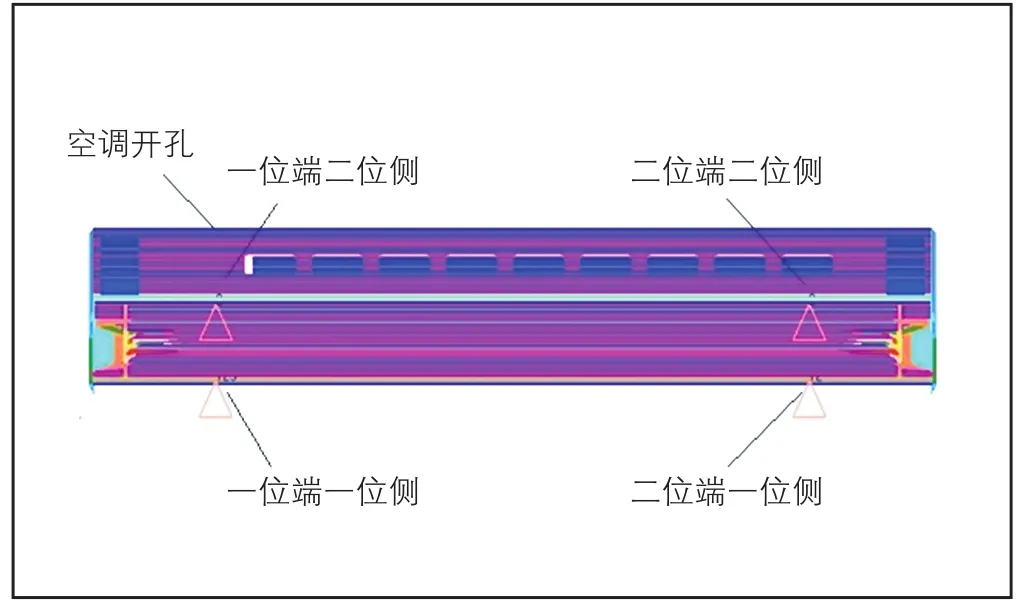
图1 落车约束条件

根据EN 12663—2010《铁道设备 铁道车辆车体结构要求》标准要求，选取拉伸和压缩2种典型工况进行静强度分析，并计算应力灵敏度。

1.2 计算结果

采用Nastran计算、HyperView做后处理。显示应力云图时采用Von Mises应力。以拉伸工况为例进行详细说明。整备状态时，中间车总质量为32.02 t，设备及附件质量为32.02-9.68=22.34 t，将设备及附件质量按1g转换成载荷施加在2/3地板，并在两端施加拉伸载荷。

纵向1 000 kN拉伸工况下，应力较大点分布在内端墙与地板连接处，牵枕缓结构及与其连接的地板部位，门角窗角处（见图2）；最大应力出现在二位端一位侧内端墙与地板连接处（见图3），最高应力为155 MPa；二位端二位侧上门角处应力最大值为53.25 MPa（见图4）。

1.3 小结

从静强度分析的Von Mises应力云图中可以看出，最大应力主要出现在各门角、窗角、地板中间部位、内端墙与地板连接处、牵枕缓冲梁与车体连接处。

图2 整体应力云图

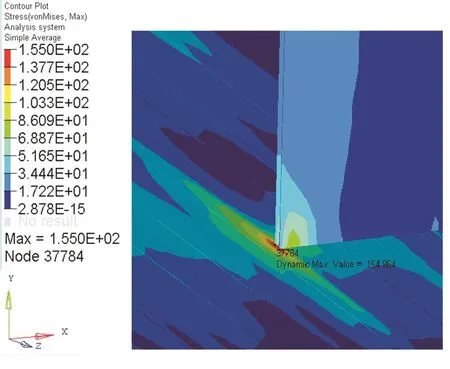
图3 内端墙与地板连接应力云图

图4 门角应力云图

2 设计变量和响应位置

2.1 设计变量选取

铝合金车体侧墙、地板、车顶和端墙都是由中空铝合金挤压型材拼接而成，将靠近车里的型材称为内板，暴露于车外的称为外板，型材中间交错的部分称为筋板。设计变量共有25个（见表1），相应位置见图5—图7。

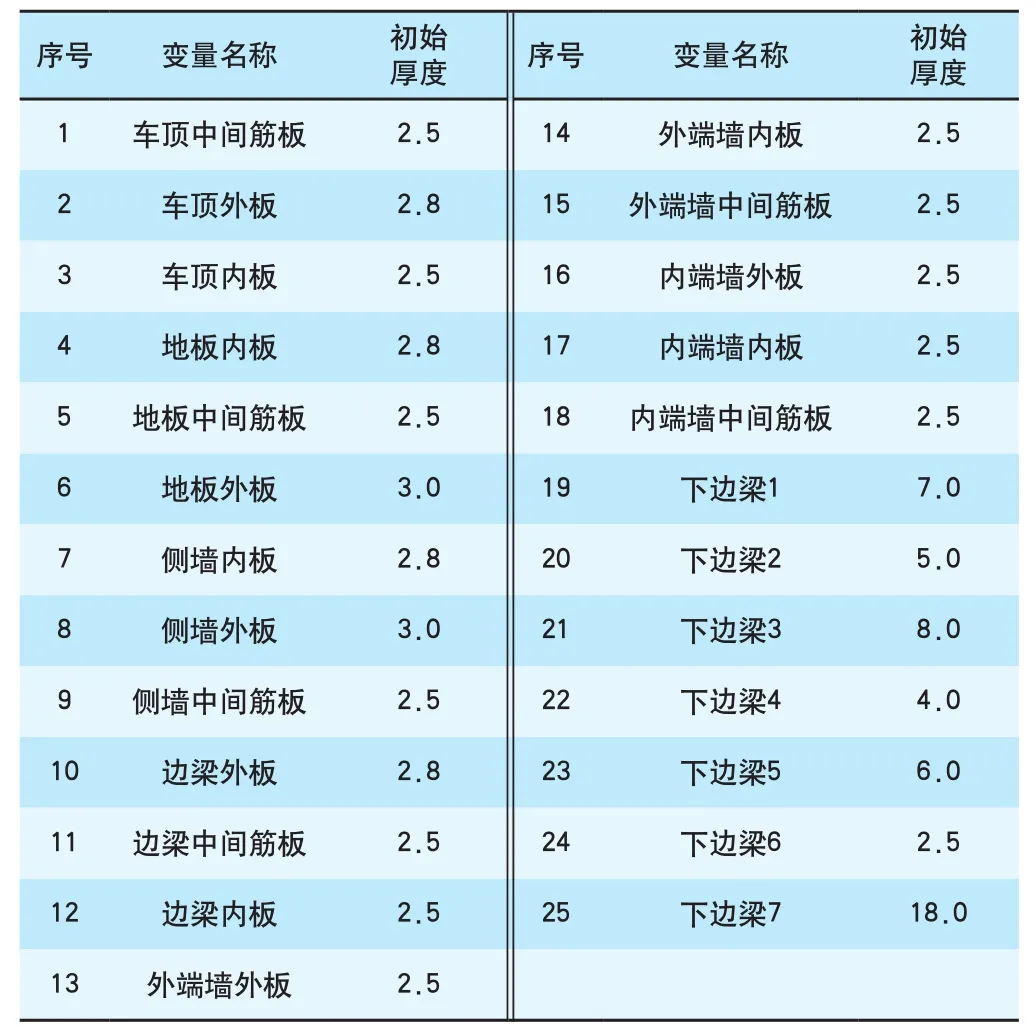
表1 设计变量序号、名称及厚度 mm

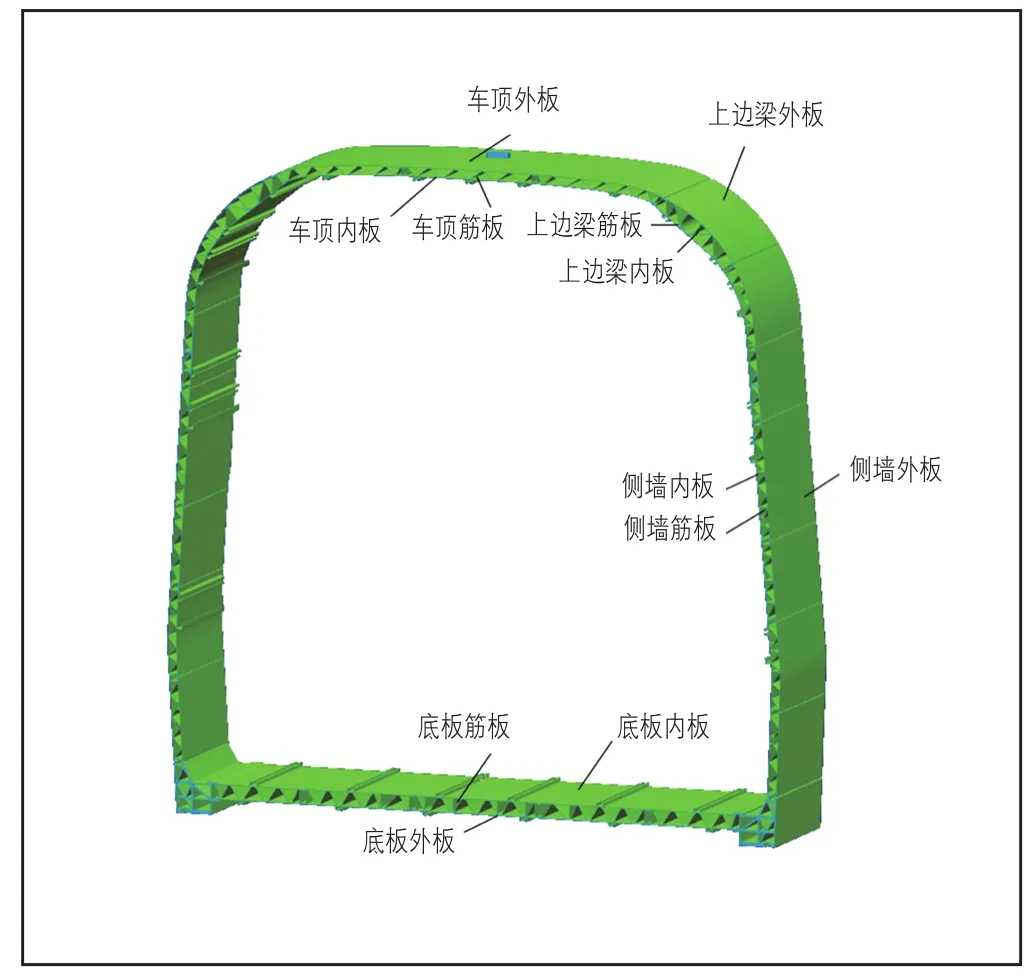
图5 部分设计变量位置示意图

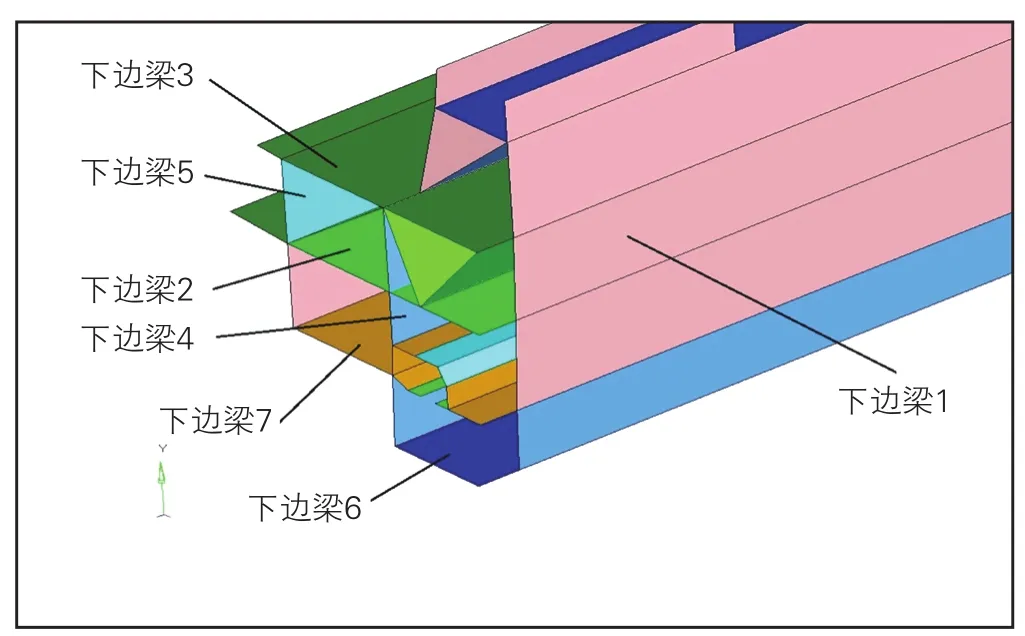
图6 下边梁局部示意图

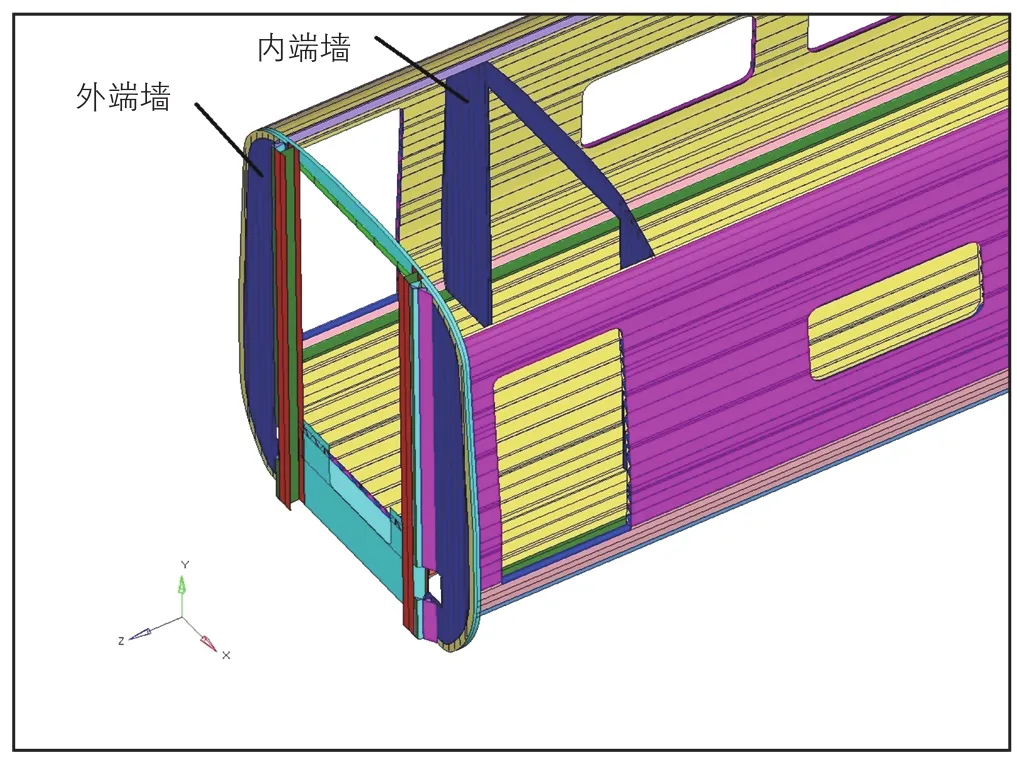
图7 内外端墙整体示意图

2.2 响应位置选取

响应位置选取静强度计算中应力较高区域，这些位置存在较大应力，单元具体选取最大应力和平均应力之间的单元（见表2），以尽可能消除应力集中对计算结果的影响。

表2 单元位置与拉伸工况应力值 MPa

3 整备状态下应力灵敏度

3.1 算法及原理

首先将结构进行离散，建立一个仅在节点处连接和仅靠节点传力的由有限个单元组成的计算模型。结构离散后，为了能用节点位移表示单元体内的位移、应变和应力，在分析连续体问题时，必须对单元中位移的分布做出一定假设，假定位移是坐标的某种简单函数，即位移模式或插值函数。选择适当的位移函数是有限单元法分析的关键。建立位移函数的常用方法是用形态函数来表达，简称形函数，它反映了单元内部各点位移分布的基本形态。根据选定的位移函数，就可以导出用节点位移表示单元内任意一点位移的关系式，其矩阵形式为：

式中：{u}为单元内任意一点的位移列阵；[N]为形函数矩阵；{δ}ɛ为单元的节点位移列阵。

当已知单元位移函数后，即可利用几何方程、物理方程导出用节点位移表示单元应变和应力的表达式，分别为：

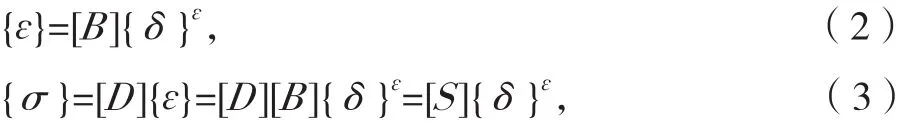
式中：{ɛ}为单元内任意一点的应变列阵；[B]为单元应变矩阵；{σ}为单元内任意一点的应力列阵；[D]为与单元材料有关的弹性矩阵；[S]为单元应力矩阵。

有了单元应力与单元节点位移间的关系式，即可根据单元的平衡条件，利用虚功原理建立单元节点力与节点位移的关系式，通常称为单元刚度方程组：

式中：{F}ɛ为单元的节点力矩阵；[k]ɛ为单元归纳刚度矩阵。

由于节点力是未知内力，上述单元刚度方程无法求出节点位移。因此，要求解节点位移，必须通过结构的整体分析建立起节点位移与节点载荷的关系式。根据各节点的静力平衡条件，即可建立起组合体所有节点的静力平衡方程式，将其汇在一起，并根据节点处的位移协调条件，即可推导出结构刚度方程组：

式中：[k]为结构刚度矩阵或总刚度矩阵；{δ}为结构所有节点的节点位移列矩阵；{P}为所有节点的节点载荷列矩阵。

这样就可以得到所有节点的位移，进而计算各单元应力等想要的结果。

式（5）对设计变量xj求导数，可得：

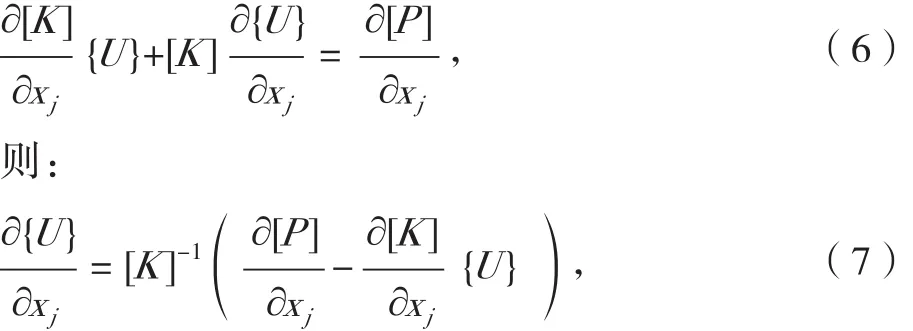
结构应力可以表示为结构位移的函数：

式中：{Q}为拟载荷。式（8）设计变量求导数得：

3.2 计算结果

通过Nastran软件将有限元模型及其参数带入，得出单元1—单元4的25个设计变量对应的灵敏度（见图8—图11）。

图8 单元1应力灵敏度

图9 单元2应力灵敏度

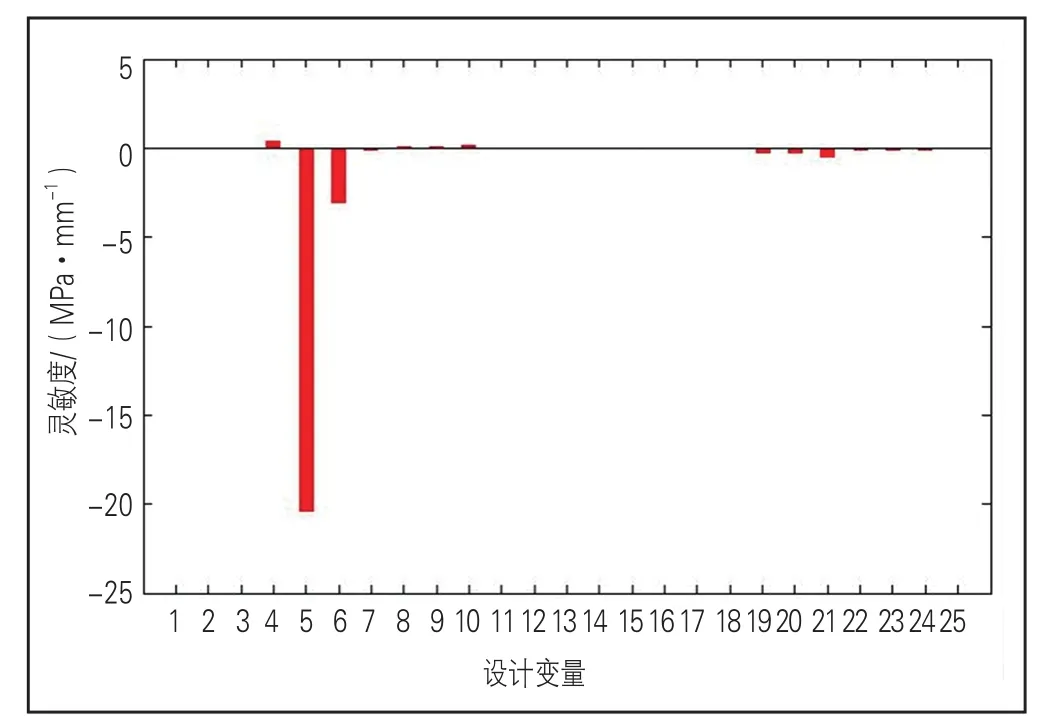
图10 单元3应力灵敏度

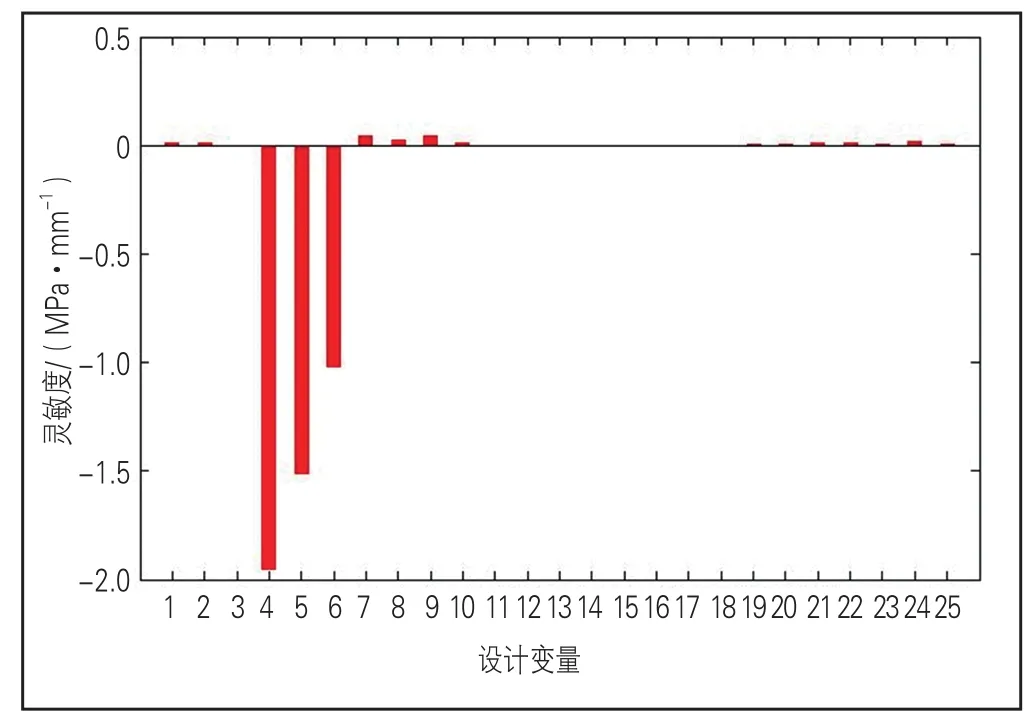
图11 单元4应力灵敏度

可以看出，单元1应力对侧墙内侧板、侧墙中间筋板、侧墙外侧板的灵敏度较大，对侧墙外侧板的灵敏度最大；单元2应力对车顶外侧板、地板外侧板、侧墙内侧板、侧墙中间筋板、侧墙外侧板的灵敏度较大，对侧墙内侧板的灵敏度最大；单元3应力对地板中间筋板、地板外侧板的灵敏度较大，对地板中间筋板的灵敏度最大；单元4应力对地板内侧板、地板中间筋板、地板外侧板的灵敏度较大，对地板内侧板的灵敏度最大。

4 应力灵敏度验证

为验证灵敏度计算的准确性，选取整备状态下的模态进行验证性计算。选取灵敏度数值较大的部位，增加其板材厚度，验证增加板材厚度后应力的变化，则其差分应力灵敏度为△λi,n=λi,xn+1-λi。△λi,n为第i个应力对第n个设计变量的差分灵敏度，λi,xn+1为第n个设计变量增加1 mm后的应力，λi为原结构应力。若计算的微分灵敏度和计算的差分灵敏度相等，则说明用微分法计算的灵敏度正确[9]。选取地板内侧板4、地板中间筋板5、地板外侧板6、侧墙内侧板7、侧墙外侧板8和侧墙中间筋板9作为验证的设计变量，板厚分别增加1 mm。

单元1和单元2在未增加板厚情况下的应力对所选设计变量灵敏度的大小见表3。

表3 单元1、单元2应力灵敏度

设计变量地板内侧板4、地板中间筋板5、地板外侧板6、侧墙内侧板7、侧墙外侧板8和侧墙中间筋板9分别单个增加板厚1 mm后，分别在拉伸工况下进行静强度分析，提取单元1和单元2位置的应力与未改变厚度前的应力值进行比较（见表4）。

表4 差分法计算的设计变量应力差值 MPa

将应力差值与对应的应力灵敏度差异进行整理，其差额最大值仅占原单元应力值的4.71%（侧墙中间筋板增厚1 mm后单元2处的应力变化），最小值仅占原单元应力的0.03%（地板外侧板增厚1 mm后单元1处的应力变化）。可以看出，灵敏度计算基本准确，但由于计算本身的误差，数据还存在一定误差。

5 结束语

综上所述，证明车体应力灵敏度的计算分析方法是初步可行的。依据车体灵敏度计算，对车体强度影响不显著的变量，可以通过结构优化设计减少冗余，对车体强度影响较大的变量可着重考虑。因此，采用车体应力灵敏度分析方法可优化车体结构设计，为车体结构的设计提供新的、有效的参考途径和优化方向。

[1] 安治业，赵红伟，田爱琴．新一代高速动车组车体 结构创新设计[J]．中国铁路，2014(10)：42-46．

[2] 才顺印，陈树娟，马纪军，等．高速动车组铝合金 车体设计方法探讨[J]．中国铁路，2014(5)：47-50.

[3] 鲁祥，马玉国，史丽萍，等．高速动车组铝合金车体 加工工艺创新[J]．中国铁路，2013(增刊)：15-20．

[4] 唐明裴，阎桂平．结构灵敏度分析及计算方法概述[J]. 中国铁道科学，2003，24(1)：74-79．

[5] 张传立，邹时智．结构动力响应灵敏度分析的 Laplace变换法[J]．华中理工大学学报，1995， 23(7)：27-30．

[6] 蔡则彪，郑铁生．特征向量敏度分析的快速方法[J]. 计算结构力学及其应用，1991，8(1)：93-100．

[7] 赵衍刚，孙景江．结构动力灵敏度分析中的几个问 题[J]．地震工程与工程振动，1991，11(4)：28-38.

[8] 白新理，梁醒培．渡槽结构优化设计的解析灵敏度 算法[J]．工程力学，2000(增刊)：31-35．

[9] 齐沛赛，张凌霞．基于灵敏度分析的结构动力模型 修改[J]．航空学报，1992，13(9)：472-475．

责任编辑 高红义

Nastran-based Analysis on Stress Sensitivity of Carbody for High Speed EMU

FAN Letian，GUAN Quanmei，ZHANG Qinggang，ZHANG Jinhua，SUN Longyu
（Products R&D Center，CRRC Tangshan Co Ltd，Tangshan Hebei 063035，China）

Along with the diversifcation of EMU categories, deep research on adaptability of carbody crosssection is started. Based on a EMU project, the efectiveness and sensitivity of the methods used for adjusting carbody strength (such as adding steel bars, changing material and adjusting wall thickness) are verified and classified by means of finite element analysis method based on Nastran. This is a probe into the design of carbody cross-section, and provides references for analysis on sensitivity in other felds later.

high-speed train；EMU；carbody cross-section；Nastran；stress；sensitivity

U270.2

：A

：1001-683X（2017）06-0053-06

10.19549/j.issn.1001-683x.2017.06.053

2016-12-23

范乐天（1982—），男，高级工程师。

E-mail：sjc-fanletian@tangche.com