数据库中关系代数除法运算的教学研究

李正欣+李克武+张晓丰+刘文杰

摘 要：關系代数中的除法运算是数据库课程中的难点问题。文章从关系代数除法运算的定义出发，以实例为牵引，通过类比整数的除法运算，阐明关系代数除法运算的本质，给出除法运算的基本运算表达方法并用SQL语句实现，突破除法运算的难点，以期取得较好的教学效果。

关键词：关系数据库；关系代数；除法运算；SQL

0 引 言

数据库技术基础及应用是信息技术领域的骨干课程，具有理论基础强和实践应用性突出的特点。关系代数是数据库原理的核心部分之一，在整个课程体系中具有重要作用。关系代数以集合论为理论基础，可分为传统的集合运算——并、差、交、笛卡尔积，专门的关系运算——投影、选择、连接、除法[1]。在8种运算中，除法运算复杂、抽象，是教学环节中的难点问题，也使得学生理解起来比较困难。

1 除法运算的过程详解及示例

1.1 基本定义

给定关系R（X， Y）和S（Y， Z），其中X、Y、Z为属性组， R中的Y与S中的Y可以有不同的属性名，但必须出自相同的域。R与S的除法运算得到一个新的关系P（X），P是R中满足下列条件的元组在X属性列上的投影：元组在X上分量值x的象集YX包含S在Y上投影的集合[2]，即

其中，YX表示x在R中的象集，x=tr[X]。

对于这一知识点，教材主要从概念方面进行描述，学生掌握起来比较困难。我们在非计算机专业的本科教学过程中，通过形象化的实例和深层次的分析，帮助学生透彻理解和掌握这一内容。

1.2 过程详解

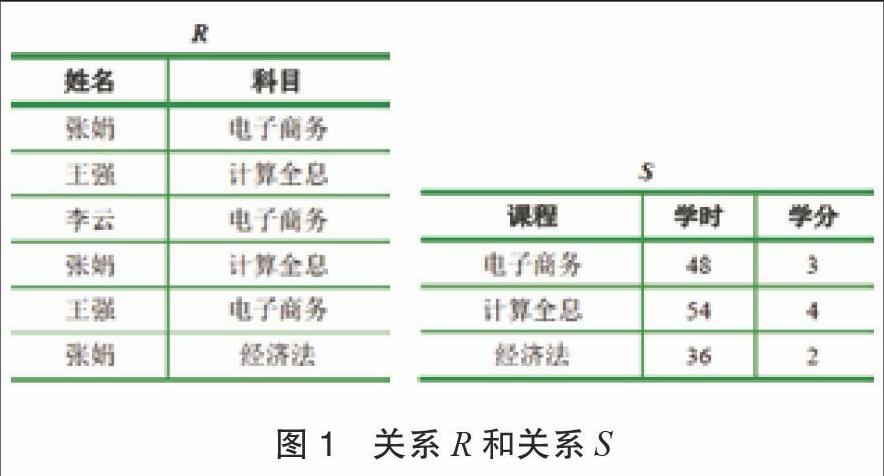
通过实例说明除法运算的求解过程，关系R、S如图1所示，计算R÷S的结果[3]。

第一步，明确除法运算定义中X、Y、Z对应的属性组。在关系R（姓名，科目）和关系S（课程，学时，学分）中，X={姓名}，Y={课程}或{科目}，Z={学时，学分}。

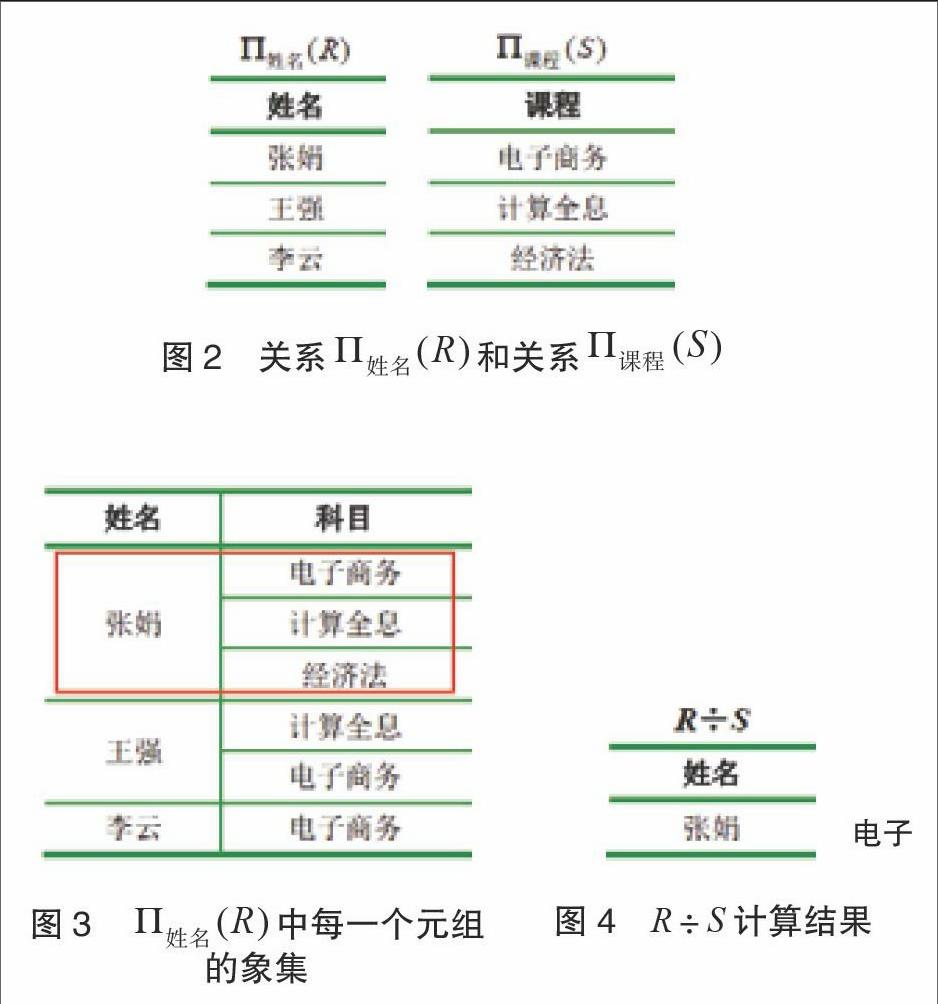
第二步，确定结果的关系模式。运算结果的关系模式为P（姓名），结果关系的每一个元组都包含在中，如图2所示。

第三步，计算。本例中的计算结果，如图2所示。

第四步，确定象集YX。在关系R中，依次确定中（如图2所示）每一个元组的象集，结果如图3所示。

第五步，比较与象集YX的关系，得到除法运算结果。仅有“张娟”对应的象集满足，如图3所示，因此可得R÷S的计算结果，如图4所示。

1.3 除法运算的含义

从语义上理解除法运算的含义，本例中表示所有的课程名称，运算结果的关系模式为P（姓名），表示学生姓名，因此R÷S表示在关系R中找出选修S中所有课程的学生。

为了便于理解，我们用整数除法作类比。两个整数R和S，R÷S是满足式（1）条件的最大整数P。

在关系代数中，除法运算R÷S是满足式（2）条件的最大关系实例P，即P与的笛卡儿积包含在关系R中，其中。

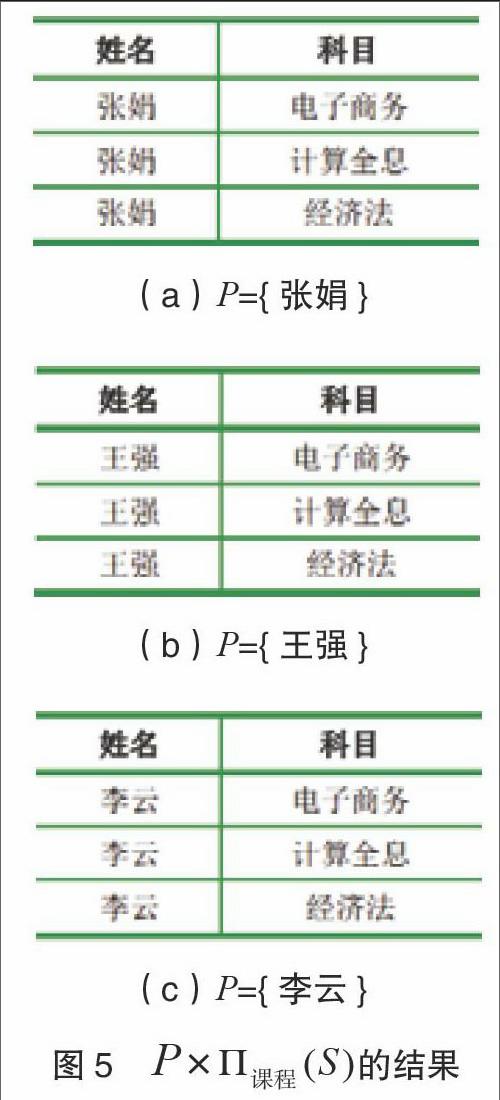
在本例中，包含3个元组{电子商务，计算全息，经济法}。当P分别为{张娟}、{王强}、{李云}时，的结果如图5（a）—5（c）所示，只有图5（a）的结果包含于R，因而P={张娟}是满足条件式（2）最大的关系实例，即是R÷S的结果。

2 用非基本运算表示除法运算

除法运算属于非基本运算，可以用基本运算进行等效表达，见式（3）。表达式形式抽象、烦琐且教材大多对这一内容描述简单，学生理解记忆起来比较困难[4]。教学中可利用实例，把抽象问题具体化，寻求对该知识点的突破。

实例中，R÷S表示“关系R中选修了S中所有课程的学生姓名”，用基本运算求解。

第一步，计算R的投影，实例中 表示所有学生的姓名。

第二步，计算S的投影，实例中表示所有课程的名称。

第三步，计算T×C中不在R中的元组V=T×C-R，实例中T×C表示关系“所有学生都选修了全部课程”，T×C-R表示“没有选修全部课程的学生”。

第四步，计算V的投影，实例中表示“没有选修全部课程的学生姓名”。

第五步，得出结果P=T-W，实例中P表示“选修全部课程的学生姓名”。

综合以上步骤可得式（4），它表示“关系R中选修了S中所有课程的学生姓名”，等价于表达式R÷S。

3 用SQL语句表示除法运算

关系代数是一种抽象的查询语言，是SQL查询的理论基础。用SQL查询实现关系代数中的除法运算，通常可使用带有EXISTS谓词的子查询表示[5]，该部分内容也是SQL查询中的一个难点，查询语句格式如图6所示。

SQL中没有全称量词，具体实现时，可以用双嵌套NOT EXISTS实现带全称量词的查询。与实例等价的自然语义是输出这样的学生学号——不存在某门课程，在他的选课记录里没有选这门课。通过自然语义，对应的SQL语句设计如图7所示。

4 结 语

除法运算的定义十分抽象，学生理解起来比较困难，是教学环节中的难点问题。我们从关系代数除法运算的定义出发，用整数除法对其进行类比；然后，用基本运算表示关系代数除法运算，剖析其运算本质；最后，引导学生操作SQL语句实现关系代数除法运算。教学实践表明，以具体实例为牵引，从概念到本质，再到实践的教学过程，形象直观地表达了关系代数除法运算，解决了其抽象定义难以被学生理解的问题，有助于学生对知识点的透彻理解，取得了较好的教学效果。

参考文献：

[1] 刘国燊. 数据库技术基础及应用[M]. 北京： 电子工业出版社， 2008： 55-66.

[2] 陆熊， 陈燕， 黄晓梅， 等. 关系代数中除法运算的教学探讨[J]. 现代计算机， 2011（5）： 42-44.

[3] 姚普选. 数据库系统： 基础、设计及应用[M]. 西安： 西安电子科技大学出版社， 2013： 40-45.

[4] 杨海鹏， 徐志英. 关系代数教学中除法运算的细节探讨[J]. 吉林工程技术师范学院学报， 2014（1）： 86-87.

[5] 肖海蓉. 关系代数中除法运算与SQL中带有exists子查询的对比教学[J]. 电脑学习， 2009（6）： 158-159.

（编辑：宋文婷）