基于BP神经网络的电力系统短期负荷预测

李咏馨，朱家明，吴梦晗，厉培培

（安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030）

科技与艺术设计

基于BP神经网络的电力系统短期负荷预测

李咏馨，朱家明，吴梦晗，厉培培

（安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030）

针对短期电力系统负荷预测问题，根据已知的地区1、2的电力负荷数据，结合图像对两地区负荷变化情况进行简要分析；通过建立电力负荷数据与各气象因素的回归关系，证明气象因素对负荷预测数据准确度和精度有影响；然后构建BP神经网络模型，得到负荷预测数据，并推断预测的准确度，对两地区整体负荷规律性的优劣做出合理地判断及评价.

多元线性回归；BP神经网络；SPSS；MATLAB

短期负荷预测是电力系统运行与分析的基础.当今社会，保障电力系统优化决策科学性的重要手段之一就是提高负荷预测精度.电力负荷的影响因素有很多，因此建立电力负荷数据与各气象因素的回归关系很有必要，同时笔者将构建BP神经网络模型，对负荷进行预测，并推断其准确度.

1 数据来源与模型假设

数据来自2016年电工杯数学建模比赛A题，已知两地区从2009年1月1日至2015年1月10日的电力负荷数据以及2012年1月1日至2015年1月17日的气象因素数据.

针对本题，我们做了以下假设：（1）假设电力负荷状况不受社会活动、节日类型、突发事件，如停电维修和拉闸限电等因素影响，仅考虑天气因素以及日、周周期变化的影响；（2）假设不考虑气象要素对负荷的积累效应和延时效应；（3）假设不考虑电价政策的改变.

2 对两地区负荷数据进行初步统计

2.1 研究思路

统计两地区全年电力负荷指标的分布情况，绘制2014年负荷持续曲线，分析两地区负荷变化的主要差异，并比较两地区的离散系数大小，预判预测准确程度.

2.2 研究方法

通过对相关附件中原始数据进行计算处理，分别得到地区1和地区2全年的日最高负荷、日最低负荷、日峰谷差、日负荷率四个指标的值，接着我们对求解所得数据进行绘图处理，得到如下图示：

分析得地区1和地区2均在初夏时间开始增加对用电的需求，日最高负荷、日最低负荷和日峰谷差均在盛夏时节达到高峰，并且用电量在短时期内呈周期性变化.从秋季开始降低了对电量的需求，尤其是在冬季结束之后，用电量达到了年度的最低点.结合每周的负荷数据分析得到如下结论，工作日与假日负荷曲线具有不同的特点，具体呈现在早晚高峰上，工作日人们在白天工作，因此早高峰值比晚高峰值大很多，而周末则与其不同；因为具有一样的性质，不同工作日的负荷曲线具有相似的形状，同理，具有相似的形状的还有每周周末假日的负荷曲线.地区1和地区2的日负荷率均在80%上下波动，其中在夏季的波动较大，其余时节波动较小.根据2014年地区1、2的用电负荷数据，运用MATLAB绘制得到图3.

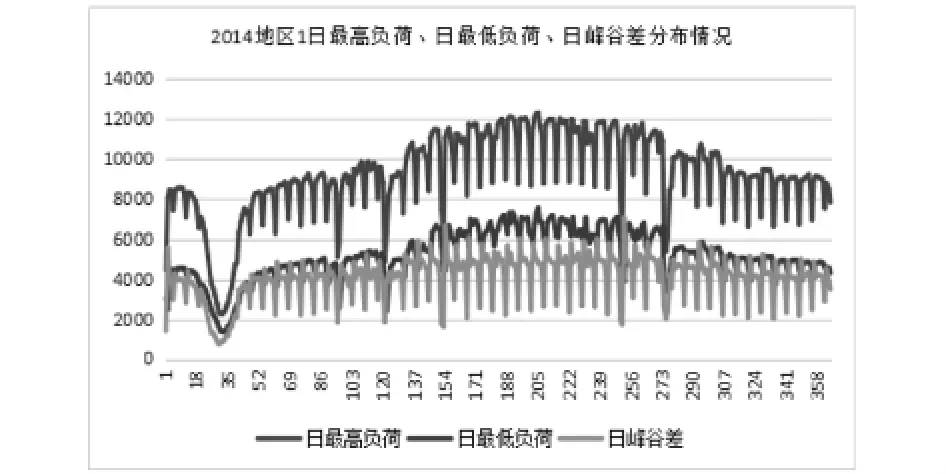
图1 地区1日最高负荷、日最低负荷、日峰谷差分布情况

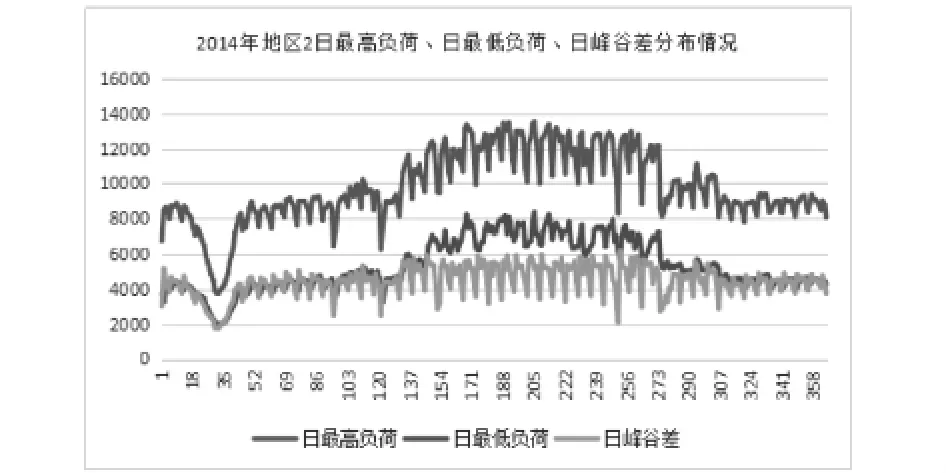
图2 地区2日最高负荷、日最低负荷、日峰谷差分布情况

主要差异：①地区1在夏季及前后用电量低于地区2，却在其他时间高于地区2；②地区1的日峰谷差均值小于地区2，但其波动幅度却明显大于地区2；③地区1常年用电负荷波动小于地区2；④地区1的日负荷率波动幅度明显高于地区2.⑤地区1的用电分布较为均衡，预判得到的均值也较地区2低.

图3 2014年地区1、2全年用电负荷持续曲线

2.3 结果分析

地区2的各数据的离散系数小，其离散程度也就较小，其均值代表性越大，结果越准确.离散系数反映单位均值上的离散程度，具有较大离散系数的总体其分布情况差异也大，分布情况的较大差异也致使预测误差增大，经计算得下表1.

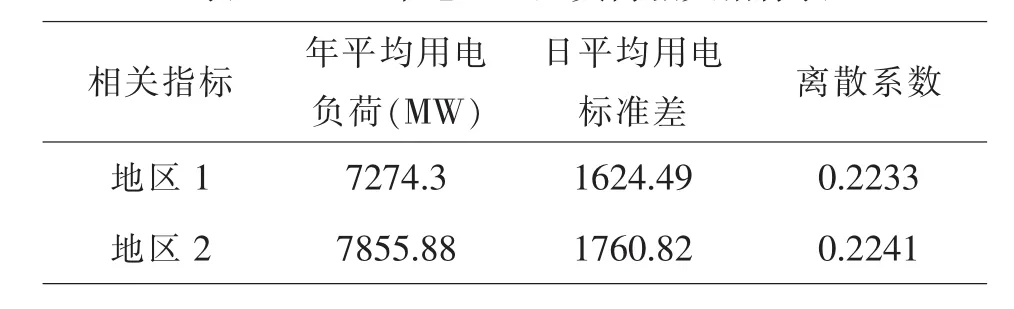
表1 2014年地区1、2负荷相关指标表

由于CV1＜CV2，故地区1平均数据的代表性越高，预测得到的结果误差越小.

3 基于多元线性回归的负荷预测的准备

3.1 研究思路

根据已知数据，我们要探究众多气象因素与负荷指标之间的关系，首先通过建立二者之间的线性回归方程，之后再分析哪一个气象因素能提高负荷预测精度.

3.2 研究方法

利用SPSS的多元线性回归中的逐步法，分析负荷与气象因子的依存关系.为了反映气象因子对一天日最高负荷、日最低负荷、日平均负荷的影响作用，分别采用地区1和地区2在2012年到2014年每天的日最高负荷Lmax、日最低负荷Lmin、日平均负荷Lave与气象因子（日最高温度Tmax、日最低温度Tmin、日平均温度Tavg、日相对湿度H以及日降雨量P）的逐步线性回归，结果见表2和表3.这里以地区1的数据为例进行解释说明.

①日最高负荷的线性回归方程

首先用SPSS日最高负荷对五个气候因素进行线性回归分析，得系数表.

易得该模型拟合度为0.396，由系数表t检验数据可知，最高温度和降雨量这两个指标没有通过t检验，很明显日最高负荷Lmax无法同时和5个气候因素建立多元线性回归关系.但可以看出日最高负荷Lmax与最低温度、平均温度、相对湿度存在回归关系，对自变量进行调整和剔除后，我们得以下结果.

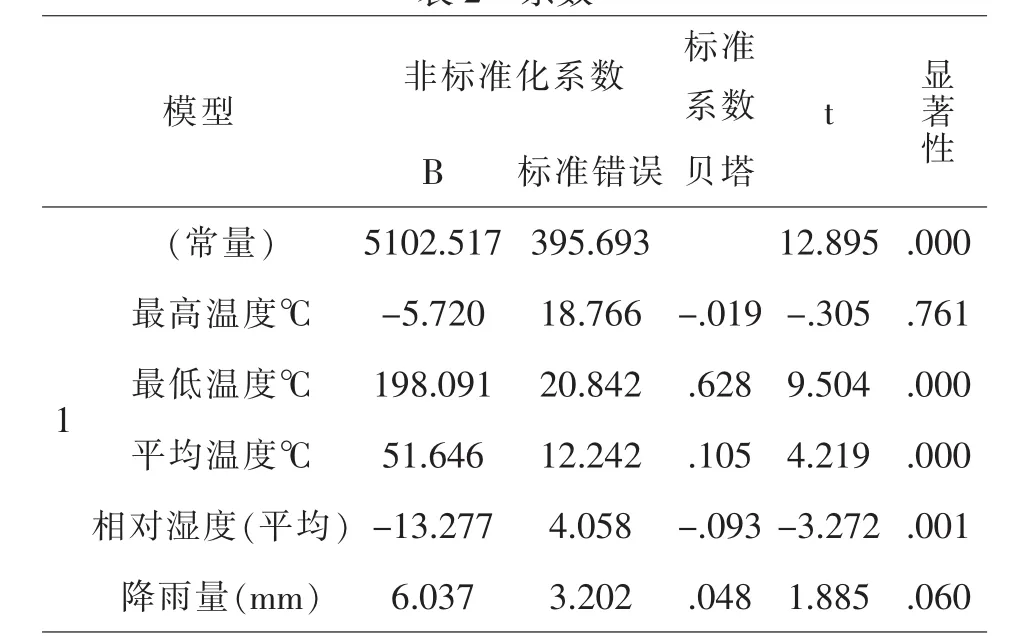
表2 系数a

表3 系数a

①地区1日最高负荷的线性回归方程

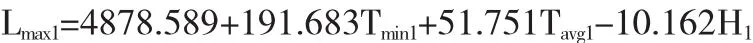
同理得：

②地区1日最低负荷的线性回归方程

③地区1日平均负荷的线性回归方程

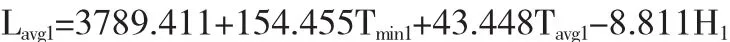
④地区2日最高负荷的线性回归方程

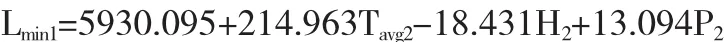
⑤地区2日最低负荷的线性回归方程

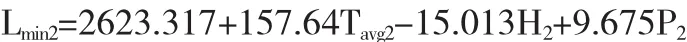
⑥地区2日平均负荷的线性回归方程

3.3 结果分析

我们发现，地区1的日最高负荷、日最低负荷、日平均负荷总是与最低温度、平均温度、相对湿度有关，地区2的日最高负荷、日最低负荷、日平均负荷总是与平均温度、相对湿度、降雨量有关.可以通过人体体感来解释变量与因变量之间的关系，温度、湿度、降雨量这些因素会影响我们的人体感受.当温度过高或过低，湿度过大或过小时，人体体感不适，可能会需要通过开空调、加湿器等行为来调节环境条件，缓解人体不适，从而就会影响每日多用电荷的多少.且在6组t检验中，地区1的t值最大的总是最低温度，其次是平均温度；地区2的t值最大的总是平均温度.因为每个地区的负荷特征的影响因素不同，我们将最低温度和平均温度统称为温度.因此，我们认为能提高负荷预测精度的因素为温度.

4 基于BP神经网络的短期负荷预测

4.1 研究思路

根据已知负荷数据，构建BP神经网络模型，经过MATLAB运算，得到未来7天、间隔为15min的96*7的负荷预测数据.我们可以对已知的数据做出预测值，计算得到预测结果的准确度.

4.2 研究方法

BP(Back-Propagation)神经网络即误差反传误差反向传播算法的学习过程，我们用图4来解释BP神经网络的传输模式，如图4，这是一个3层的前馈神经网络，其中第一层是输入层，第二层称为隐含层，第三层称为输出层.

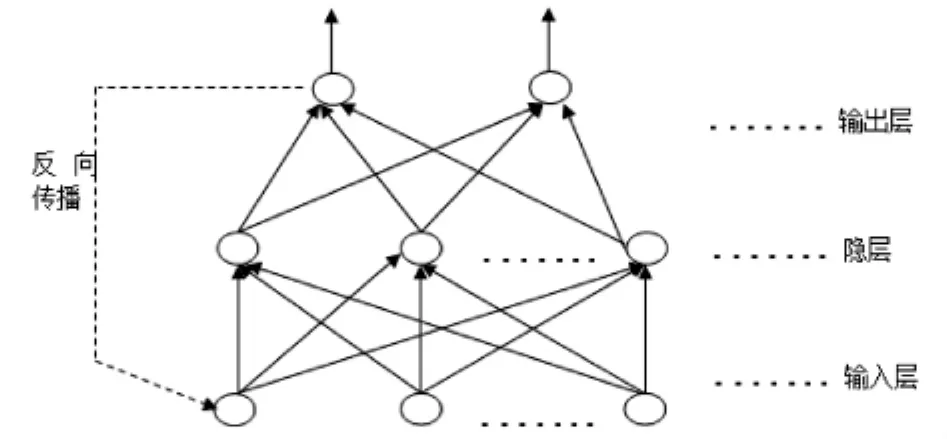
图4 前馈神经网络

为预测2015年1月11日至1月17日的负荷数据，我们主要选取了2015年1月4日至1月10日的负荷数据作为输入数据，进行BP神经网络预测.我们已经知道一周的每一天为不同类型，一天一共有96组负荷数据，用之进行预测.因此，输入变量与输出变量都96维的向量.

对输入和输出负荷数据进行归一化处理，根据公式：

X^为网络输入的归一化的数值，Xmin为最小值，Xmax为最大值.

在本系统的训练过程中，我们选取2015年1月4日到1月10日负荷值作为网络的训练样本，预测1月11日的电力负荷.模型的网络结构为“96-50-96”，其中，隐含层神经元个数为50.网络中间层的传输函数：S(sigmoid)形函数；输出层神经元传递函数：线性函数logsig.

在这里我们以地区一为例，仅列出部分训练代码进行说明：

训练次数设定为5000；训练目标定为0.01；学习速率定为0.1

根据MATLAB的运算结果，经过5000次训练后，网络误差达到要求，结果如图5所示.

下面我们需要进行测试来判断这个训练好的网络是否可以投入实际使用.这里的测试数据就是2015年1月10日的电力负荷来预测11日的用电负荷，以检验预测误差能否满足要求.代码如下：

%P_test为10日的电力负荷作为测试向量

图5 网络误差分析

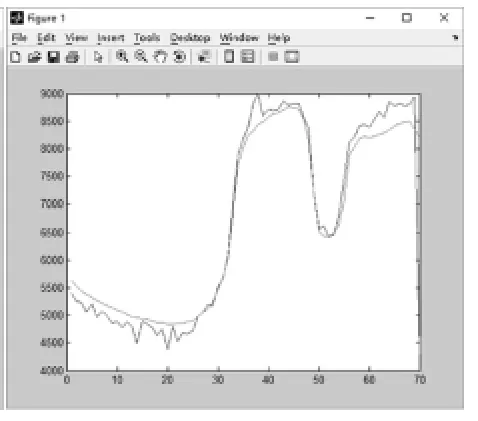
图6 负荷曲线拟合图

计算网络的输出，我们可以使用仿真函数sim来，计算结果经过反归一化处理后得到预测的11日的电力负荷值，同理，可以预测出两地区各自从11日至17日的负荷值，将所得10日的预测负荷值和实际电力负荷值相比较可得到网络的预测误差，将数据中的异常数据剔除之后计算得到地区1的平均误差为3.74%，地区2的平均误差为6.65%.同时用MATLAB作图绘制地区1的10日的预测数据和实际数据的曲线拟合图，见图6，利于直观地观察预测的准确性.

4.3 结果分析

从预测数据及图像可以看出，负荷预测基本上可以达到要求，但是，也有一些存在的问题.由求解结果可看出运用BP模型预测出的数据与实际数据相比误差率基本上处于3%～8%之间，但我们发现，当预测一整天的96个时点对应的数据时，对前七十多个时点的预测值比较接近实际数据，而后面二十多个数据则会出现相对较大的误差，所以准确度平均可达到72.92%左右，准确度较高.之后，我们又将温度、湿度等因素加入训练样本，来改进预测的结果，提高精确度.

5 结束语

使用SPSS进行多元回归分析，可快速清晰的得到检验结果，有利于确定气象特征因素；BP神经网络模型具有较强的非线性映射能力以及高度自学习和自适应的能力，有利于根据预测日前几日数据逐步推出预测日数据.

〔1〕杨桂元.数学建模[M].上海:上海财经大学出版社，2015.

〔2〕杨桂元，朱家明.数学建模竞赛优秀论文评析[M].合肥:中国科学技术大学出版社，2013.

〔3〕姜启源，谢金星，叶俊.数学模型（第四版）[M].北京:高等教育出版社，2011.

〔4〕宋亮.基于BP神经网络的短期电力负荷预测[D].西安工业大学，2011.55～57.

〔5〕万志宏.基于时间序列的电力系统短期负荷预测研究[D].华南理工大学，2012.67～69.

〔6〕徐东升，杨巍，魏哲，刘国兴.基于SPSS的短期负荷特性分析及其预测研究 [J].电力系统保护与控制，2009(21): 22～25.

〔7〕王琪，张明理.基于概率统计的负荷规律性评价方法的研究[J].东北电力技术，2008(02):45～50.

TM715

A

1673-260X（2017）08-0022-03

2017-05-19

国家自然科学基金项目：3-流猜想，Fulkerson-覆盖及相关问题（11601001）；国家级大学生创新训练项目：去产能和调转促背景下旅游产业对安徽省转型的动力贡献分析--基于DEA方法（201610378172）；安徽财经大学教研项目（acjyzd201429）