结合地震易损性分析的桥梁地震损伤识别
单德山, 周筱航, 杨景超, 李 乔
(西南交通大学 土木工程学院,成都 610031)
结合地震易损性分析的桥梁地震损伤识别
单德山, 周筱航, 杨景超, 李 乔
(西南交通大学 土木工程学院,成都 610031)
目前在使用模式识别理论进行复杂桥梁地震损伤识别时仍存在许多困难,如损伤模式不易确定、损伤指标难以提取和无法构建足够数量损伤样本等。针对上述问题,提出了一种基于地震易损性分析的桥梁地震损伤模式识别新方法。将地震激励分为主震和余震两类。使用主震对桥梁进行地震易损性分析以确定其在地震激励下可能发生的损伤情形,进而确定地震损伤模式和有策略地布置传感器。使用余震激励已损伤桥梁获得其动力响应信息,以构建足够数量的数据样本。使用希尔伯特黄变换(Hilbert-Huang Transform, HHT)对结构响应数据进行处理,提取对损伤敏感的指标(Damage Index,DI)。采用模式识别理论建立DI与损伤模式之间的对应关系,实现对桥梁地震损伤模式的识别。将所提方法应用于连续刚构桥的地震损伤识别,结果表明该方法可准确识别桥梁地震损伤,且算法具有较强的抗噪声干扰能力。
桥梁;地震易损性分析;地震损伤;模式识别;损伤指标;
结构地震损伤识别的目的是为了在震中或震后及时地对结构损伤的位置和程度进行识别,进而根据损伤识别结果制定相应的结构修复方案[1]。传统的结构地震损伤识别方法主要建立在优化算法基础上,但此类方法存在着识别精度低、易陷入局部最小解等缺点[2-5],为解决上述问题,Farrar等[6]提出将结构损伤识别视为模式识别问题进行求解。
众多学者对基于模式识别理论的结构地震损伤识别方法展开了研究。Andreadis等[7]以地面峰值加速度(Peak Ground Acceleration, PGA)、地面峰值速度(Peak Ground Velocity, PGV)、强震持时(Strong Motion Duration, SMD)、有效峰值加速度(Effective Peak Acceleration, EPA)等统计特征作为损伤指标,使用模糊理论对地震波进行分类,并依据地震波所属模式来评估结构在此激励下可能发生的损伤。De Lautour等[8]用自回归模型拟合结构在地震激励下的加速度响应信号,将拟合结果作为损伤指标对人工神经网络(Artificial Neural Network, ANN)进行训练,成功对框架结构的损伤进行了识别。Dong等[9]用希尔伯特黄变换(Hilbert-Huang Transform, HHT)方法提取结构的自振频率,并以高阶频率的能量变化情况作为损伤指标,结合向量自回归模型对框架结构的地震损伤模式进行了识别。Vafaei等[10]用小波变换对机场控制塔在地震激励下的加速度响应信号进行处理,根据小波变换系数的变化情况识别了控制塔3种不同的地震损伤模式。
随着统计推断理论的发展及Vapnik-Chervonenkis理论的建立,支持向量机(Support Vector Machine,SVM)作为一种新的模式识别方法逐渐被用于结构损伤识别研究[11]。Farooq等[12]以结构应变值作为损伤指标,分别使用ANN和SVM方法对板结构的损伤进行了识别,识别结果表明SVM比ANN具有更高的识别精度。Bao等[13]以结构自振频率作为损伤指标,使用SVM对桥墩损伤进行了识别。Mechbal等[14]根据声波在结构中传导特性的变化,使用SVM方法识别了组合板结构中的损伤。Ren等[15]以挠度作为损伤指标,用SVM识别了钢桁架结构的损伤情况,但以挠度作为损伤指标时算法的抗噪声干扰能力不强。单德山等[16]对SVM在结构损伤识别领域中的应用情况做了详细论述,并讨论了SVM在时域及时频域内训练参数的选取问题。
目前SVM多被应用于识别框架或板等简单结构的损伤,在识别复杂结构损伤时,则需要提取可准确描述复杂损伤模式的特征指标。另外,在现有研究中结构的损伤模式大多由人为指定,这种方法并不适用于确定复杂结构的地震损伤模式。桥梁结构在地震作用下可能发生多处不同程度的损伤,其损伤模式较为复杂;同时地震为短时激励,在地震过程中可获取的结构响应信息较少。上述特性使得在应用SVM方法识别桥梁地震损伤时存在着损伤模式不易确定、难以提取有效的损伤指标以及无法获取足够数量损伤样本等问题。
为了克服上述问题,本文在既有研究的基础上[17-19],提出了一种基于地震易损性分析的桥梁地震损伤模式识别方法,并以非规则高墩大跨连续刚构桥为研究对象,对所提方法进行了验证。
1 识别理论和方法
由以往工程经验可知,在地震的主震发生后,一般还将发生多次余震:汶川地震后发生余震1万余次、芦山地震后发生余震4 000余次。若通过余震激励下结构的响应信号来获取结构损伤信息,则可有效解决桥梁地震损伤识别过程中难以获得足够数据样本的问题,因此在本研究中考虑将地震分为主、余震两类,使用主震诱发桥梁地震损伤,使用余震获取桥梁损伤状态信息。
首先,使用主震对桥梁结构进行地震易损性分析,根据桥梁地震易损性分析结果确定贴合实际的地震损伤模式,同时对传感器进行有策略的布置。然后,使用多条不同形式的余震激励受损桥梁以获得结构响应。使用HHT对桥梁的输入、输出信号进行处理,提取可准确描述桥梁损伤状态的损伤指标(Damage Index, DI),并构建桥梁地震损伤模式样本库。最后,使用SVM建立损伤指标DI与损伤模式之间的对应关系,对桥梁的地震损伤进行识别。桥梁地震损伤模式识别流程如图1所示。

图1 地震损伤模式识别流程Fig.1 Process ofseismic damage pattern recognition
1.1 地震易损性分析
结构地震易损性分析通过计算在一定强度地震作用下结构达到或超过某一极限状态的概率,从宏观角度描述了地震作用强度与结构发生破坏之间的概率关系[20],归纳如式(1)所示。
FR(x)=P[D≥C|IM=x]
(1)
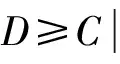
1.2 传感器布置
根据桥梁地震易损性分析结果中发生地震损伤单元的最大分布范围,确定出桥梁结构的地震易损区域。为了使用较少的传感器获得可完整描述桥梁损伤状态的结构响应数据,同时保护传感器在地震过程中免受损坏,考虑将传感器布置在桥梁易损区域的边界处。
1.3 损伤模式及损伤样本确定
在现有的结构损伤识别研究中,损伤的模拟方法大多为人为指定结构某处发生某种程度的损伤。在地震激励下,桥梁发生损伤的机理极为复杂[21],若不考虑桥梁结构特性和地震动特性,仅通过人为指定损伤,将导致地震损伤模拟结果背离工程实际。为了真实模拟桥梁在地震激励下可能发生的损伤情形,首先对地震易损性分析结果中出现的损伤状态进行分类,即确定地震损伤模式,进而将损伤模型归入相应损伤模式,确定桥梁地震损伤样本。
随着地震激励强度的增加,实际发生损伤的易损区域也逐渐增多。在本研究中,根据桥梁各易损区域是否发生损伤确定不同的地震损伤模式,该方法有利于使用较少的损伤模式概括桥梁在地震作用下发生损伤的总体情况。将损伤模型归入相应损伤模式,通过弯矩-曲率比值查看损伤单元的刚度折减情况,获得损伤样本的损伤程度信息。
1.4 损伤指标提取
损伤指标的有效性直接影响损伤识别结果的准确性,提取合适的损伤指标是损伤识别研究中的关键问题。在本研究中,使用HHT对结构输入、输出信号进行处理,构建对结构局部损伤敏感的指标DI。
HHT是一种适用于处理非平稳、非线性数据的自适应时频域信号处理方法,广泛应用于地震动数据处理领域[22-23]。信号经HHT处理后得到Hilbert谱函数
(2)
将Hilbert谱函数对时间积分,得到描述振动能量在频率域内分布情况的Hilbert边际谱函数
h(ω)=∫H(ω,t)dt
(3)
Hilbert边际谱函数虽包含结构的损伤信息,但以Hilbert边际谱函数作为损伤指标不能有效区分结构的损伤状态,需对其作进一步的变换,将地震输入与结构输出的Hilbert边际谱函数进行比值,得到Hilbert边际谱传递函数
(4)
Hilbert边际谱传递函数为曲线函数,以其作为损伤指标存在数据量过大的问题。因此,对Hilbert边际谱传递函数在频率域内积分,将积分值定义为损伤指标DI
DI=∫T(ω)dω
(5)
1.5 模式识别方法
在本研究中,采用SVM作为模式识别算法,其可自动确定节点数目和节点权重,避免了过学习、欠学习和局部极小点等问题,是一种具有泛化性能好、全局最优和稀疏解等优点的模式识别方法[24-25]。
SVM求解不同模式的最优分类面拟合函数如式(6)所示
(6)

2 桥梁地震损伤识别算例
为详细论述本文所提桥梁地震损伤识别方法的实现过程及有效性,以非规则高墩大跨连续刚构桥为研究对象,对其进行地震损伤模式识别。
2.1 工程概况
连续刚构桥全长650 m,桥跨布置为80 m+130 m+2 m×170 m+100 m;4个桥墩高度分别为26.9 m、123.54 m、91.63 m和80.14 m;主梁为箱型梁,材料为C50混凝土;桥墩为空心薄壁墩,材料为C40混凝土;桥台及1#桥墩上安装有双向活动支座,其余桥墩与主梁固结。连续刚构桥总体布置情况如图2所示。
对于非规则高墩大跨连续刚构桥来说,地震作用下桥墩更易出现损伤,本文主要针对桥墩开展地震损伤识别算法研究,同时为降低分析难度,只考虑顺桥向的地震激励作用。
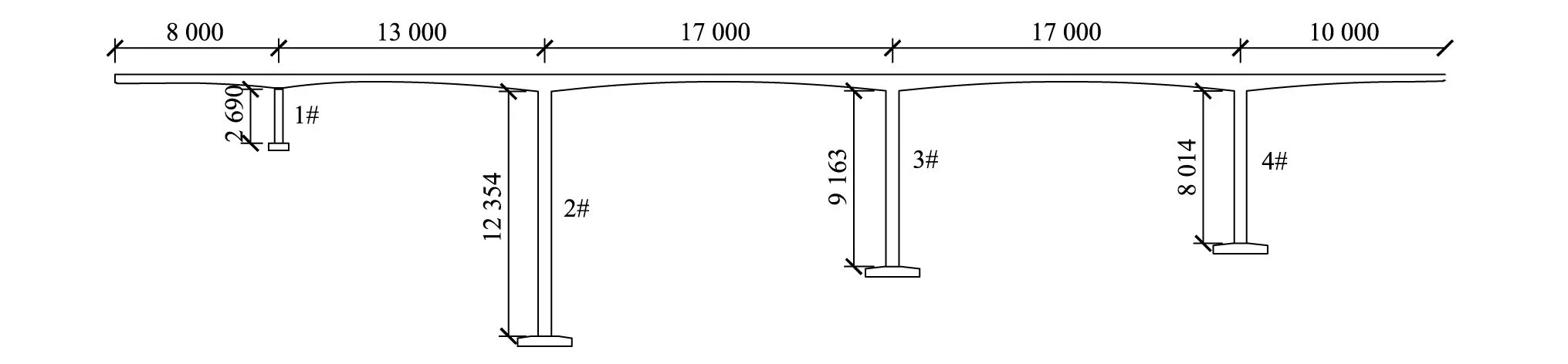
图2 桥梁总体布置图(单位:cm)Fig.2 General arrangement of the bridge(unit:cm)
2.2 地震易损性分析
使用OpenSEES建立连续刚构桥的数值模型,采用弹性梁柱单元(Elastic Beam-Column Elements,EBCE)模拟主梁,采用非线性梁柱单元(Nonlinear Beam-Column Elements,NBCE)模拟桥墩,采用零长度单元(Zero-Length Elements,ZLE)模拟双向活动支座。
选取加速度反应谱波形、有效持时差异较大的实测地震动记录以考虑地震动的离散性,共选出16条地震动记录,如表1所示。分别将16条地震波的PGA标准化到0.1~1.5g,步长为0.1g,共得到240条地震波以用于地震易损性分析。
考虑到较高的钢筋混凝土墩柱在地震作用下主要发生弯曲破坏[26],本文以曲率作为指标进行墩身高度方向的参数包络分析,得到各桥墩的曲率包络线如图3所示。由图3可以看出,1#桥墩底部曲率较大,但曲率数值总体偏小,2#~4#桥墩的顶部和底部曲率较大,可知在顺桥向地震动作用下,1#墩不易损伤,2#~4#墩的顶部和底部容易发生损伤。

表1 实测地震动记录
为了定量描述在不同PGA地震动作用下各桥墩发生不同程度地震损伤的可能性,引入适用于较高墩柱的基于曲率延性比的损伤程度判据,如表2所示。在表2中,φ1为墩底纵向钢筋首次屈服时的曲率;φ2为等效屈服曲率;φ3为截面边缘钢筋混凝土压应变达到0.002或0.004的曲率(当墩底存在纵筋搭接时取0.002,否则取0.004);φ4为极限曲率。φ1~φ4参照Caltrans[27]提出的方法进行计算,具体取值如表3所示。根据桥墩各截面在地震作用下达到的最大曲率值与表3中的曲率限值对比,得到桥墩在不同PGA地震作用下发生不同程度地震损伤的概率,即桥墩地震易损性曲线,如图4所示。

表2 基于曲率的损伤程度判据

表3 桥墩临界曲率值

图3 桥墩曲率包络Fig.3 Curvatureenvelope of piers

图4 桥墩发生地震损伤概率Fig.4 Damage probability of piers
2.3 传感器布置
通过查看地震易损性分析结果中桥墩可能出现地震损伤的单元的最大分布范围,确定出各桥墩的易损区域。根据各桥墩易损区域分布情况,对传感器进行有策略的布置。为了使传感器测试数据尽可能多的包含结构损伤状态信息,同时保证传感器在地震过程中不被损坏,选定各桥墩易损区域边界处作为加速度传感器的安装点位。各桥墩的易损区域分布及传感器布置情况如图5所示,图中填充区域为易损区域,○指向位置为加速度传感器布置点位,①中数字为传感器编号。
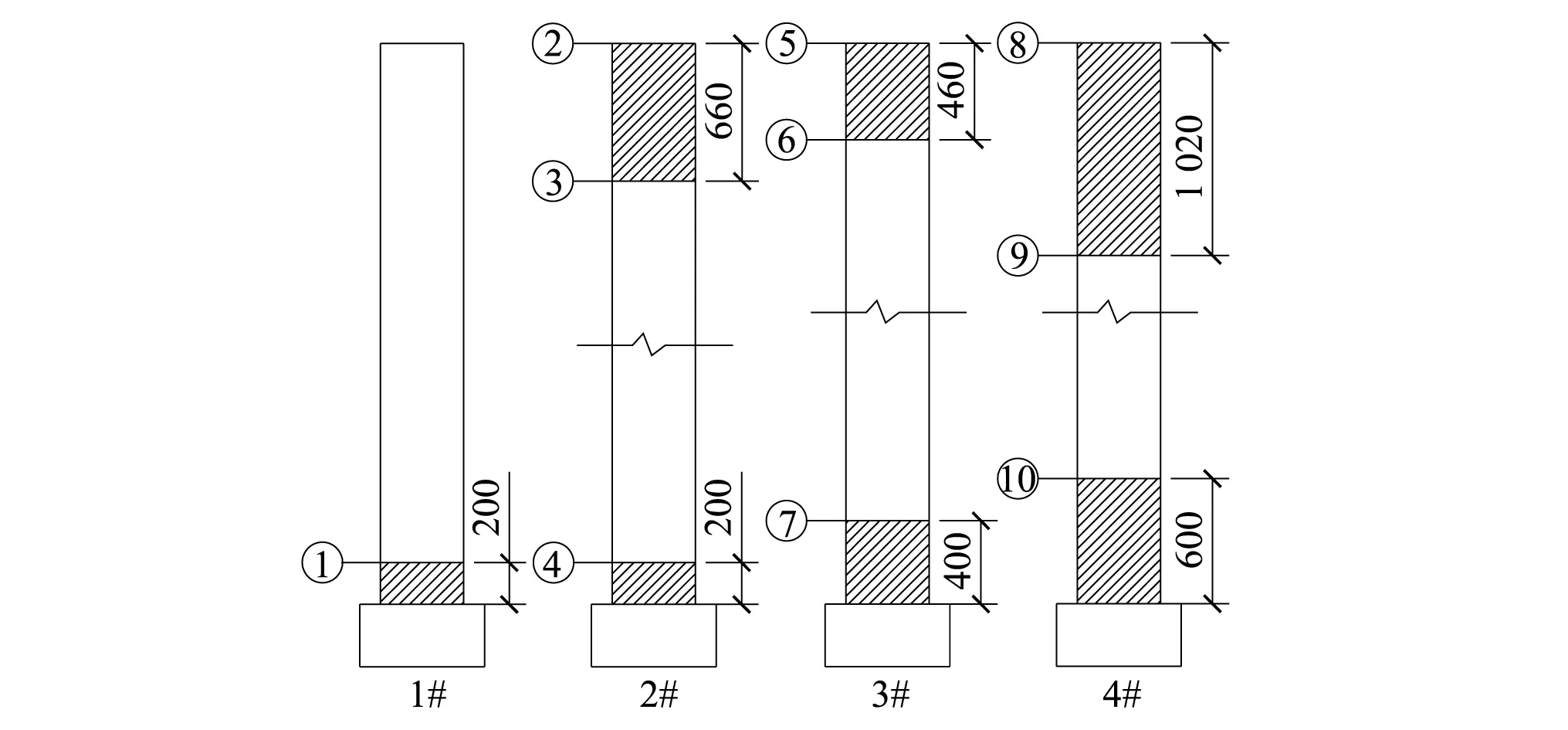
图5 易损区域分布及传感器布置(单位:cm)Fig.5 Vulnerable zone distribution and sensor arrangement(unit:cm)
2.4 损伤模式及损伤样本确定
考虑到《建筑抗震设计规范》中规定的设计基本地震加速度值均在0.5g以下,为讨论更符合工程实际的情况,本文根据地震激励PGA在0.5g及以下时各桥墩的损伤状态进行损伤模式的划分和损伤样本的构建。根据各桥墩的易损区域内是否出现地震损伤,将桥梁地震损伤分为不同模式,损伤模式的定义方法如表4所示。通过提取刚构桥地震易损性分析过程中易损区域内各单元的弯矩-曲率比值,得到桥梁损伤模型各单元的刚度折减情况。按照表4定义的损伤模式对发生不同程度损伤的桥梁模型进行归类,进而确定了各损伤模式对应的刚度折减范围,同时从各损伤模式中分别选取了1个刚度折减程度偏中的损伤模型作为待识别样本,共计3个。确定出的各损伤模式单元刚度折减范围及待识别样本的单元刚度折减程度列于表5。

表4 损伤模式
2.5 损伤指标提取
根据《公路桥梁抗震设计细则(JTJ/TB 02-01—2008)》中4种场地类型设计反应谱的规定,采用数值方法生成PGA不大于0.05g的4种场地类型余震波,共计100条。使用余震波激励已损伤桥梁模型,获得损伤模型的结构响应输出信号,按照式(1)和式(2)对桥梁结构的输入、输出信号进行处理,得到Hilbert边际谱函数。完好模型和损伤模型的Hilbert边际谱函数如图6所示,可见Hilbert边际谱函数不能有效区分结构的不同状态。使用式(4)对Hilbert边际谱函数进行处理,得到Hilbert边际谱传递函数如图7所示,可以看出Hilbert边际谱传递函数能反映结构不同的损伤状态,但使用完整曲线作为损伤指标存在着数据量过大的问题。为加快运算效率,使用式(5)对Hilbert边际谱传递函数在0~100 Hz的频域内积分,得到损伤指标DI。图8中给出了在4种场地类型余震波激励下4#桥墩分别处于完好、轻微损伤、严重损伤状态时,⑧传感器获取的损伤指标DI。

表5 桥墩地震损伤程度
2.6 损伤识别
在单次余震激励下1个加速度传感器采集的数据可提取1个损伤指标DI。如图5所示,连续刚构桥上共布置有10个加速度传感器,单次余震激励下则可获得10个损伤指标DI。分别将10个DI和相应的损伤模式作为模式分类算法的输入、输出参数,形成一个样本。
桥梁地震损伤的模式识别算法分为两种情况进行。过程一:检验算法在余震场地类型未知、损伤模式已知情况下的识别能力;过程二:检验算法在余震场地类型已知、损伤模式未知情况下的识别能力。最后,分别向过程一、过程二中添加噪声,检验算法的抗噪声干扰能力。
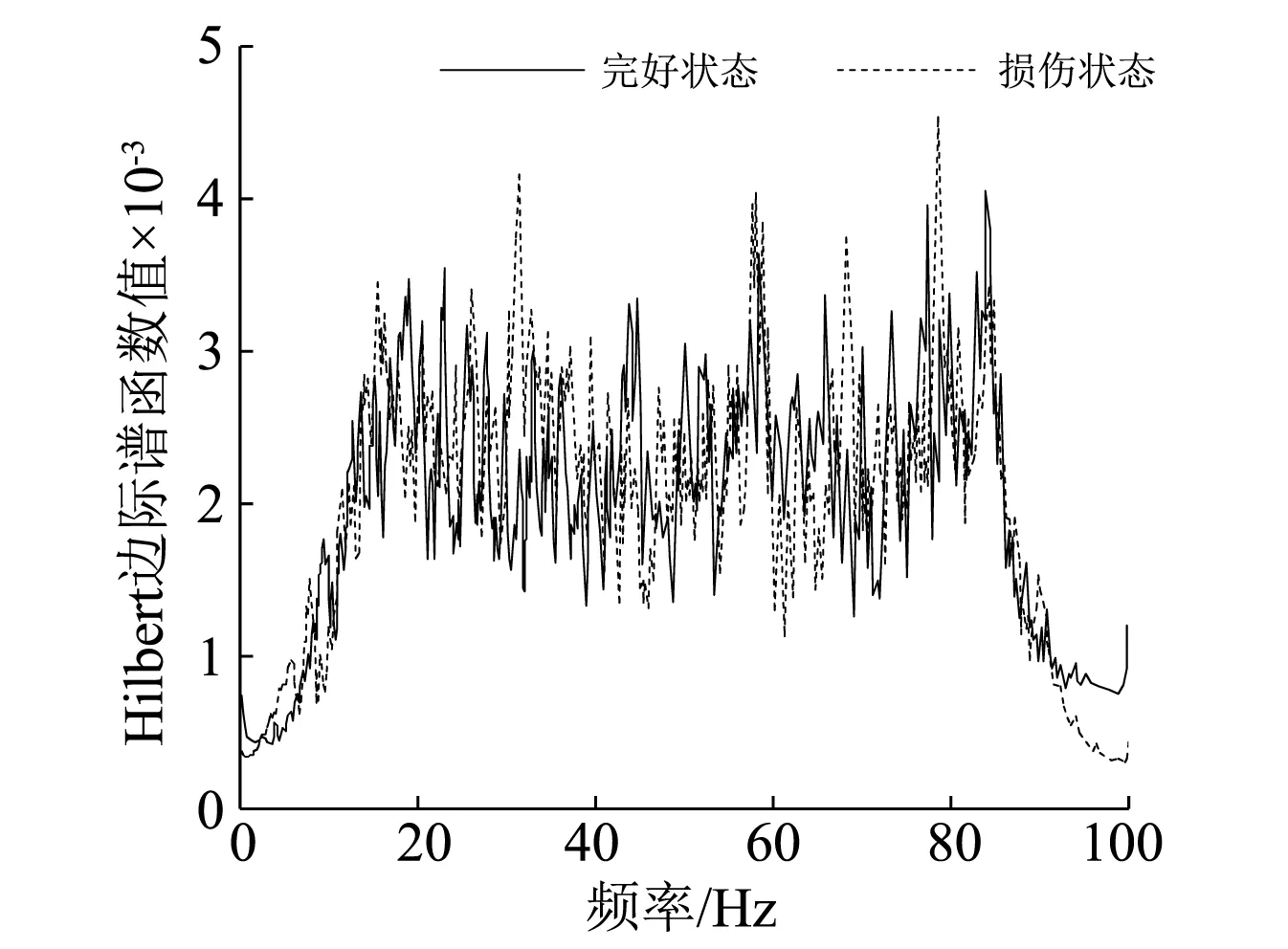
图6 Hilbert边际谱Fig.6 Hilbert marginal spectrum
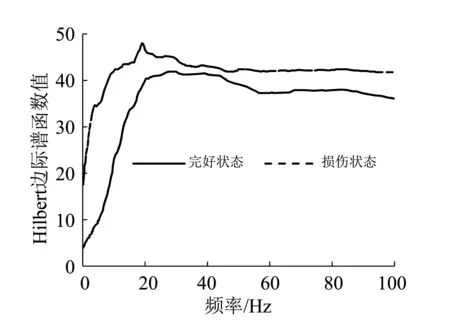
图7 Hilbert边际谱传递函数Fig.7 Hilbert marginal spectrum transfer function

图8 损伤指标DIFig.8 Damage index(DI)
(1)过程一:从表5定义的3种损伤模式中,随机各选取1个损伤模型,共计3个。随机抽取100条余震波中的80条余震波激励损伤模型,得到240个训练样本。使用余下的20条余震波激励损伤模型,得到60个测试样本。使用训练样本及测试样本对算法进行检验。
(2)过程二:考虑到实际桥梁工程受到的余震激励与桥址处的场地类型有关,故本阶段中只选取特定场地类型的余震波作为激励。根据表5中所示的桥墩地震损伤程度变化范围,分别从3类损伤模式中选取邻近损伤程度轻微和严重的损伤模型各5个,共计30个损伤模型。选取20条二类场地余震波激励损伤模型,得到600个训练样本。使用相同的20条余震波激励表5中的3个待识别损伤模型,得到60个测试样本。使用训练样本及测试样本对算法进行检验。
(3)抗噪性检验:向数据中分别添加5%~30%的白噪声,重复地震损伤识别过程一及过程二。
2.7 识别结果与讨论
表6中给出了在不同噪声水平干扰下桥梁地震损伤识别两个过程的识别结果。

表6 地震损伤模式识别结果
在过程一中,待识别的损伤样本已参与训练,影响识别结果的主要因素为余震激励场地类型离散性和噪声;在过程二中,余震激励的场地类型已知,影响识别结果的主要因素为待识别损伤样本离散性和噪声。
在无噪声干扰情况下,两过程均可实现对桥梁地震损伤模式的准确识别,且过程二识别结果具有更高的正确率。在有噪声干扰情况下,当噪声水平在10%以下时,两过程的识别结果均不受噪声影响;随着噪声水平的增强,两过程识别结果的正确率逐渐下降,但过程二识别结果正确率在噪声水平大于20%时才出现降低;当噪声水平进一步增大到30%时,过程一识别结果正确率下降较为明显,过程二识别结果仍保证了较高的正确率。另外,在两个过程中,随着桥梁损伤程度的增加,识别结果正确率均逐渐升高。
术后的随访应该是长期和终身的,一般建议是在前2年每3个月随访1次,每6个月随访2~5年,随后每年随访1次。随访内容应包括经阴道超声检查和CA125水平,不推荐常规行CT或MRI检查,但当CA125显著升高时应进一步行CT检查。如未完成生育的BOTs患者行保守手术后再复发仍可进行保留生育功能的手术,如无生育要求,可行双侧附件切除术。若为卵巢外复发,最好行肿瘤细胞减灭术,最重要的预后因素是残余肿瘤的存在,因此尽可能去除肿瘤组织是非常重要的。
由识别结果可以看出,本文所提出的桥梁地震损伤模式识别方法具有较高的识别正确率及抗噪声干扰能力;且在余震场地类型已知,即更符合工程实际的情况下,方法的识别正确率得到显著提高。
3 结 论
本文提出了一种基于地震易损性分析的复杂桥梁地震损伤模式识别方法,将所提方法应用于连续刚构桥的地震损伤识别,获得如下主要结论:
(1)使用主震对桥梁进行地震易损性分析,可确定贴合工程实际的桥梁地震损伤模式,同时为传感器的优化布置提供依据。
(2)使用余震获取桥梁动力响应信息,可有效扩充富含桥梁损伤状态信息的数据样本容量。
(3)基于HHT方法构建了表达形式简洁且对桥梁地震损伤敏感的损伤指标。
(4)数值算例结果表明,所提方法具有较高的识别精度和较强的抗噪声干扰能力,且在余震场地类型确定时方法识别精度得到显著提高。
[ 1 ] 单德山,李乔,付春雨,等.智能桥梁健康监测与损伤评估[M]. 北京:人民交通出版社, 2010.
[ 2 ] FRISWELL M I, PENNY J E T, GARVEY S D. A combined genetic and eigensensitivity algorithm for the location of damage in structures[J]. Computers & Structures, 1998, 69(5): 547-556.
[ 3 ] FARRAR C R, JAUREGUI D A. Comparative study of damage identification algorithms applied to a bridge: I. Experiment[J]. Smart Materials and Structures, 1998, 7(5): 704-712.
[ 4 ] FARRAR C R, HEMEZ F M, SHUNK D D, et al. A review of structural health monitoring literature: 1996-2001[M]. Los Alamos: Los Alamos National Laboratory, 2004.
[ 5 ] FAN Wei, QIAO Pizhong. Vibration-based damage identification methods: a review and comparative study[J]. Structural Health Monitoring, 2011, 10(1): 83-111.
[ 6 ] FARRAR C R, WORDEN K. Structural health monitoring[M]. John Wiley & Sons, 2013.
[ 7 ] ANDREADIS I, TSIFTZIS I, ELENAS A. Intelligent seismic acceleration signal processing for damage classification in buildings[J]. IEEE Transactions on Instrumentation and Measurement, 2007, 56(5): 1555-1564.
[ 8 ] DE LAUTOUR O R, OMENZETTER P. Damage classification and estimation in experimental structures using time series analysis and pattern recognition[J]. Mechanical Systems and Signal Processing, 2010, 24(5): 1556-1569.
[ 9 ] DONG Yinfeng, LI Yingmin, LAI Ming. Structural damage detection using empirical-mode decomposition and vector autoregressive moving average model[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(3): 133-145.
[10] VAFAEI M, ADNAN A. Seismic damage detection of tall airport traffic control towers using wavelet analysis[J]. Structure and Infrastructure Engineering, 2014, 10(1): 106-127.
[11] VAPNIK V N. Statistical learning theory[M]. New York: Wiley, 1998.
[12] FAROOQ M, ZHENG H, NAGABHUSHANA A, et al. Damage detection and identification in smart structures using SVM and ANN[C]∥ Smart Structures and Materials+ Nondestructive Evaluation and Health Monitoring, International Society for Optics and Photonics. [S.l.]:SPIE, 2012.
[13] BAO Yaojin, SONG Chenjin, WANG Wensi, et al. Damage detection of bridge structure based on SVM[J]. Mathematical Problems in Engineering, 2013(6):1-7.
[14] MECHBALN, URIBE J S, REBILLAT M. A probabilistic multi-class classifier for structural health monitoring[J]. Mechanical Systems and Signal Processing, 2015, 60: 106-123.
[15] REN Jianying, SU Mubiao, ZENG Qingyuan. Damage identification of railway simply supported steel truss bridge based on support vector machine[J]. Journal of Applied Sciences, 2013, 13(17): 3589-3593.
[16] 单德山, 付春雨, 李乔. 桥梁结构损伤诊断的统计学习理论[M]. 北京:科学出版社, 2014.
[17] 黄振兴. 震后桥梁结构时频域损伤诊断研究[D].成都:西南交通大学,2012.
[18] 杨景超. 基于HHT和SVM的震后桥梁结构损伤诊断研究[D].成都:西南交通大学,2014.
[19] 张少雄. 高墩桥梁地震易损性分析研究[D].成都:西南交通大学,2014.
[20] 吴巧云,朱宏平,樊剑. 基于性能的钢筋混凝土框架结构地震易损性分析[J]. 工程力学,2012,29(9):117-124. WU Qiaoyun, ZHU Hongping, FAN Jian. Performance-based seismic fragility analysis of RC frame structures[J]. Engineering Mechanics, 2012, 29(9):117-124.
[21] 徐艳,段昕智,李建中.强震作用下斜拉桥纵桥向非线性地震反应分析[J].华南理工大学学报(自然科学版),2012, 40(6): 132-138. XU Yan, DUAN Xinzhi, LI Jianzhong. Analysis of nonlinear seismic response of cable-stayed bridge subjected to longitudinal strong ground motions[J]. Journal of South China University of Technology(Natural Science), 2012, 40(6): 132-138.
[22] HUANG N E, CHERN C C, HUANG K, et al. A new spectral representation of earthquake data: Hilbert spectral analysis of station TCU129, Chi-Chi, Taiwan, 21 September 1999[J]. Bulletin of the Seismological Society of America, 2001, 91(5): 1310-1338.
[23] LOH C H, WU T C, HUANG N E. Application of the empirical mode decomposition-Hilbert spectrum method to identify near-fault ground-motion characteristics and structural responses[J]. Bulletin of the Seismological Society of America, 2001, 91(5): 1339-1357.
[24] CHERKASSKY V, MA Y. Practical selection of SVM parameters and noise estimation for SVM regression[J]. Neural Networks, 2004, 17(1): 113-126.
[25] VAPNIK V. The nature of statistical learning theory[M]. Springe: Springer Science & Business Media, 2000.
[26] HWANG H, JERNIGAN J B, LIN Y W. Evaluation of seismic damage to memphis bridges and highway systems[J]. Journal of Bridge Engineering, 2000, 5(4): 322-330.
[27] CALTRANS. Seismic design criteria version 1.2[M]. California: California Department of Transportation, 2001.
Bridge seismic damage identification based on seismic fragility analysis
SHAN Deshan, ZHOU Xiaohang, YANG Jingchao, LI Qiao
(School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)
There are still many difficulties in applying the pattern recognition theory to complex bridge seismic damage identification, for example, it is not easy to determine damage patterns, and difficult to extract the damage index, and even it is a big challenge to obtain sufficient damage samples. To counter the mentioned problems, a novel bridge seismic damage pattern recognition method based on seismic fragility analysis was proposed. First, seismic excitations were classified into main-shocks and after-shocks. Main-shocks were used to carry out the bridge seismic fragility analysis in order to obtain the potential damage of the bridge, and as a consequent the layout of the sensors and the patterns of seismic damage were determined strategically. After-shocks were used to excite the damaged bridges to obtain their structural responses, and hence the sufficient data samples were acquired. Then, Hilbert-Huang Transform (HHT) was adopted to deal with the structural response data to extract the Damage Index (DI), which was sensitive to structural damage. Finally, the pattern recognition theory was applied to map the relationships between DI and the damage patterns, and the bridge seismic damage identification was achieved. The proposed method was adopted to identify the seismic damage of a continuous rigid frame girder bridge. The results show that the method can identify the bridge seismic damage patterns precisely and the noise immunity of the method is favorable.
bridge; seismic fragility analysis; seismic damage; pattern recognition; damage index
国家重点基础研究发展计划(2013CB036300);国家重点研发计划(2016YFC0802202);国家自然科学基金(51678489)
2016-07-29 修改稿收到日期: 2016-11-11
单德山 男,博士,教授,1969年生
周筱航 男,博士生,1989年生
U446
A
10.13465/j.cnki.jvs.2017.16.030

