离心压缩机叶轮主动再制造设计和时机调控方法
宋守许 卜 建 柯庆镝
合肥工业大学机械工程学院,合肥,230009
离心压缩机叶轮主动再制造设计和时机调控方法
宋守许 卜 建 柯庆镝
合肥工业大学机械工程学院,合肥,230009
针对目前再制造中零部件经常出现的“滞后再制造”或“提前再制造”问题,提出了离心压缩机叶轮主动再制造设计和时机调控方法。选取关键零部件特征结构,结合疲劳寿命理论和叶轮设计基础,建立结构与服役性能的映射模型,实现关键零部件的主动再制造设计。通过优化特征结构参数,改变零部件服役寿命和再制造临界点,并与产品综合性能劣化拐点相匹配,完成零部件主动再制造时机调控。以PCL8L型叶轮为例,基于构建的叶轮特征结构(出口安放角、入口安放角和后缘厚度)与寿命之间的量化关系模型,在当前定期维护需求下,通过理论计算和仿真分析,验证了主动再制造设计和时机调控方法的可行性。
主动再制造;离心压缩机;特征结构;时机调控
0 引言
离心压缩机是技术密集典型化的机电产品,广泛应用于石油、化工、电力和能源等国民经济支柱产业,随着国家可持续发展重大战略的推进,离心压缩机的再制造研究也愈发重要。而叶轮又是离心压缩机等大型旋转机械的主要承力和做功部件,其性能直接影响整个压缩机组运行的安全性和可靠性[1]。由于叶轮结构复杂、服役状态参差不一,故离心压缩机叶轮的再制造设计具有挑战性。国内已经有许多学者对叶轮再制造进行了研究,张洪潮等[2]通过模拟压缩机叶轮在通电瞬间的电流密度、温度场和应力场的分布,提出了阻止叶轮疲劳裂纹扩展的方法;舒林森等[3]针对再制造叶轮结构特征的三维建模问题,提出了叶轮结构特征重构方法,构建了再制造叶轮零部件服役寿命预测模型;许磊等[4]为了提高离心压缩机再制造叶轮仿真实验的仿真精度与求解效率,提出了一种基于拓扑的再制造叶轮六面体结构网格划分方法;刘慧杨[5]通过模拟不同工况下的叶轮,采集力学状态数据,分析了叶轮的工作转速和过盈量对其接触压力分布的影响规律;赵彦华等[6]提出一种使用FeCr合金粉料并通过激光熔覆技术在预置缺陷的KMN钢基体上制得修复层的方法;王浩等[7]对受损叶轮原始三维点云进行滤波和精简,重建了叶轮叶片的再制造目标模型。上述研究主要集中在再制造叶轮寿命预测模型的建立、网格划分和损伤修复方法等方面,总体仍存在以下问题:①对叶轮结构设计和服役性能的关系研究较少,亦未见将寿命预测模型用于叶轮的结构反馈优化设计;②传统的叶轮优化设计主要以性能为目标进行结构优化,兼及结构改变对叶轮寿命的影响,很少对叶轮寿命进行定量控制,从而导致叶轮的再制造时机出现提前或滞后现象,产生很大的资源浪费。
针对传统再制造模式所存在的问题,国内学者提出了主动再制造的理念。文献[8]探讨了主动再制造时间区域上限和下限的预判方法,为主动再制造时机点的选择提供了理论依据;文献[9]针对目前缺乏再制造可行性强度指标以及再制造设计反馈机制的不完善现象,提出强度冗余的概念,实现了基于强度冗余的零部件的主动再制造优化设计;文献[10]针对再制造毛坯中零件寿命的不确定因素,提出了零部件寿命匹配模式,建立了零部件设计信息与服役映射模型;文献[11]分析了额定转速下同尺寸非晶定子铁心替换对再制造电机空载、负载性能的影响,并对再制造电机中非晶合金定子铁心槽型尺寸及绕组结构进行了优化。但是关于离心压缩机叶轮的主动再制造设计的研究非常少。
本文以离心压缩机叶轮为例,基于主动再制造模式的理念,通过分析叶轮特征结构参数变化对其服役性能的影响,研究叶片特征结构(出口安放角、入口安放角和后缘厚度)与叶轮服役疲劳寿命之间的关系,运用CREO软件构建叶轮三维模型,结合ANSYS软件进行仿真验证,通过调整叶轮设计参数,确定较优的结构参数组合值,使叶轮主动再制造时间点处于定期维护时域中,从而实现离心压缩机叶轮的主动再制造设计和时机调控。
1 叶轮主动再制造设计
与传统再制造相比,主动再制造[12]具有主动性、时机最佳性、关键件优先性和可批量性等显著特征,而且产品在服役过程中存在一个可以进行再制造的使用时间区域,在此区域之前,产品不需要进行再制造;在此区域之后,在当前技术条件下,产品丧失再制造价值,这个时间区域为再制造时域,如图1所示。

图1 产品主动再制造时域Fig.1 Product predecisional remanufacturing time domain
图1中产品性能退化拐点(IP)与性能退化阈值点(TP)分别对应时间点TIP与TTP,产品的再制造时域R=[TIP,TTP]。产品处于再制造时域内时,适合再制造。当产品处于性能退化拐点附近区间2ΔT时,进行再制造,其经济性、环境性、技术性最佳,对应的时间区域(RP=[TIP-ΔT,TIP+ΔT])即主动再制造时域。
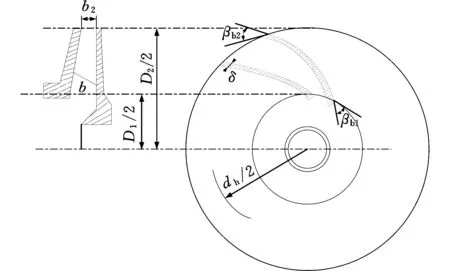
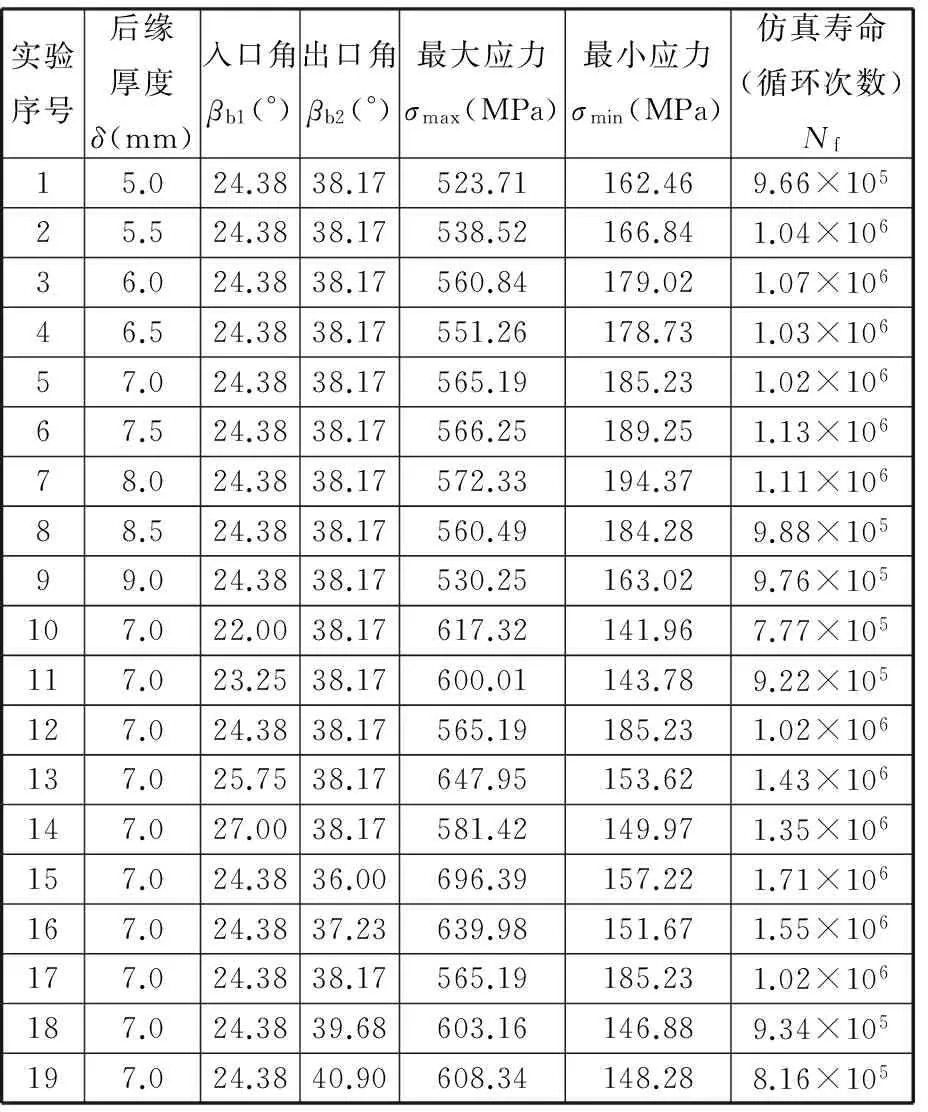
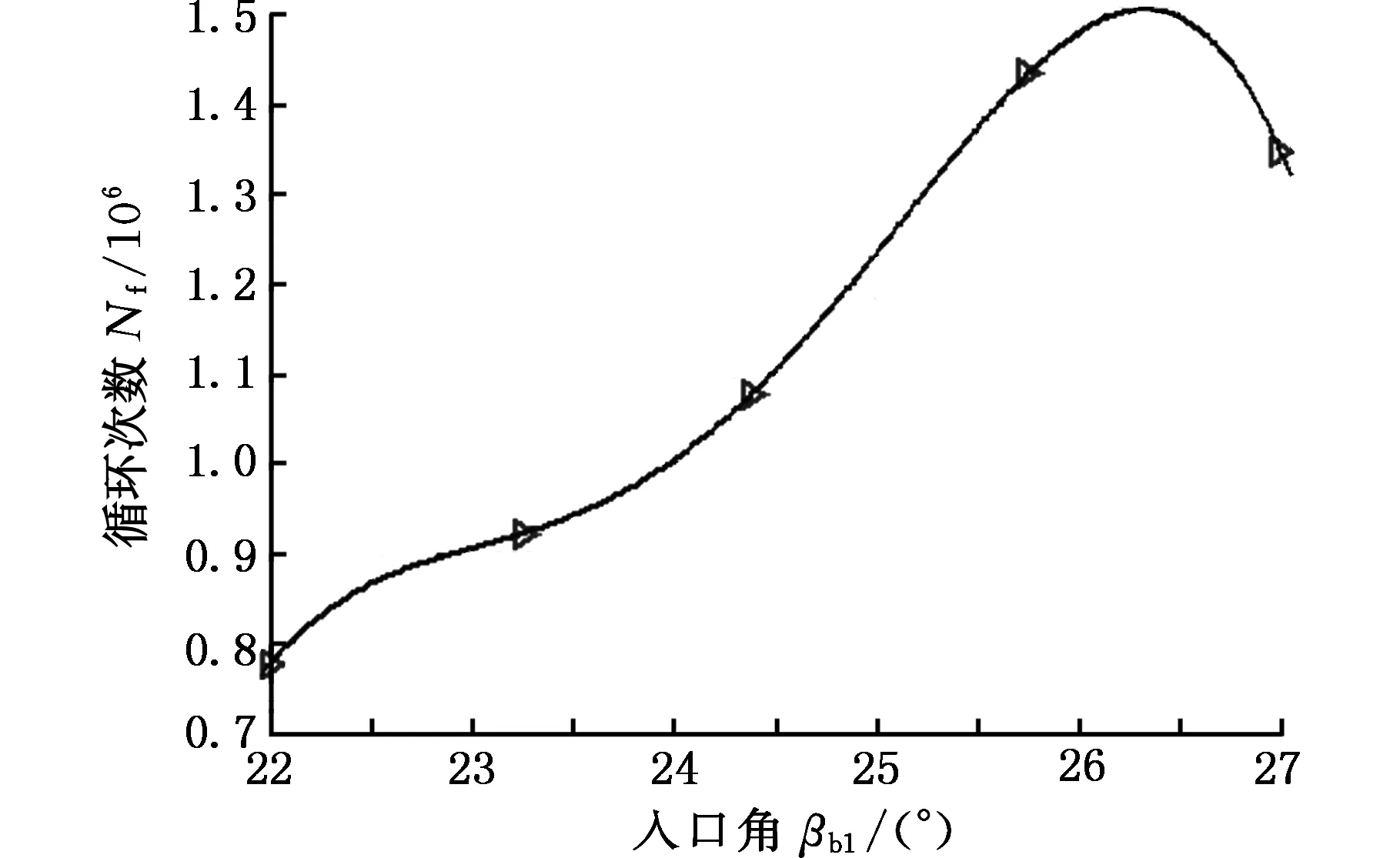
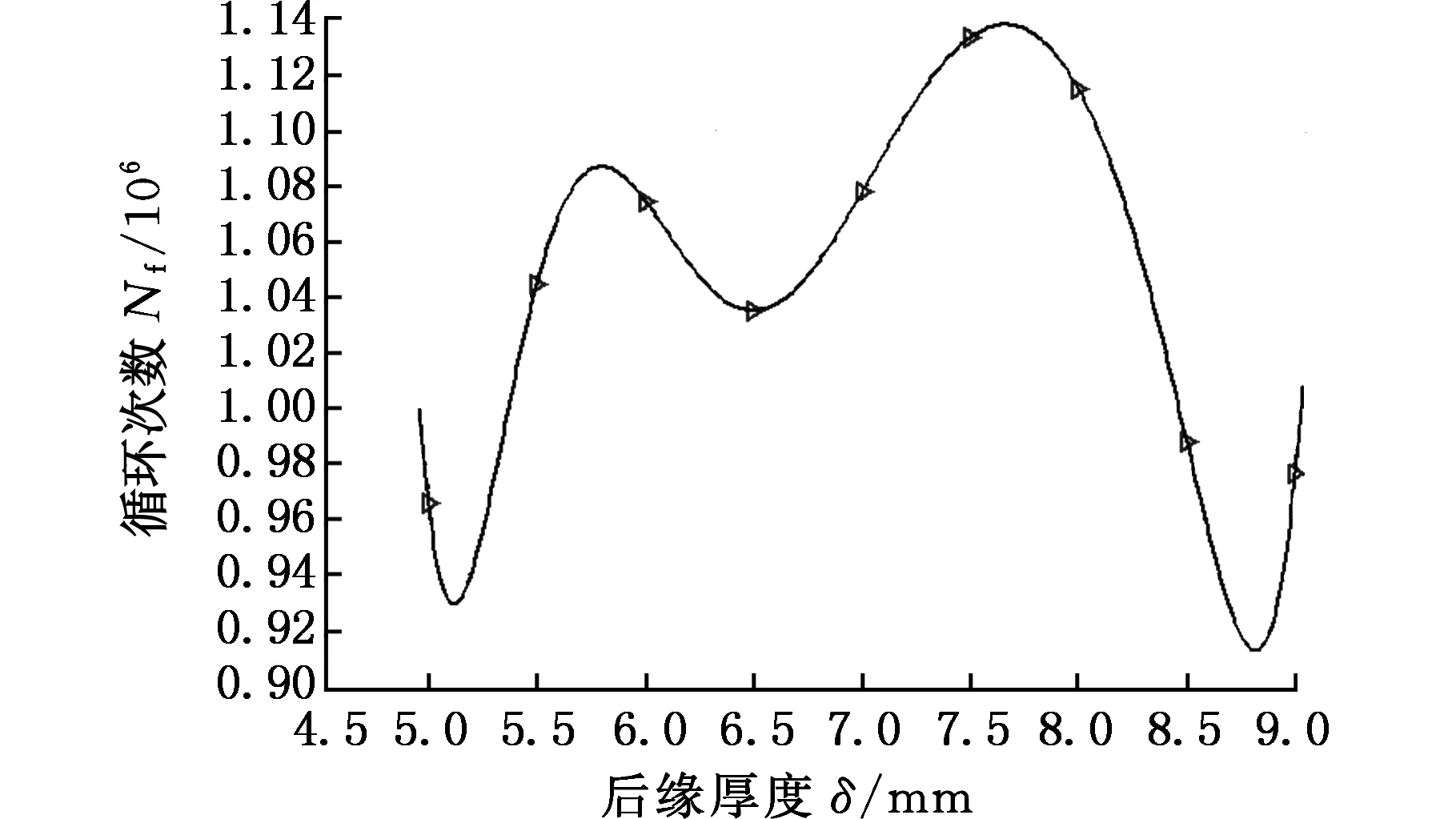
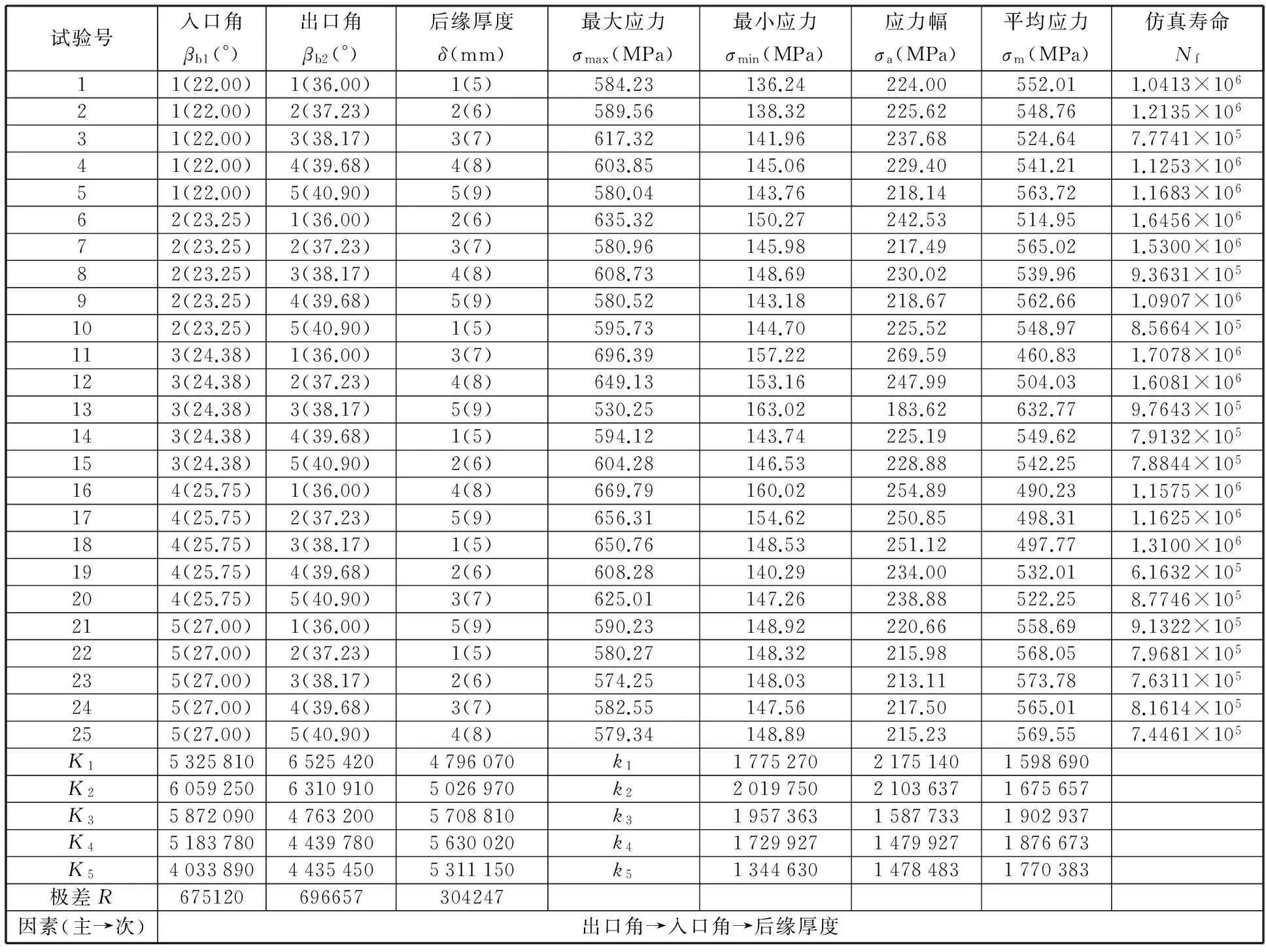
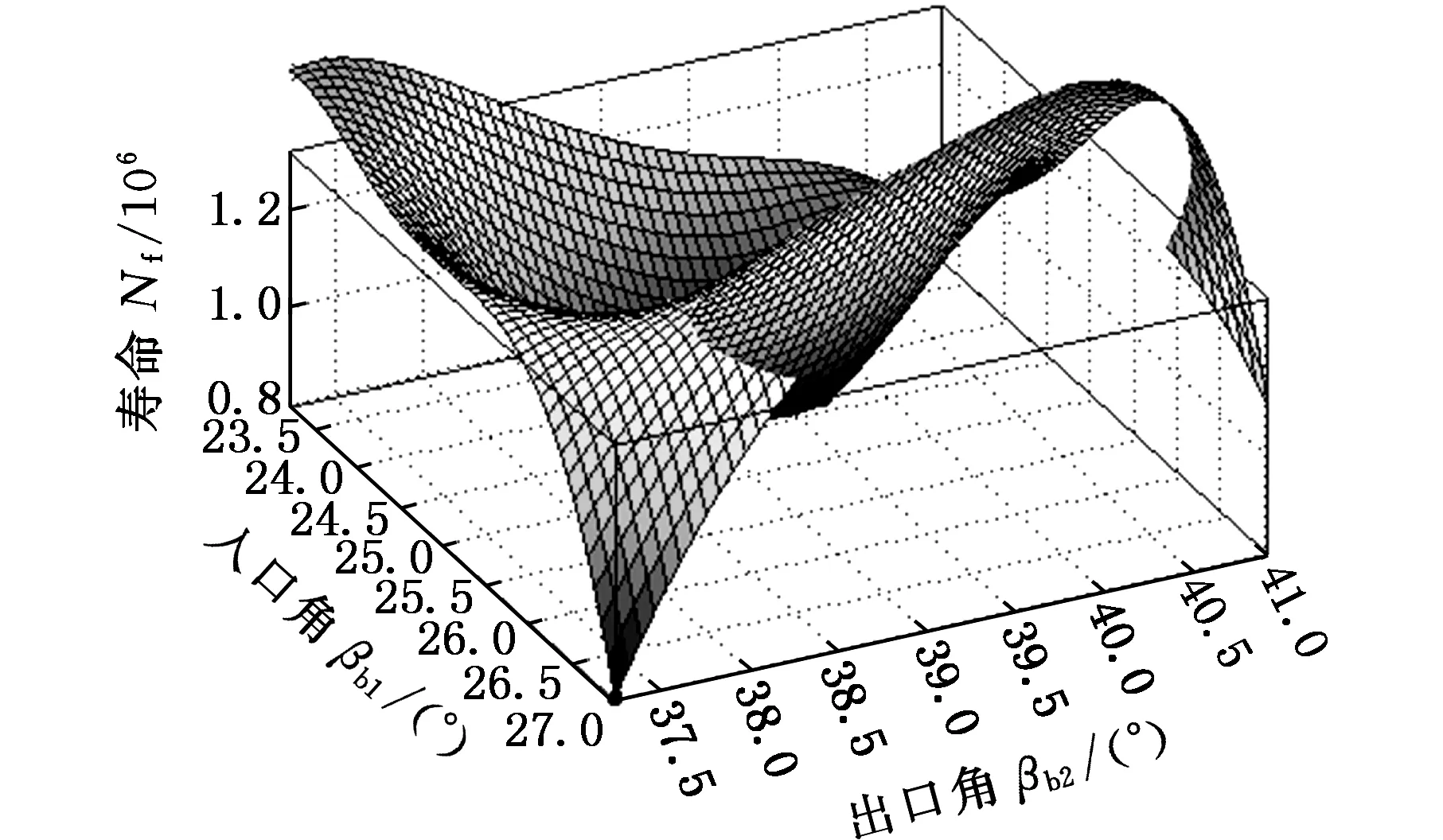
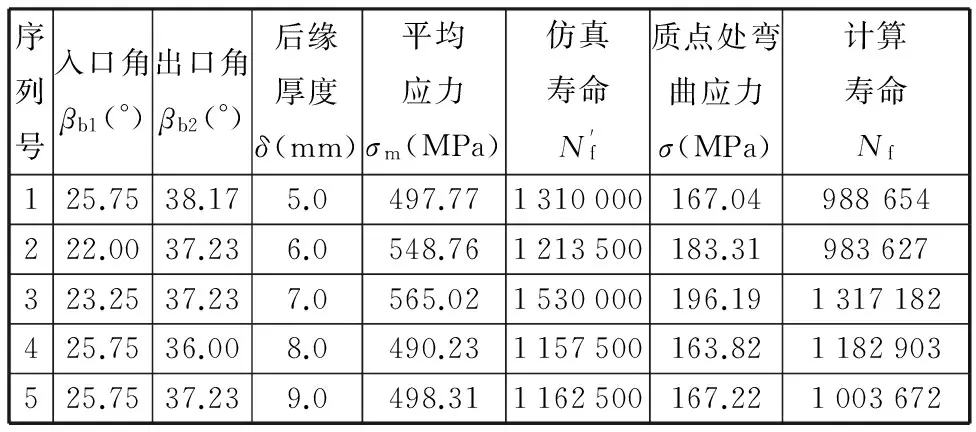
拐点的产品性能为PIP,阈值的产品性能为PTP,从TIP-ΔT点开始,产品的各项性能指标会随着使用时间的延长而急剧劣化,如果PU对应TIP-ΔT时刻的产品性能(包括产品服役能耗、使用及再制造成本等),PD对应TIP+ΔT时刻产品性能(包括产品服役能耗、使用及再制造成本等),则有TIP-ΔT 根据离心式压缩机设计手册[1],压缩机在服役过程中,叶轮等核心部件因为疲劳损伤导致性能下降,造成整机运行状态不安全,为避免产生严重后果,离心压缩机会在使用N年后进行一次停机维护。此时刻对压缩机叶轮进行再制造,又往往会因为叶轮的性能退化拐点并不是停机维护的时间点,远离主动再制造时域,导致叶轮因为过度使用而产生滞后再制造,或性能退化指标还没有达到再制造临界点而出现提前再制造。由此,针对叶轮的主动再制造设计,如果使叶轮的再制造临界点Tcr能够落在主动再制造时间区域[TIP-ΔT,TIP+ΔT]内,不仅可以省略检测判断叶轮能否再制造的步骤,直接对叶轮进行主动再制造,而且避免了叶轮的提前或滞后再制造,即N≈TIP,且0 在主动再制造设计中,再制造时机的选择与零部件结构设计相关联,因为设计参数改变,零件的应力分布、弯曲强度、扭转强度等也会随之变化,进而影响服役寿命。零件服役寿命和结构之间存在着映射关系,而且产品的服役时间主要取决于零部件的磨损和疲劳。对于离心压缩机,叶轮的疲劳损伤是主要因素[13],所以当进行压缩机叶轮主动再制造设计时,需要确定叶轮结构与疲劳寿命之间的关系。叶轮主动再制造设计和时机调控的主要过程(图2)如下:①根据设计手册、行业规范、统计分析、失效评估、客户需求等确定初始设计方案下压缩机综合性能退化拐点TIP;②选取叶轮特征结构,通过理论分析和仿真实验相结合的方法建立特征结构-寿命映射模型,确定叶轮再制造临界点Tcr,完成主动再制造设计;③匹配叶轮再制造临界点和压缩机主动再制造时机点,判断该叶轮再制造问题属于提前或者滞后再制造问题,并基于特征结构-寿命映射模型,通过优化结构设计参数,调控叶轮再制造临界点,使叶轮再制造临界点Tcr趋向压缩机主动再制造理想时间点TIP,从而完成叶轮再制造时机调控;④对调控后的叶轮优化设计方案进行效率分析,确定叶轮性能变化。 图2 叶轮主动再制造设计和时机调控过程Fig.2 Design and Timing control process for impeller Predecissional Remanufacturing 对于机械零件,零部件的再制造可行性是与设计参数、失效形式和服役特性相互关联的,需要选取关键结构来进行分析,为此引入特征结构的概念[9],将零件中承担特定功能或作用的结构定义为特征结构,而将其他结构规划为一般的辅助结构。辅助结构的设计只要满足功能要求即可,特征结构则对应于再制造,是需要重点进行参数优化的结构。离心压缩机叶轮的结构参数通常有:转速n,叶片出入口安放角βb2、βb1,叶片数Z,叶片出口相对宽度b2/D2(叶片出口宽度b2、叶轮出口直径D2),叶片后缘厚度δ,轮毂直径dh,叶片宽度b,叶轮入口直径D1,叶道宽度a等,结构参数标记如图3所示。 图3 叶轮结构平面简图Fig.3 Impeller structure plane diagram 由于离心力和气动力在叶轮叶片根部最易产生疲劳断裂,故叶片的疲劳破坏是叶轮失效的主要形式[13]。根据离心式叶轮设计理论,压缩机叶轮通常采用圆柱形叶片[14],在设计时,是通过先确定叶轮入口安放角βb1和出口安放角βb2,再绘制型线,从而得到圆弧形叶片每一处叶片安放角。本文以某压缩机企业PCL8L型叶轮为研究对象,该叶轮是闭式后弯叶片叶轮,即叶片弯曲方向与叶轮旋转方向相反,叶片前缘和后缘呈椭圆形状。由于气体从后缘流出通道面积扩大,在叶片尾部形成尾迹,会带来损失,叶轮尾缘的厚度改变会对压缩机的压比、气动性能及效率造成影响[13]。 综上所述,本文选择叶轮的入口安放角、出口安放角及叶片后缘厚度作为叶轮的特征结构来进行叶轮的主动再制造设计。 根据结构疲劳设计基本理论,对于平均应力为σm的非对称疲劳应力,疲劳寿命估计方程的Basquin修正方程为[15] (1) 对于离心压缩机后弯型圆弧叶片,其质点处的弯曲应力[17] (2) 式中,ρ为叶轮材料密度;ω为角速度;β为叶片质点处的安放角;叶轮入口半径R1=0.174 m,叶轮出口半径R2=0.360 m,叶轮圆弧所对应的中心角α=0.172 75π,叶片平均宽度b=0.0539 m,叶片质心到叶轮中心距离Rc=0.2538 m。 根据D’Alembert原理,在动平衡状态下,离心力可以看作一个外载荷,可以用质点平衡应力表示整个单元乃至整个零件的应力分布状况[18-19],因此,当用质点处弯曲应力σ来表示平均应力σm时,假设σm=kσ,k为表征零件不同结构的系数,并把式(2)代入式(1),则可得到基于叶片入口安放角、出口安放角和后缘厚度的特征结构-寿命映射模型: (3) 根据确定的数学模型,进行离心压缩机的仿真分析。本文以某企业PCL8L型叶轮为研究对象,叶轮材料采用马氏体不锈钢FV520B -I,弹性模量为210 GPa,泊松比为0.3,密度为7860 kg/m3,叶轮叶片数为15,工作转速为8500 r/min,工作介质为理想气体,质量流量qm为10.5 kg/s,进口压力为0.8 MPa,进口温度为20 ℃,出口压力为13 MPa,总压比约16。取叶轮初始设计参数入口角βb1=24.38°,出口角βb2=38.17°,叶片后缘厚度δ=7 mm,叶轮入口直径D=348 mm,叶轮出口直径D2=720 mm,叶片出口宽度b2=37.44 mm,根据文献[14],本文中离心压缩机叶轮为后向叶轮,入口安放角的取值范围为21.9830°<βb1<27.1573°,出口安放角的取值范围为35.7730°<βb2<40.9473°。应用CREO3.0软件建立叶轮模型和9种不同叶片后缘厚度(5.0 mm、5.5 mm、6.0 mm、6.5 mm、7.0 mm、7.5 mm、8.0 mm、8.5 mm、9.0 mm)的叶片模型,如图4、图5所示。同时调整叶片入口安放角为22.00°、23.25°、24.38°、25.75°、27.00°,出口安放角为36.00°、37.23°、38.17°、39.68°、40.90°,运用ANSYS进行仿真分析,根据单一特征结构的变化数量,进行19组实验,结果见表1,叶片出口安放角、入口安放角和后缘厚度的单一特征结构与叶轮寿命(循环次数)之间的关系曲线如图6~图8所示。 图4 叶轮模型Fig.4 Impeller model 图5 不同后缘厚度叶片模型Fig.5 Leaf model with different trailing edge thickness 实验序号后缘厚度δ(mm)入口角βb1(°)出口角βb2(°)最大应力σmax(MPa)最小应力σmin(MPa)仿真寿命(循环次数)Nf15.024.3838.17523.71162.469.66×10525.524.3838.17538.52166.841.04×10636.024.3838.17560.84179.021.07×10646.524.3838.17551.26178.731.03×10657.024.3838.17565.19185.231.02×10667.524.3838.17566.25189.251.13×10678.024.3838.17572.33194.371.11×10688.524.3838.17560.49184.289.88×10599.024.3838.17530.25163.029.76×105107.022.0038.17617.32141.967.77×105117.023.2538.17600.01143.789.22×105127.024.3838.17565.19185.231.02×106137.025.7538.17647.95153.621.43×106147.027.0038.17581.42149.971.35×106157.024.3836.00696.39157.221.71×106167.024.3837.23639.98151.671.55×106177.024.3838.17565.19185.231.02×106187.024.3839.68603.16146.889.34×105197.024.3840.90608.34148.288.16×105 图6 叶片入口角和叶轮寿命之间的关系Fig.6 Relationship between leaf inlet angle and impeller life 根据仿真结果,在其他变量一定时,叶轮寿命在规定的入口角范围内,寿命与入口角呈增函数关系;在规定的出口角范围内,寿命与出口角呈减函数关系;在规定后缘厚度范围内,寿命呈现先增大后减小的变化趋势。 图7 叶片出口角和叶轮寿命之间的关系Fig.7 Relationship between leaf outlet angle and impeller life 图8 叶片后缘厚度和叶轮寿命之间的关系Fig.8 Relationship between leaf trailing edge thickness and impeller life 在叶轮单一特征结构与寿命关系的基础上,分别取叶轮的入口角βb1为22.00°、23.25°、24.38°、25.75°、27.00°,出口角βb2为36.00°、37.23°、38.17°、39.68°、40.90°,叶片后缘厚度δ为5 mm、6 mm、7 mm、8 mm、9 mm进行正交试验,选择L25(56)正交表来进行仿真分析,结果见表2。同时通过MATLAB软件建立后缘厚度分别为5 mm、6 mm、7 mm、8 mm、9 mm时入口角、出口角和寿命关系的三维曲面模型,如图9所示。在进行ANSYS软件进行仿真分析的过程中,由仿真得出的最大应力σmax和最小应力σmin可以计算出应力幅σa: σa=Δσ/2=(σmax-σmin)/2 (4) 平均应力可用Goodman方程σa=σ-1(1-σm/σb)计算,其中σb=1030 MPa(σb为叶轮材料的断裂极限),σ-1=500 MPa(σ-1为叶轮材料对称循环疲劳强度),则平均应力 σm=(1-σa/σ-1)σb=1030(1-σa/500)(MPa) (5) 将计算出的应力幅σa代入式(5)即可求出平均应力σm。 表2 特征结构与寿命关系正交试验 (a)δ=5 mm (b)δ=6 mm (c) δ=7 mm (d) δ=8 mm (e) δ=9 mm图9 出口角、入口角和寿命关系三维曲面模型Fig.9 3D surface model for inlet angle, outlet angle and life relationship 对特征结构和寿命关系进行量化,采用响应曲面法对仿真结果进行最小二乘法拟合,确定二次多项式回归方程: (6) 对回归方程的系数进行显著性检验,特征因素βb1、βb2和δ都对寿命Nf的线性效应显著,δ2对寿命Nf的曲面效应最为显著,βb2δ对寿命Nf的交互影响最为显著。 分析正交试验以及三维曲面模型图的结果,可以得出:①出口安放角的变化对叶轮寿命的影响最大,其次为入口安放角,后缘厚度的变化对叶轮寿命的影响最小。根据文献[14],因为出口角βb2对压缩机叶轮级的能量头系数和效率影响最为显著,βb2越大,能量头系数越高,工作效率越低,而且入口角βb1越小,效率越低;另外,当叶片后缘厚度增大到合适的数值时,能显著地提高叶轮的结构强度,所以上述仿真结果符合理论分析。②固定叶片后缘厚度δ为5 mm、7 mm和8 mm时,寿命最大区域集中在βb1>23.25°,βb2<38.17°范围内,后缘厚度δ=6 mm时,寿命随着出口角和入口角的增大而增大;后缘厚度δ=9 mm时,寿命随着出口角和入口角的增大呈现凹函数变化趋势。 由上述对叶轮特征结构-寿命映射模型的仿真分析可知,当选取小出口角、大入口角并增大适当的后缘厚度时,叶轮疲劳寿命增加,从而为主动再制造时机调控提供参数优化设计方案。 叶轮主动再制造时机调控,是在确定压缩机主动再制造时间点的情况下,根据叶轮特征结构-寿命映射模型,优化叶轮特征结构出口角、入口角和后缘厚度的设计参数值,调控再制造临界点,并与压缩机主动再制造时机相匹配的过程。 因为压缩机的主动再制造时间点是5年,即1.1130×106次循环,代入式(3),借助MATLAB软件求解,并根据仿真分析确定每个厚度下的参数选择,见表3。 表3 特征结构参数值选取 根据式(2)求出每组参数对应的质点处弯曲应力,又已知平均应力,便可确定k值,再根据式(3)求出每组参数对应的计算寿命,选取与仿真寿命接近的一组,即βb1=25.75°、βb2=36°、δ=8 mm,此时叶轮循环次数为1.1575×106,寿命为Tcr2=5.19 a,满足Tcr2>N>TIP-ΔT,符合主动再制造设计要求。 调控叶轮再制造时机Tcr2=5.19 a后,须验证叶轮性能的变化。根据文献[14],流动损失占能量损失的绝大部分,对流体机械的工作效率起决定性的作用。针对本文的闭式后弯型叶轮,采用损失系数计算法确定叶轮效率变化。叶轮内总的流动损失 ΔPimp=ΔPr+ΔPb+ΔPdif= (7) 式中,ΔPr为轴向变径向的流动损失;ΔPb为叶道内的损失;Pdif为叶道内的扩散损失;ζr为弯道损失系数;ζb为叶道内的损失系数;ζdif为叶道内的扩散损失系数;ρ为流体的密度;w1、w2分别为叶道入口和出口前的相对速度。 根据压缩机设计理论[13],叶轮喉部流速 c0=qVn/(πD1b) (8) 式中,qVn为叶道内流量。 叶道入口后的相对速度 (9) 叶道出口前的相对速度 (10) 选取ζr=0.15,ζb=0.15,ζdif=0.15,ρ=1.2 kg/m3,qVn=1.76 m3/s。代入参数值βb1=24.38°、βb2=38.17°、δ=7 mm,可以由式(7)计算出初始设计参数下叶轮的流动损失为150.23 Pa,再代入参数值βb1=25.75°、βb2=36°、δ=8 mm,则可算出优化设计参数下叶轮的流动损失为137.65 Pa,说明参数优化后的叶轮流动损失降低,效率提升。 综上所述,通过优化叶轮特征结构设计参数值为βb1=25.75°、βb2=36°、δ=8 mm,延长叶轮服役寿命,使叶轮的再制造临界点延后,并落于压缩机主动再制造时域中,不仅使叶轮的性能得到优化提升,而且避免了初始设计方案下叶轮的过度使用。 (1)研究叶轮特征结构与疲劳寿命之间的量化关系,构建了特征结构-寿命映射模型,并将服役映射模型应用在叶轮主动再制造的结构反馈优化设计中,由于考虑材料的本身特性和零件结构对质点处弯曲应力分布以及寿命的影响,故基于映射模型进行的主动再制造设计更加符合叶轮服役的实际情况。 (2)阐述了借助特征结构-寿命映射模型对关键零部件进行主动再制造时机调控的过程,综合考虑产品-关键零部件-结构之间的联系,以PCL8L型叶轮为例,调控叶轮的再制造临界点为5.19年,实现了对叶轮寿命的定量控制,并且结构参数优化后的叶轮最大应力为669.79 MPa,小于材料屈服极限,符合设计强度要求,从而验证了主动再制造设计和时机调控方法的可行性,为目前零部件提前或者滞后再制造问题提供了新的解决途径。 (3) 本设计方法对于不同的产品及零部件可以具体分析,具有普适性。但是叶轮特征结构与寿命映射模型的模拟结果只能应用于离心式压缩机,对于其他机械,仍需建立一个新的服役映射模型,而且应分析零件结构之间的交互作用以及装配应力影响等,随着对主动再制造研究的深入,将逐步进行完善。 [1] 郁永章, 姜培正, 孙嗣莹,等. 压缩机工程手册[M]. 北京: 中国石化出版社,2012. YU Yongzhang, JIANG Peizheng, SUN Siying, et al. Compressor Engineering Handbook[J]. Beijing:China Petrochemical Press,2012. [2] 张洪潮, 于静, 郝胜智, 等. 电磁场的热效应在再制造毛坯裂纹止裂中的应用[J]. 机械工程学报,2013,49(7):21-28. ZHANG Hongchao, YU Jing, HAO Shengzhi, et al. Application of Electro-magnetic Heat Effect on Arresting the Crack in Remanufacture Blank[J].Journal of Mechanical Engineering,2013,49(7):21-28. [3] 舒林森, 曹华军, 许磊. 离心压缩机再制造叶轮结构特征三维建模方法及应用[J]. 机械工程学报,2014,50(3):184-190. SHU Linsen, CAO Huajun, XU Lei. 3D Characteristic Modeling Method and Application for Remanufacturing Impeller of Centrifugal Compressor[J]. Journal of Mechanical Engineering,2014,50(3):184-190. [4] 许磊, 曹华军, 舒林森,等. 基于拓扑的再制造叶轮全六面体网格生成方法[J]. 计算机集成制造系统,2014,20(11):2712-2718. XU Lei, CAO Huajun, SHU Linsen, et al. Hexahedral Meshes Generation Method for Remanufactured Impeller Based on Topology[J].Computer Integrated Manufacturing System,2014,20(11):2712-2718. [5] 刘慧杨.叶轮再制造临界阀值界定中服役环境及疲劳裂纹扩展分析研究[D].大连:大连理工大学,2014. LIU Huiyang. The Analysis of Service Environment and Fatigue Crack Growth in Determination of Critical Threshold of Impeller Remanufacturing[J].Dalian: Dalian University of Technology,2014. [6] 赵彦华, 孙杰, 李剑锋,等. KMN钢激光熔覆FeCr合金修复层组织性能及耐磨、耐蚀性研究[J]. 机械工程学报,2015,51(8):37-43. ZHAO Yanhua, SUN Jie, LI Jianfeng, et al. Research on Microstructure Properties and Wear and Corrosion Resistance of FeCr Repaired Coating on KMN Steel by Laser Cladding[J]. Journal of Mechanical Engineering,2015,51(8):37-43. [7] 王浩, 赵世伟, 王立文, 等. 离心压缩机受损叶轮再制造方法[J]. 农业机械学报, 2016,47(5):407-412. WANG Hao, ZHAO Shiwei, WANG Liwen, et al. Remanufacture Method of Damaged Impeller in Centrifugal Compressor[J].Transactions of the Chinese Society for Agricultural Machinery,2016,47(5):407-412. [8] 刘光复, 刘涛,柯庆镝,等. 基于博弈论及神经网络的主动再制造时间区域抉择方法研究[J]. 机械工程学报,2013,49(7):29-35. LIU Guangfu, LIU Tao, KE Qingdi, et al. Time Interval Decision-making Methods for Active Remanufacturing Product Based on Game Theory and Neural Network[J]. Journal of Mechanical Engineering,2013,49(7):29-35. [9] 宋守许, 刘明, 柯庆镝,等. 基于强度冗余的零部件再制造优化设计方法[J]. 机械工程学报,2013,49(9):121-127. SONG Shouxu, LIU Ming, KE Qingdi, et al. Components Optimization Design for Remanufacturing Based on Residual Strength[J]. Journal of Mechanical Engineering,2013,49(9):121-127. [10] 宋守许, 冯艳, 柯庆镝,等. 基于寿命匹配的零部件再制造优化设计方法[J].中国机械工程,2015,26(10):1323-1329. SONG Shouxu, FENG Yan, KE Qingdi, et al. Components Optimization Design for Remanufacturing Based on Life Matching[J]. Journal of Mechanical Engineering,2015,26(10):1323-1329. [11] 宋守许, 谭浩, 王战春, 等. 非晶合金定子铁心对再制造电机性能的影响[J]. 中国机械工程, 2016,27(16):2179-2185. SONG Shouxu, TAN Hao, WANG Zhanchun, et al. Effects of Amorphous Stator on Performance of Remanufacturing Motor[J].China Mechanical Engineering,2016,27(16):2179-2185. [12] 刘涛. 主动再制造时间区域抉择及调控方法研究[D]. 合肥: 合肥工业大学,2014. LIU Tao. Research on Time Interval Decision-making and Control Methods for Active Remanufacturing[D].Hefei: Hefei University of Technology,2014. [13] SIVAPRASAD S,NARASAIAH N,DAS S K,et al. Investigation on the Failure of Air Compressor[J]. Engineering Failure Analysis,2010,17(1):150-157. [14] CHEN Xinde. Vane Type Pump, Fan, Compressor (Principle, Design, Operation, Strength)[M]. Beijing:China Machine Press,2011. [15] VYAS N S, SIDHARTH, RAO J S. et al. Dynamic Stress Analysis and a Fracture Mechanics Approach to Life Prediction of Turbine Blades [J]. Mech. Math. Theory,1997,32(4):511-527. [16] 吴承伟, 关振群, 郭杏林,等. 大型离心压缩机叶轮叶片疲劳可靠性分析[J]. 装备制造技术,2008,8:1-3. WU Chenwei, GUAN Zhenqun, GUO Xinglin, et al. Fatigue Reliability Analysis of Blades of Large Centrifugal Compressor[J].Equipment Manufacturing Technology,2008,26:1-3. [17] SONG Shouxu, TAI Yingying, KE Qingdi. Establishment and Application of the Service Mapping Model for Proactive Remanufacturing Impeller[J].Journal of Central South University,2016,23(12):3143-3152. [18] 蔡兆麟, 韩海燕, 彭鑫. 旋转叶轮三维应力分布及其改善措施[J]. 华中科技大学学报(自然科学版),2003,31(12):81-83. CAI Zhaolin, HAN Haiyan, PENG Xin. 3D Stress Distribution of Ratate Impeller and Its Improvement[J]. Huazhong University of Science and Technology(Nature Science Edition),2003,31(12):81-83. [19] 韩文坝, 蔡冰清, 韩晓东. 质点平衡应力的概念[EB/OL].(2006-09-04)[2006-09-25] 中国科技论文在线, http://www.paper.edu.cn/html/releasepaper/2006/09/25/. HAN Wenba, CAI Shuiqing, HAN Xiaodong. The Concept of Particle Equilibrium Stress[EB/OL]. (2006-09-04)[2006-09-25]Chinese Scientific Papers Online,http://www.paper.edu.cn/html/releasepaper/2006/09/25/. [20] GUO Lijie. Study on Risk-based Intelligent Maintenance Decision-making for Petrochemical Rotating Machinery[D]. Beijing:Beijing University of Chemical Technology,2009. (编辑 陈 勇) Design and Timing Control for Centrifugal Compressor Impeller Predecissional Remanufacturing SONG Shouxu BU Jian KE Qingdi School of Mechanical Engineering, Hefei University of Technology, Hefei, 230009 Aimed at the present situations of remanufacturing components that often occured the issues of ‘lag of remanufacturing’ or ‘remanufacturing in advance’, a design method of predecisional remanufacturing and timing control for centrifugal compressor impellers was presented herein. By choosing vital component characteristic structures, combined with the theory of fatigue life and basic design method of impellers, the structure and performance of the service mapping model was established, the predecisional remanufacturing design of vital components was implemented. Through the optimization of structure parameters, changing the service performances and remanufacturing points of components, and matching with product performance degradation inflection points, the predecisional remanufacturing timing control was implemented. Taking the PCL8L type of centrifugal compressor impeller as an example, three structure characteristis of impellers(outlet angle, entrance angle and the trailing edge thickness)were selected, the quantitative relationship among the impeller structure characteristics and the service fatigue lifes was built. Then, through the simulation analysis and considering the current preventive maintenance requirements, the predecisional remanufacturing of timing control for centrifugal compressors. predecisional remanufacturing; centrifugal compressor; characteristics of structure; timing control 2016-09-19 国家重点基础研究发展计划(973计划)资助项目(2011CB013406);国家自然科学基金资助项目(51375133) TH122 10.3969/j.issn.1004-132X.2017.15.015 宋守许,男,1964年生。合肥工业大学机械工程学院教授、博士研究生导师。主要研究方向为绿色设计与绿色制造、再制造工程、产品资源化。E-mail:shouxus@163.com。卜 建(通信作者),男,1991年生。合肥工业大学机械工程学院硕士研究生。柯庆镝,男,1984年生。合肥工业大学机械工程学院副教授、博士。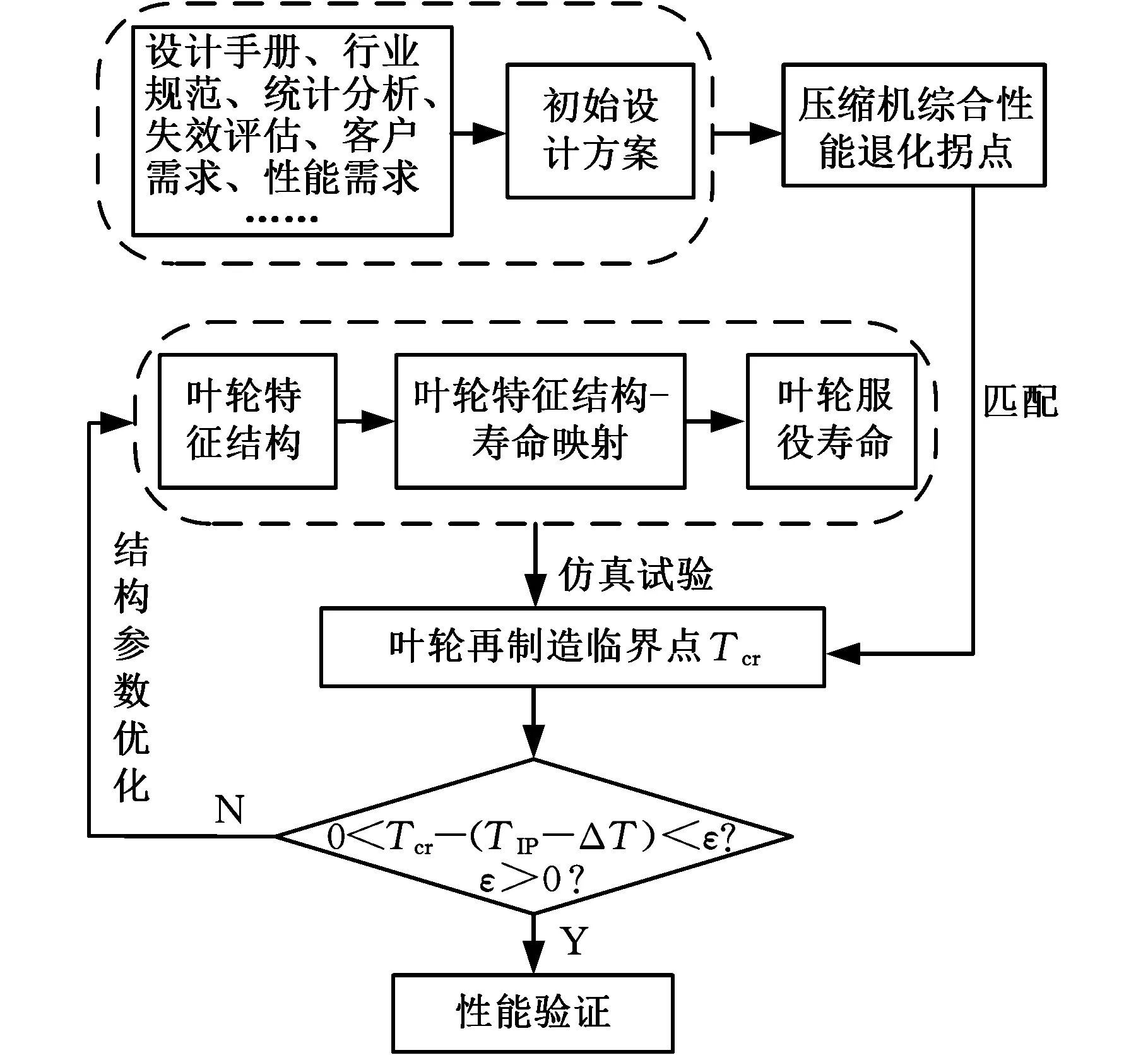
2 叶轮特征结构-寿命映射模型的确定
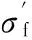
3 特征结构-寿命映射模型仿真分析





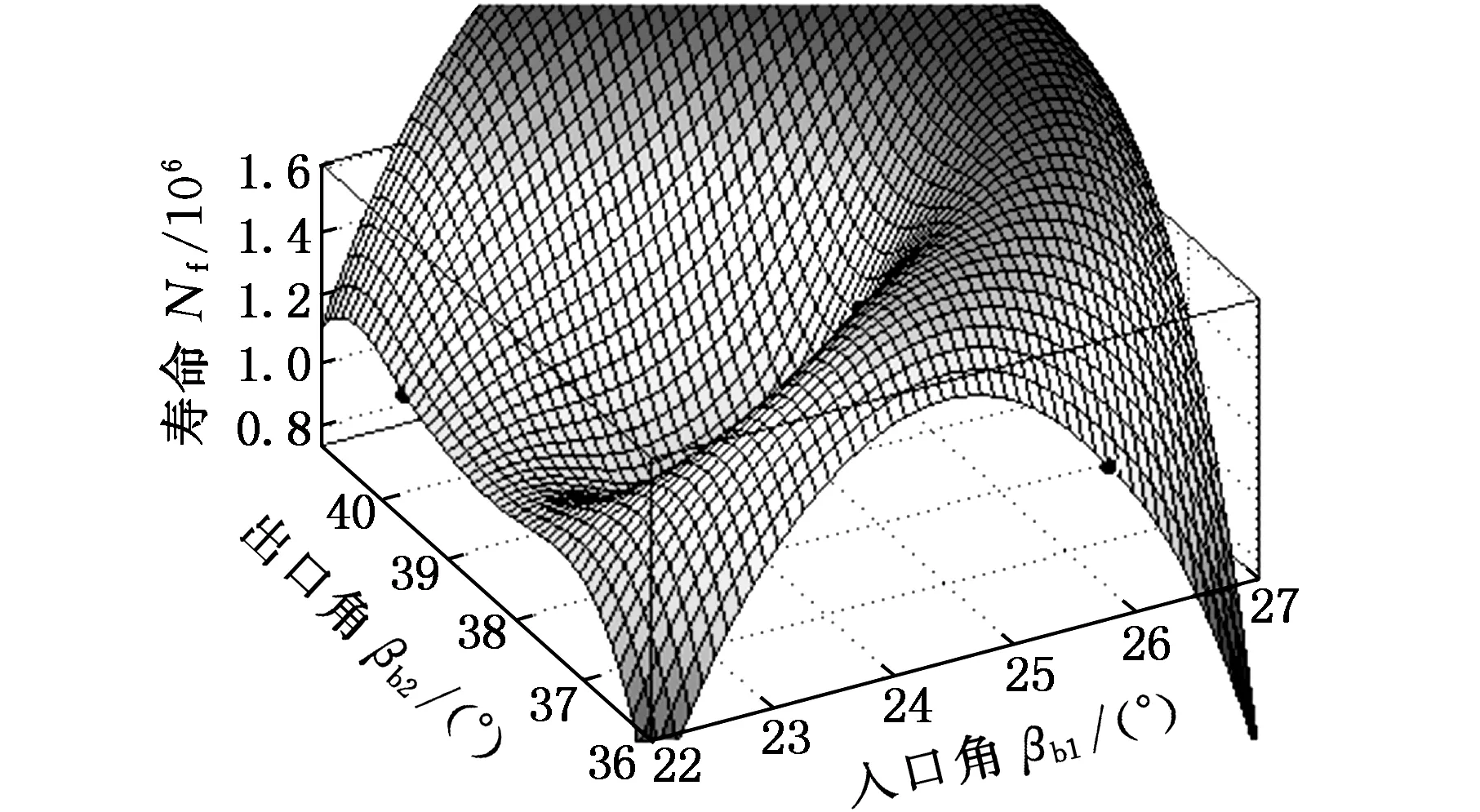
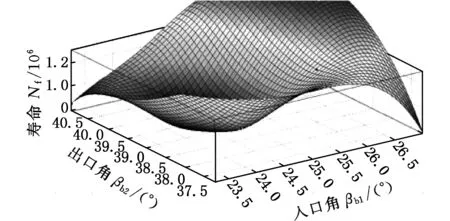
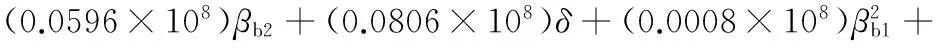
4 叶轮主动再制造时机调控
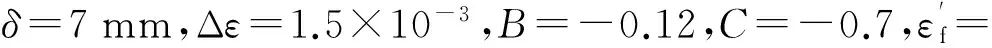
5 结论

